Capítulo 3 Probabilidade
Muito há para se falar sobre probabilidade desde a troca de correspondências entre Pascal e Fermat em 1654. Segundo Pierre-Simon Laplace16, ‘a teoria das probabilidades é, basicamente, o senso comum reduzido ao cálculo.’ Para o matemático italiano Bruno de Finetti17, ‘PROBABILIDADE NÃO EXISTE.’ Neste material serão utilizadas as noções axiomática, subjetiva e frequentista de probabilidade, descritas em detalhes na Seção 2.2 de (Press 2003).
\(\\\)
\(\\\)
3.1 Teoria dos Conjuntos
Um conjunto é uma coleção de elementos, sem repetição e não ordenada. Um subconjunto é uma coleção de elementos que pertencem a um determinado conjunto. Formalmente não existe definição para conjunto, subconjunto, elemento e pertinência, pois estas são consideradas noções primitivas (Iezzi and Murakami 1977).
3.1.1 Relações
Seja \(A\) um conjunto e \(a\) um elemento de \(A\). \(a \in A\) simboliza que \(a\) pertence ao conjunto \(A\). Se um elemento \(b\) não pertence ao conjunto \(A\), anota-se \(b \notin A\). Diz-se que um conjunto \(A\) está contido em outro conjunto \(B\) se todos os elementos pertencentes ao conjunto \(A\) também estiverem contidos em \(B\), simbolizado pelas relações \(A \subset B\) ou \(B \supset A\). Estas relações também podem ser lidas como \(A\) é subconjunto de \(B\).
| Conjunto-conjunto | Elemento-conjunto |
|---|---|
| \(T_{\male} \subset T\) | \(Aaron \in T\) |
| \(T_{\female} \subset T\) | \(Aaron \in T_{\male}\) |
| \(T \not\subset T_{\male}\) | \(Aaron \notin T_{\female}\) |
| \(T \not\subset T_{\female}\) | \(Fabiane \in T\) |
| \(T_{\female} \not\subset T_{\male}\) | \(Fabiane \notin T_{\male}\) |
| \(T_{\male} \not\subset T_{\female}\) | \(Fabiane \in T_{\female}\) |
3.1.2 Conjunto Vazio
Conjunto vazio18 é um conjunto sem elementos. Sua definição pode parecer um pouco estranha em um primeiro momento, mas é de grande importância na Teoria de Conjuntos. Intuitivamente pode-se pensar que alguns resultados são impossíveis em certos experimentos, gerando a necessidade prática de tal definição. Usualmente indica o resultado de uma operação de intersecção (Seção 3.1.3.2) onde não há elementos em comum entre os conjuntos considerados. É denotado por \(\lbrace \rbrace\) ou \(\emptyset\), e não deve ser confundido com a letra grega \(\phi\). Por definição o conjunto vazio é subconjunto de qualquer conjunto.
3.1.3 Operações
As operações com conjuntos são fundamentais na Teoria da Probabilidade. Deve-se diferenciar operações entre conjuntos e operações entre números. União (\(\cup\)), intersecção (\(\cap\)), complementar (\(A^c\)) e diferença (\(B-A\)) são operações entre conjuntos. Adição (\(+\)), subtração (\(-\)) e multiplicação (\(\times\)) são operações realizadas com números. As operações com conjuntos possuem associação com as operações numéricas, detalhadas a seguir. A forma usual para representação das operações entre conjuntos é utilizando o diagrama de Venn19.
3.1.3.1 União \(\cup\)
A operação de união é representada pelo símbolo \(\cup\). Indica que o novo conjunto gerado deve considerar todos os elementos dos conjuntos envolvidos na operação de união. Caso existam elementos iguais, eles não devem ser repetidos. Equivale em Português à palavra ‘ou’ e em Matemática à operação numérica de adição (\(+\)).
\[ T_{\female} \cup T = T. \]
3.1.3.2 Intersecção \(\cap\)
A operação intersecção é representada pelo símbolo \(\cap\). Indica que o novo conjunto gerado deve considerar apenas os elementos que sejam comuns aos conjuntos envolvidos na operação de intersecção. Equivale em Português à palavra ‘e’ e em Matemática à operação numérica de multiplicação (\(\times\)).
\[ T_{\female} \cap T = T_{\female}. \]
3.1.3.3 Complementar \(A^c\)
O complementar do conjunto \(A\) é representado por \(A^c\) e indica que o novo conjunto gerado deve considerar os elementos que não pertencem a \(A\), também chamados de não \(A\) ou \(\neg A\). É representado pelas simbologias \(A^c\) e \(\bar{A}\). Neste texto será adotada a notação \(A^c\) para não colidir com a notação de média amostral, também anotada pelo símbolo de barra \(\bar{A}\). Equivale em Português à palavra ‘não.’
3.1.3.4 Diferença \(B-A\)
A diferença entre os conjuntos \(B\) e \(A\) é denotada por \(B-A\) e pode ser lida como ‘os elementos que estão em \(B\) mas não estão em \(A\).’ Corresponde à operação numérica de subtração (\(-\)).
3.1.4 Cardinal e Conjunto das Partes/Potência
O cardinal de um conjunto indica seu número de elementos. O cardinal do conjunto \(A\) é denotado por \(|A|\), onde \(|A| \in \mathbb{N}\). O conjunto das partes ou conjunto potência de um conjunto \(A\) é o conjunto contendo todos os subconjuntos de \(A\), denotado por \(P(A)\). Por definição o conjunto vazio \(\emptyset\) é subconjunto de \(P(A)\). O cardinal do conjunto das partes é dado por \(|P(A)| = 2^{|A|}\).
A <- c(-9,0,5)
length(A)## [1] 3(ps <- rje::powerSet(A))## [[1]]
## numeric(0)
##
## [[2]]
## [1] -9
##
## [[3]]
## [1] 0
##
## [[4]]
## [1] -9 0
##
## [[5]]
## [1] 5
##
## [[6]]
## [1] -9 5
##
## [[7]]
## [1] 0 5
##
## [[8]]
## [1] -9 0 5length(ps)## [1] 83.1.4.1 Conjuntos Disjuntos e Partição
Conjuntos disjuntos são aqueles cuja intersecção é o conjunto vazio, ou seja, não se sobrepõem. Uma partição é uma quebra de um conjunto em subconjuntos disjuntos que estejam definidos em todo o espaço.
3.2 Definições
3.2.1 Experimento Aleatório
Um experimento aleatório é um processo no qual não se conhece o específico resultado antes de realizar o experimento, mas se conhece o conjunto dos possíveis resultados (espaço amostral). Um experimento aleatório pode ser medir alturas de pessoas, contar o dinheiro que entra por dia em um supermercado ou simplesmente lançar um dado. É considerado aleatório pois se desconhece o específico resultado em cada realização, ainda que sejam conhecidos todos os possíveis resultados.
3.2.2 Espaço Amostral
O espaço amostral é o conjunto de todos os possíveis resultados de um experimento aleatório, simbolizado por \(\Omega\).
3.2.3 Evento
Um evento é um subconjunto do espaço amostral.
\(\\\)
3.2.4 Probabilidade
Atribui-se a probabilidade do evento \(A\) como
\[\begin{equation} Pr(A)=\frac{m}{n} \tag{3.1} \end{equation}\]
onde
- \(m\) é o número de casos favoráveis para o evento \(A\)
- \(n\) é o número total de casos
A probabilidade frequentista é o limite da Equação (3.1) quando \(n \rightarrow \infty\).
Exemplo 3.16 (Cálculo de probabilidade) Suponha que um dado seja lançado 150 vezes, e observa-se a distribuição dos lançamentos apresentada na tabela a seguir.
| Face | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | Total |
|---|---|---|---|---|---|---|---|
| Frequência | \(18\) | \(24\) | \(34\) | \(26\) | \(27\) | \(21\) | \(150\) |
m <- c(18,24,34,26,27,21)
n <- sum(m)
(p2 <- m[2]/n)## [1] 0.16(ppar <- sum(m[c(2,4,6)])/n)## [1] 0.473(pimpar <- 1-ppar)## [1] 0.527MASS::fractions(ppar)## [1] 71/150MASS::fractions(pimpar)## [1] 79/1503.3 Propriedades
3.3.1 Propriedades fundamentais (Axiomas de Kolmogorov)
Um leitor mais atento pode perceber que foi feita uma combinação entre os axiomas de Kolmolgorov e as propriedades que são consequências destes axiomas. Tal abordagem tem por finalidade simplificar o entendimento neste curso de nível introdutório. Para maiores detalhes, recomenda-se (Feller 1968) e (James 2010).
- P1
\[\begin{equation} 0 \le Pr(A) \le 1 \tag{3.2} \end{equation}\] - P2
\[\begin{equation} Pr(\Omega)=1 \tag{3.3} \end{equation}\] - P3 Se \(A_1\), \(A_2\), …, \(A_k\) são conjuntos disjuntos, então \[\begin{equation} Pr(A_1 \cup A_2 \cup \ldots \cup A_k) = Pr(A_1) + Pr(A_2) + \ldots + Pr(A_k) \tag{3.4} \end{equation}\]
3.3.2 Propriedades secundárias
Das propriedades fundamentais resultam outras, apresentadas sem demonstração:
P4 (Complementar)
\[\begin{equation} Pr(A)=1-Pr(A^c) \tag{3.5} \end{equation}\]P5
\[\begin{equation} Pr(\emptyset)=0 \tag{3.6} \end{equation}\]P6
Se \(A_1\) e \(A_2\) são dois conjuntos quaisquer, então \[\begin{equation} Pr(A \cup B) = Pr(A) + Pr(B) - Pr(A \cap B) \tag{3.7} \end{equation}\]P7
\[\begin{equation} Pr(\left[ A \cup B \right]^c) = Pr(A^c \cap B^c) \tag{3.8} \end{equation}\]P8
\[\begin{equation} Pr(\left[ A \cap B \right]^c) = Pr(A^c \cup B^c) \tag{3.9} \end{equation}\]
aniv = function(n){
p = 1
for(i in 1:n){
p = p*(365-i+1)/365
}
return(1-p)
}
aniv(23)## [1] 0.507prob = sapply(1:100, aniv)
plot(1:100, prob, main = 'Pr(A)', xlab = '')
points(c(23, 57), c(aniv(23), aniv(57)), pch = 16, col = 'red')
legend(19, 0.55, '(23, 0.5073)', bty = 'n')
legend(51, 0.99, '(57, 0.9901)', bty = 'n')
# abline(v = c(23, 57), col = 'blue')
# abline(h = c(aniv(23), aniv(57)), col = 'blue')a. Explique em palavras a Eq. (3.10).
b. Mostre que a Equação (3.10) pode ser escrita como \[\begin{equation} Pr(A^c) = \left( 1 - \frac{1}{365} \right) \left(1- \frac{2}{365} \right) \cdots \left( 1- \frac{n-1}{365} \right) \tag{3.12} \end{equation}\] c. Escreva a função
aniv2 implementando a Eq. (3.12) e compare com aniv.\(\\\)
3.4 Probabilidade Condicional
Probabilidade condicional é a probabilidade do evento \(A\) após observada a ocorrência de um evento \(B\). A probabilidade de \(A\) dado \(B\) é
\[\begin{equation} Pr(A|B) = \dfrac{Pr(A \cap B)}{Pr(B)}, \; \; Pr(B) \ne 0 \tag{3.13} \end{equation}\]
Analogamente \[\begin{equation} Pr(B|A) = \dfrac{Pr(A \cap B)}{Pr(A)}, \; \; Pr(A) \ne 0 \tag{3.14} \end{equation}\]
As Equações (3.13) e (3.14) resultam na regra do produto, ou a probabilidade do evento intersecção:
\[\begin{equation} Pr(A \cap B) = Pr(A) \cdot Pr(B|A) = Pr(B) \cdot Pr(A|B) \tag{3.15} \end{equation}\]
Para três eventos: \[\begin{equation} Pr(A \cap B \cap C) = Pr(A) \cdot Pr(B|A) \cdot Pr(C|A \cap B) \tag{3.16} \end{equation}\]
De forma generalizada: \[\begin{equation} Pr(\cap_{i=1}^k A_i) = Pr(A_1) \cdot Pr(A_2|A_1) \cdot Pr(A_3|A_1 \cap A_2) \cdots Pr(A_k|A_1 \cap \cdots \cap A_{k-1}) \tag{3.17} \end{equation}\]
Quando ocorre \[\begin{equation} Pr(A|B) = \dfrac{Pr(A) \cdot Pr(B)}{Pr(B)} = Pr(A) \end{equation}\] é dito que \(A\) e \(B\) são independentes (\(A \ci B\)), uma vez que a observação de \(B\) não altera a opinião sobre \(A\). Os eventos são independentes dois a dois se \(A \ci B\), então \(A \ci B^c\), \(A^c \ci B\) e \(A^c \ci B^c\). As propriedades de probabilidade continuam valendo, permitindo que façamos
\[\begin{equation} Pr(A|B) = 1 - Pr(A^{c}|B) \tag{3.18} \end{equation}\] e \[\begin{equation} \frac{Pr(A \cap B|C)}{Pr(B|C)} = Pr(A|B \cap C) \tag{3.19} \end{equation}\]
Exercício 3.3 Refaça o Exemplo 3.18 considerando a informação \(C\): ‘a face é ímpar.’ Calcule:
- \(Pr(C)\)
- \(Pr(A \cap C)\)
- \(Pr(A \mid C)\)
- \(Pr(A^c \mid C)\)
3.5 Teorema da Probabilidade Total e o Teorema de Bayes

Considere uma partição conforme digrama de Venn da figura acima, onde \(A_1, \ldots, A_5\) formam uma distribuição de probabilidade, i.e., \(\sum_{i=1}^{5} Pr(A_i) =1\). Pode-se decompor \(B\) da seguinte forma:
\[\begin{equation}
B = \cup_{i=1}^{5} (A_i \cap B)
\end{equation}\]
Teorema 3.1 (Teorema da Probabilidade Total) Seja uma sequência enumerável de eventos aleatórios \(A_{1}, A_{2}, \ldots, A_{k}\), formando uma partição de \(\Omega\). Como as intersecções \(A_i \cap B\) são mutuamente excludentes, então de (3.4)
\[\begin{equation} Pr(B) = \sum_{i=1}^k Pr(A_i \cap B) \tag{3.20} \end{equation}\]
Aplicando (3.15), pode-se escrever
\[\begin{equation} Pr(B) = \sum_{i} Pr(A_{i}) \cdot Pr(B|A_{i}) \tag{3.21} \end{equation}\]
\(\bigtriangleup\)De (3.13) pode-se calcular a probabilidade de \(A_{i}\) dada a ocorrência de \(B\) por
\[\begin{equation} Pr(A_{i}|B) = \dfrac{Pr(A_{i} \cap B)}{Pr(B)} \tag{3.22} \end{equation}\]
Aplicando (3.21) no denominador e (3.15) no numerador de (3.22), \[\begin{equation} Pr(A_{i}|B) = \dfrac{Pr(A_{i}) \cdot Pr(B|A_{i})}{\sum_{j} Pr(A_{j}) \cdot Pr(B|A_{j})} \tag{3.23} \end{equation}\]
Este é o Teorema de Bayes, útil quando conhecemos as probabilidades condicionais de \(B\) dado \(A_{i}\), mas não diretamente a probabilidade de \(B\). Conhecida também como Regra de Bayes ou ainda a probabilidade da causa dada a consequência.
pa1 = 1/3
pa2 = 2/3
pba1 = 1/2
pba2 = 1
(pa1b = (pa1*pba1)/(pa1*pba1+pa2*pba2))## [1] 0.23.6 Variáveis Aleatórias Discretas
3.6.1 Definição
Uma variável aleatória (v.a.) é uma transformação (função) de \(\Omega\) em \(\mathbb{R}^n\). Isto significa que os resultados dos experimentos aleatórios serão transformados em números. Considere uma variável aleatória \(X\). \(R_{X}\) é o conjunto de todos os possíveis valores de \(X\), chamado contradomínio. Ele pode ser considerado um “espaço amostral numérico” obtido a partir de \(\Omega\). Uma variável aleatória discreta é tal que \(R_{X}\) é finito ou infinito enumerável.
\(\\\)
a. Defina o contradomínimo da variável \(Y\): ‘diferença dos pontos.’
b. Defina o contradomínimo da variável \(W\): ‘produto dos pontos.’
c. Defina o contradomínimo da variável \(Q\): ‘quociente dos pontos.’
3.6.2 Distribuição de probabilidade
Seja \(X\) uma variável aleatória discreta, onde para cada ponto de \(R_{X}\) associa-se uma (função massa de) probabilidade ou distribuição de probabilidade \(p(x) = Pr(X=x)\), satisfazendo \(p(x) \ge 0\) para todo \(x\) e \(\sum_{x \in R_{X}} p(x) = 1\).
a. Do Exemplo 3.20.
b. Do Exercício 3.5.
\(\\\)
a. Refaça para três lançamentos.
b. Refaça para quatro lançamentos.
c. Refaça para \(n\) lançamentos.
3.6.3 Esperança, variância e desvio padrão
A esperança de uma variável aleatória discreta \(X\) é dada por
\[\begin{equation} E\left[ X \right] = \sum_{x} x \cdot p(x) \tag{3.24} \end{equation}\]
A esperança de uma função \(g(X)\) é dada por
\[\begin{equation} E\left[ g(X) \right] = \sum_{x} g(x) \cdot p(x) \tag{3.25} \end{equation}\]
A variância de uma variável aleatória discreta \(X\) é dada por
\[\begin{equation} V(X) = E( \left[ X - E(X) \right] ^2) = E(X^2) - \left[ E(X) \right] ^2 \tag{3.26} \end{equation}\]
O desvio padrão de uma variável aleatória discreta \(X\) é dado por
\[\begin{equation} D(X) = \sqrt{V(X)} \tag{3.27} \end{equation}\]
3.6.4 Distribuições discretas especiais
3.6.4.1 Distribuição Binomial \(\cdot \; \mathcal{B}(n,p)\)
Considere um único lançamento de uma moeda que resulta em cara (\(H\)) ou coroa (\(T\)). Seja \(Pr(\{ H \})=p\) e \(Pr(\{ T \})=1-p\). Este é um experimento ou ensaio de Bernoulli. Suponha agora \(n\) lançamentos independentes da mesma moeda. Este é um experimento binomial. Seja \(X\) o número de faces cara resultantes nos \(n\) lançamentos independentes. \(X\) é uma variável aleatória (com distribuição) (de probabilidades) binomial de parâmetros \(n\) e \(p\), denotado por \(X \sim \mathcal{B}(n,p)\). A distribuição binomial é dada por
\[\begin{equation} p(x) = Pr(X=x) = {n \choose x}p^{x}(1-p)^{n-x} \tag{3.28} \end{equation}\]
onde \(n \in \mathbb{N}, p \in \left[ 0,1 \right]\), \(x \in \left\lbrace 0, \ldots, n \right\rbrace\) e
\[\begin{equation} {n \choose x} = {n \choose n-x} = C_{n}^{x} = \frac{{n!}}{{x!\left( {n - x} \right)!}} \tag{3.29} \end{equation}\]
A esperança e variância são dadas por
\[\begin{equation} E(X)=np \tag{3.30} \end{equation}\]
\[\begin{equation} V(X)=np(1-p) \tag{3.31} \end{equation}\]
barplot(dbinom(0:12, 12, 0.7), main = 'B(12,0.7)', names.arg = 0:12)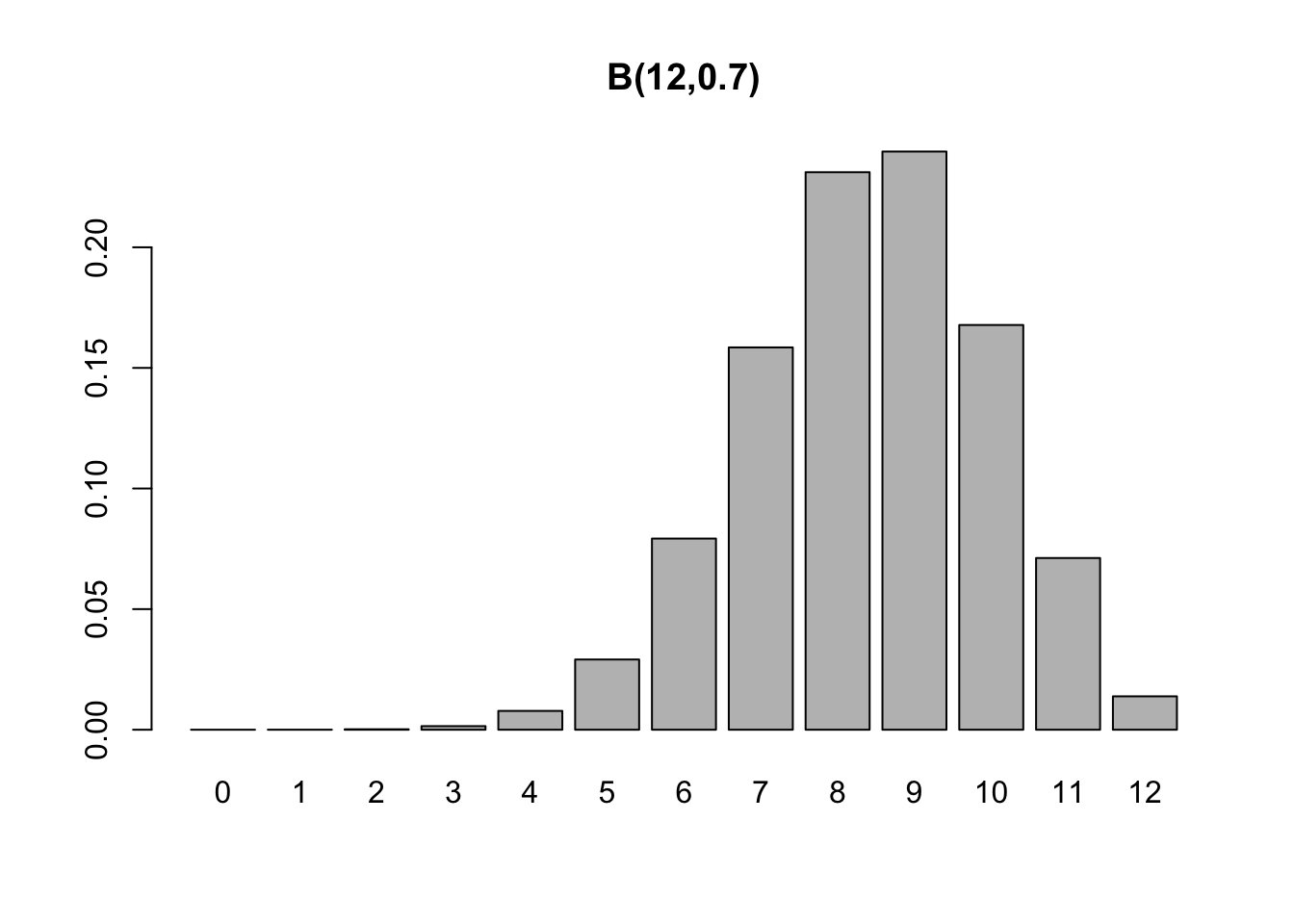
3.6.4.2 Distribuição Binomial Negativa \(\cdot \; \mathcal{BN}(k,p)\)
Considere novamente o lançamento de uma moeda que resulta em cara (\(H\), sucesso) ou coroa (\(T\), fracasso) onde \(Pr(\{ H \})=p\) e \(Pr(\{ T \})=1-p\). Seja \(X\) o número de lançamentos (ensaios de Bernoulli) realizados até atingir a \(k\)-ésima cara (\(k\)-ésimo sucesso). \(X\) é uma variável aleatória (com distribuição) (de probabilidades) binomial negativa de parâmetros \(k\) e \(p\), denotada por \(X \sim \mathcal{BN}(k,p)\), onde \[ k \in \{1,2,\ldots\}, 0 \le p \le 1, x \in \{k,k+1,\ldots\} \] e definida por
\[\begin{equation} p(x) = Pr(X=x) = {x-1 \choose k-1}p^{k}(1-p)^{x-k} \tag{3.32} \end{equation}\]
onde
\[\begin{equation} {x-1 \choose k-1} = C_{k-1}^{x-1} = \frac{{(x-1)!}}{{(k-1)! (x-k)!}} \tag{3.33} \end{equation}\]
A esperança e variância são dadas por
\[\begin{equation} E(X)=k/p \tag{3.34} \end{equation}\]
\[\begin{equation} % V(X)=\dfrac{k(1-p)}{p^2} \tag{3.35} V(X)=k(1-p)/p^2 \end{equation}\]
\[ E(X) = 4/0.7 = 40/7 \approx 5.714286, \] \[ V(X)= 4 \times (1-0.7)/0.7^2 = 120/49 \approx 2.44898 \]
\[ D(X) = \sqrt{2.44898} \approx 1.564922. \]
barplot(dnbinom(0:10, 4, 0.7), main = 'BN(4,0.7)', names.arg = 4:14)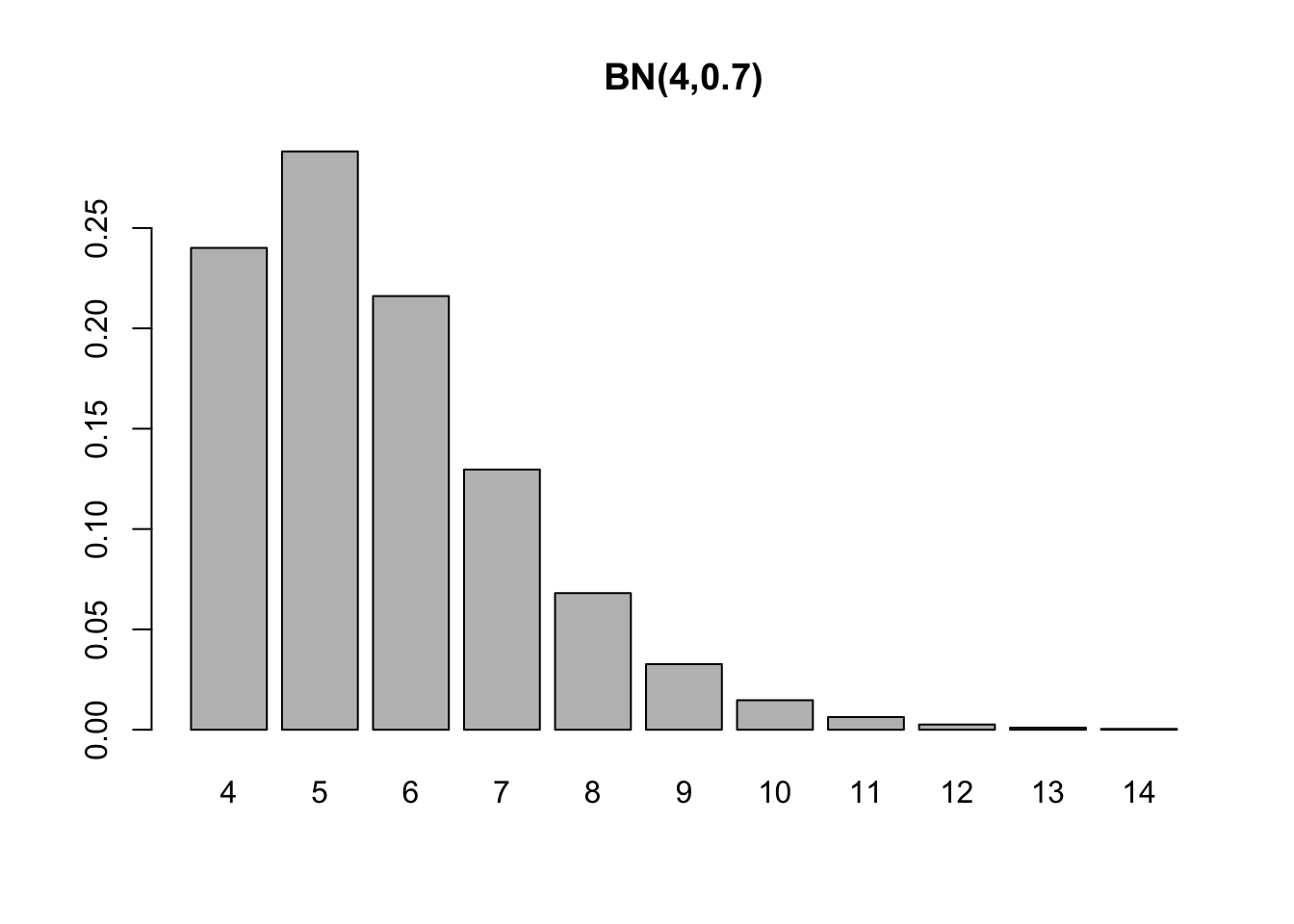
3.6.4.3 Distribuição Poisson \(\cdot \; \mathcal{P}(\lambda)\)
Poisson (1837) abordou a distribuição que leva seu nome considerando o limite de uma sequência de distribuições binominais conforme Equação (3.28), no qual \(n\) tende ao infinito e \(p\) tende a zero enquanto \(np\) permanece finito igual a \(\lambda\).
A distribuição de Poisson é dada por
\[\begin{equation} p(x) = Pr(X=x) = \frac{{e^{ - \lambda } \lambda ^x }}{{x!}} \tag{3.36} \end{equation}\]
onde o número de Euler21 tem valor aproximado \(e \approx 2.71828\;18284\;59045\;23536\). A esperança e variância são dadas por \[\begin{equation} E(X)=\lambda \tag{3.37} \end{equation}\]
\[\begin{equation} V(X)=\lambda \tag{3.38} \end{equation}\]
barplot(dpois(0:10, 2), main = 'P(2)', names.arg = 0:10)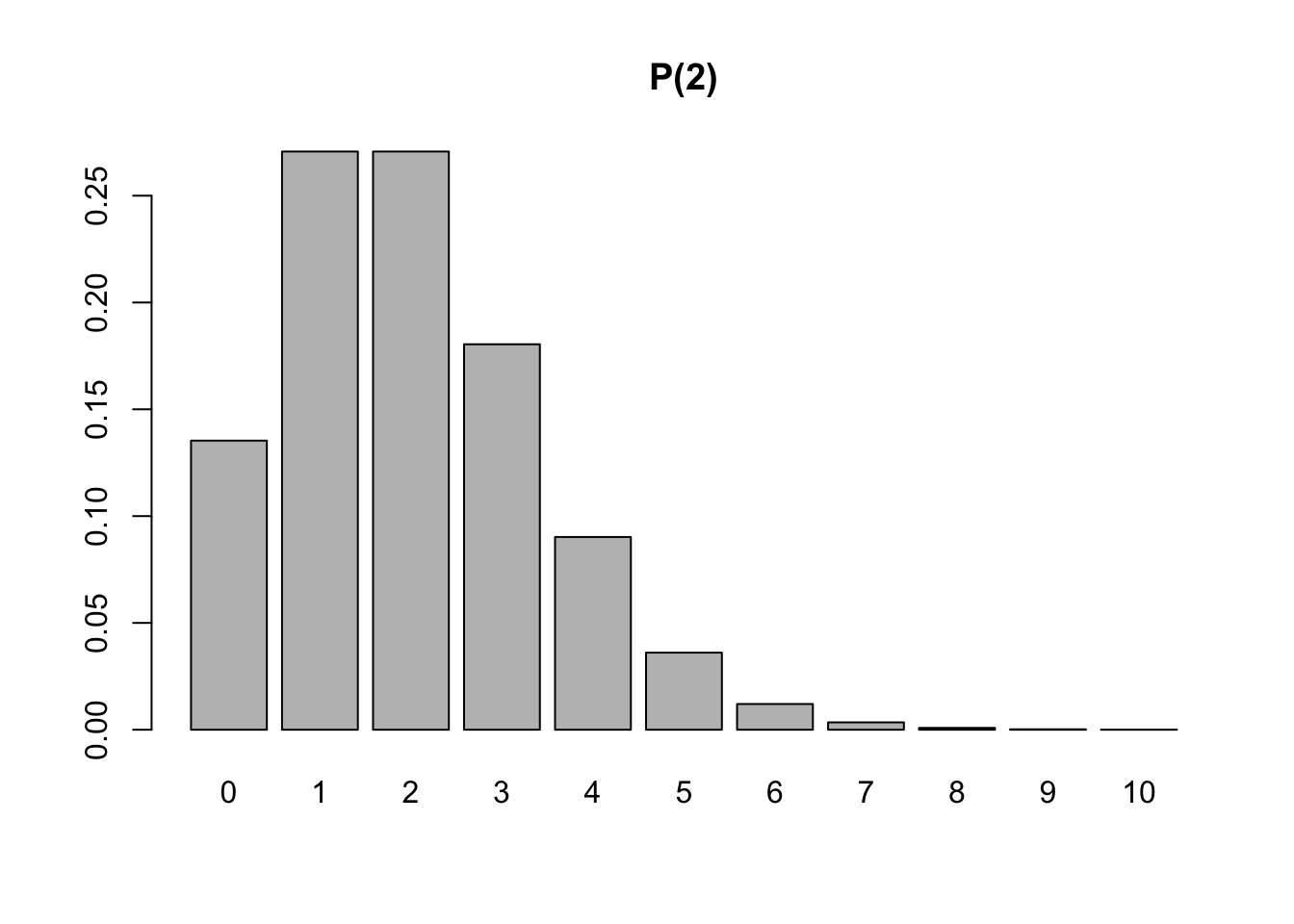
Exercício 3.9 Considere a distribuição de Poisson e a função exponencial definida pela série \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\) (Boros and Moll 2004, 91).
a. Mostre que a função descrita pela Eq. (3.36) é uma função (massa) de probabilidade.
b. Mostre que \(E(X)\) é dada pela Eq. (3.37).
c. Mostre que \(V(X)\) é dada pela Eq. (3.38).
\(\\\)
3.6.4.4 Distribuição Hipergeométrica \(\cdot \; \mathcal{H}(N,R,n)\)
Suponha uma urna com \(N\) bolinhas das quais \(R\) são marcadas com um \(\times\), de onde retira-se uma amostra de \(n\) bolinhas. Seja \(X\) o número de bolinhas marcadas com \(\times\) das \(n\) sorteadas. \(X\) tem distribuição hipergeométrica, denotada por \[ X \sim \mathcal{H}(N,R,n) \] onde \(N \in \{1,2,\ldots\}\), \(R \in \{1,2,\ldots,N\}\), \(n \in \{1,2,\ldots ,N\}\)}. Sua função (massa) de probabilidade é definida por
\[\begin{equation} p(x) = Pr(X=x) = \dfrac{{R \choose x}{N-R \choose n-x}}{{N \choose n}} \tag{3.39} \end{equation}\]
A esperança e variância são dadas por \[\begin{equation} E(X) = n \frac{R}{N} \tag{3.40} \end{equation}\]
\[\begin{equation} V(X) = n \frac{R}{N} \frac{N-R}{N} \frac{N-n}{N-1} \tag{3.41} \end{equation}\]
barplot(dhyper(0:7, 10, 5, 7), main = 'H(15,10,7)', names.arg = 0:7)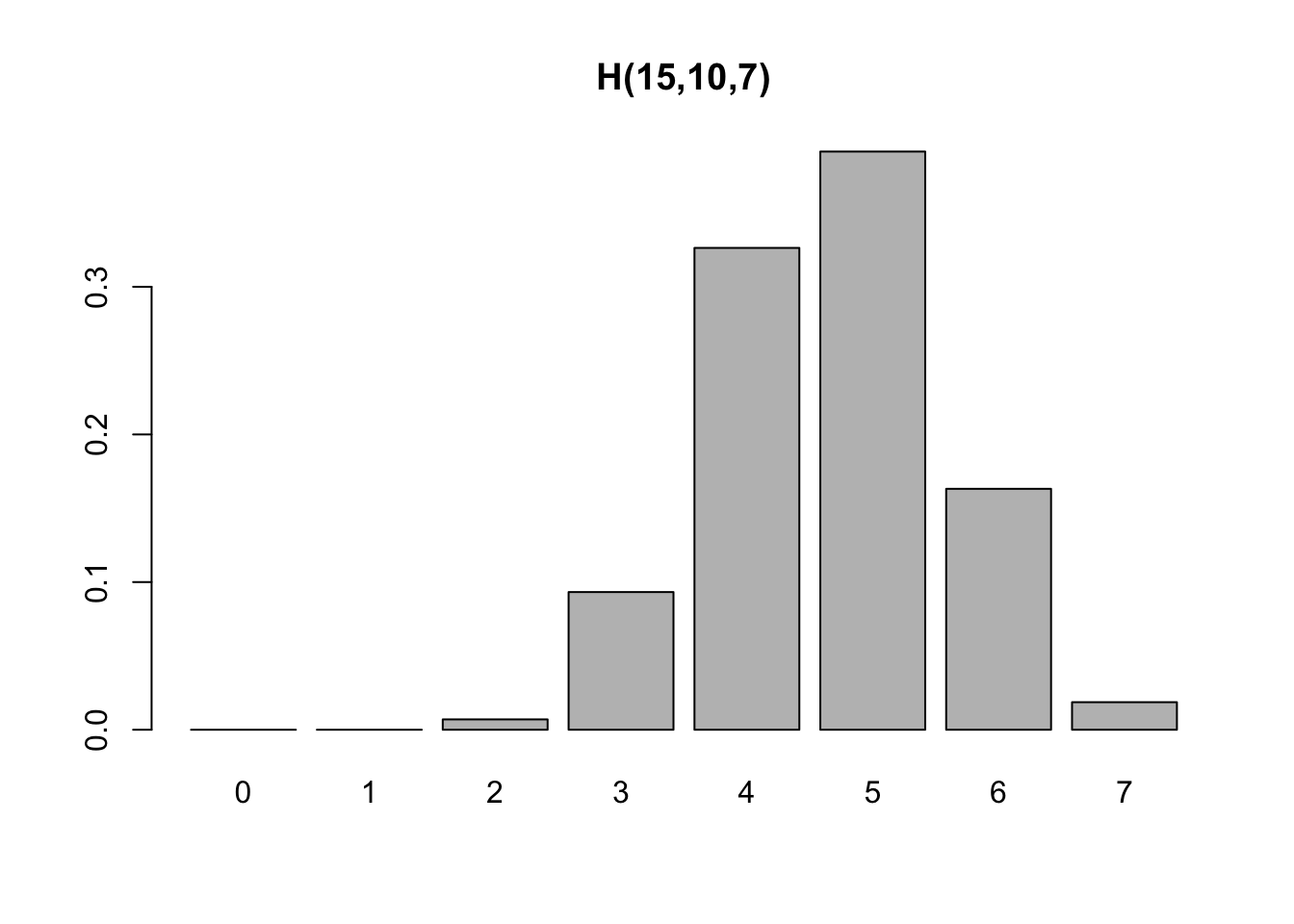
3.6.4.5 Distribução Bernoulli-Poisson
Uma variável aleatória \(X\) possui distrubuição Bernoulli-Poisson parametrizada por \(p\), \(\lambda_1\) e \(\lambda_2\) se assume distribuição Poisson de taxa \(\lambda_1\) com probabilidade \(p\) e distribuição Poisson de taxa \(\lambda_2\) com probabilidade \(1-p\). Simbolicamente \(X \sim \mathcal{BP}(p,\lambda_1,\lambda_2)\), \(x \in \{ 0,1,\ldots \}\), \(p \in \left[ 0,1 \right]\), \(\lambda_1,\lambda_2 > 0\), i.e.,
\[\begin{equation} X \sim \left\{ \begin{array}{l} \mathcal{P}(\lambda_1) \;\; \text{com probabilidade} \;\; p \\ \mathcal{P}(\lambda_2) \;\; \text{com probabilidade} \;\; 1-p \\ \end{array} \right. \tag{3.42} \end{equation}\]
Sua função (massa) de probabilidade é
\[\begin{equation} p(x) = p \frac{e^{-\lambda_1} \lambda_{1}^{x}}{x!} + (1-p) \frac{e^{-\lambda_2} \lambda_{2}^{x}}{x!} \tag{3.43} \end{equation}\]
Sua esperança e variância são dadas por
\[\begin{equation} E(X) = (\lambda_1 - \lambda_2)p + \lambda_2 \tag{3.44} \end{equation}\]
\[\begin{equation} V(X) = -(\lambda_1 - \lambda_2)^2 p^2 + \left[ (\lambda_1 - \lambda_2)^2 + \lambda_1 - \lambda_2 \right] p + \lambda_2 \tag{3.45} \end{equation}\]
Exercício 3.10 Considere a distribuição Bernoulli-Poisson definida pela Eq. (3.43).
a. Mostre que a função descrita pela Eq. (3.43) é uma função (massa) de probabilidade.
b. Mostre que \(E(X)\) é dada pela Eq. (3.44). Dica: \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\)
c. Mostre que \(V(X)\) é dada pela Eq. (3.45).
\(\\\)
3.7 Variáveis Aleatórias Contínuas
Uma variável aleatória é dita contínua quando assume qualquer valor em um intervalo ou coleção de intervalos.
Seja \(X\) uma variável aleatória contínua. Como não é possível listar todos os elementos de \(R_{X}\), a notação \(p(x)\) perde o sentido, visto que \(p(x)\) é zero para todo \(x\). Assim, para tratar do cálculo de probabilidades com variáveis aleatórias contínuas, será utilizado \(f(x)\) no lugar de \(p(x)\). Assim, para cada ponto de \(R_{X}\) associa-se uma (função) densidade (de probabilidade) (fdp) \(f(x)\), satisfazendo
\[\begin{equation} f(x) \ge 0, \forall \; x \tag{3.46} \end{equation}\]
\[\begin{equation} \int_{x} f(x)\;dx = 1 \tag{3.47} \end{equation}\]
\[\begin{equation} Pr(a \leq X \leq b) = \int_{a}^{b} f(x)\;dx \tag{3.48} \end{equation}\]
A fda, (função de) distribuição (acumulada) \(F\) de uma v.a. contínua, é definida como
\[\begin{equation} F(x) = Pr(X \leq x) = \int_{-\infty}^x f(t) \;dt \tag{3.49} \end{equation}\]
Note que \(f(x)=F'(x)\), \(Pr(X=x)=0\) e \(Pr(X \le x) = Pr(X < x)\).
Exemplo 3.30 (fda) Suponha a v.a. \(X\): ‘altura de pessoas da PUCRS’ com fdp \[ f(x) = -\dfrac{46875}{19652} (x^{2} - 3.36x + 2.36), \;\; x \in \left[ 1.00,2.36 \right]. \] Por (3.49), a função distribuição acumulada de \(X\) é
\[\begin{align*} F(x) =& Pr(X \leq x) \nonumber \\ =& -\dfrac{46875}{19652} \int_{1}^{x} (t^{2} - 3.36t + 2.36) \;dt \nonumber \\ =& -\dfrac{46875}{19652} \left[ \frac{t^{3}}{3} - \frac{3.36t^{2}}{2} + 2.36t \right] \bigg\rvert_{1}^{x} \nonumber \\ =& -\dfrac{46875}{19652} \left( \left[ \frac{x^{3}}{3} - 1.68x^{2} + 2.36x \right] - \left[ \frac{1^{3}}{3} - 1.68 \times 1^{2} + 2.36 \times 1 \right] \right) \nonumber \\ F(x) =& -\dfrac{46875}{19652} \left[ \frac{x^{3}}{3} - 1.68x^{2} + 2.36x - \frac{76}{75} \right] \nonumber \end{align*}\]f <- function(x) (-46875/19652)*(x^2-3.36*x+2.36)
integrate(f,1,2.36)## 1 with absolute error < 1.1e-143.7.1 Esperança, variância e desvio padrão
A esperança de uma variável aleatória contínua \(X\) é dada por \[\begin{equation} E(X) = \int_{x} x \cdot f(x)\;dx \tag{3.50} \end{equation}\]
A esperança de uma função \(g(X)\) é dada por \[\begin{equation} E(g(X)) = \int_{x} g(x) \cdot f(x)\;dx \tag{3.51} \end{equation}\]
A variância de uma variável aleatória contínua \(X\) é dada tal como no caso discreto indicado pela Eq. (3.26). Da mesma forma o desvio padrão é a raiz quadrada da variância, tal como indicado na Eq. (3.27).
3.7.2 Distribuições contínuas especiais
3.7.2.1 Distribuição Uniforme Contínua \(\cdot \; \mathcal{U}(a,b)\)
A distribuição uniforme no intervalo \(\left[ a,b \right]\) tem sua (função) densidade (de probabilidade) definida por
\[\begin{equation} f(x) = \dfrac{1}{b-a} \tag{3.52} \end{equation}\]
Função distribuição acumulada \[\begin{equation} F(x) = Pr(X<x) = \dfrac{x-a}{b-a} \tag{3.53} \end{equation}\]
Esperança \[\begin{equation} E(X) = \dfrac{a+b}{2} \tag{3.54} \end{equation}\]
Variância \[\begin{equation} V(X) = \dfrac{(b-a)^2}{12} \tag{3.55} \end{equation}\]
3.7.2.2 Distribuição Normal univariada \(\cdot \; \mathcal{N}(\mu,\sigma)\)
A distribuição normal univariada ou gaussiana (em homenagem a Johann Carl Friedrich Gauss) é anotada por \(\mathcal{N}(\mu,\sigma)\) e dada pela expressão \[\begin{equation} f(x|\mu, \sigma) = \dfrac{1}{\sqrt{2\pi} \sigma} \exp \bigg\{ -\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right) ^2 \bigg\} \tag{3.58} \end{equation}\]
para \(x \in \rm I\!R\), \(\mu \in \rm I\!R\), \(\sigma > 0\). Os parâmetros \(\mu\) e \(\sigma\) podem ser calculados respectivamente pelas Equações (2.8) e (2.21).
A distribuição normal padrão univariada é dada pela expressão \[\begin{equation} f(z|\mu=0, \sigma=1) = \dfrac{1}{\sqrt{2\pi}} \exp \bigg\{ -\frac{z^2}{2} \bigg\} \tag{3.59} \end{equation}\]
para \(z \in \rm I\!R\).
# gráfico da densidade da normal padrão N(0,1) rápido e fácil
curve(dnorm(x), -3, 3)
# gráfico da densidade da normal padrão N(0,1) via ggplot2
library(ggplot2)
ggplot(data.frame(x = -3:3), aes(x, alpha = 0.05)) +
stat_function(fun = dnorm, args = c(0, 1), geom = 'area',
xlim = c(-3, qnorm(0.025)), fill = 'lightgreen') +
stat_function(fun = dnorm, args = c(0, 1), geom = 'area',
xlim = c(-1, 1), fill = 'lightblue') +
stat_function(fun = dnorm, args = c(0, 1), geom = 'area',
xlim = c(qnorm(0.95), 3), fill = 'red1') +
stat_function(fun = dnorm, args = c(0, 1), show.legend = FALSE) +
xlab('Z') + ylab('Densidade') +
theme(legend.position = 'none')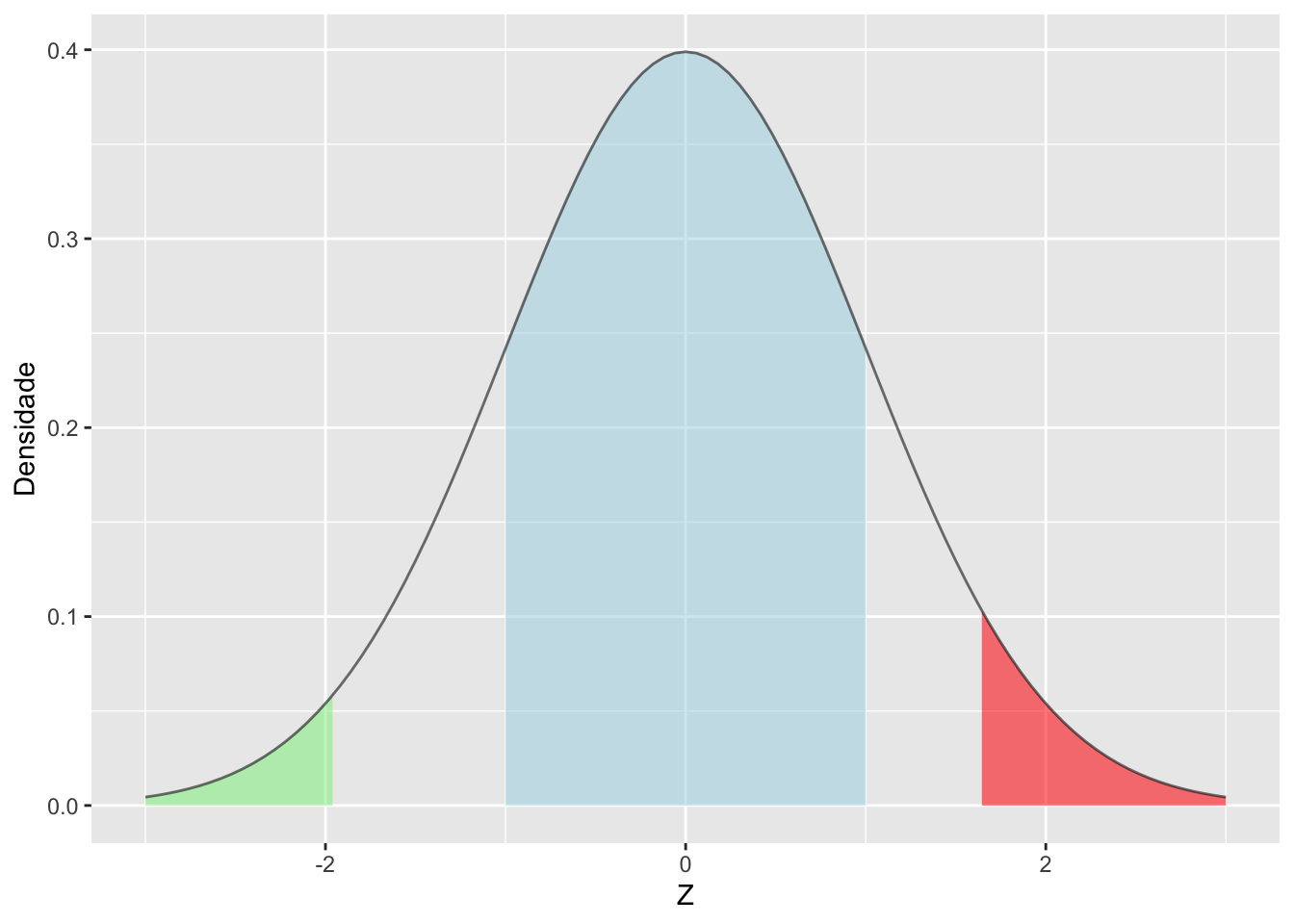
# distribuição acumulada
pnorm(0) # Pr(Z ≤ 0) = Pr(Z > 0), distribuição simétrica## [1] 0.5# quantis (separatrizes)
qnorm(0.5) # q tal que Pr(Z ≤ q) = Pr(Z > q) = 0.500, distribuição simétrica## [1] 0Exercício 3.15 Considere a variável aleatória \(Z\) com distribuição normal padrão anotada por \(Z \sim \mathcal{N}(0,1)\). Obtenha as seguintes quantidades:
a. \(Pr(Z \le -1.96)\).
b. \(Pr(-1 \le Z \le 1)\).
c. \(Pr(Z > 1.64)\).
d. \(q\) tal que \(Pr(Z \le q) = 0.025\).
e. \(q\) tal que \(Pr(-q \le Z \le q) = 0.6826894921\).
f. \(q\) tal que \(Pr(Z > q) = 0.05\).
\(\\\)
3.7.3 Normal bivariada
A distribuição normal bivariada é anotada por \(\mathcal{N}(\mu_1,\mu_2,\sigma_1,\sigma_2,\rho)\) e dada pela expressão \[\begin{equation} f(x_1,x_2|\mu_1, \mu_2, \sigma_1, \sigma_2, \rho) = \\ \;\;\; \tfrac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \exp \Bigg\{ -\tfrac{1}{2(1-\rho^2)} \left[ \tfrac{(x_1-\mu_1)^2}{\sigma^2_1} + \tfrac{(x_2-\mu_2)^2}{\sigma^2_2} - \tfrac{2 \rho (x_1 - \mu_1) (x_2 - \mu_2)}{\sigma_1 \sigma_2} \right] \Bigg\} \tag{3.60} \end{equation}\]
para \(x_1, x_2 \in \rm I\!R\), \(\mu \in \rm I\!R^{2}\), \(\sigma_1, \sigma_2 \ge 0\), \(\sigma_{12} \in \rm I\!R\), \(-1 \le \rho \le +1\). O vetor \(\boldsymbol{\mu}' = \begin{bmatrix} \mu_{1} & \mu_{2} \end{bmatrix}\) é dado conforme Eq. (3.61), a matriz de covariâncias \(\Sigma = \begin{bmatrix} \sigma_{1}^2 & \sigma_{12} \\ \sigma_{12} & \sigma_{2}^2 \end{bmatrix}\) conforme Eq. (3.62) e a matriz de correlação \(\boldsymbol{\rho} = \begin{bmatrix} 1 & \rho \\ \rho & 1 \end{bmatrix}\) conforme Eq. (3.63).
\[\begin{equation} \boldsymbol{\mu} = \begin{bmatrix} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{p} \end{bmatrix} \tag{3.61} \end{equation}\]
\[\begin{equation} \Sigma = Cov(X) = \begin{bmatrix} \sigma_{1}^2 & \sigma_{12} & \cdots & \sigma_{1p} \\ \sigma_{12} & \sigma_{2}^2 & \cdots & \sigma_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{1p} & \sigma_{2p} & \cdots & \sigma_{p}^2 \end{bmatrix} = \begin{bmatrix} \sigma_{1}^2 & \rho_{12} \sigma_1 \sigma_2 & \cdots & \rho_{1p} \sigma_1 \sigma_p \\ \rho_{12} \sigma_1 \sigma_2 & \sigma_{2}^2 & \cdots & \rho_{2p} \sigma_2 \sigma_p \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{1p} \sigma_1 \sigma_p & \rho_{2p} \sigma_2 \sigma_p & \cdots & \sigma_{p}^2 \end{bmatrix} \tag{3.62} \end{equation}\]
\[\begin{equation} \boldsymbol{\rho} = Cor(X) = \begin{bmatrix} 1 & \rho_{12} & \cdots & \rho_{1p} \\ \rho_{12} & 1 & \cdots & \rho_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{1p} & \rho_{2p} & \cdots & 1 \end{bmatrix} \tag{3.63} \end{equation}\]
# parâmetros
n <- 100
x1 <- seq(-5, 5, length = n)
x2 <- seq(-5, 5, length = n)
m1 <- 0; m2 <- 0 # médias
s1 <- 1; s2 <- 2 # desvios padrão
# Caso 1: produto de normais independentes, \rho = 0
z1 <- outer(x1, x2, function(x,y) dnorm(x,m1,s1) * dnorm(y,m2,s2))
# gráficos
library(rgl)
persp3d(x1, x2, z1, col = 'gray')
rglwidget()# Caso 2: via mvtnorm::dmvnorm, \rho = 0 (note que sigma é a matriz de covariâncias)
library(mvtnorm)
m <- c(m1,m2)
s <- diag(c(s1^2, s2^2))
z2 <- outer(x1, x2, function(x,y) dmvnorm(cbind(x,y), mean = m, sigma = s))
# gráficos
library(rgl)
persp3d(x1, x2, z2, col = 'lightblue')
rglwidget()sigma da função dmvnorm ser a matriz de covariâncias (e não de correlações), sabe-se da Eq. (4.3) que a correlação \(\rho_{jk}\) é obtida dividindo-se a covariância \(\sigma_{jk}\) pelo produto dos desvios padrão \(\sigma_{j}\) e \(\sigma_{k}\). Assim, \[ \sigma_{jk} = \rho_{jk}\sigma_{j}\sigma_{k} \]
# parâmetros
n <- 100
x1 <- seq(-5, 5, length = n)
x2 <- seq(-5, 5, length = n)
m1 <- 0; m2 <- 0 # médias
s1 <- 1; s2 <- 2 # desvios padrão
rho <- 0.9 # correlação
s12 <- rho*s1*s2 # covariância
# via mvtnorm::dmvnorm, \rho = 0.9
library(mvtnorm)
m <- c(m1,m2)
s <- matrix(c(s1^2, s12, s12, s2^2), nrow = 2, byrow = T)
z3 <- outer(x1, x2, function(x,y) dmvnorm(cbind(x,y), mean = m, sigma = s))
# gráficos
library(rgl)
persp3d(x1, x2, z3, col = 'lightgreen')
rglwidget()As probabilidades podem ser calculadas através da função pmvnorm do pacote mvtnorm.
library(mvtnorm)
# parâmetros
m <- c(0,0)
s <- diag(2)
# Pr(X1 < 0, X2 < 0)
lower <- c(-Inf, -Inf)
upper <- c(0, 0)
pmvnorm(lower, upper, m, s)## [1] 0.25
## attr(,"error")
## [1] 1e-15
## attr(,"msg")
## [1] "Normal Completion"3.7.4 Normal multivariada
A distribuição normal multivariada é anotada por \(\mathcal{N}(\boldsymbol{\mu},\Sigma)\) e definida pela expressão \[\begin{equation} f(\boldsymbol{x}|\boldsymbol{\mu}, \Sigma) = \dfrac{1}{\sqrt{2\pi} |\Sigma|^{1/2}} \exp \bigg\{ -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})' \Sigma^{1/2} (\boldsymbol{x} - \boldsymbol{\mu}) \bigg\} \tag{3.64} \end{equation}\]
para \(\boldsymbol{x} \in \rm I\!R^{n}\), \(\boldsymbol{\mu} \in \rm I\!R^{n}\), \(\sigma_{ij} \ge 0\) se \(i = j\), \(\sigma_{ij} \in \rm I\!R\) se \(i \ne j\). O vetor de médias \(\boldsymbol{\mu}\) é dado conforme Eq. (3.61), e a matriz de covariâncias \(\Sigma\) conforme Eq. (3.62).
(Tong 1990) apresenta ‘algumas propriedades fundamentais’ da distribuição normal multivariada na Seção 1.1.1 (pp. 1-2).
- Representa uma extensão natural da distribuição normal univariada e fornece um modelo adequado para muitos problemas da vida real
- Pelo Teorema Central do Limite a distribuição do vetor de médias da amostra é assintoticamente normal, permitindo o uso da distribuição normal multivariada para aproximar distribuições de médias para amostras grandes
- A função densidade de uma distribuição normal multivariada é determinada exclusivamente pelo vetor de médias e a matriz de covariância da variável aleatória \(X\)
- Correlações zero implicam independência
- A família de distribuições normais multivariadas é fechada sob transformações lineares e combinações lineares, i.e., as distribuições de transformações lineares ou combinações lineares de variáveis normais multivariadas são novamente normais multivariadas
- A distribuição marginal de qualquer subconjunto de componentes de uma variável normal multivariada também é normal multivariada
- A distribuição condicional em uma distribuição normal multivariada é multivariada normal
- Para a distribuição normal multivariada, as propriedades de dependência positiva e negativa dos componentes de um vetor aleatório são completamente determinadas pelo sinal e pelo tamanho do coeficiente de correlação
mvtnorm::rmvnorm.
library(mvtnorm)
set.seed(111) # para garantir reprodutibilidade
sim1 <- rmvnorm(1000, mean = c(100,20,0,-10), sigma = diag(4))
colMeans(sim1) # vetor de médias (amostrais)## [1] 99.9403 20.0350 0.0131 -9.9727cov(sim1) # matriz de covariâncias (amostrais)## [,1] [,2] [,3] [,4]
## [1,] 0.9798 0.0147 0.0256 0.0149
## [2,] 0.0147 1.0232 -0.0581 0.0242
## [3,] 0.0256 -0.0581 0.9681 0.0373
## [4,] 0.0149 0.0242 0.0373 1.0024cor(sim1) # matriz de correlação (amostral)## [,1] [,2] [,3] [,4]
## [1,] 1.0000 0.0147 0.0263 0.0150
## [2,] 0.0147 1.0000 -0.0583 0.0239
## [3,] 0.0263 -0.0583 1.0000 0.0379
## [4,] 0.0150 0.0239 0.0379 1.0000mvtnorm.a. Simule \(n=2000\) valores de uma normal multivariada de \(p=4\) dimensões tal que \(\mu_1 = 100\), \(\mu_2 = 0\), \(\mu_3 = -10\), \(\mu_4 = -200\), \(\rho_{12}=0.2\), \(\rho_{13}=-0.5\), \(\rho_{14}=0.8\), \(\rho_{23}=-0.1\), \(\rho_{24}=-0.7\), \(\rho_{34}=0.01\), \(\sigma_1=15\), \(\sigma_2=1\), \(\sigma_3=2\), \(\sigma_4=25\).
b. Calcule o vetor de médias e as matrizes de covariância e correlação a partir dos valores simulados. Compare com os valores utilizados na geração pseudo-aleatória.
c. Calcule \(Pr(X_1<70, X_2<1.96, X_3<0, X_4<-50)\).
d. Calcule \(Pr(X_1>70, X_2<1.96, X_3>0, X_4<-50)\).
e. Calcule \(Pr(70<X_1<120, X_2<1.96, X_3>0, -125<X_4<-50)\).
3.7.5 Para saber mais
(Patel and Read 1982) trazem uma coleção de resultados e propriedades relacionados à distribuição normal. (Tong 1990) fornece um tratamento abrangente de resultados relacionados à distribuição normal multivariada. Os temas principais são dependência, desigualdades de probabilidade e seus papéis na teoria e aplicações.
3.7.5.1 Distribuição exponencial \(\cdot \; \mathcal{E}(\lambda)\)
Considere novamente o pedágio descrito na Seção 3.6.4.3, onde passam em média \(\lambda\) veículos por minuto. Pode-se inverter a leitura, colocando o tempo entre cada carro como a nova variável de interesse. Assim, neste pedágio passa 1 carro a cada \(\frac{1}{\lambda}\) minutos. A variável aleatória contínua \(X\): ‘tempo entre veículos’ tem distribuição exponencial de parâmetro \(\lambda\), denotada por \[ X \sim \mathcal{E}(\lambda), \] onde \(\lambda > 0\) e \(x > 0\). A função densidade exponencial é dada por \[\begin{equation} f(x) = \lambda e^{-\lambda x} \tag{3.65} \end{equation}\] onde \(e\) é o número de Euler. Sua função distribuição acumulada é dada por \[\begin{equation} F(x) = Pr(X \le x) = 1 - e^{-\lambda x} \tag{3.66} \end{equation}\] A esperança e variância são dadas por \[\begin{equation} E(X)= \frac{1}{\lambda} = \lambda^{-1} \tag{3.67} \end{equation}\] \[\begin{equation} V(X)=\frac{1}{\lambda^2} = \lambda^{-2} \tag{3.68} \end{equation}\]
a. Defina \(F(x)\).
b. Obtenha \(Pr(X<1)\).
c. Obteha \(Pr(X>2)\).
d. Faça o esboço do gráfico de \(f(x)\).
\(\\\)
3.8 R como um conjunto de tabelas estatísticas
(Venables et al. 2020) apontam que um uso conveniente de R é fornecer um conjunto abrangente de tabelas estatísticas. Funções são fornecidas para avaliar a função densidade de probabilidade (FDP) \(f(x)\), a função distribuição acumulada (FDA) \(F(x) = Pr(X \le x)\), a função quantil (dado \(q\), o menor \(x\) tal que \(Pr(X \le x) > q\)) e também para simular valores das distribuições. Utiliza-se o prefixo d para a densidade, p para o FDA, q para a função de quantil e r para simulação pseudo-aleatória. A seguir são apresentadas as distribuições de probabilidade disponíveis no base R. Para mais distribuições podem-se utilizar os pacotes adicionais mvtnorm (normal e t multivariadas) e VGAM (Dirichlet, multinomial, beta-binomial, entre outras).

3.9 Exercícios
a. Em um grupo de pessoas que pedem financiamento, qual a probabilidade de uma pessoa ter mais de 33 anos?
b. Neste mesmo grupo, qual a probabilidade de uma pessoa ter idade entre 32 e 40 anos?
c. Se \(Pr(X < x) = 0.6217\), qual o valor de \(x\)?
d. Interprete o valor de \(x\) no contexto do problema. \(\\\)
a. A fábrica oferece garantia de 1 ano. Qual a probabilidade de uma geladeira estragar neste período?
b. Qual a probabilidade de uma geladeira estragar fora da garantia?
c. Qual a probabilidade de uma geladeira falhar entre o primeiro e o segundo ano de uso?
d. Qual a probabilidade de uma geladeira durar mais de 2 anos sem apresentar falhas?
e. Se a fábrica produziu 80 mil geladeiras, quantas pessoas devem acionar a garantia?
\(\\\)
a. No caixa convencional, qual a probabilidade de você esperar mais de 20 minutos para ser atendido? E no caixa prioritário?
b. Você leva em torno de meia hora para ler o caderno de esportes do jornal. Qual a probabilidade de você terminar a leitura enquanto espera na fila do caixa? Faça as contas para ambos os caixas e compare.
c. Uma vovó de 90 anos chegou no banco. Qual a probabilidade de ela esperar entre 20 e 25 minutos para ser atendida?
d. Há uma grande placa indicando que o tempo de espera máximo é de 12 minutos para os clientes preferenciais e 18 minutos para os demais clientes. Com que frequência as pessoas esperam mais do que este tempo para serem atendidas?
e. Você foi chamado para corrigir este tempo máximo. A orientação é que apenas 10% dos clientes sejam atendidos em um tempo maior que o indicado. Qual deveria ser o novo tempo para o caixa preferencial? E para o caixa convencional?
\(\\\)
a. Selecionando ao acaso um candidato, qual a probabilidade de ele ter tirado menos que 5 na prova?
b. Qual a probabilidade de um candidato ter notas entre 5 e 6?
c. Aproximadamente quantas pessoas tiraram notas entre 5 e 6?
d. Qual a nota mínima para obter a aprovação?
\(\\\)
a. Qual a probabilidade de o lucro líquido ser maior que 20 mil reais?
b. Qual a probabilidade de o lucro líquido estar entre 13 mil e 22 mil reais?
c. Qual a probabilidade de a loja dar prejuízo?
\(\\\)
Referências
“[L]a théorie des probabilités n’est au fond, que le bon sens réduit au calcul.” (Laplace 1825) página 275.↩︎
“PROBABILITY DOES NOT EXIST.” (Finetti 1974) página x.↩︎
Há algum tempo era também referenciado como conjunto nulo, mas este termo atualmente designa uma definição formal em Teoria da Medida, onde um conjunto nulo é tal que \(\mu(\phi) = 0\).↩︎
O diagrama de Venn é uma representação gráfica de conjuntos através de círculos ou outras formas.↩︎
Termo técnico indicando que cada moeda possui uma face cara e outra face coroa, ambas com probabilidade \(\frac{1}{2}\) de ocorrência.↩︎
Na literatura também pode ser conhecido como número de Napier, constante de Napier/neperiana, entre outras formas. Não confundir com a constante de Euler–Mascheroni \(\gamma \approx 0.57721\;56649\;01532\;86061\).↩︎