Capítulo 1 Introdução

O Método Estatístico ou simplesmente Estatística reúne ferramentas teóricas e práticas para analisar informações quantitativas, medir incertezas e auxiliar na tomada de decisão. É um componente do Método Científico, e pode ser dividido conforme o esquema da Figura a seguir. Neste curso serão abordados tópicos de Estatística Descritiva,, Inferência Estatística sob os prismas da Estatística Clássica (ou Frequentista) e Bayesiana e Séreis Temporais.

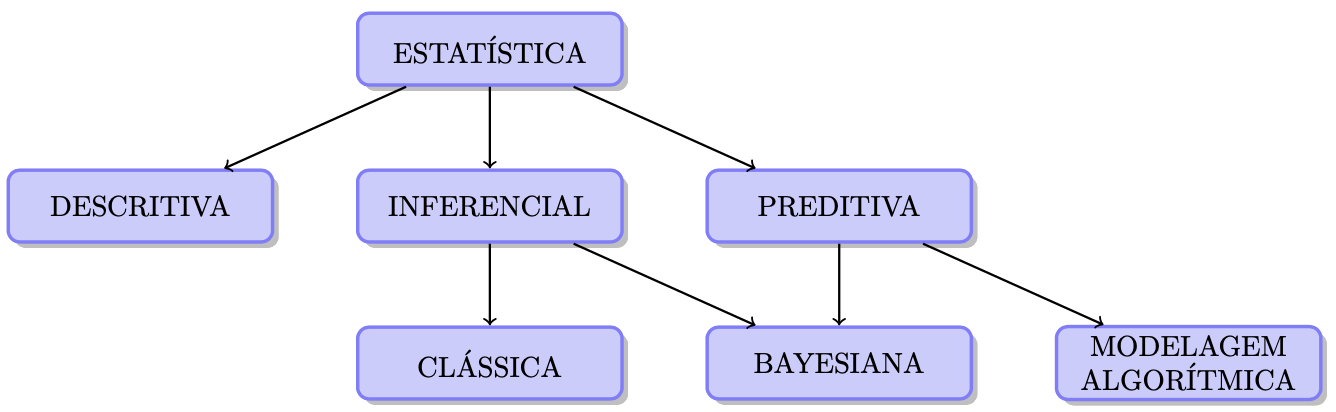
Uma possível divisão da Estatística.

1.1 Ferramentas

1.1.1 R

R é uma ferramenta para cálculos estatísticos e gráficos. Foi desenvolvido no departamento de Estatística da Universidade de Auckland, e seu código está disponível sob a licença GNU (GNU is Not Unix) GPL4. Atualmente a R Foundation está sediada na Universidade de Economia e Negócios de Viena, Áustria. Foi influenciado por linguagens como S e Scheme seguindo o conceito minimalista orientado a objeto, que especifica um pequeno núcleo padrão acompanhado de pacotes para a extensão da linguagem.

Recomenda-se manter o R e seus pacotes sempre atualizados. No Windows recomenda-se ainda a instalação do Rtools de acordo com a versão instalada do R. Os pacotes utilizados neste curso podem ser instalados e atualizados conforme código abaixo. No caso de utilização de sistema operacional do tipo Unix, recomenda-se rodar as instruções acima em um terminal após executar o comando sudo R seguido da senha do sistema. 

packs <- c('tidyverse','readxl','e1071','arrangements','DescTools','symmetry',
           'mvtnorm','VGAM','chisq.posthoc.test','rgl','ggfortify','factoextra',
           'reticulate','LearnBayes')
install.packages(packs, dep = T)
devtools::install_github('filipezabala/jurimetrics', force=T)
devtools::install_github('filipezabala/voice', force=T)
devtools::install_github('filipezabala/desempateTecnico', force=T)
update.packages(ask = F)

CRAN Task Views

As CRAN Task Views visam fornecer informações sobre os pacotes da CRAN (Comprehensive R Archive Network) relacionados a um determinado tópico. É recomendado verificar os assuntos de interesse dentro das CRAN Task Views para uma abordagem mais completa utilizando a linguagem R.

1.1.2 RStudio

RStudio é um ambiente de desenvolvimento integrado ao R. Possibilita a criação de apresentações e relatórios automáticos em diversos formatos como pdf, html e docx, mesclando linguagens como R, LaTeX, markdown, C, C++, Python, SQL, HTML, CSS, JavaScript, Stan e D3. Está disponível nas edições Desktop, Server juntamente com seus respectivos previews, reunindo as funcionalidades do R de forma parcimoniosa.

1.1.3 Python

Python é uma linguagem de programação interpretada, interativa e orientada a objetos. Ela incorpora módulos, exceções, tipagem dinâmica, tipos de dados dinâmicos de nível muito alto e classes. Oferece suporte a vários paradigmas de programação além da programação orientada a objetos, como a programação procedural e funcional. Ele tem interfaces para muitas chamadas de sistema e bibliotecas, bem como para vários sistemas de janela, e é extensível em C ou C ++. Também pode ser usado como uma linguagem de extensão para aplicativos que precisam de uma interface programável. Finalmente, o Python é portátil: ele roda em muitas variantes do Unix, incluindo Linux e macOS, e no Windows.

Python em R Markdown

O pacote reticulate inclui um mecanismo Python para R Markdown que executa trechos de Python em uma única sessão Python incorporada em sua sessão R, permitindo o acesso a objetos criados em trechos de Python do R e vice-versa.

# Interface de R e Python
library(reticulate)
# repl_python() 
os <- import("os")
os$listdir(".")
##  [1] "02-descritiva.Rmd"        ".Rhistory"                "ei_files"                 "01-introducao.Rmd"       
##  [5] ".DS_Store"                "missfont.log"             "LICENSE"                  "temp.zip"                
##  [9] "preamble.tex"             "index.Rmd"                "03-prob.Rmd"              "Dockerfile"              
## [13] "_deploy.sh"               "latex"                    "07-modelos_lineares.Rmd"  "TinyTeX.tgz"             
## [17] "packages.bib"             "code"                     "05-inferencia-class.Rmd"  "ei.Rmd"                  
## [21] "temp.xlsx"                "_output.yml"              "0ei.Rproj"                "_bookdown_files"         
## [25] "06-inferencia-bayes.Rmd"  "img"                      "_bookdown.yml"            "DESCRIPTION"             
## [29] ".gitignore"               ".RData"                   "09-series_temporais.Rmd"  "style.css"               
## [33] "_book"                    "ei.log"                   "source_rfcv.r"            "10-exercicios_extras.Rmd"
## [37] "11-ref.Rmd"               "now.json"                 "book.bib"                 "08-apr_maquina.Rmd"      
## [41] ".git"                     "data"                     ".Rproj.user"              "toc.css"                 
## [45] "_build.sh"                "04-amostragem.Rmd"
Exercício 1.1 Ler a documentação do reticulate disponível em https://rstudio.github.io/reticulate/.

1.1.4 JASP

JASP é um projeto de código aberto apoiado pela Universidade de Amsterdã. Com interface amigável, oferece procedimentos de análises estatísticas com abordagens clássica e bayesiana. Desenvolvido para análises de publicação, dentre suas principais características, estão:

  • Atualização dinâmica de todos os resultados
  • Layout de planilha e uma interface intuitiva de arrastar e soltar
  • Saída anotada para comunicar seus resultados
  • Integração com o Open Science Framework (OSF)
  • Suporte para formato APA (copie gráficos e tabelas diretamente no Word)

1.1.5 PSPP

PSPP é um programa para análise estatística de dados amostrados. Ele interpreta comandos na linguagem SPSS e produz saída tabular em formato ASCII, PostScript ou HTML. Permite realizar estatísticas descritivas, testes t, ANOVA, regressão linear e logística, medidas de associação, análise de cluster, confiabilidade e análise fatorial, testes não paramétricos e muito mais. Pode ser utilizado com a interface gráfica ou os sinataxe via linha de comando. Uma breve lista de alguns dos recursos do PSPP segue abaixo:

  • Suporte para mais de 1 bilhão de casos (linhas)
  • Suporte para mais de 1 bilhão de variáveis
  • Arquivos de sintaxe e dados compatíveis com os do SPSS
  • Uma escolha de terminal ou interface gráfica do usuário
  • Uma escolha de formatos de saída de texto, postscript, pdf, opendocument ou html
  • Interoperabilidade com Gnumeric, LibreOffice, OpenOffice.Org e outros softwares livres
  • Fácil importação de dados de planilhas, arquivos de texto e fontes de banco de dados
  • A capacidade de abrir, analisar e editar dois ou mais conjuntos de dados simultaneamente. Eles também podem ser mesclados, unidos ou concatenados
  • Uma interface de usuário que suporta todos os conjuntos de caracteres comuns e que foi traduzida para vários idiomas
  • Procedimentos estatísticos rápidos, mesmo em conjuntos de dados muito grandes
  • Sem taxas de licença ou período de expiração
  • Portabilidade; Funciona em muitos computadores diferentes e em muitos sistemas operacionais diferentes

1.1.6 Stan

Stan é uma plataforma de código aberto para modelagem estatística e computação estatística de alto desempenho. É também utilizado para análise de dados e previsão nas ciências sociais, biológicas e físicas, engenharia e negócios. A biblioteca de matemática de Stan fornece funções de probabilidade e álgebra linear. Pacotes de R adicionais fornecem modelagem linear baseada em expressão, visualização da posteriori e validação cruzada de exclusão. Existem interfaces para diversos ambientes de computação populares, tais como RStan (R) e PyStan (Python). Usando a linguagem pode-se obter:

  • Inferência estatística bayesiana completa com amostragem MCMC (NUTS, HMC)
  • Inferência bayesiana aproximada com inferência variacional (ADVI)
  • Estimativa de máxima verossimilhança penalizada com otimização (L-BFGS)

1.2 Materiais de apoio

1.2.1 Página do professor Filipe Zabala

Em filipezabala.com o aluno irá encontrar uma série de materiais de apoio como apostilas, vídeos e artigos. Em github.com/filipezabala estão disponíveis uma série de repositórios criados pelo professor.

Exercício 1.2 Para uma introdução aos conceitos básicos de R, assita aos vídeos disponíveis na playlist Ciência de Dados em software livre.

1.2.2 Khan Academy

A Khan Academy5 possui uma ampla gama de materiais gratuitos em Português, que podem servir de suporte ao aluno durante o curso. A lista a seguir indica os principais fundamentos necessários para o bom desenvolvimento do conteúdo.

  1. Propriedades fundamentais de potenciação, radiciação e frações
  1. Teoria dos Conjuntos
  1. Análise combinatória e axiomas de probabilidade
  1. Funções elementares: linear, polinomial, logarítmica e exponencial
  1. Matrizes, determinantes, decomposições, autovalores e autovetores
  1. Derivadas e integrais

1.3 Algarismos e Números

Um algarismo é um símbolo, enquanto um número expressa uma idéia de quantidade. Números são representados por algarismos, sendo fundamental distinguir estes elementos.

Exemplo 1.1 Se há 20 alunos na sala A outros 30 na sala B, pode-se dizer que, em média, há \(\frac{20+30}{2}=25\) alunos nas duas salas. Esta é uma informação numérica. Se rotularmos o sexo masculino como 0 e o feminino como 1, fica claro que 0 e 1 estão sendo tratados como algarismos, uma vez que não expressam quantidades.

1.4 Porcentagens, Decimais e Milhares

Neste texto será adotado o padrão americano, que utiliza o símbolo de ponto (.) como separador de decimais e vírgula (,) como separador de milhares. Assim, \[\frac{1}{40} = 0.025 = 0.0250 = .025 = 2.5\% = \frac{2.5}{100}.\] Dízimas periódicas serão escritas na forma \(\frac{1}{3} = 0.333... = 0.\bar{3} \approx 0.333 \approx 0.3\). O número \(32,960 = 30,000 + 2,000 + 960\) deve ser lido como ‘trinta e dois mil novecentos e sessenta’.
Esta opção evita muitos problemas, já que muitos softwares estatísticos não são compatíveis com o padrão brasileiro, que utiliza vírgula como separador de decimais e ponto para separar os milhares. Nas anotações pessoais e listas de exercícios poderá ser adotada a notação de preferência do aluno.

1.5 O Senhor \(X\)

Quando avalia-se algo de interesse prático, em geral observam-se nomes longos. Considere a variável

\(X\): ‘número de filhos de mulheres atendidas em um hospital público de Porto Alegre em 2019’.

Esta longa descrição tornará maçante qualquer texto que utilize-o muitas vezes, tornando impraticável a realização de cálculos envolvendo tal característica de interesse. É razoável, portanto, associar descrições longas a símbolos. A letra \(X\) é famosa por simbolizar algo genérico, tanto na Ciência quanto na vida cotidiana. Note que o símbolo utilizado para separar \(X\) de sua descrição é :, e não =.

Neste texto será utilizado \(X\) (maiúsculo) para representar a característica de interesse, e \(x_k\) (minúsculo) para representar o \(k\)-ésimo valor observado desta característica. Assim, enquanto \(X\) representa genericamente o número de filhos de mulheres atendidas em um hospital público de Porto Alegre em 2019, \(x_4 = 2\) indica que a quarta mulher avaliada no estudo tem dois filhos.

1.6 Somatório

A soma de \(n\) números \(x_1, x_2, ..., x_n\) é representada por \(\sum_{i=1}^n {x_i} = x_1 + x_2 + \dotsb + x_n\), e lê-se ‘somatório de xis \(i\) de um até ene’.

Exemplo 1.2 (Número de passos) Suponha que foi anotado o ‘número de passos até a lixeira mais próxima’ na cidade de Porto Alegre em \(n = 6\) ocasiões, conforme Tabela a seguir.

\(x_{1}\) \(x_{2}\) \(x_{3}\) \(x_{4}\) \(x_{5}\) \(x_{6}\)
186 402 191 20 7 124
Esta tabela indica que na primeira ocasião foram caminhados 186 passos até localizar uma lixeira (representado por \(x_1=186\)), na segunda foram 402 passos (representado por \(x_2=402\)), e assim sucessivamente. Para calcular o total de passos caminhados, pode-se fazer \[\begin{equation} \sum_{i=1}^6 {x_i} = x_1 + x_2 + \dotsb + x_6 = 186+402+191+20+7+124 = 930 \tag{1.1} \end{equation}\] 
186+402+191+20+7+124            # R e RStudio são calculadoras
## [1] 930
x <- c(186,402,191,20,7,124)    # Pode-se criar um vetor e atribuir a x
sum(x)                          # Usando a função 'sum', apresentada na Equação (1.1)
## [1] 930
sum(x^2)                        # Soma dos quadrados, representada pela Equação (1.2)
## [1] 248506

A letra grega \(\sum\) é o sigma maiúsculo, conforme Seção 1.8.1. Em muitos casos a simbologia de somatório é simplificada, utilizando-se \(\sum\), \(\sum_{x}\) ou \(\sum_{i}\). A seguir estão alguns exemplos mais avançados de uso mais sofisticado do somatório, podendo ser omitidos em uma primeira leitura. \[\begin{equation} \sum_{i=1}^n x_{i}^2 = x_{1}^2 + x_{2}^2 + \ldots + x_{n}^2 \tag{1.2} \end{equation}\]

Exercício 1.3 Considere o banco de dados disponível no pacote coronavirus6 conforme código a seguir. 
library(coronavirus)    # chamando a biblioteca 'coronavirus'
# update_dataset(silence = FALSE)  # atualizando os dados
data(coronavirus)       # deixando o banco de dados disponível
dim(coronavirus)        # dimensões do banco de dados (linhas x colunas)
## [1] 219852      7
head(coronavirus)       # mostrando o início do banco de dados
##         date province     country  lat long      type cases
## 1 2020-01-22          Afghanistan 33.9 67.7 confirmed     0
## 2 2020-01-23          Afghanistan 33.9 67.7 confirmed     0
## 3 2020-01-24          Afghanistan 33.9 67.7 confirmed     0
## 4 2020-01-25          Afghanistan 33.9 67.7 confirmed     0
## 5 2020-01-26          Afghanistan 33.9 67.7 confirmed     0
## 6 2020-01-27          Afghanistan 33.9 67.7 confirmed     0

a. Obtenha a soma de casos (cases) registrados ao longo de todo o período.
b. Obtenha a soma ao quadrado de casos registrados ao longo de todo o período.
c. Obtenha a soma de casos registrados ao longo de todo o período dividido por tipo (type).
d. Considerando a variável \(X\): ‘número de casos registrados’ em nrow(coronavirus) linhas do banco de dados, represente os itens a. e b. utilizando a notação de somatório.

1.7 Arredondamento e Truncagem

Arredondamento7 e truncagem são métodos para escrever números com precisão delimitada.

Para arredondar um número para a \(k\)-ésima casa decimal, basta observar a \(k\)+1-ésima casa. Se a \(k\)+1-ésima casa decimal for 0, 1, 2, 3 ou 4, mantém-se a \(k\)-ésima casa decimal; se a \(k\)+1-ésima casa decimal for 5, 6, 7, 8 ou 9, soma-se 1 à \(k\)-ésima casa decimal. Como exercício, releia a frase anterior substituindo ‘\(k\)-ésima’ por ‘primeira’ e ‘\(k\)+1-ésima’ por ‘segunda’, aplicando esta regra para o número 153.654321. Note que deve-se sempre avaliar o número original para realizar o arredondamento. Arredondamentos são comuns, por exemplo, ao calcularmos um índice de preço ou um montante de pagamento sobre o qual incidiu certa taxa de juros.

Para truncar um número para a \(k\)-ésima casa decimal, basta eliminar a \(k\)+1-ésima casa decimal e suas subsequentes. Como exercício, releia a frase anterior substituindo ‘\(k\)-ésima’ por ‘primeira’ e ‘\(k\)+1-ésima’ por ‘segunda’, aplicando esta regra novamente para o número 153.654321. Compare com os valores arredondados e note que pode-se utilizar números já truncados para continuar a reduzir a precisão sem a necessidade de conhecer o valor original. Truncagens são comuns, por exemplo, para representar idades e ao calcular os graus G1 e G2 da PUCRS. Assim, se o cálculo do seu G1 resultar em 6.99999999, o sistema irá truncar para 6.9, e não arredondar para 7.0.

Exemplo 1.3 (Arredondamento e truncagem)

Decimais Arredondamento Truncagem
6 153.654321 153.654321
5 153.65432 153.65432
4 153.6543 153.6543
3 153.654 153.654
2 153.65 153.65
1 153.7 153.6
0 154 153
-1 150 150
-2 200 100 
# Usando base R
options(digits = 10)            # Ajustando para apresentação de 10 dígitos (padrão: 7)
for(i in 6:-2){ print(round(153.654321, dig = i)) }        # 'digits' casas decimais
## [1] 153.654321
## [1] 153.65432
## [1] 153.6543
## [1] 153.654
## [1] 153.65
## [1] 153.7
## [1] 154
## [1] 150
## [1] 200
trunc <- function(x, ..., dig = 0) base::trunc(x*10^dig, ...)/10^dig   # Aprimorando
for(i in 6:-2){ print(trunc(153.654321, dig = i)) }        # Precisão de i decimais
## [1] 153.654321
## [1] 153.65432
## [1] 153.6543
## [1] 153.654
## [1] 153.65
## [1] 153.6
## [1] 153
## [1] 150
## [1] 100
# Usando o pacote plyr
plyr::round_any(153.654321, .01, round)           # dig = 2 em round
## [1] 153.65
plyr::round_any(153.654321, .0001, floor)         # dig = 4 em trunc
## [1] 153.6543
plyr::round_any(153.654321, 1, round)             # dig = 0 em round
## [1] 154
plyr::round_any(153.654321, 100, round)           # dig = -2 em round
## [1] 200

1.8 Outros símbolos e expressões

  • \(\sim\): tem distribuição.
  • \(\approx\): aproximadamente.
  • #: número de.
  • \(\pm\)/\(\mp\): mais ou menos/menos ou mais.
  • \(\bigtriangleup\): fim do Teorema.
  • i.e.: id est, expressão em Latim que significa ‘isto é’.
  • e.g.: exempli gratia, expressão em Latim que significa ‘por exemplo’.

1.8.1 Alfabeto grego

Maiúscula Minúscula Nome Maiúscula Minúscula Nome
\(A\) \(\alpha\) Alfa \(N\) \(\nu\) Nü
\(B\) \(\beta\) Beta \(\Xi\) \(\xi\) Csi
\(\Gamma\) \(\gamma\) Gama \(O\) \(o\) Ômicron
\(\Delta\) \(\delta\) Delta \(\Pi\) \(\pi\), \(\varpi\) Pi
\(E\) \(\epsilon\), \(\varepsilon\) Épsilon \(P\) \(\rho\), \(\varrho\) Rô
\(Z\) \(\zeta\) Zeta \(\Sigma\) \(\sigma\), \(\varsigma\) Sigma
\(H\) \(\eta\) Eta \(T\) \(\tau\) Tau
\(\Theta\) \(\theta\), \(\vartheta\) Teta \(\Upsilon\) \(\upsilon\) Úpsilon
\(I\) \(\iota\) Iota \(\Phi\) \(\phi\), \(\varphi\) Fi
\(K\) \(\kappa\), \(\varkappa\) Capa \(X\) \(\chi\) Qui
\(\Lambda\) \(\lambda\) Lambda \(\Psi\) \(\psi\) Psi
\(M\) \(\mu\) Mü \(\Omega\) \(\omega\) Ômega

  1. A Licença Pública Geral GNU é um tipo de licença utilizada para software livre, que garante aos usuários finais (indivíduos, organizações ou empresas) a liberdade de usar, estudar, compartilhar e modificar o software.↩︎

  2. Segundo a informação oficial, ‘é uma organização sem fins lucrativos com a missão de oferecer uma educação gratuita de alta qualidade para qualquer pessoa, em qualquer lugar’.↩︎

  3. Johns Hopkins University Center for Systems Science and Engineering (JHU CCSE). https://systems.jhu.edu/research/public-health/ncov↩︎

  4. Esta é a regra do arredondamento para o número mais próximo.↩︎