Capítulo 3 Probabilidade
Muito há para se falar sobre probabilidade desde a troca de correspondências entre Pascal e Fermat em 1654. Segundo Pierre-Simon Laplace15, ‘a teoria das probabilidades é, basicamente, o senso comum reduzido ao cálculo.’ Para o matemático italiano Bruno de Finetti16, ‘PROBABILIDADE NÃO EXISTE’. Neste material serão utilizadas as noções axiomática, subjetiva e frequentista de probabilidade, descritas em detalhes na Seção 2.2 de (Press 2003).
3.1 Propriedades
3.1.1 Propriedades fundamentais (Axiomas de Kolmogorov)
Um leitor mais atento pode perceber que foi feita uma combinação entre os axiomas de Kolmolgorov e as propriedades que são consequências destes axiomas. Tal abordagem tem por finalidade simplificar o entendimento neste curso de nível introdutório. Para maiores detalhes, recomenda-se (James 2010).
- P1
\[\begin{equation} 0 \le Pr(A) \le 1 \tag{3.1} \end{equation}\] - P2
\[\begin{equation} Pr(\Omega)=1 \tag{3.2} \end{equation}\] - P3 Se \(A_1\), \(A_2\), …, \(A_k\) são conjuntos disjuntos, então \[\begin{equation} Pr(A_1 \cup A_2 \cup \ldots \cup A_k) = Pr(A_1) + Pr(A_2) + \ldots + Pr(A_k) \tag{3.3} \end{equation}\]
3.1.2 Propriedades secundárias
Das propriedades fundamentais resultam outras, apresentadas sem demonstração:
P4
\[\begin{equation} Pr(A)=1-Pr(A^c) \tag{3.4} \end{equation}\]P5
\[\begin{equation} Pr(\emptyset)=0 \tag{3.5} \end{equation}\]P6
Se \(A_1\) e \(A_2\) são dois conjuntos quaisquer, então \[\begin{equation} Pr(A \cup B) = Pr(A) + Pr(B) - Pr(A \cap B) \tag{3.6} \end{equation}\]P7
\[\begin{equation} Pr(\left[ A \cup B \right]^c) = Pr(A^c \cap B^c) \tag{3.7} \end{equation}\]P8
\[\begin{equation} Pr(\left[ A \cap B \right]^c) = Pr(A^c \cup B^c) \tag{3.8} \end{equation}\]
3.2 R como um conjunto de tabelas estatísticas
(Venables et al. 2020) apontam que um uso conveniente de R é fornecer um conjunto abrangente de tabelas estatísticas. Funções são fornecidas para avaliar a função densidade de probabilidade (FDP) \(f(x)\), a função distribuição acumulada (FDA) \(F(x) = Pr(X \le x)\), a função quantil (dado \(q\), o menor \(x\) tal que \(Pr(X \le x) > q\)) e também para simular valores das distribuições. Utiliza-se o prefixo d para a densidade, p para o FDA, q para a função de quantil e r para simulação pseudo-aleatória. A seguir são apresentadas as distribuições de probabilidade disponíveis no base R. Para mais distribuições podem-se utilizar os pacotes adicionais mvtnorm (normal e t multivariadas) e VGAM (Dirichlet, multinomial, beta-binomial, entre outras).

3.3 Distribuição Normal
3.3.1 Normal univariada
A distribuição normal univariada é dada pela expressão
\(f(x|\mu, \sigma) = \dfrac{1}{\sqrt{2\pi} \sigma} \exp \bigg\{ -\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right) ^2 \bigg\}\)
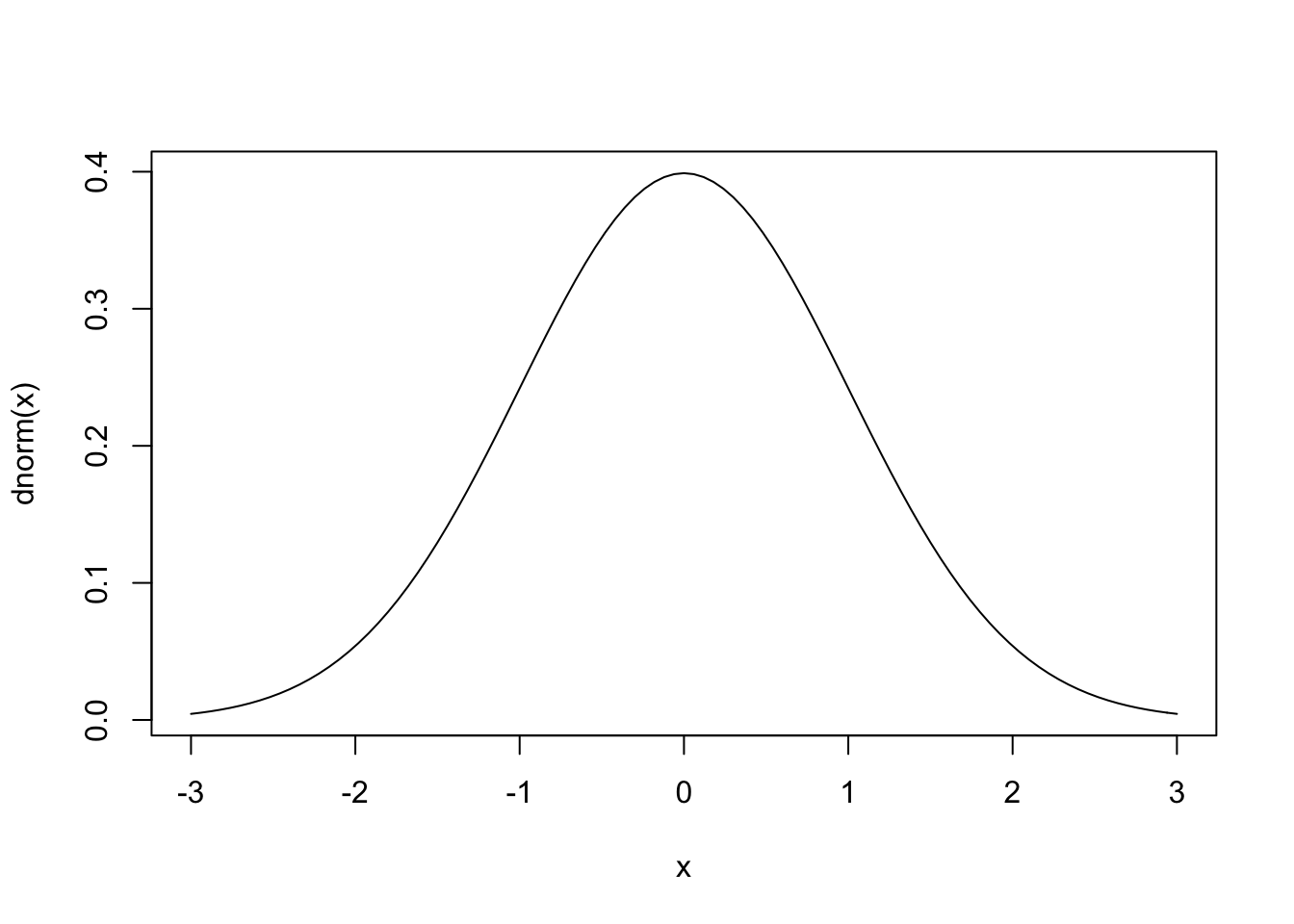
## [1] 0.5## [1] 0.95## [1] 0.975## [1] 0## [1] 1.64## [1] 1.963.3.2 Normal bivariada
No caso bivariado pode-se definir
\(f(x_1,x_2|\mu_1, \mu_2, \sigma_1, \sigma_2, \rho) = \dfrac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \exp \bigg\{ -\frac{1}{2(1-\rho^2)} \left[ \frac{(x_1-\mu_1)^2}{\sigma^2_1} + \frac{(x_2-\mu_2)^2}{\sigma^2_2} - \frac{2 \rho (x_1 - \mu_1) (x_2 - \mu_2)}{\sigma_1 \sigma_2} \right] \bigg\}.\)
library(rgl)
# parâmetros
n <- 100
x1 <- seq(-5, 5, length = n)
x2 <- seq(-5, 5, length = n)
m1 <- 0
m2 <- 0
s1 <- 1 # desvio padrão
s2 <- 2
# produto de normais independentes, \rho = 0
z1 <- outer(x1, x2, function(x,y) dnorm(x,m1,s1) * dnorm(y,m2,s2))
# gráficos
persp3d(x1, x2, z1, col = 'gray')
rglwidget()library(rgl)
library(mvtnorm)
# parâmetros
n <- 100
x1 <- seq(-5, 5, length = n)
x2 <- seq(-5, 5, length = n)
m1 <- 0
m2 <- 0
s1 <- 1^2 # variância
s2 <- 2^2
# via mvtnorm::dmvnorm, \rho = 0
m <- c(m1,m2)
s <- diag(c(s1,s2))
z2 <- outer(x1, x2, function(x,y) dmvnorm(cbind(x,y), mean = m, sigma = s))
# gráficos
persp3d(x1, x2, z2, col = 'lightblue')
rglwidget()library(rgl)
library(mvtnorm)
# parâmetros
n <- 100
x1 <- seq(-5, 5, length = n)
x2 <- seq(-5, 5, length = n)
m1 <- 0
m2 <- 0
s1 <- 1^2
s2 <- 2^2
r <- 0.9
# via mvtnorm::dmvnorm, \rho = 0.9
m <- c(m1,m2)
s <- matrix(c(s1,r,r,s2), nrow = 2, byrow = T)
z3 <- outer(x1, x2, function(x,y) dmvnorm(cbind(x,y), mean = m, sigma = s))
# gráficos
persp3d(x1, x2, z3, col = 'lightgreen')
rglwidget()As probabilidades podem ser calculadas através da função pmvnorm do pacote mvtnorm.
library(mvtnorm)
# parâmetros
m <- c(0,0)
s <- diag(2)
# Pr(X1 < 0, X2 < 0)
lower <- c(-Inf, -Inf)
upper <- c(0, 0)
pmvnorm(lower, upper, m, s)## [1] 0.25
## attr(,"error")
## [1] 1e-15
## attr(,"msg")
## [1] "Normal Completion"3.3.3 Normal multivariada
Para o caso multivariado define-se
\(f(\boldsymbol{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) = \dfrac{1}{\sqrt{2\pi} |\boldsymbol{\Sigma}|^{1/2}} \exp \bigg\{ -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})' \boldsymbol{\Sigma}^{1/2} (\boldsymbol{x} - \boldsymbol{\mu}) \bigg\}\),
\(\boldsymbol{\mu} = (\mu_1,\mu_2, \ldots, \mu_p)'\), \(\boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{1}^2 & \sigma_{12} & \cdots & \sigma_{1p} \\ \sigma_{12} & \sigma_{2}^2 & \cdots & \sigma_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{1p} & \sigma_{2p} & \cdots & \sigma_{p}^2 \end{bmatrix}\).
Referências
James, B. R. 2010. “Probabilidade: Um Curso Em Nível Intermediário, Coleção Euclides.” Rio de Janeiro. IMPA, 3a. Edição. https://loja.sbm.org.br/index.php/colecoes/impa/colecao-projeto-euclides/probabilidade-um-curso-em-nivel-intermediario.html.
Press, S James. 2003. Subjective and Objective Bayesian Statistics: Principles, Models, and Applications, 2nd. Edition. John Wiley & Sons. http://primo-pmtna01.hosted.exlibrisgroup.com/PUC01:PUC01:oclc(OCoLC)587388980.
Venables, William N, David M Smith, R Development Core Team, and others. 2020. “An Introduction to R.” Citeseer. https://cran.r-project.org/doc/manuals/r-release/R-intro.pdf.