5.8 Point estimation

• Section 3.2 from (Paulino, Turkman, and Murteira 2003)
  
• Sections 8.2 e 8.3 from (S. J. Press 2003)
  

Example 5.8 Considering the data from Example 5.6 and a prior \(Beta(1,1)\), one can calculate the point estimates of the posterior \(Beta(10,4)\) using the Equations (3.92), (3.94) and (3.95).

# If \theta ~ Beta(1,1), \theta|x ~ Beta(1+s,1+f)
s <- 9
f <- 3

(EX = (s+1)/(s+1+f+1))          # Mean (red)

## [1] 0.7142857

(MEX = (s+1-1/3)/(s+1+f+1-2/3)) # Median (blue)

## [1] 0.725

(MOX = (s+1-1)/(s+1+f+1-2))     # Mode (green)

## [1] 0.75

curve(dbeta(x, s+1,f+1))
abline(v = EX, col = 'red')
abline(v = MEX, col = 'blue')
abline(v = MOX, col = 'green')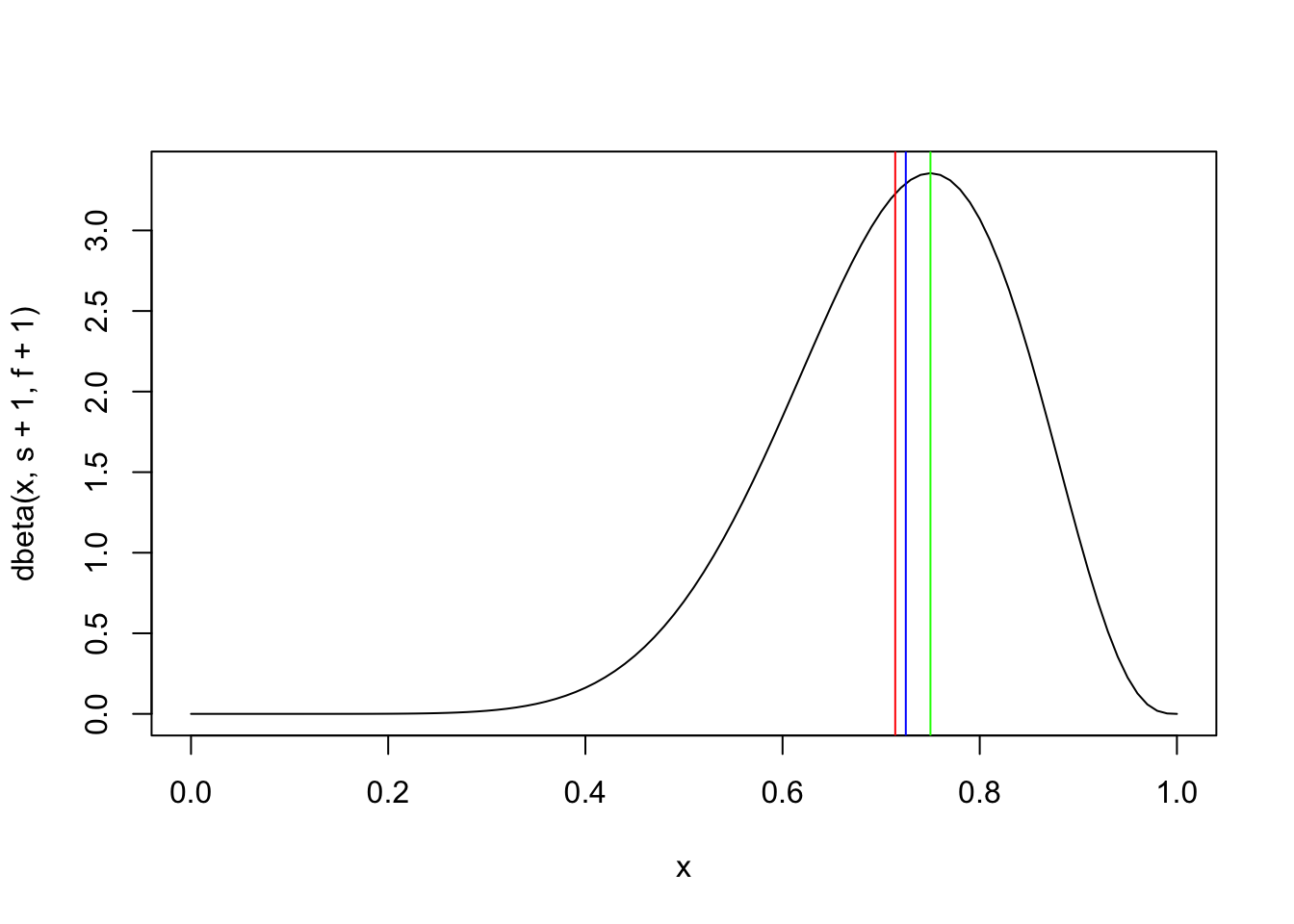

References

Paulino, Carlos Daniel Mimoso, Maria Antónia Amaral Turkman, and Bento Murteira. 2003. Estatı́stica Bayesiana. Fundação Calouste Gulbenkian, Lisboa. http://primo-pmtna01.hosted.exlibrisgroup.com/PUC01:PUC01:puc01000334509.

Press, S James. 2003. Subjective and Objective Bayesian Statistics: Principles, Models, and Applications, 2nd. Edition. John Wiley & Sons. http://primo-pmtna01.hosted.exlibrisgroup.com/PUC01:PUC01:oclc(OCoLC)587388980.