4.3 Amostra

Definição 4.9 Amostra é qualquer sequência de \(n\) unidades de \(\mathcal{U} = \lbrace 1, 2, \ldots, N \rbrace\), formalmente denotada por \(\boldsymbol{a} = (a_1,\ldots,a_n),\) tal que \(a_i \in \mathcal{U}\).

Exemplo 4.12 Os vetores \(\boldsymbol{a}_A = (2,3)\), \(\boldsymbol{a}_B = (3,3,1)\), \(\boldsymbol{a}_C = (2)\), \(\boldsymbol{a}_D = (2,2,3,3,1)\) são possíveis amostras de \(\mathcal{U} = \lbrace 1, 2, 3 \rbrace\).

Exemplo 4.13 No Exemplo 4.12, note os tamanhos de amostra \(n_A = n(\boldsymbol{a}_A) = 2\), \(n_B = n(\boldsymbol{a}_B) = 3\), \(n_C = n(\boldsymbol{a}_C) = 1\) e \(n_D = n(\boldsymbol{a}_D) = 5\).

Definição 4.10 Seja \(\mathcal{A}(\mathcal{U}) \equiv \mathcal{A}\), o conjunto de todas as amostras de \(\mathcal{U}\), de qualquer tamanho, e \(\mathcal{A}_{n}(\mathcal{U}) \equiv \mathcal{A}_{n}\) a subclasse de todas as amostras de tamanho \(n\).

Exemplo 4.14 Se \(\mathcal{U} = \lbrace 1, 2, 3 \rbrace\), \[\mathcal{A}(\mathcal{U}) = \lbrace (1),(2),(3),(1,1),(1,2),(1,3),(2,1),\ldots,(3,1,2,2,1),\ldots \rbrace,\] \[\mathcal{A}_{1}(\mathcal{U}) = \lbrace (1),(2),(3) \rbrace, \] \[\mathcal{A}_{2}(\mathcal{U}) = \lbrace (1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3) \rbrace. \] Simplificadamente \[\mathcal{A} = \lbrace 1,2,3,11,12,13,21,\ldots,31221,\ldots \rbrace,\] \[\mathcal{A}_{1} = \lbrace 1,2,3 \rbrace, \] \[\mathcal{A}_{2} = \lbrace 11,12,13,21,22,23,31,32,33 \rbrace. \]

Exemplo 4.15 No exemplo anterior, note o número de elementos (cardinalidade) de cada conjunto: \[|\mathcal{U}|=3\] \[|\mathcal{A}(\mathcal{U})| = \infty\] \[|\mathcal{A}_{1}(\mathcal{U})| = 3^1 = 3\] \[|\mathcal{A}_{2}(\mathcal{U})| = 3^2 = 9\] \[\vdots\] \[|\mathcal{A}_{n}(\mathcal{U})| = |\mathcal{U}|^n.\]

4.3.1 Plano Amostral

Definição 4.11 Um plano amostral (ordenado) é uma função \(P(\boldsymbol{a})\) definida em \(\mathcal{A}(\mathcal{U})\) satisfazendo \[P(\boldsymbol{a}) \ge 0, \; \forall \boldsymbol{a} \in \mathcal{A}(\mathcal{U}),\] tal que \[\sum_{\boldsymbol{a} \in \mathcal{A}} P(\boldsymbol{a}) = 1.\]

Exemplo 4.16 Considere \(\mathcal{U} = \lbrace 1, 2, 3 \rbrace\) e \(\mathcal{A}(\mathcal{U})\) conforme Exemplo 4.14. É possivel criar infinitos planos amostrais, tais como:

Plano A \(\cdot\) Amostragem Aleatória Simples com reposição (AASc) \[P(11)=P(12)=P(13)=1/9\] \[P(21)=P(22)=P(23)=1/9\] \[P(31)=P(32)=P(33)=1/9\]
Plano B \(\cdot\) Amostragem Aleatória Simples sem reposição (AASs) \[P(12)=P(13)=1/6\] \[P(21)=P(23)=1/6\] \[P(31)=P(32)=1/6\]
Plano C \(\cdot\) Combinações \[P(12)=P(13)=P(23)=1/3\]
Plano D \[P(3)=9/27\] \[P(12)=P(23)=3/27\] \[P(111)=P(112)=P(113)=P(123)=1/27\] \[P(221)=P(222)=P(223)=P(231)=1/27\] \[P(331)=P(332)=P(333)=P(312)=1/27\]

Exemplo 4.17 Considere a amostra \(\boldsymbol{a} = (1,2)\) obtida do universo do Exemplo 4.4 a partir de algum plano amostral válido. \[\boldsymbol{x} = (\boldsymbol{x}_1,\boldsymbol{x}_2) = \left( \begin{bmatrix} 24 \\ 1.66 \\ F \end{bmatrix}, \begin{bmatrix} 32 \\ 1.81 \\ M \end{bmatrix} \right) = \left( \begin{array}{cc} 24 & 32 \\ 1.66 & 1.81 \\ F & M \end{array} \right).\]

Definição 4.12 Uma estatística é uma função dos dados amostra \(\boldsymbol{a}\) anotada por \(h(\boldsymbol{x})\).

Exemplo 4.18 Considere \(\boldsymbol{x}\), a matriz dos dados da amostra \(\boldsymbol{a} = (1,2)\). São exemplos de estatísticas: \[h_1 = \frac{24+32}{2} = 28 \;\;\;\;\; \textrm{(média das idades)}\] \[h_2 = \frac{1.66+1.81}{2} = 1.735 \;\;\;\;\; \textrm{(média das alturas)}\] \[h_3 = 32-24 = 8 \;\;\;\;\; \textrm{(amplitude das idades)}\] \[h_4 = \sqrt{24^2+32^2} = \sqrt{1600} = 40 \;\;\;\;\; \textrm{(norma das idades)}\] \[h_5 = \frac{1+0}{2} = \frac{1}{2} \;\;\;\;\; \textrm{(proporção de mulheres)}\]

Exercício 4.4 Calcule as estatísticas do Exemplo 4.18 considerando as amostras \(\boldsymbol{a} = (1,3)\) e \(\boldsymbol{a} = (2,3)\).

4.3.2 Distribuições amostrais

Definição 4.13 A distribuição amostral de uma estatística \(h(\boldsymbol{x})\) segundo um plano amostral \(\lambda\), é a distribuição de probabilidades \(H(\boldsymbol{x})\) definida sobre \(\mathcal{A}_\lambda\), com função de probabilidade \[p_h = P_\lambda(H(\boldsymbol{x})=h) = P(h) = \frac{f_h}{|\mathcal{A}_\lambda|}.\]

Exemplo 4.19 Considere a variável idade do Exemplo 4.4 e as estatísticas \(h_1(\boldsymbol{x})=\frac{1}{n}\sum_{i=1}^n x_i\) e \(h_2(\boldsymbol{x})=\frac{1}{n-1}\sum_{i=1}^n (x_i-h_1(\boldsymbol{x}))^2\) aplicadas sobre o plano amostral A do Exemplo 4.16. Note que \(h_1(\boldsymbol{x})\) e \(h_2(\boldsymbol{x})\) são respectivamente a média (Eq. (2.14)) e a variância (Eqs. (2.32) e (2.33)) amostrais.

Plano A \(\cdot\) Amostragem Aleatória Simples com reposição (AASc)

\(i\)	1	2	3	4	5	6	7	8	9
\(\boldsymbol{a}\)	11	12	13	21	22	23	31	32	33
\(P(\boldsymbol{a})\)	1/9	1/9	1/9	1/9	1/9	1/9	1/9	1/9	1/9
\(\boldsymbol{x}\)	(24,24)	(24,32)	(24,49)	(32,24)	(32,32)	(32,49)	(49,24)	(49,32)	(49,49)
\(h_1(\boldsymbol{x})\)	24.0	28.0	36.5	28.0	32.0	40.5	36.5	40.5	49.0
\(h_2(\boldsymbol{x})\)	0.0	32.0	312.5	32.0	0.0	144.5	312.5	144.5	0.0

\(h_1\)	24.0	28.0	32.0	36.5	40.5	49.0	Total
\(f_{h1}\)	1	2	1	2	2	1	9
\(p_{h1}\)	1/9	2/9	1/9	2/9	2/9	1/9	1

\(h_2\)	0.0	32.0	144.5	312.5	Total
\(f_{h2}\)	3	2	2	2	9
\(p_{h2}\)	3/9	2/9	2/9	2/9	1

Exemplo 4.20 Considere novamente a variável idade do Exemplo 4.4 e a estatística \(h_1(\boldsymbol{x})=\frac{1}{n}\sum_{i=1}^n x_i\), agora aplicada sobre o plano amostral B do Exemplo 4.16.

Plano B \(\cdot\) Amostragem Aleatória Simples sem reposição (AASs)

\(i\)	1	2	3	4	5	6
\(\boldsymbol{a}\)	12	13	21	23	31	32
\(P(\boldsymbol{a})\)	1/6	1/6	1/6	1/6	1/6	1/6
\(\boldsymbol{x}\)	(24,32)	(24,49)	(32,24)	(32,49)	(49,24)	(49,32)
\(h_1(\boldsymbol{x})\)	28.0	36.5	28.0	40.5	36.5	40.5

\(h_1\)	28.0	36.5	40.5	Total
\(f_{h1}\)	2	2	2	6
\(p_{h1}\)	2/6	2/6	2/6	1

Exemplo 4.21 Considere novamente a variável idade do Exemplo 4.4 e a estatística \(h_1(\boldsymbol{x})=\frac{1}{n}\sum_{i=1}^n x_i\), agora aplicada sobre o plano amostral C do Exemplo 4.16.

Plano C \(\cdot\) Combinações

\(i\)	1	2	3
\(\boldsymbol{a}\)	12	13	23
\(P(\boldsymbol{a})\)	1/3	1/3	1/3
\(\boldsymbol{x}\)	(24,32)	(24,49)	(32,49)
\(h_1(\boldsymbol{x})\)	28.0	36.5	40.5

\(h_1\)	28.0	36.5	40.5	Total
\(f_{h1}\)	1	1	1	3
\(p_{h1}\)	1/3	1/3	1/3	1

Exercício 4.5 Refaça os Exemplos 4.19, 4.20 e 4.21 considerando a variável altura. Para os Exemplos 4.20 e 4.21, calcule também a estatística \(h_2(\boldsymbol{x})=\frac{1}{n-1}\sum_{i=1}^n (x_i-h_1(\boldsymbol{x}))^2\).

Exemplo 4.22 A seguir são implementadas em R as resoluções dos Exemplos 4.19 e 4.20.

U <- 1:3                    # universo
(aasc <- expand.grid(U,U))  # AASc de tamanho n=2

##   Var1 Var2
## 1    1    1
## 2    2    1
## 3    3    1
## 4    1    2
## 5    2    2
## 6    3    2
## 7    1    3
## 8    2    3
## 9    3    3

(aasc <- cbind(aasc[,2],aasc[,1])) # trocando as colunas

##       [,1] [,2]
##  [1,]    1    1
##  [2,]    1    2
##  [3,]    1    3
##  [4,]    2    1
##  [5,]    2    2
##  [6,]    2    3
##  [7,]    3    1
##  [8,]    3    2
##  [9,]    3    3

(aass <- aasc[-c(1,5,9),])  # AASs de tamanho n=2

##      [,1] [,2]
## [1,]    1    2
## [2,]    1    3
## [3,]    2    1
## [4,]    2    3
## [5,]    3    1
## [6,]    3    2

x1 <- c(24,32,49)           # dados de idade
n <- ncol(aasc)
# AASc
(xc <- cbind(x1[aasc[,1]], x1[aasc[,2]]))

##       [,1] [,2]
##  [1,]   24   24
##  [2,]   24   32
##  [3,]   24   49
##  [4,]   32   24
##  [5,]   32   32
##  [6,]   32   49
##  [7,]   49   24
##  [8,]   49   32
##  [9,]   49   49

(mxc <- rowMeans(xc))       # estatística h1(x) aplicada na AASc

## [1] 24.0 28.0 36.5 28.0 32.0 40.5 36.5 40.5 49.0

(tabc <- table(mxc))        # frequência amostral de h1(x)

## mxc
##   24   28   32 36.5 40.5   49 
##    1    2    1    2    2    1

MASS::fractions(prop.table(tabc)) # distribuição amostral de h1(x)

## mxc
##   24   28   32 36.5 40.5   49 
##  1/9  2/9  1/9  2/9  2/9  1/9

# vyc <- (rowMeans(xc^2)-mxc^2)*(n/(n-1))
# AASs
(xs <- cbind(x1[aass[,1]], x1[aass[,2]]))

##      [,1] [,2]
## [1,]   24   32
## [2,]   24   49
## [3,]   32   24
## [4,]   32   49
## [5,]   49   24
## [6,]   49   32

(mxs <- rowMeans(xs))       # estatística h(x) aplicada na AASs

## [1] 28.0 36.5 28.0 40.5 36.5 40.5

(tabs <- table(mxs))        # frequência amostral de h(x)

## mxs
##   28 36.5 40.5 
##    2    2    2

MASS::fractions(prop.table(tabs)) # distribuição amostral de h(x)

## mxs
##   28 36.5 40.5 
##  1/3  1/3  1/3

Exemplo 4.23 Em Python.

import numpy as np
import pandas as pd
from fractions import Fraction

U = np.array([1, 2, 3])  # universo
x1 = np.array([24, 32, 49])  # dados de idade

# AASc de tamanho n=2
aasc = np.array(np.meshgrid(U, U)).T.reshape(-1, 2)
aasc = aasc[:, [1, 0]]  # trocando as colunas para melhor leitura

# AASs de tamanho n=2
aass = np.array([(i, j) for i in U for j in U if i != j])

n = aasc.shape[1]

# AASc
xc = np.array([x1[i - 1] for i in aasc.flatten()]).reshape(aasc.shape)
mxc = np.mean(xc, axis=1)
tabc = pd.Series(mxc).value_counts()
dist_amostral_aasc = tabc / len(mxc)
print("Distribuição amostral AASc:")
print(dist_amostral_aasc.apply(lambda x: Fraction(x).limit_denominator()))

# AASs
xs = np.array([x1[i - 1] for i in aass.flatten()]).reshape(aass.shape)
mxs = np.mean(xs, axis=1)
tabs = pd.Series(mxs).value_counts()
dist_amostral_aass = tabs / len(mxs)
print("\nDistribuição amostral AASs:")
print(dist_amostral_aass.apply(lambda x: Fraction(x).limit_denominator()))

Exemplo 4.24 As resoluçãos dos Exemplos 4.20 e 4.21 podem ser implementadas no pacote arrangements do R. Note que são obtidas as amostras via AASs através da função permutations e as amostras por combinação, sem qualquer tipo de repetição, pela função combinations.

library(arrangements)
x1 <- c(24,32,49)  # dados de idade
# AASs
npermutations(3,2) # número de amostras via AASs

## [1] 6

(aass <- arrangements::permutations(3,2)) # gerando as AASs

##      [,1] [,2]
## [1,]    1    2
## [2,]    1    3
## [3,]    2    1
## [4,]    2    3
## [5,]    3    1
## [6,]    3    2

(maass <- matrix(x1[t(aass)], ncol=2, byrow = T))

##      [,1] [,2]
## [1,]   24   32
## [2,]   24   49
## [3,]   32   24
## [4,]   32   49
## [5,]   49   24
## [6,]   49   32

rowMeans(maass)

## [1] 28.0 36.5 28.0 40.5 36.5 40.5

mean(rowMeans(maass)) # plano amostral não viesado

## [1] 35

# Combinações
ncombinations(3,2) # número de amostras via combinação

## [1] 3

(comb <- arrangements::combinations(3,2)) # amostras via combinação

##      [,1] [,2]
## [1,]    1    2
## [2,]    1    3
## [3,]    2    3

(mcomb <- matrix(x1[t(comb)], ncol=2, byrow = T))

##      [,1] [,2]
## [1,]   24   32
## [2,]   24   49
## [3,]   32   49

rowMeans(mcomb)

## [1] 28.0 36.5 40.5

mean(rowMeans(mcomb)) # plano amostral não viesado

## [1] 35

Exemplo 4.25 Em Python.

import numpy as np
from itertools import permutations, combinations

x1 = np.array([24, 32, 49])  # dados de idade

# AASs (permutações)
n_permutacoes = len(list(permutations(x1, 2)))
print(f"Número de amostras via AASs: {n_permutacoes}") # Output: 6

aass = np.array(list(permutations(x1, 2)))
maass = np.mean(aass, axis=1)
print(f"Médias das amostras AASs: {maass}")
print(f"Média das médias AASs: {np.mean(maass)}")  # Output: 35.0

# Combinações
n_combinacoes = len(list(combinations(x1, 2)))
print(f"\nNúmero de amostras via combinação: {n_combinacoes}")  # Output: 3

comb = np.array(list(combinations(x1, 2)))
mcomb = np.mean(comb, axis=1)
print(f"Médias das amostras combinação: {mcomb}")
print(f"Média das médias combinação: {np.mean(mcomb)}")  # Output: 31.67

Exercício 4.6 Generalize os Exemplos 4.22 e 4.21 para qualquer tamanho de amostra, parametrizando as opções com e sem reposição, bem como para combinações. Por fim, adicione um argumento que permita calcular qualquer estatística.

4.3.2.1 Distribuição amostral da média

Com base no Teorema Central do Limite descrito na Seção 3.9.3.1, sabe-se que a distribuição das médias amostrais de qualquer variável aleatória que satisfaça as condições do teorema converge para a distribuição normal. Considere \(X\) com distribuição \(\mathcal{D}\) qualquer, com média \(\mu\) e desvio padrão \(\sigma\), simbolizada por \[X \sim \mathcal{D}(\mu,\sigma).\] Pelo TCL, a distribuição das médias amostrais de qualqer tamanho \(n_0\) é tal que \[\bar{X}_{n_0} \sim \mathcal{N} \left( \mu,\frac{\sigma}{\sqrt{n_0}} \right).\] A medida \(\sigma/\sqrt{n_0}\) é conhecida como erro padrão (da média). O TCL é um resultado assintótico²⁸, portanto quanto mais próxima \(\mathcal{D}\) estiver de \(\mathcal{N}\), mais rápida deve ser a convergência de \(\bar{X}_{n_0}\) para a distribuição normal.

Exemplo 4.26 Considere a variável aleatória \(X\): QI da população mundial, admitida com distribuição normal de média \(\mu=100\) e desvio padrão de \(\sigma=15\), anotada por \(X \sim \mathcal{N}(100,15)\).

mu <- 100 # média de X
sigma <- 15  # desvio padrão de X
curve(dnorm(x, mean = mu, sd = sigma), # densidade
      from = mu-3*sigma, to = mu+3*sigma,
      main = 'X ~ N(100,15)')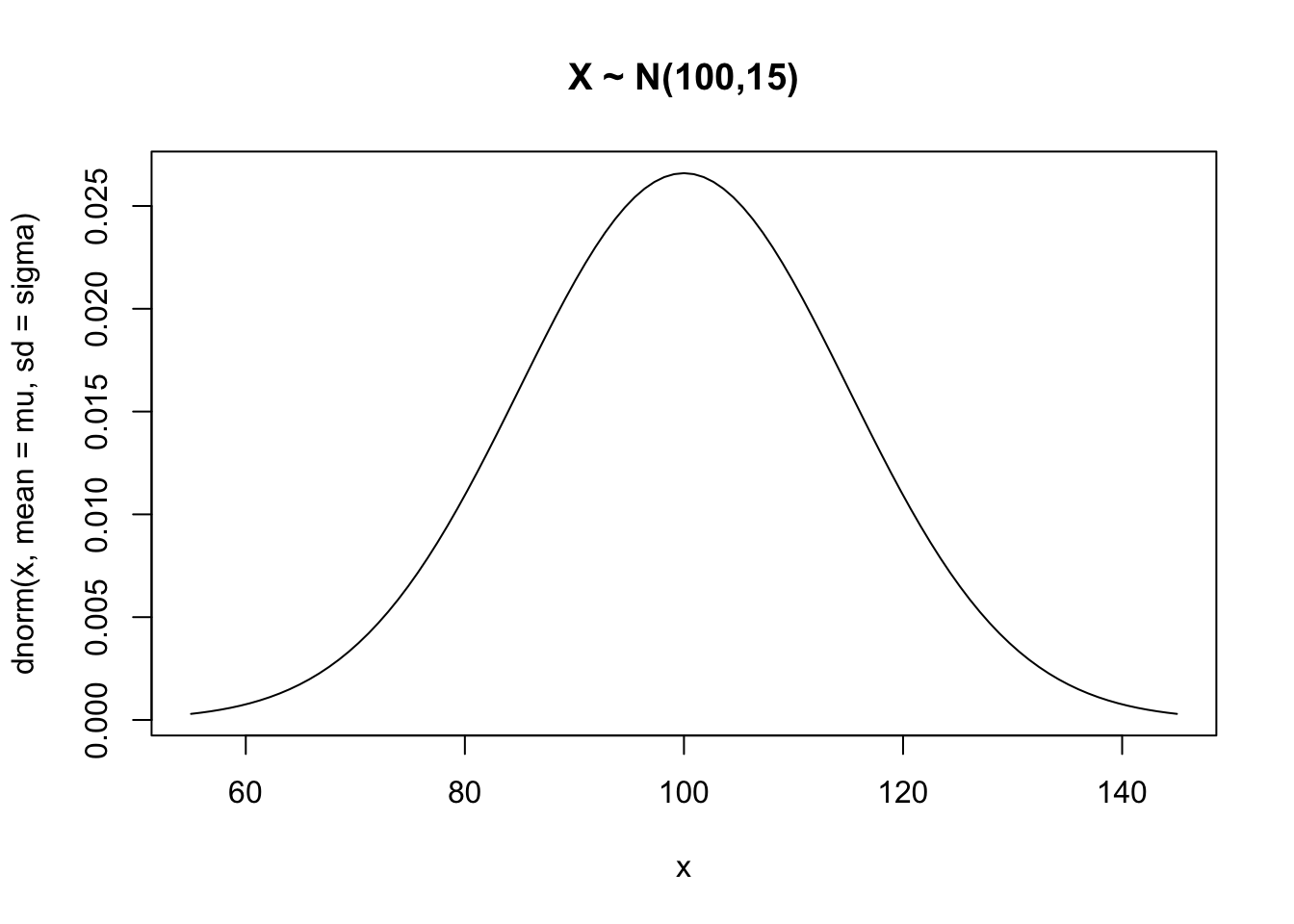

n0 <- 25 # tamanho das amostras
n <- 200 # número de amostras
set.seed(1234) # fixando semente aleatória para garantir replicação
a <- MASS::mvrnorm(n0, mu = rep(mu,n), Sigma = sigma^2*diag(n))
ma <- colMeans(a) # médias das n amostras
hist(ma) # histograma das médias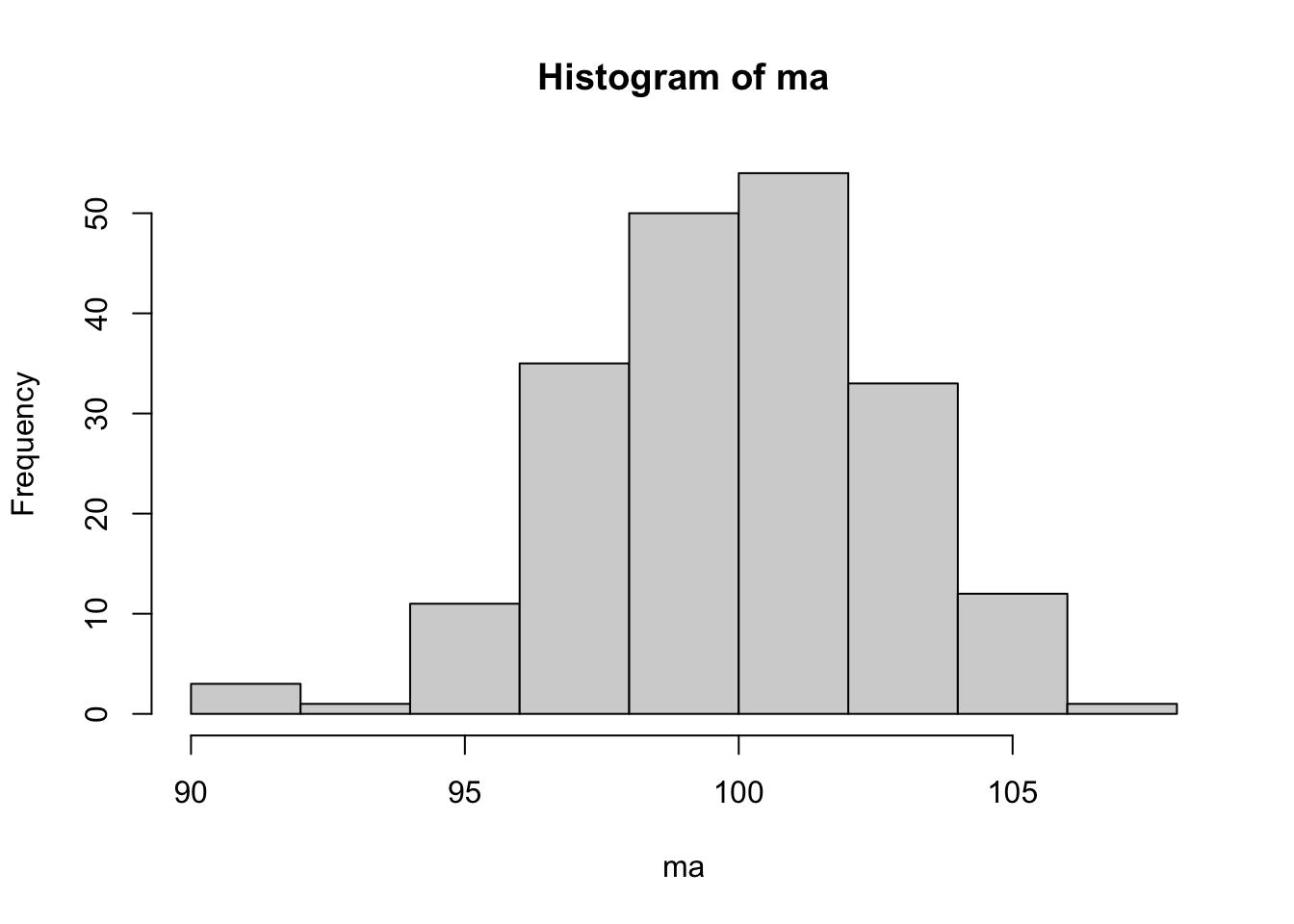

mean(ma) # média das médias amostrais, próxima de mu

## [1] 99.90468

sd(ma) # erro padrão das simulações, próximo de sigma/raiz(n0)

## [1] 2.817847

sigma/sqrt(n0) # sigma/raiz(n0), erro padrão teórico

## [1] 3

Exemplo 4.27 Em Python.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Parâmetros da distribuição normal
mu = 100  # média de X
sigma = 15  # desvio padrão de X

# Plotando a curva da distribuição normal
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.plot(x, norm.pdf(x, loc=mu, scale=sigma))
plt.title('Distribuição Normal N(100, 15)')
plt.xlabel('X')
plt.ylabel('Densidade')
plt.show()

# Gerando amostras aleatórias
n0 = 25  # tamanho das amostras
n = 200  # número de amostras
np.random.seed(1234)  # fixando a semente para reprodutibilidade
a = np.random.normal(loc=mu, scale=sigma, size=(n0, n))

# Calculando as médias das amostras
ma = np.mean(a, axis=0)  # médias das n amostras

# Densidade
plt.hist(ma, bins='auto', color='lightgray', edgecolor='black')
plt.title('Histograma das Médias Amostrais')
plt.xlabel('Média Amostral')
plt.ylabel('Frequência')
plt.show()

# Média das médias amostrais
print(f"Média das médias amostrais: {np.mean(ma):.4f}")

# Desvio padrão das médias amostrais (erro padrão das simulações)
print(f"Desvio padrão das médias amostrais: {np.std(ma):.4f}")

# Erro padrão teórico (sigma/sqrt(n0))
print(f"sigma/sqrt(n0): {sigma/np.sqrt(n0):.4f}")

Exercício 4.7 Refaça o Exemplo 4.26 alterando os valores de n0 e n, verificando o que ocorre no histograma, média e desvio padrão de ma. Atente para o fato de que valores de n maiores que 1000 podem tornar o processo custoso computacionalmente.

4.3.3 Amostra representativa

Ouve-se frequentemente o argumento de que uma boa amostra é aquela que é representativa. Indagado sobre a definição de uma amostra representativa, a resposta mais comum é algo como: “aquela que é uma micro representação do universo”. Mas para se ter certeza de que uma amostra seja uma micro representação do universo para uma dada característica de interesse, deve-se conhecer o comportamento dessa mesma característica da população. Então, o conhecimento da população seria tão grande que tonar-se-ia desnecessária a coleta da amostra.
(Bolfarine and Bussab 2005, 14)

Neste material o termo “representativo” será condicional. Por exemplo, “representativo considerando as proporções populacionais aproximadas das variáveis \(X_1, \ldots, X_n\)”.

4.3.4 Tipos de amostras

Tipos de amostras segundo (Jessen 1978) e (Bolfarine and Bussab 2005).

Critério	Procedimento de seleção
	Probabilístico	Não probabilístico
Objetivo	amostras probabilísticas	amostras criteriosas
Subjetivo	amostras quase-aleatórias	amostras intencionais

Procedimentos probabilísticos objetivos são mais bem aceitos academicamente, ainda que na prática nem sempre possam ser executados. Quando isso ocorre, podem-se considerar procedimentos que sejam possíveis de serem executados.

References

Bolfarine, Heleno, and Wilton de Oliveira Bussab. 2005. Elementos de Amostragem. Editora Blucher. https://www.blucher.com.br/livro/detalhes/elementos-de-amostragem-331.

Jessen, Raymond James. 1978. Statistical Survey Techniques. Wiley New York. https://archive.org/details/statisticalsurve00jess/mode/2up.

Um resultado assintótico é aquele que depende de uma ou mais variávies sendo observadas próximas a certos limites de referência.↩︎