6.3 Teste de Hipóteses

(Sheskin 2011) apresenta um compêndio detalhado dos testes de hipóteses clássicos.

6.3.1 Via intervalos de confiança

Os testes de hipóteses clássicos possuem as mesmas características e propriedades dos seus respectivos intervalos de confiança. Desta forma, apresenta-se um breve exemplo abordando a equivalência entre os TH e os IC para a proporção universal \(\pi\).

Exemplo 6.20 (TH \(\equiv\) IC) Suponha uma moeda com probabilidade de face cara \(P(H)=\pi\). Em princípio não sabemos o valor de \(\pi\), e pode ser interessante considerar duas configurações:

\[\left\{ \begin{array}{l} H_0: \mbox{a moeda é equilibrada}\\ H_1: \mbox{a moeda não é equilibrada}\\ \end{array} \right. \equiv \left\{ \begin{array}{l} H_0: \pi = 0.5 \\ H_1: \pi \ne 0.5 \\ \end{array} \right. \]

Aplicando a ideia de Charles Sanders Peirce de supor \(H_{0}\) verdadeira (sob \(H_{0}\)), espera-se observar ‘cara’ em 50% dos resultados, com alguma variação em torno de 50%. Considerando a Equação (6.8) pode-se obter a margem de erro esperada para esta oscilação em função do tamanho da amostra \(n\) para, digamos, 95% dos casos: \[ IC \left[ \pi, 95\% \right] = 0.5 \mp 1.96 \sqrt{\dfrac{0.5 \left(1-0.5\right)}{n}} = 0.5 \mp \dfrac{0.98}{\sqrt{n}} \]

Assim, ao realizar \(n=25\) lançamentos e observar uma frequência de caras no intervalo \[ IC \left[ \pi, 95\% \right] = 0.5 \mp \dfrac{0.98}{\sqrt{25}} = \left[ 0.304,0.696 \right] = \left[ 30.4\%,69.6\% \right] \] pode-se considerar a moeda equilibrada com \(1-\alpha=95\%\) de confiança. Caso a frequência seja inferior a \(30.4\%\) ou superior a \(69.6\%\), há indícios de que a moeda seja desequilibrada, também com 95% de confiança. Pela terminologia dos testes de hipóteses, não se rejeita \(H_{0}\) com \(\alpha=5\%\). Se \(n=100\), \[ IC \left[ \pi, 95\% \right] = 0.5 \mp \dfrac{0.98}{\sqrt{100}} = \left[ 0.402,0.598 \right] = \left[ 40.2\%,59.8\% \right] \] e obtém-se um intervalo menor se comparado a \(n=25\), i.e., mais preciso para a mesma confiança de 95%. Se Como exercício, use a função ic() para definir outros valores para \(n\) e teste este resultado em uma moeda.

# IC95% sob H0: \pi=0.5
ic <- function(n){
  cat('[', 0.5-.98/sqrt(n), ',',
           0.5+.98/sqrt(n), ']')
}
ic(25)

## [ 0.304 , 0.696 ]

ic(100)

## [ 0.402 , 0.598 ]

Exemplo 6.21 Em Python.

import numpy as np

def ic(n):
  """
  Calcula o IC de 95% para uma proporção sob H0: pi = 0.5.

  Args:
    n: Tamanho da amostra.
  """
  lower = 0.5 - 0.98 / np.sqrt(n)
  upper = 0.5 + 0.98 / np.sqrt(n)
  print(f"[{lower:.4f}, {upper:.4f}]")

# Calculando o IC para n = 25 e n = 100
ic(25)  # Output: [0.3040, 0.6960]
ic(100)  # Output: [0.4020, 0.5980]

6.3.2 Hipótese nula \(H_0\)

Considerando o espaço paramétrico descrito na Seção 5.9, a hipótese que envolve \(\Theta_0\) é chamada hipótese nula, e a que envolve \(\Theta_1\) é a hipótese alternativa. Tais hipóteses podem ser escritas na forma

\[\left\{ \begin{array}{l} H_0: \theta \in \Theta_0\\ H_1: \theta \in \Theta_1 \\ \end{array} \right. \]

Como mencionado, nos procedimentos de testes de hipóteses clássicos supõe-se inicialmente que \(H_0\) seja verdadeira. Por este motivo a hipótese nula sempre deve conter a igualdade, conforme indicado na Figura 6.1. Note que não há uma ‘regra da hipótese nula’, a indicação está colocada desta forma apenas por motivos didáticos.

Figura 6.1: Regra didático-pedagógica, sem respaldo na literatura

6.3.3 Hipótese alternativa \(H_1\)

As regras da Figura 6.1 implicam em três tipos de hipótese alternativa.

• Bilateral ou bicaudal testa uma hipótese de equilíbrio ou quando não há definição prévia sobre a direção da hipótese.
• Unilateral inferior ou unicaudal inferior verifica a hipótese que indica um piso de referência.
• Unilateral superior ou unicaudal superior avalia uma hipótese que indica um teto de referência

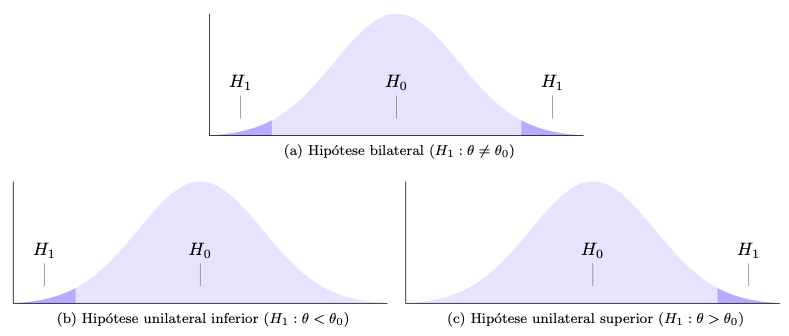
Figura 6.2: Tipos de hipótese

6.3.3.1 Definição das hipóteses estatísticas

1. Escreva \(\left\{ \begin{array}{l} H_0: \\ H_1: \end{array} \right.\)
2. Indique o parâmetro sendo testado.
3. Indique o valor teórico de referência.
4. Atribua as desigualdades das hipóteses.

Exercício 6.7 Para cada item abaixo, indique as hipóteses sendo testadas.

1. A companhia de transporte afirma que, em média, o intervalo entre sucessivos ônibus de uma determinada linha é de 15 minutos. Uma associação de usuários de transportes coletivos acha que a pontualidade é muito importante, e deseja testar a afirmação da companhia. Solução: 2. Parâmetro média \(\mu\), 3. Valor de referência 15 min., 4. ‘é de 15 minutos’ sugere \(\mu=15\), logo \(\left\{ \begin{array}{l} H_0: \mu=15 \\ H_1: \mu \ne 15 \end{array} \right.\).
2. Os amortecedores de automóveis que circulam em cidades duram pelo menos 100 mil quilômetros em média, segundo a informação de algumas oficinas especializadas. O proprietário de uma locadora de veículos deseja testar esta afirmação.
3. Um veterinário afirma ter obtido um ganho médio diário de pelo menos 3 litros de leite por vaca com uma nova composição de ração. Um pecuarista acredita que o ganho não é tão grande assim.
4. Algumas garrafas de cerveja declaram em seus rótulos conter 600mL. Os órgãos de fiscalização desejam avaliar se uma fábrica deve ou não ser autuada por engarrafar cervejas com uma quantidade menor que o indicado no rótulo.
5. O dado de um cassino parece estar viciado, saindo o valor 1 com uma frequência muito grande.
6. Um fabricante afirma que a sua vacina previne pelo menos 80% dos casos de uma doença. Um grupo de médicos desconfia que a vacina não é tão eficiente assim.

6.3.4 Estatística do teste

Sob \(H_0\) compara(m)-se o(s) valor(es) descrito(s) nesta hipótese com os dados da amostra através da estatística de teste. Caso a estatística do teste indique uma pequena distância entre o(s) valor(es) de \(H_0\) e os dados da amostra, admite-se ou não se rejeita \(H_0\); caso a distância seja grande, rejeita-se \(H_0\).

As distâncias que fazem admitir ou rejeitar \(H_0\) são avaliadas em termos probabilísticos, indicadas na Figura 6.2. A divisão destas regiões é dada por valores críticos, quantis das distribuições associadas que limitam a significância (\(\alpha\)), a área da região crítica ou região de rejeição.

6.3.5 Tipos de erro

O procedimento de teste de hipóteses clássico é baseado nos erros do tipo I e tipo II. A região crítica está associada à probabilidade de erro do tipo I.

• Erro do tipo I: errar ao rejeitar uma hipótese \(H_0\) verdadeira.
• Erro do tipo II: errar ao não rejeitar uma hipótese \(H_0\) falsa.

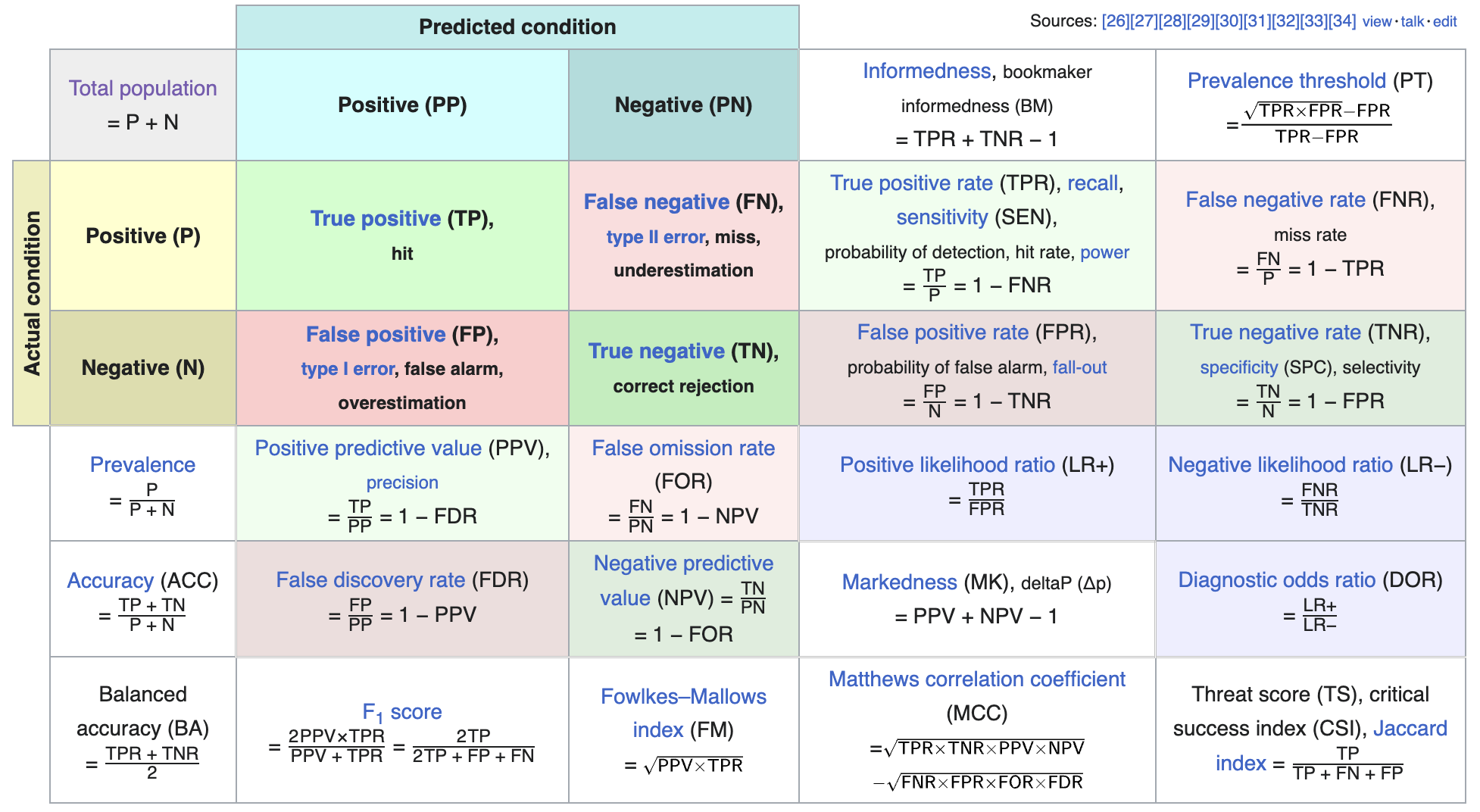
Figura 6.3: Tipos de erro conforme artigo Confusion matrix da Wikipedia

6.3.6 Valor-p

É possível considerar formas mais precisas de avaliar as distâncias probabilisticas das estatísticas de teste, ao invés apenas de indicar ‘acima’ ou ‘abaixo’ de um valor crítico. Pelo paradigma clássico, atribui-se uma medida que varia entre 0 e 1, chamada valor-p. Este medida possui múltiplas definições, bastante discutida e frequentemente mal interpretada. A definição a seguir é baseada na Definição 2.1 de (Carlos Alberto de Braganca Pereira and Wechsler 1993, 161).

Definição 6.2 Considere um experimento produzindo dados \(x\), uma observação de \(X\), para testar uma hipótese simples \(H_0\) versus \(H_1\). O valor-p é a probabilidade, sob \(H_0\), do evento composto por todos os pontos amostrais que favorecem \(H_1\) (contra \(H_0\)) serem tão o mais extremos do que \(x\).

Note que um um valor-p alto pode indicar ‘\(H_0\) é mais verossímil que \(H_1\)’ OU ‘não tenho informação para decidir entre \(H_0\) e \(H_1\)’. Este é o motivo do cuidado ao declarar ‘não se rejeita \(H_0\)’.

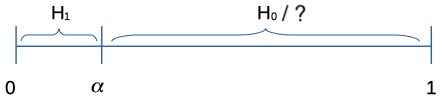
Figura 6.4: Regra de decisão via valor-p e \(\alpha\)

Tal valor de significância é arbitrário, ou seja, deve ser definido pelo decisor ao estipular quanto admite de probabilidade máxima de erro do tipo I. Existem valores de significância típicos, usualmente 10%, 5%, 1%, e 0.1%. Devido a um exemplo dado por (Ronald A. Fisher 1925, 44) ⁴³, o valor de 5% tornou-se uma referência para o valor de \(\alpha\). Uma sugestão para escapar desta arbitrariedade é combinar o valor-p com o fator de Bayes conforme discutido na Seção 5.9.4.

Exercício 6.8 Considere a imagem a seguir.

Figura 6.5: https://imgflip.com/i/5ejhg4

1. Comente a frase do meme.
2. Complete a frase: ‘If the p is high, …’.

Exercício 6.9 Acesse https://rpsychologist.com/pvalue/ e realize as simulações sugeridas.

Exemplo 6.22 (Momentinho Cultural) The P Value Song de Michael Greenacre & Gurdeep Stephens.

Statistics, logistics, cladistics seem to me
To have a common theme scientifically,
Economists, biologists, with PhD degrees,
They all need some proof of their theories.
A letter is the key, you’ll see clearly,
Not B nor G nor V – but it’s the P!

There’s no values like P-values
Like no values I know
Think of something that is not worth proving,
An hypothesis that everyone calls null,
If your P is too large to reject it
Then your experiment is rather dull.

There’s no values like P-values,
Especially when they are low,
Don’t be sad if your P’s over point-O-five,
Just try again with samples twice the size,
Everything is possible, just trust in me:
Put your faith in the P.

The F test, the Z test, the chi-square and the T
And other cryptic terminology
Anova, regression, tests distribution-free,
They all need some sort of guarantee.
So if you find a tiny effect size
The P-value will be a good disguise.

There’s no values like P-values,
The frequentist’s hero,
When you get that data modeling feeling
But results you have are not a lot,
You will need some stats that are appealing
To show the journals your work is hot!

There’s no values like P-values
Especially when they’re low
Don’t be sad if your P’s over point-O-five,
Just try again with samples twice the size
Everything is possible, just trust in me:
Put your faith in the P!

6.3.7 Paramétricos Univariados

6.3.7.1 Teste \(z\) para média de uma amostra

Hipótese avaliada Uma amostra de \(n\) sujeitos (ou objetos) vem de uma população de média \(\mu\) igual a um valor especificado \(\mu_0\)?

Suposições

S1. O desvio padrão universal \(\sigma\) é conhecido.
S2. A amostra foi selecionada aleatoriamente da população que representa.
S3. A distribuição dos dados na população que a amostra representa é normal. Pelo Teorema Central do Limite, tal suposição torna-se menos importante à medida que o tamanho da amostra aumenta.

Testes relacionados

• Teste \(t\) para média de uma amostra, Seção 6.3.7.2.
• Teste dos postos sinalizados de Wilcoxon para uma amostra, Seção 6.3.10.1.

Estatística do teste

Sob \(H_0: \mu = \mu_0\), \(H_0: \mu \ge \mu_0\) ou \(H_0: \mu \le \mu_0\), \[\begin{equation} z_{teste}=\frac{\bar{x}-\mu_0}{\sigma/\sqrt{n}} \sim \mathcal{N}(0,1). \tag{6.13} \end{equation}\]

Valor-p Sob \(H_0: \mu = \mu_0\), \[\begin{equation} \text{Valor-p} = 2P(Z \le -|z_{teste}|). \tag{6.14} \end{equation}\]

Sob \(H_0: \mu \ge \mu_0\), \[\begin{equation} \text{Valor-p} = P(Z \le z_{teste}). \tag{6.15} \end{equation}\]

Sob \(H_0: \mu \le \mu_0\), \[\begin{equation} \text{Valor-p} = P(Z \ge z_{teste}). \tag{6.16} \end{equation}\]

Exemplo 6.23 É desejado testar se a média de altura dos alunos da PUCRS pode ser considerada maior do que 167 cm. A hipótese é portanto unilateral superior na forma \(H_0: \mu \le 167\) vs \(H_1: \mu > 167\). Estudos anteriores indicam que a variável \(X\): ‘altura dos alunos da PUCRS’ tem distribuição normal de média desconhecida (motivo da realização do teste de hipóteses para \(\mu\)) e desvio padrão \(\sigma=14\), indicado por \(X \sim \mathcal{N}(\mu,14)\). De uma amostra aleatória com \(n=25\) pessoas obteve-se \(\bar{x}_{25}=172\). Assim, sob \(H_0\) a estatística do teste pode ser calculada da seguinte maneira: \[z_{teste} = \frac{172-167}{14/\sqrt{25}} \approx 1.786 \approx 1.79.\] Se utilizarmos \(\alpha=0.05\) (unilateral superior), \(z_{cr\acute{\imath}tico}=1.64\). Como a estatística de teste extrapola o valor crítico, i.e., \(1.79 > 1.64\), rejeita-se \(H_0\).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(1.79 > 1.64\).

Conclusão Experimental: A amostra sugere que a média de altura dos alunos da PUCRS deve ser maior do que 167 cm.

Exemplo 6.24 No Exemplo 6.23 é possível calcular o valor-p associado à estatística de teste \(z_{teste} \approx 1.79\). Por ser um teste unilateral superior, basta obter a probabilidade de encontrar um valor tão ou mais extremo que \(z_{teste}\) conforme Equação (6.15). Pela tabela de normal padrão (com precisão inferior à do computador) \[\text{Valor-p} = P(Z \ge 1.79) = 1-P(Z<1.79) = 1-0.9633 = 0.0367.\] Utilizando \(\alpha=0.05\) unilateral decide-se novamente pela rejeição de \(H_0\) uma vez que o valor-p é inferior ao nível de significância, i.e., \(0.0367 < 0.05\). A decisão realizada desta maneira deve sempre ser a mesma quando compara-se a estatística do teste com o(s) valor(es) crítico(s).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(0.0367 < 0.05\).

Conclusão Experimental: A amostra sugere que a média de altura dos alunos da PUCRS deve ser maior do que 167 cm.

Exemplo 6.25 Realizando os Exemplos 6.23 e 6.24 no R.

# Definindo os valores indicados no enunciado
mu0 <- 167
n <- 25
x_bar <- 172
sigma <- 14
(zt <- (x_bar-mu0)/(sigma/sqrt(n))) # estatística do teste

## [1] 1.785714

curve(dnorm(x), -3, 3) # gráfico da normal padrão
abline(v = qnorm(.95), col = 'red') # valor crítico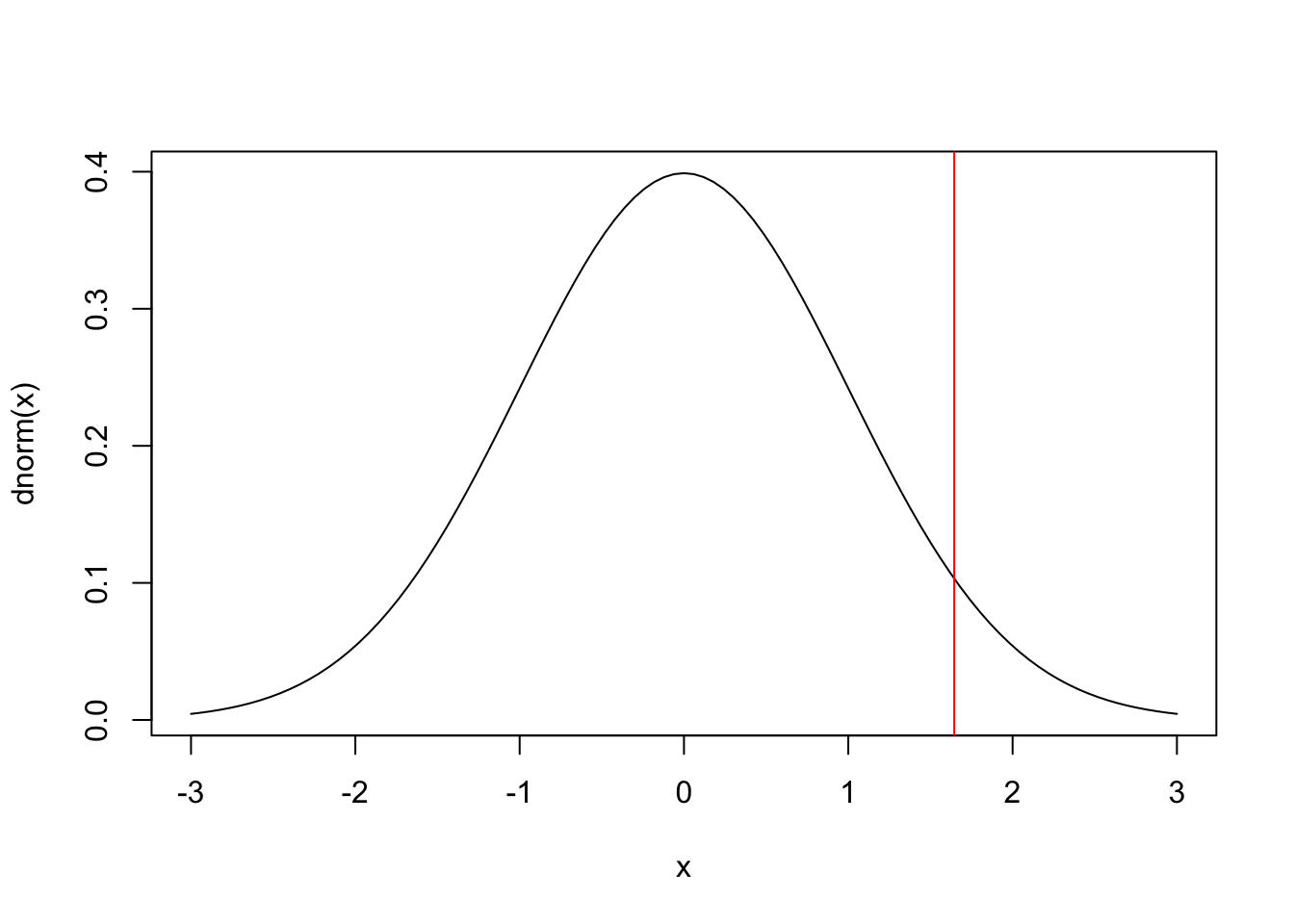

1-pnorm(zt) # p-value mais preciso por conta de zt e pnorm

## [1] 0.03707277

Exemplo 6.26 Em Python.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# Definindo os valores
mu0 = 167
n = 25
x_bar = 172
sigma = 14

# Calculando a estatística do teste
zt = (x_bar - mu0) / (sigma / np.sqrt(n))
print(f"Estatística do teste (zt): {zt:.4f}")  # Output: 1.7857

# Plotando a curva da normal padrão
x = np.linspace(-3, 3, 100)
plt.plot(x, norm.pdf(x))
plt.title('Distribuição Normal Padrão')
plt.xlabel('z')
plt.ylabel('Densidade')

# Adicionando o valor crítico
plt.axvline(x=norm.ppf(0.95), color='red', linestyle='--', 
            label='Valor crítico')
plt.legend()
plt.show()

# Calculando o p-value
p_value = 1 - norm.cdf(zt)
print(f"p-value: {p_value:.4f}")  # Output: 0.0371

6.3.7.2 Teste \(t\) para média de uma amostra

Hipótese avaliada
Uma amostra de \(n\) elementos vem de uma população de média \(\mu\) igual a um valor especificado \(\mu_0\)?

Suposições

S1. A amostra foi selecionada aleatoriamente da população que representa.
S2. A distribuição dos dados na população que a amostra representa é normal.

Testes relacionados

• Teste \(z\) para média de uma amostra, Seção 6.3.7.1.
• Teste dos postos sinalizados de Wilcoxon para uma amostra, Seção 6.3.10.1.

Estatística do teste

Sob \(H_0: \mu = \mu_0\), \[\begin{equation} t_{teste}=\frac{\bar{x}-\mu_0}{s/\sqrt{n}} \sim \mathcal{t}(gl), \tag{6.17} \end{equation}\]

onde \(gl=n-1\) indica os graus de liberdade que definem a distribuição \(t\) conforme Seção 3.9.5.

Valor-p
Sob \(H_0: \mu = \mu_0\), \[\begin{equation} \text{Valor-p} = 2P(T \le -|t_{teste}|). \tag{6.18} \end{equation}\]

Sob \(H_0: \mu \ge \mu_0\), \[\begin{equation} \text{Valor-p} = P(T \le t_{teste}). \tag{6.19} \end{equation}\]

Sob \(H_0: \mu \le \mu_0\), \[\begin{equation} \text{Valor-p} = P(T \ge t_{teste}). \tag{6.20} \end{equation}\]

Exemplo 6.27 É desejado testar se a média de altura dos alunos da PUCRS pode ser considerada maior do que 167 cm. O teste é portanto unilateral superior na forma \(H_0: \mu \le 167\) vs \(H_1: \mu > 167\). Estudos anteriores indicam que a variável \(X\): ‘altura dos alunos da PUCRS’ tem distribuição normal de média e desvio padrão desconhecidos, indicado por \(X \sim \mathcal{N}(\mu,\sigma)\). De uma amostra aleatória com \(n=25\) pessoas obteve-se \(\bar{x}_{25}=172\) e \(s_{25}=14\). Assim, sob \(H_0\) a estatística do teste pode ser calculada da seguinte maneira: \[t_{teste} = \frac{172-167}{14/\sqrt{25}} \approx 1.786.\] Se utilizarmos \(\alpha=0.05\) (unilateral superior), \(t_{cr\acute{\imath}tico}=1.711\), considerando \(gl=24\) graus de liberdade. Como a estatística de teste extrapola o valor crítico, i.e., \(1.786 > 1.711\), rejeita-se \(H_0\).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(1.786 > 1.711\).

Conclusão Experimental: A amostra sugere que a média de altura dos alunos da PUCRS deve ser maior do que 167 cm.

Exemplo 6.28 No Exemplo 6.27 é possível obter um intervalo para o valor-p associado à estatística de teste \(t_{teste} \approx 1.786\). Por ser um teste unilateral superior, deve-se obter a probabilidade de encontrar um valor tão ou mais extremo que \(t_{teste}\) conforme Equação (6.19). Pela tabela de \(t\) com \(gl=24\) graus de liberdade obtém-se \(P(t>1.711) = 0.05\) e \(P(t>2.064) = 0.025\). Dada a limitação de precisão da tabela \(t\), pode-se apenas concluir que \(0.025 < P(t>1.786) < 0.05\). Utilizando \(\alpha=0.05\) unilateral decide-se novamente pela rejeição de \(H_0\) uma vez que o valor-p é inferior ao nível de significância, i.e., \(P(t>1.786) < 0.05\). A decisão realizada desta maneira deve sempre ser a mesma quando compara-se a estatística do teste com o(s) valor(es) crítico(s).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(P(t>1.786) < 0.05\).

Conclusão Experimental: A amostra sugere que a média de altura dos alunos da PUCRS deve ser maior do que 167 cm.

Exemplo 6.29 Realizando os Exemplos 6.27 e 6.28 no R.

# Definindo os valores indicados no enunciado
mu0 <- 167
n <- 25
x_bar <- 172
s <- 14
(tt <- (x_bar-mu0)/(s/sqrt(n))) # estatística do teste, note a maior precisão

## [1] 1.785714

curve(dt(x, df = n-1), -3, 3) # gráfico da t com gl=25-1=24
abline(v = qt(.95, df = n-1), col = 'red') # valor crítico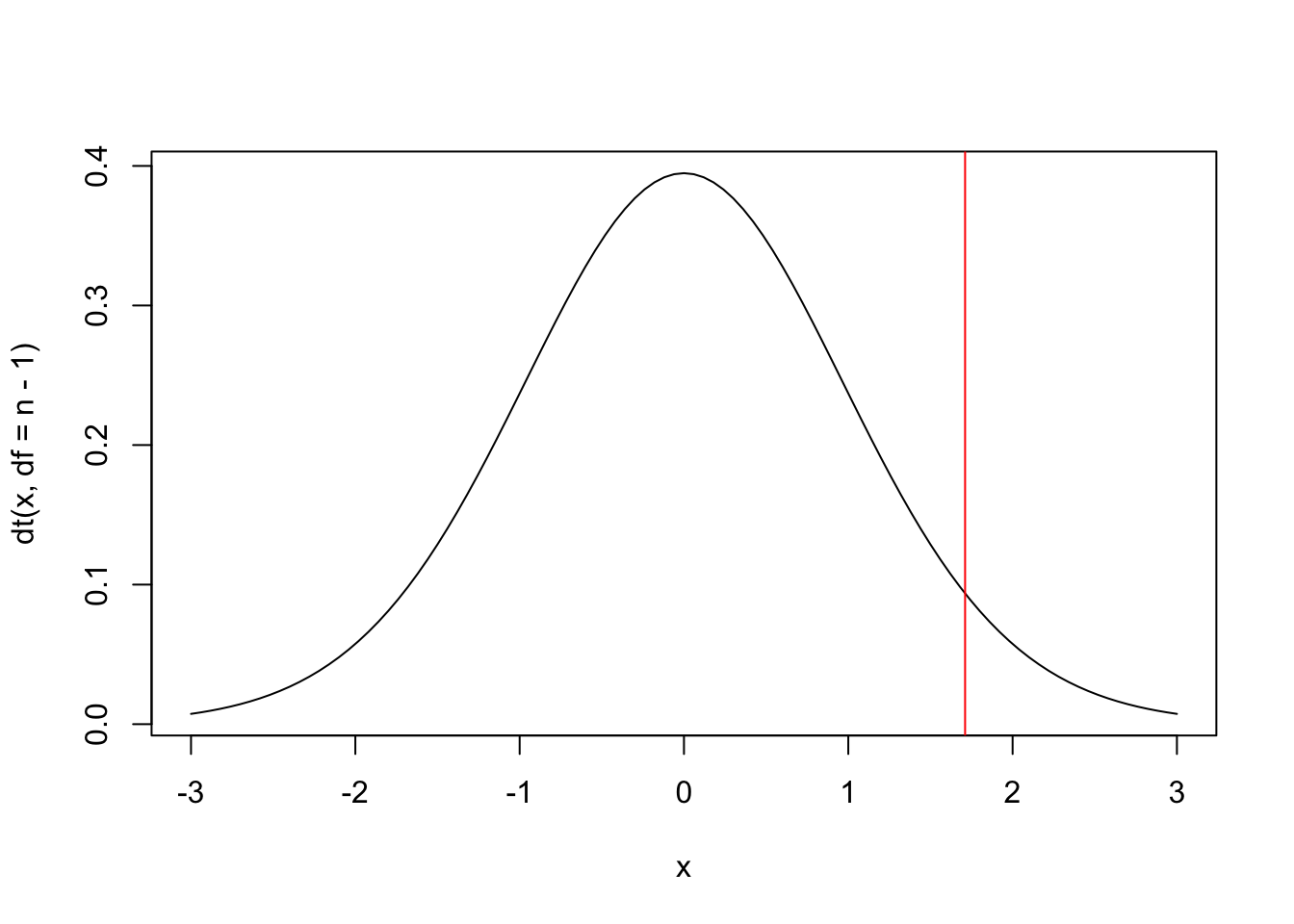

1-pt(tt, df = n-1) # p-value mais preciso por conta de tt e pt

## [1] 0.04339453

Exemplo 6.30 Em Python.

import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt

# Definindo os valores
mu0 = 167
n = 25
x_bar = 172
s = 14

# Calculando a estatística do teste t
tt = (x_bar - mu0) / (s / np.sqrt(n))
print(f"Estatística do teste (tt): {tt:.4f}")  # Output: 1.7857

# Plotando a curva da distribuição t
x = np.linspace(-3, 3, 100)
plt.plot(x, t.pdf(x, df=n-1))
plt.title('Distribuição t de Student (gl = 24)')
plt.xlabel('t')
plt.ylabel('Densidade')

# Adicionando o valor crítico
plt.axvline(x=t.ppf(0.95, df=n-1), color='red', linestyle='--', 
            label='Valor crítico')
plt.legend()
plt.show()

# Calculando o p-value
p_value = 1 - t.cdf(tt, df=n-1)
print(f"p-value: {p_value:.4f}")  # Output: 0.0429

6.3.7.3 Testes para proporção de uma amostra

Hipótese avaliada
Em uma população composta de duas categorias, a proporção \(\pi\) de observações em uma das categorias é igual a um valor específico \(\pi_0\)?

Suposições
S1. Cada observação pode ser classificada em sucesso ou fracasso.
S2. Cada uma das \(n\) observações (condicionalmente) independentes é selecionada aleatoriamente de uma população.
S3. A probabilidade de sucesso \(\pi\) se mantém constante a cada observação.

Normal (assintótico)

Estatística do teste (assintótico)

Sob \(H_0: \pi = \pi_0\), \[\begin{equation} z_{teste}=\frac{p-\pi_0}{\sqrt{\pi_0 (1-\pi_0)/n}} \sim \mathcal{N}(0,1). \tag{6.21} \end{equation}\]

Valor-p (assintótico)
Sob \(H_0: \pi = \pi_0\), \[\begin{equation} \text{Valor-p} = 2P(Z \le -|z_{teste}|). \tag{6.22} \end{equation}\]

Sob \(H_0: \pi \ge \pi_0\), \[\begin{equation} \text{Valor-p} = P(Z \le z_{teste}). \tag{6.23} \end{equation}\]

Sob \(H_0: \pi \le \pi_0\), \[\begin{equation} \text{Valor-p} = P(Z \ge z_{teste}). \tag{6.24} \end{equation}\]

Binomial (exato)

Valor-p (exato)
Seja \(X\) o número de sucessos em \(n\) ensaios de Bernoulli. Sob \(H_0: \pi = \pi_0\) ocorre que \(X \sim \mathcal{B}(n,\pi_0)\), se \(x>\frac{n}{2}\) e \(I = \{ 0,1,\ldots,n-x, x,\ldots,n \}\), \[\begin{equation} \text{Valor-p} = P(n-x \ge X \ge x | \pi = \pi_0) = \sum_{i \in I} \dbinom{n}{i} \pi_{0}^i (1-\pi_0)^{n-i}, \tag{6.25} \end{equation}\]

se \(x<\frac{n}{2}\) e \(I = \{ 0,1,\ldots,x, n-x,\ldots,n \}\), \[\begin{equation} \text{Valor-p} = P(x \ge X \ge n-x | \pi = \pi_0) = \sum_{i \in I} \dbinom{n}{i} \pi_{0}^i (1-\pi_0)^{n-i}, \tag{6.26} \end{equation}\]

e \(\text{Valor-p} = 1\) se \(x=\frac{n}{2}\).

Sob \(H_0: \pi \le \pi_0\), \[\begin{equation} \text{Valor-p} = P(X \ge x | \pi = \pi_0) = \sum_{i=x}^{n} \dbinom{n}{i} \pi_{0}^i (1-\pi_0)^{n-i} \tag{6.27} \end{equation}\]

Sob \(H_0: \pi \ge \pi_0\), \[\begin{equation} \text{Valor-p} = P(X \le x | \pi = \pi_0) = \sum_{i=0}^{x} \dbinom{n}{i} \pi_{0}^i (1-\pi_0)^{n-i} \tag{6.28} \end{equation}\]

Exemplo 6.31 Suponha que deseja-se testar \(\pi\), a proporção de caras em uma moeda, na forma \(H_0: \pi \le 0.5\) vs \(H_1 : \pi > 0.5\). Para isso a moeda é lançada \(n=12\) vezes, onde se observam \(x=9\) caras e \(n-x=12-9=3\) coroas. Sabe-se que \(p=\frac{9}{12}=\frac{3}{4}=0.75\). Considerando a abordagem assintótica, sob \(H_0\) \[z_{teste}=\frac{0.75-0.5}{\sqrt{0.5 (1-0.5)/12}} \approx 1.73.\] Se utilizarmos \(\alpha=0.05\) (unilateral superior), \(z_{cr\acute{\imath}tico}=1.64\). Como a estatística de teste extrapola o valor crítico, i.e., \(1.73 > 1.64\), rejeita-se \(H_0\).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(1.73 > 1.64\).

Conclusão Experimental: A amostra sugere que a proporção de caras da moeda deve ser considerada maior que 0.5.

Exemplo 6.32 Considere novamente os dados do Exemplo 6.31. Pela Equação (6.16) utilizando a tabela de normal padrão (com precisão inferior à do computador), \[\text{Valor-p} = P(Z \ge 1.73) = 1-P(Z<1.73) = 1-0.9582 = 0.0418.\] Utilizando \(\alpha=0.05\) unilateral decide-se novamente pela rejeição de \(H_0\) uma vez que o valor-p é inferior ao nível de significância, i.e., \(0.0418 < 0.05\). A decisão realizada desta maneira deve sempre ser a mesma quando compara-se a estatística do teste com o(s) valor(es) crítico(s).

Decisão Estatística: Rejeita-se \(H_0\) com \(\alpha=5\%\) pois \(0.0418 < 0.05\).

Conclusão Experimental: A amostra sugere que a proporção de caras da moeda deve ser considerada maior que 0.5.

Exemplo 6.33 Realizando os Exemplos 6.31 e 6.32 no R.

n <- 12
x <- 9
(p <- x/n)

## [1] 0.75

pi0 <- 0.5
(zt <- (p-pi0)/sqrt(pi0*(1-pi0)/n))

## [1] 1.732051

1-pnorm(zt) # p-value mais preciso por conta de zt e pnorm

## [1] 0.04163226

# usando a função prop.test, sem a correção de Yates
prop.test(x, n, pi0, alternative = 'greater', correct = FALSE)

## 
##  1-sample proportions test without continuity correction
## 
## data:  x out of n, null probability pi0
## X-squared = 3, df = 1, p-value = 0.04163
## alternative hypothesis: true p is greater than 0.5
## 95 percent confidence interval:
##  0.512662 1.000000
## sample estimates:
##    p 
## 0.75

Exemplo 6.34 Em Python.

import numpy as np
from scipy.stats import norm
from statsmodels.stats.proportion import proportions_ztest

# Parâmetros
n = 12
x = 9
p = x / n
pi0 = 0.5

# Calculando a estatística do teste z
zt = (p - pi0) / np.sqrt(pi0 * (1 - pi0) / n)
print(f"Estatística do teste (zt): {zt:.4f}")  # Output: 2.1909

# Calculando o p-value
p_value = 1 - norm.cdf(zt)
print(f"p-value: {p_value:.4f}")  # Output: 0.0142

# Função proportions_ztest (similar a prop.test sem correção)
z_stat, p_value = proportions_ztest(x, n, value=pi0, alternative='larger')
print(f"\nTeste de proporção: z = {z_stat:.4f}, p = {p_value:.4f}")

Exemplo 6.35 Considere novamente os dados do Exemplo 6.31. O teste exato pode ser realizado considerando que sob \(H_0: \pi \le 0.5\), o número de caras (sucessos) \(X\) tem distribuição binomial de parâmetros \(n=12\) e \(\pi=0.5\), i.e., \(X \sim \mathcal{B}(12,0.5)\). Assim, o valor-p exato resulta em \[\begin{equation} Pr\left( X \geq 9 | \pi = 0.5 \right) = \left[ \binom {12}{9} + \binom {12}{10} + \binom {12}{11} + \binom {12}{12} \right] \times 0.5^{12} \approx 0.0730. \nonumber \end{equation}\] Note a diferença do valor exato em comparação ao assintótico.

Decisão Estatística: não se rejeita \(H_0\) com \(\alpha=5\%\) pois \(0.0730 > 0.05\).

Conclusão Experimental: a amostra sugere que a proporção de caras da moeda pode ser considerada menor ou igual a 0.5.

Exemplo 6.36 Realizando o Exemplo 6.35 no R.

# Manualmente
n <- 12
x <- 9
pi0 <- 0.5
p9 <- dbinom(9,n,pi0)
p10 <- dbinom(10,n,pi0)
p11 <- dbinom(11,n,pi0)
p12 <- dbinom(12,n,pi0)
p9+p10+p11+p12 # valor-p

## [1] 0.07299805

# Usando a função binom.test
binom.test(x, n, pi0, alternative = 'greater')

## 
##  Exact binomial test
## 
## data:  x and n
## number of successes = 9, number of trials = 12, p-value = 0.073
## alternative hypothesis: true probability of success is greater than 0.5
## 95 percent confidence interval:
##  0.4726734 1.0000000
## sample estimates:
## probability of success 
##                   0.75

# Função prop.test (assintótico mas com correção de continuidade de Yates)
prop.test(x, n, pi0, alternative = 'greater')

## 
##  1-sample proportions test with continuity correction
## 
## data:  x out of n, null probability pi0
## X-squared = 2.0833, df = 1, p-value = 0.07446
## alternative hypothesis: true p is greater than 0.5
## 95 percent confidence interval:
##  0.4713103 1.0000000
## sample estimates:
##    p 
## 0.75

Exemplo 6.37 Em Python.

from scipy.stats import binom
from statsmodels.stats.proportion import proportions_ztest

# Parâmetros
n = 12
x = 9
pi0 = 0.5

# Calculando as probabilidades manualmente
p9 = binom.pmf(9, n, pi0)
p10 = binom.pmf(10, n, pi0)
p11 = binom.pmf(11, n, pi0)
p12 = binom.pmf(12, n, pi0)
p_value_manual = p9 + p10 + p11 + p12
print(f"Valor-p: {p_value_manual:.4f}")  # Output: 0.0730

# Usando binom_test (similar a binom.test)
p_value_binom_test = binom.sf(x - 1, n, pi0)
print(f"Valor-p: {p_value_binom_test:.4f}")  # Output: 0.0730

# Usando proportions_ztest (similar a prop.test com correção de Yates)
z_stat, p_value_prop_test = proportions_ztest(x, n, value=pi0, 
                                              alternative='larger')
print(f"Valor-p: {p_value_prop_test:.4f}")  # Output: 0.1032

Exercício 6.10 Refaça os Exemplos 6.31, 6.32 e 6.35 considerando \(H_0: \pi = 0.6\) vs \(H_1 : \pi \ne 0.6\).

Exercício 6.11 Você é responsável por avaliar a qualidade de um grande lote de peças de segunda mão adquiridas pela sua empresa. O fabricante afirma haver no máximo 10% de peças defeituosas, e você decide investigar. Para isso você retira uma amostra de 50 peças, das quais 9 são defeituosas. Qual a sua opinião sobre o lote adquirido, considerando níveis de significância de 1%, 5% e 10%? Defina as hipóteses, apresentando a Decisão Estatística e a Conclusão Experimental.

6.3.7.4 Teste qui-quadrado para a variância populacional de uma amostra

Hipótese avaliada Uma amostra de \(n\) sujeitos (ou objetos) vem de uma população na qual a variância \(\sigma^2\) é igual a um valor especificado \(\sigma_0^2\)?

Suposições

S1. A amostra foi selecionada aleatoriamente da população que representa.
S2. A distribuição dos dados na população que a amostra representa é normal.

Estatística do teste

Sob \(H_0: \sigma^2 = \sigma_0^2\), \[\begin{equation} \chi_{teste}^2=\frac{(n-1)s^2}{\sigma_0^2} \sim \mathcal{\chi}^2(gl), \tag{6.29} \end{equation}\]

onde \(gl=n-1\) indica os graus de liberdade que definem a distribuição \(\chi^2\) conforme Seção 3.9.4.

Valor-p

Sob \(H_0: \sigma^2 = \sigma_0^2\), \[\begin{equation} \text{Valor-p} = 2P(\chi^2 \le \chi_{teste}^2). \tag{6.30} \end{equation}\]

Sob \(H_0: \sigma^2 \ge \sigma_0^2\), \[\begin{equation} \text{Valor-p} = P(\chi^2 \le \chi_{teste}^2). \tag{6.31} \end{equation}\]

Sob \(H_0: \sigma^2 \le \sigma_0^2\), \[\begin{equation} \text{Valor-p} = P(\chi^2 \ge \chi_{teste}^2). \tag{6.32} \end{equation}\]

Exemplo 6.38 Deseja-se testar se a variância de uma variável com distribuição normal pode ser considerada igual a 5, i.e., \(H_0: \sigma^2 = 5\) vs \(H_0: \sigma^2 \ne 5\). Para isso observa-se uma amostra de tamanho \(n=41\), de onde se calcula uma variância amostral de \(s^2 \approx 3.196876\). Sob \(H_0\) \[\chi_{teste}^2=\frac{(41-1) \times 3.196876 }{5} \approx 25.58.\] Considerando \(\alpha=0.05\) (bilateral) e a tabela qui-quadrado com \(gl=41-1=40\), \(\chi_{cr\acute{\imath}tico1}^2=24.43\) e \(\chi_{cr\acute{\imath}tico2}^2=59.34\). Como a estatística de teste não extrapola os valores críticos, i.e., \(24.43 < 25.58 < 59.34\), não se rejeita \(H_0\).

Decisão Estatística: Não se rejeita \(H_0\) com \(\alpha=0.05\) pois \(24.43 < 25.58 < 59.34\).

Conclusão Experimental: A amostra sugere que a variância da referida variável pode ser considerada igual a 5.

Exemplo 6.39 Realizando o Exemplo 6.38 no R.

# Definindo os valores indicados no enunciado
sigma2_0 <- 5
n <- 41
set.seed(123); x <- rnorm(n, mean = 0, sd = 2)
(s2 <- var(x))

## [1] 3.196876

(quit <- ((n-1)*s2)/sigma2_0) # estatística do teste

## [1] 25.57501

curve(dchisq(x, df = n-1), 0, 80) # gráfico da qui^2 com gl=40
(qui_cr1 <- qchisq(.025, df = n-1)) # valor crítico 1

## [1] 24.43304

(qui_cr2 <- qc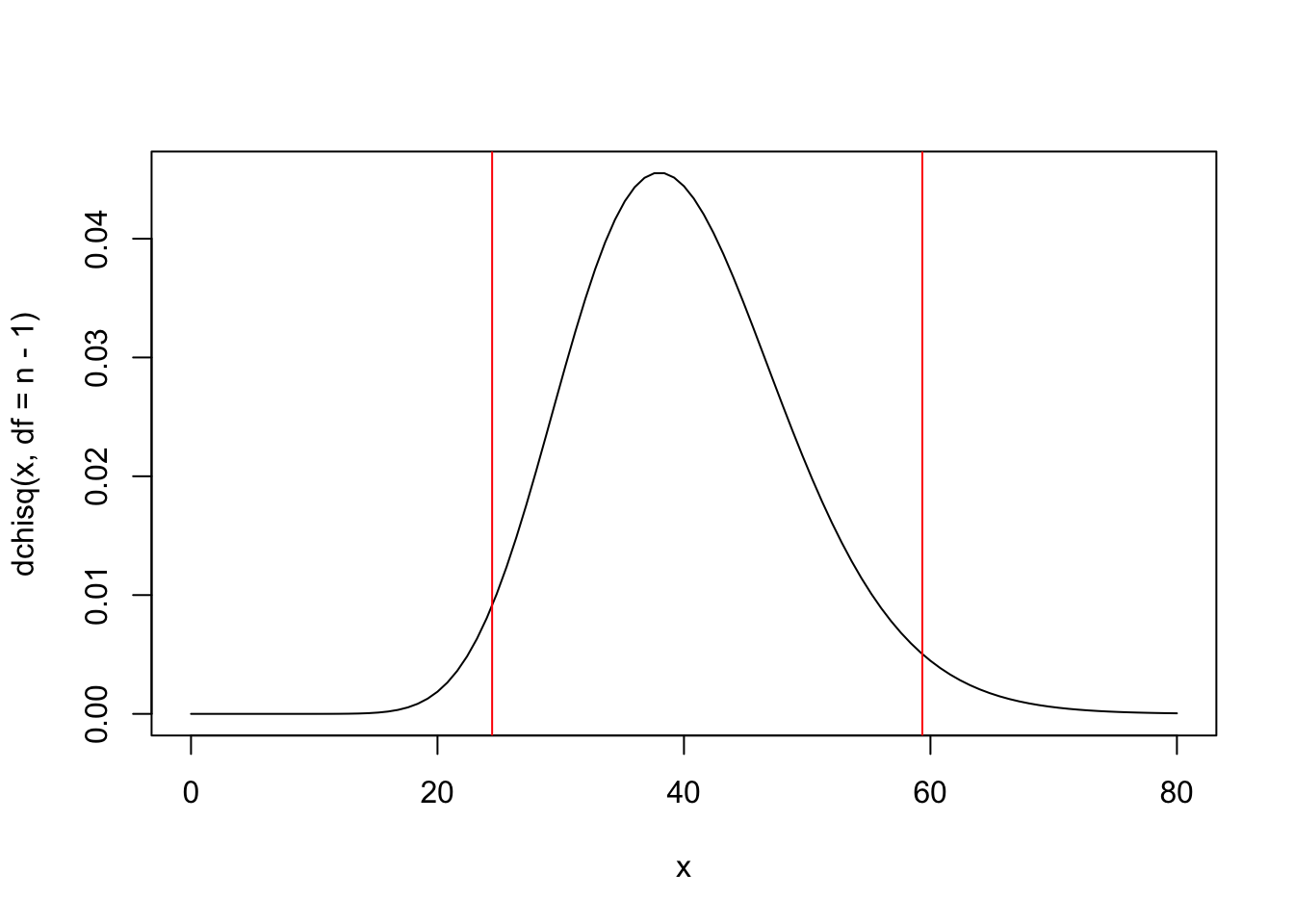hisq(.975, df = n-1)) # valor crítico 2

## [1] 59.34171

abline(v = c(qui_cr1, qui_cr2), col = 'red') # valores críticos

2*pchisq(quit, df = n-1) # p-value bilateral, Eq. (3.24)

## [1] 0.07434994

pchisq(quit, df = n-1) # p-value unilateral inferior, Eq. (3.25)

## [1] 0.03717497

1-pchisq(quit, df = n-1) # p-value unilateral superior, Eq. (3.26)

## [1] 0.962825

# Via pacote DescTools
library(DescTools)
VarTest(x, sigma.squared = sigma2_0, alternative = 'two.sided')

## 
##  One Sample Chi-Square test on variance
## 
## data:  x
## X-squared = 25.575, df = 40, p-value = 0.1069
## alternative hypothesis: true variance is not equal to 5
## 95 percent confidence interval:
##  2.154893 5.233694
## sample estimates:
## variance of x 
##      3.196876

VarTest(x, sigma.squared = sigma2_0, alternative = 'less')

## 
##  One Sample Chi-Square test on variance
## 
## data:  x
## X-squared = 25.575, df = 40, p-value = 0.03717
## alternative hypothesis: true variance is less than 5
## 95 percent confidence interval:
##  0.00000 4.82378
## sample estimates:
## variance of x 
##      3.196876

VarTest(x, sigma.squared = sigma2_0, alternative = 'greater')

## 
##  One Sample Chi-Square test on variance
## 
## data:  x
## X-squared = 25.575, df = 40, p-value = 0.9628
## alternative hypothesis: true variance is greater than 5
## 95 percent confidence interval:
##  2.293374      Inf
## sample estimates:
## variance of x 
##      3.196876

Exemplo 6.40 Em Python.

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt

# Definindo os valores
sigma2_0 = 5
n = 41

# Gerando os dados
np.random.seed(123)
x = np.random.normal(loc=0, scale=2, size=n)

# Calculando a variância amostral
s2 = np.var(x, ddof=1)  # ddof=1 para variância amostral
print(f"Variância amostral: {s2:.4f}")  # Output: 3.6551

# Calculando a estatística do teste qui-quadrado
quit = ((n - 1) * s2) / sigma2_0
print(f"Estatística do teste: {quit:.4f}")  # Output: 29.6063

# Plotando a curva da distribuição qui-quadrado
x_range = np.linspace(0, 80, 500)
plt.plot(x_range, chi2.pdf(x_range, df=n-1))
plt.title(r'Distribuição $\chi^2$ (gl = 40)')
plt.xlabel(r'$\chi^2$')
plt.ylabel('Densidade')

# Adicionando os valores críticos
qui_cr1 = chi2.ppf(0.025, df=n-1)
qui_cr2 = chi2.ppf(0.975, df=n-1)
plt.axvline(x=qui_cr1, color='red', linestyle='--', 
            label='Valor crítico inferior')
plt.axvline(x=qui_cr2, color='red', linestyle='--', 
            label='Valor crítico superior')
plt.legend()
plt.show()

# Calculando os p-values
p_value_bilateral = 2 * chi2.cdf(quit, df=n-1)
p_value_unilateral_inferior = chi2.cdf(quit, df=n-1)
p_value_unilateral_superior = 1 - chi2.cdf(quit, df=n-1)

print(f"p-value bilateral: {p_value_bilateral:.4f}")  # Output: 0.9302
print(f"p-value un. inf.: {p_value_unilateral_inferior:.4f}")  # Output: 0.4651
print(f"p-value un. sup.: {p_value_unilateral_superior:.4f}")  # Output: 0.5349

Exercício 6.12 Suponha que o comprimento de peças em uma fábrica, simbolizado por \(X\), tenha distribuição normal de média e variância desconhecidas, anotado por \(X \sim \mathcal{N}(\mu,\sigma)\). A especificação indica média de 140cm, e desvio padrão de 7cm. Se em uma amostra de 64 peças foi observada uma média de \(\bar{x}=138\)cm e um desvio padrão de \(s=12\)cm, realize os testes de hipóteses apropriados para avaliar se as especificações estão sendo cumpridas.

6.3.7.5 Teste qui-quadrado de aderência de uma amostra

Hipótese avaliada

No universo representado por uma amostra, há diferença entre as frequências esperadas e observadas?

Suposições

S1. Os dados avaliados consistem em uma amostra aleatória de \(n\) observações (condicionalmente) independentes.
S2. Os dados representam frequências de \(k\) categorias mutuamente exclusivas.

Estatística do teste

Sob \(H_0: \pi_1=\pi_1^0, \pi_2=\pi_2^0, \ldots, \pi_k=\pi_k^0\), \[\begin{equation} \chi_{teste}^2 = \sum_{i=1}^{k} \frac{(O_{i}-E_{i})^2}{E_{i}} \sim \chi^2(gl), \tag{6.33} \end{equation}\]

onde \(E_{i}=n\pi_i^0\), \(k\) é o número de categorias e \(gl=k-1\) indica os graus de liberdade que definem a distribuição \(\chi^2\) conforme Seção 3.9.4.

Valor-p

Sob \(H_0: \pi_1=\pi_1^0, \pi_2=\pi_2^0, \ldots, \pi_k=\pi_k^0\), \[\begin{equation} \text{Valor-p} = P(\chi^2 \ge \chi_{teste}^2). \tag{6.34} \end{equation}\]

Exemplo 6.41 (Adaptado de (Sheskin 2011, 278) - Teste qui-quadrado de aderência balanceado) Um dado é lançado 120 vezes, a fim de determinar se pode ou não ser considerado equilibrado. Os valores observados estão apresentados conforme tabela abaixo, e \(E_i=120 \times \frac{1}{6}=20, i \in \{1,2,3,4,5,6\}\).

Face (\(i\))	1	2	3	4	5	6
\(O_{i}\)	20	14	18	17	22	29
\(E_{i}\)	20	20	20	20	20	20

Sob \(H_0: \pi_1=\frac{1}{6}, \pi_2=\frac{1}{6}, \pi_3=\frac{1}{6}, \pi_4=\frac{1}{6}, \pi_5=\frac{1}{6}, \pi_6=\frac{1}{6}\), \[\chi_{teste}^2 = \frac{(20-20)^2}{20} + \frac{(14-20)^2}{20} + \frac{(18-20)^2}{20} + \frac{(17-20)^2}{20} + \frac{(22-20)^2}{20} + \frac{(29-20)^2}{20} = 6.7.\] Considerando \(\alpha=0.05\) (unilateral superior, que é sempre o caso deste teste) e a tabela qui-quadrado com \(gl=6-1=5\), \(\chi_{cr\acute{\imath}tico}^2=11.07\). Como a estatística de teste não extrapola os valores críticos, i.e., \(6.7 < 11.07\), não se rejeita \(H_0\). Considerando a Equação (6.34) e a função stats::pchisq(), \[\text{Valor-p} = P(\chi^2 \ge 6.7) \approx 0.2439.\]

Decisão Estatística: Não se rejeita \(H_0\) com \(\alpha=0.05\) pois \(6.7 < 11.07\) ou \(0.2439 > 0.05\).

Conclusão Experimental: A amostra sugere que o dado deve ser equilibrado.

curve(dchisq(x, df=5), 0, 20) # gráfico da qui^2 com gl=6-1=5
(qui_cr <- qchisq(.95, df=5)) # valor crítico

## [1] 11.0705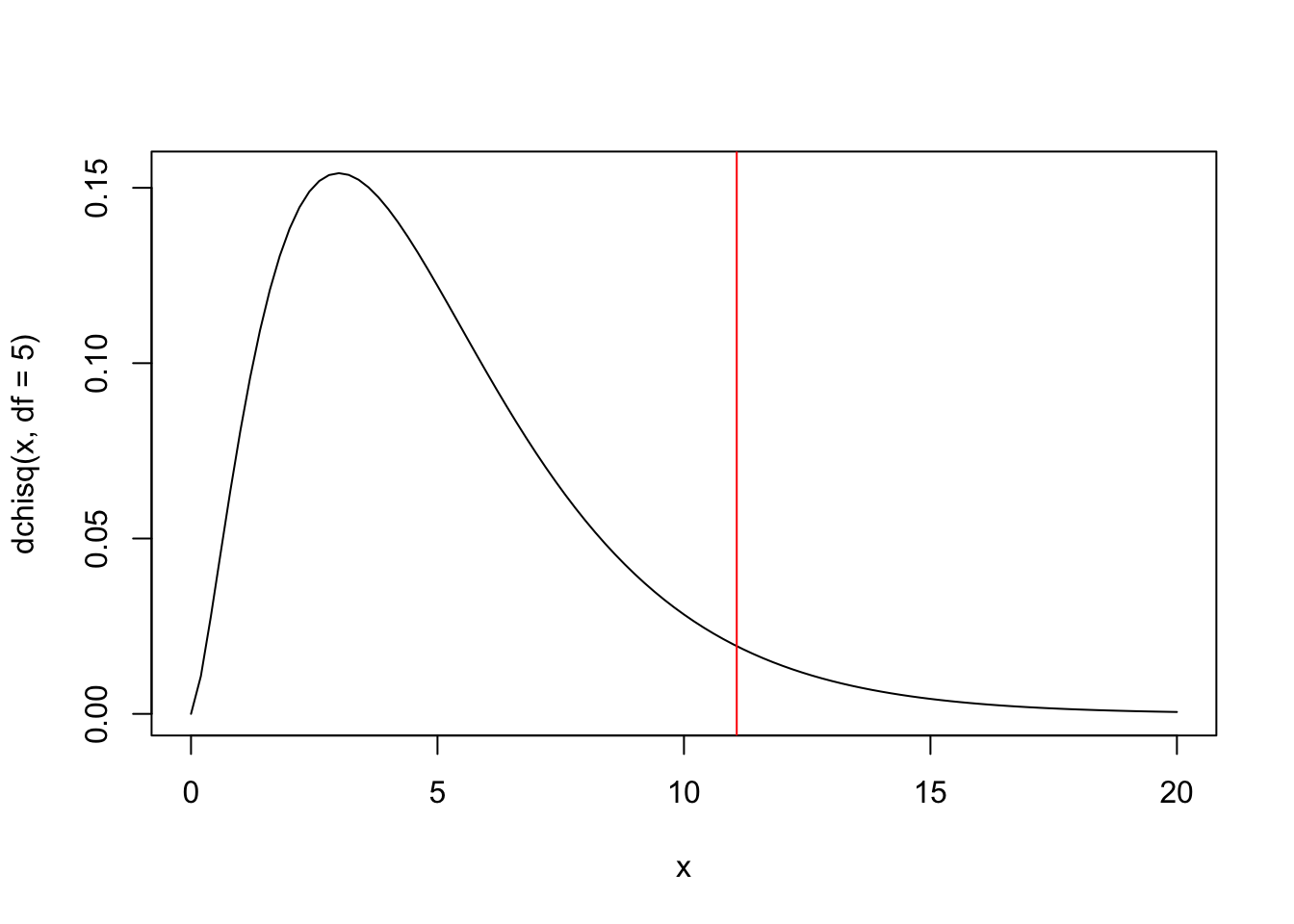

abline(v = qui_cr, col='red') # valor crítico no gráfico

o <- c(20,14,18,17,22,29)     # Observados
n <- sum(o)          # Tamanho da amostra
p <- rep(1/6,6)      # Distribuição uniforme (dado equilibriado)
e <- n*p             # Valores esperados se o dado for equilibrado
k <- length(o)       # Número de categorias
(qui <- sum((o-e)^2/e)) # Equação (3.25)

## [1] 6.7

1-pchisq(qui,k-1)       # p-value

## [1] 0.2439246

chisq.test(o)           # Pela função 'chisq.test'

## 
##  Chi-squared test for given probabilities
## 
## data:  o
## X-squared = 6.7, df = 5, p-value = 0.2439

Exemplo 6.42 Em Python.

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt

# Plotando a curva da distribuição qui-quadrado
x_range = np.linspace(0, 20, 500)
plt.plot(x_range, chi2.pdf(x_range, df=5))
plt.title(r'Distribuição $\chi^2$ (gl = 5)')
plt.xlabel(r'$\chi^2$')
plt.ylabel('Densidade')

# Adicionando o valor crítico
qui_cr = chi2.ppf(0.95, df=5)
plt.axvline(x=qui_cr, color='red', linestyle='--', 
            label='Valor crítico')
plt.legend()
plt.show()

# Dados observados
o = np.array([20, 14, 18, 17, 22, 29])

# Calculando a estatística qui-quadrado
n = np.sum(o)  # Tamanho da amostra
p = np.repeat(1/6, 6)  # Probabilidades esperadas
e = n * p  # Valores esperados
k = len(o)  # Número de categorias
qui = np.sum((o - e)**2 / e)
print(f"Estatística qui-quadrado: {qui:.4f}") # Output: 5.2000

# Calculando o p-value
p_value = 1 - chi2.cdf(qui, df=k-1)
print(f"p-value: {p_value:.4f}") # Output: 0.3921

# Usando a função chisquare (similar a chisq.test)
from scipy.stats import chisquare
chi2_stat, p_value = chisquare(o, f_exp=e)
print(f"\nTeste qui-quadrado: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}")

Exemplo 6.43 (Teste qui-quadrado de aderência desbalanceado) Gregor Mendel conduziu experimentos sobre hereditariedade em ervilhas. Em suma, as ervilhas podiam ser redondas (R) ou enrugadas (E), amarelas (A) ou verdes (V). Portanto, existem quatro combinações possíveis: RA, RV, EA, EV. Se sua teoria estivesse correta, as ervilhas seriam observadas na proporção de 9:3:3:1. Se o resultado do experimento produziu os seguintes dados observados, pode-se avaliar se há indícios da proporção considerada⁴⁴.

\(i\)	RA (1)	RV (2)	EA (3)	EV (4)	\(n\)
\(O_i\)	315	108	101	32	556
\(E_i\)	312.75	104.25	104.25	34.75	556

Sob \(H_0: \pi_1=\frac{9}{16}, \pi_2=\frac{3}{16}, \pi_3=\frac{3}{16}, \pi_4=\frac{1}{16}\), \[\chi_{teste}^2 = \frac{(315-312.75)^2}{312.75} + \frac{(108-104.25)^2}{104.25} + \frac{(101-104.25)^2}{104.25} + \frac{(32-34.75)^2}{34.75} \approx 0.47.\] Considerando \(\alpha=0.05\) (unilateral superior, que é sempre o caso deste teste) e a tabela qui-quadrado com \(gl=4-1=3\), \(\chi_{cr\acute{\imath}tico}^2=7.81\). Como a estatística de teste não extrapola os valores críticos, i.e., \(0.47 < 7.81\), não se rejeita \(H_0\). Considerando a Equação (6.34) e a função pchisq, \[\text{Valor-p} = P(\chi^2 \ge 0.47) \approx 0.9254.\]

Decisão Estatística: Não se rejeita \(H_0\) com \(\alpha=0.05\) pois \(0.47 < 7.81\) ou \(0.9254 > 0.05\).

Conclusão Experimental: A amostra sugere que a proporção das ervilhas deve ser 9:3:3:1.

o <- c(315,108,101,32)      # Observados
(n <- sum(o))               # Tamanho da amostra

## [1] 556

(k <- length(o))            # Número de categorias

## [1] 4

p <- c(9/16,3/16,3/16,1/16) # Proporção 9:3:3:1
(e <- n*p)              # Valores esperados se a prop. for 9:3:3:1

## [1] 312.75 104.25 104.25  34.75

(qui <- sum((o-e)^2/e))     # Estatística do teste

## [1] 0.470024

1-pchisq(qui,k-1)           # Valor-p

## [1] 0.9254259

chisq.test(o,p=p)           # Pela função 'chisq.test'

## 
##  Chi-squared test for given probabilities
## 
## data:  o
## X-squared = 0.47002, df = 3, p-value = 0.9254

Exemplo 6.44 Em Python.

import numpy as np
from scipy.stats import chisquare

# Dados observados
o = np.array([315, 108, 101, 32])

# Calculando a estatística qui-quadrado
n = np.sum(o)  # Tamanho da amostra
k = len(o)  # Número de categorias
p = np.array([9/16, 3/16, 3/16, 1/16]) # Probabilidades esperadas
e = n * p  # Valores esperados
qui = np.sum((o - e)**2 / e)
print(f"Estatística qui-quadrado: {qui:.4f}") # Output: 0.4706

# Calculando o p-value
p_value = 1 - chi2.cdf(qui, df=k-1)
print(f"p-value: {p_value:.4f}")  # Output: 0.9254

# Usando a função chisquare (similar a chisq.test)
chi2_stat, p_value = chisquare(o, f_exp=e)
print(f"\nTeste qui-quadrado: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}")

6.3.8 Paramétricos Bivariados

6.3.8.1 Teste F (de Hartley) de homogeneidade de variâncias

O teste F (de Hartley) de igualdade de variâncias foi proposto por (H. O. Hartley 1950). Implementado em stats::var.test() é um caso especial do teste de Bartlett (Bartlett 1937).

Hipótese avaliada

A variância do universo 1 é igual à variância do universo 2.

Suposições

S1. Os tamanhos de amostra \(n_1\) e \(n_2\) são similares.

Testes relacionados

• Testes de homogeneidade de variâncias, Seção 6.3.12.1.

Estatística do teste

Sob \(H_0: \sigma_1=\sigma_2\), \[\begin{equation} F_{max}=\frac{s_{max}^2}{s_{min}^2} \sim \mathcal{F}(n_{max}-1,n_{min}-1), \tag{6.35} \end{equation}\]

onde \(s_{max}^2\) e \(s_{min}^2\) são respectivamente a maior e menor variância amostral, e \(n_{max}\) e \(n_{min}\) correspondem respectivamente ao tamanho de amostra associado à amostra de maior e menor variância.

Valor-p

Sob \(H_0: \sigma_1=\sigma_2\), \[\begin{equation} \text{Valor-p} = 2P(F \ge F_{max}). \tag{6.36} \end{equation}\]

Sob \(H_0: \sigma_1 \ge \sigma_2\), \[\begin{equation} \text{Valor-p} = P(F \ge F_{max}). \tag{6.37} \end{equation}\]

Sob \(H_0: \sigma_1 \le \sigma_2\), \[\begin{equation} \text{Valor-p} = P(F < F_{max}). \tag{6.38} \end{equation}\]

x <- 1:10
y <- c(7:20)
nx <- length(x)
ny <- length(y)
(Fmax <- var(y)/var(x))

## [1] 1.909091

2*(1-pf(Fmax,ny-1,nx-1)) # bilateral

## [1] 0.3342733

1-pf(Fmax,ny-1,nx-1) # unilateral inferior

## [1] 0.1671366

pf(Fmax,ny-1,nx-1) # unilateral superior

## [1] 0.8328634

# Utilizando a função var.test
var.test(x,y) # H_0: bilateral

## 
##  F test to compare two variances
## 
## data:  x and y
## F = 0.52381, num df = 9, denom df = 13, p-value = 0.3343
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.1581535 2.0065024
## sample estimates:
## ratio of variances 
##          0.5238095

var.test(x,y, alternative = 'less') # unilateral inferior

## 
##  F test to compare two variances
## 
## data:  x and y
## F = 0.52381, num df = 9, denom df = 13, p-value = 0.1671
## alternative hypothesis: true ratio of variances is less than 1
## 95 percent confidence interval:
##  0.000000 1.596335
## sample estimates:
## ratio of variances 
##          0.5238095

var.test(x,y, alternative = 'greater') # unilateral superior

## 
##  F test to compare two variances
## 
## data:  x and y
## F = 0.52381, num df = 9, denom df = 13, p-value = 0.8329
## alternative hypothesis: true ratio of variances is greater than 1
## 95 percent confidence interval:
##  0.1929775       Inf
## sample estimates:
## ratio of variances 
##          0.5238095

Exemplo 6.45 Em Python.

import numpy as np
from scipy.stats import f
from scipy.stats import bartlett

# Dados
x = np.arange(1, 11)
y = np.arange(7, 21)
nx = len(x)
ny = len(y)

# Calculando a estatística F
Fmax = np.var(y, ddof=1) / np.var(x, ddof=1)
print(f"Estatística F (Fmax): {Fmax:.4f}")  # Output: 12.2500

# Calculando os p-values
p_value_bilateral = 2 * (1 - f.cdf(Fmax, dfn=ny-1, dfd=nx-1))
p_value_unilateral_menor = 1 - f.cdf(Fmax, dfn=ny-1, dfd=nx-1)
p_value_unilateral_maior = f.cdf(Fmax, dfn=ny-1, dfd=nx-1)

print(f"p-value bilateral: {p_value_bilateral:.4f}") # Output: 0.0000
print(f"p-value un. inf.: {p_value_unilateral_menor:.4f}") # Output: 0.0000
print(f"p-value un. sup.: {p_value_unilateral_maior:.4f}") # Output: 1.0000

# Usando a função bartlett (similar a var.test)
statistic, p_value = bartlett(x, y)

print(f"\nTeste de Bartlett: statistic = {statistic:.4f}, p = {p_value:.4f}")

6.3.8.2 Teste \(t\) para médias de duas amostras independentes

Hipótese avaliada

Duas amostras independentes representam duas populações com valores médios diferentes?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. A distribuição dos dados na população subjacente de cada amostra é normal.

Testes relacionados

• Teste dos postos de Mann-Whitney para amostras independentes, Seção 6.3.11.2.

Estatística do teste

Sob \(H_0: \mu_1-\mu_2 = \Delta_0\) e \(\sigma_1 = \sigma_2\), \[\begin{equation} t_{teste} = \frac{(\bar{x}_1-\bar{x}_2) - \Delta_0}{\sqrt{\left[ \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2} \right] \left[ \frac{1}{n_1}+\frac{1}{n_2} \right]}} \sim \mathcal{t}(gl). \tag{6.39} \end{equation}\]

Sob \(H_0: \mu_1-\mu_2 = \Delta_0\) e \(\sigma_1 \ne \sigma_2\), \[\begin{equation} t_{teste} = \frac{(\bar{x}_1-\bar{x}_2) - \Delta_0}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \sim \mathcal{t}(gl), \tag{6.40} \end{equation}\]

onde \(n_1\) e \(n_2\) são os tamanhos das amostras, \(\bar{x}_1\) e \(\bar{x}_2\) representam as médias amostrais e \(s_1^2\) e \(s_2^2\) são as variâncias amostrais dos universos 1 e 2. Se as variâncias forem admitidas iguais (\(\sigma_1 = \sigma_2\)), os graus de liberdade são calculados utilizando a expressão \[\begin{equation} gl = n_1 + n_2-2. \tag{6.41} \end{equation}\] No caso de as variâncias serem admitidas diferentes (\(\sigma_1 \ne \sigma_2\)), calculam-se os graus de liberdade com a abordagem de (Welch 1938), dados por \[\begin{equation} gl = \frac{\left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2}{ \frac{(s_1^2/n_1)^2}{n_1-1} + \frac{(s_2^2/n_2)^2}{n_2-1}}. \tag{6.42} \end{equation}\]

Valor-p

Sob \(H_0: \mu_1-\mu_2 = \Delta_0\), \[\begin{equation} \text{Valor-p} = 2P(t \le -|t_{teste}|). \tag{6.43} \end{equation}\]

Sob \(H_0: \mu_1-\mu_2 \ge \Delta_0\), \[\begin{equation} \text{Valor-p} = P(t \le t_{teste}). \tag{6.44} \end{equation}\]

Sob \(H_0: \mu_1-\mu_2 \le \Delta_0\), \[\begin{equation} \text{Valor-p} = P(t \ge t_{teste}). \tag{6.45} \end{equation}\]

Exemplo 6.46 Adaptado da documentação de stats:t.test().

t.test(1:10, y = c(7:20), var.equal = TRUE)  # Eq. 6.39 e 6.41

## 
##  Two Sample t-test
## 
## data:  1:10 and c(7:20)
## t = -5.1473, df = 22, p-value = 3.691e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -11.223245  -4.776755
## sample estimates:
## mean of x mean of y 
##       5.5      13.5

t.test(1:10, y = c(7:20)) # Eq. 6.40 e 6.42 (padrão)

## 
##  Welch Two Sample t-test
## 
## data:  1:10 and c(7:20)
## t = -5.4349, df = 21.982, p-value = 1.855e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -11.052802  -4.947198
## sample estimates:
## mean of x mean of y 
##       5.5      13.5

Exercício 6.13 Obtenha os valores do Exemplo 6.46 a partir das equações.

6.3.8.3 Teste \(t\) para médias de duas amostras dependentes/pareadas

Hipótese avaliada

Duas amostras dependentes representam duas populações com médias diferentes?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. A distribuição dos dados na população subjacente de cada amostra é normal.
S3. (Homogeneidade de variâncias) A variância da população representada pela amostra 1 é igual à variância da população representada pela amostra 2 (\(\sigma_1^2=\sigma_2^2\)).

Testes relacionados

Teste dos postos de Wilcoxon para amostras dependentes/pareadas, Seção 6.3.11.3.

Estatística do teste

Sob \(H_0: \mu_1-\mu_2 = \Delta_0\), \[\begin{equation} t_{teste} = \frac{\bar{D}-\Delta_0}{s_{\bar{D}}/\sqrt{n}} \sim \mathcal{t}(gl), \tag{6.46} \end{equation}\]

onde \[\bar{D} = \frac{\sum D}{n},\] \(D=x_1-x_2\) e \[\begin{equation} s_{\bar{D}} = \sqrt{\left( \frac{\sum D^2}{n} - \bar{D}^2 \right) \left( \frac{n}{n-1} \right)}. \tag{6.47} \end{equation}\]

Valor-p

Sob \(H_0: \mu_1-\mu_2 = \Delta_0\), \[\begin{equation} \text{Valor-p} = 2P(t \le -|t_{teste}|). \tag{6.48} \end{equation}\]

Sob \(H_0: \mu_1-\mu_2 \ge \Delta_0\), \[\begin{equation} \text{Valor-p} = P(t \le t_{teste}). \tag{6.49} \end{equation}\]

Sob \(H_0: \mu_1-\mu_2 \le \Delta_0\), \[\begin{equation} \text{Valor-p} = P(t \ge t_{teste}). \tag{6.50} \end{equation}\]

Exemplo 6.47 Adaptado de (Sheskin 2011, 764), onde um psicólogo conduz um estudo para determinar se as pessoas demonstram mais emotividade quando são expostas a palavras sexualmente explícitas do que quando são expostas a palavras neutras.

# dados
x1 <- c(9,2,1,4,6,4,7,8,5,1)
x2 <- c(8,2,3,2,3,0,4,5,4,0)
# médias ampostrais
mean(x1) # 4.7

## [1] 4.7

mean(x2) # 3.1

## [1] 3.1

# validando suposições
shapiro.test(x1)  # S2, normalidade

## 
##  Shapiro-Wilk normality test
## 
## data:  x1
## W = 0.94398, p-value = 0.5981

shapiro.test(x2)  # S2, normalidade

## 
##  Shapiro-Wilk normality test
## 
## data:  x2
## W = 0.93776, p-value = 0.5284

g <- as.factor(rep(1:2, each = length(x1))) # grupos 1 e 2
car::leveneTest(c(x1,x2), g) # S3 via Levene

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  1   0.777 0.3897
##       18

stats::fligner.test(c(x1,x2), g) # S3 via Fligner-Killeen

## 
##  Fligner-Killeen test of homogeneity of variances
## 
## data:  c(x1, x2) and g
## Fligner-Killeen:med chi-squared = 0.60663, df = 1, p-value = 0.4361

# realizando o teste
D <- x1-x2
n <- length(D)
(mD <- mean(D))

## [1] 1.6

(sD <- sd(D))

## [1] 1.776388

(tt <- mD/(sD/sqrt(n)))

## [1] 2.848276

gl <- n-1
2*(1-pt(tt, gl))

## [1] 0.01914294

# via t.test (facilita uma barbaridade!)
t.test(x1, x2, paired = TRUE)

## 
##  Paired t-test
## 
## data:  x1 and x2
## t = 2.8483, df = 9, p-value = 0.01914
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  0.3292483 2.8707517
## sample estimates:
## mean difference 
##             1.6

Exemplo 6.48 Em Python.

import numpy as np
import pandas as pd
from scipy.stats import shapiro, levene, ttest_rel, fligner

# Dados
x1 = np.array([9, 2, 1, 4, 6, 4, 7, 8, 5, 1])
x2 = np.array([8, 2, 3, 2, 3, 0, 4, 5, 4, 0])

# Médias amostrais
media_x1 = np.mean(x1)
media_x2 = np.mean(x2)

print("Média amostral de x1:", media_x1)
print("Média amostral de x2:", media_x2)

# Validação de Suposições

# Normalidade
shapiro_x1 = shapiro(x1)
shapiro_x2 = shapiro(x2)

print("\nTeste de Shapiro-Wilk para x1:", shapiro_x1)
print("Teste de Shapiro-Wilk para x2:", shapiro_x2)

# Homogeneidade de Variâncias
levene_test = levene(x1, x2)
fligner_test = fligner(x1, x2)

print("\nTeste de Levene:", levene_test)
print("Teste de Fligner:", fligner_test)

# Teste t para Amostras Pareadas
diferencas = x1 - x2
n = len(diferencas)
mD = np.mean(diferencas)
sD = np.std(diferencas, ddof=1)
tt = mD / (sD / np.sqrt(n))
gl = n - 1
p_valor = 2 * (1 - t.cdf(tt, gl))

print("\nResultados do Teste t (cálculo manual):")
print("Média das diferenças (mD):", mD)
print("Desvio padrão das diferenças (sD):", sD)
print("Estatística t:", tt)
print("Graus de liberdade:", gl)
print("Valor-p (bilateral):", p_valor)

# Teste t para Amostras Pareadas (função ttest_rel)
ttest_result = ttest_rel(x1, x2)

print("\nResultados do Teste t (função ttest_rel):", ttest_result)

#Interpretacao
alpha = 0.05  #Nível de significância

print("\nInterpretação:")

#Teste de Shapiro-Wilk
if shapiro_x1[1] > alpha:
  print("Shapiro-Wilk (x1): Não há evidências para rejeitar a normalidade.")
else:
  print("Shapiro-Wilk (x1): Dados não normalmente distribuídos.")

if shapiro_x2[1] > alpha:
  print("Shapiro-Wilk (x2): Não há evidências para rejeitar a normalidade.")
else:
  print("Shapiro-Wilk (x2): Dados não normalmente distribuídos.")

# Teste de Levene e Fligner
if levene_test[1] > alpha:
    print("Levene: Variâncias homogêneas.")
else:
    print("Levene: Variâncias não homogêneas.")

if fligner_test[1] > alpha:
    print("Fligner: Variâncias homogêneas.")
else:
    print("Fligner: Variâncias não homogêneas.")

#Teste t
if ttest_result[1] > alpha:
  print("Teste t: Não há diferença significativa entre as médias.")
else:
  print("Teste t: Há diferença significativa entre as médias.")

Exercício 6.14 Faça o Exemplo 6.47 considerando \(H_0: \mu_1-\mu_2 \ge 0\) e \(H_0: \mu_1-\mu_2 \ge 0\).

6.3.8.4 Testes qui-quadrado para tabelas \(l \times c\)

Hipótese avaliada (geral)

Na(s) população(ões) representada(s) pela(s) amostra(s) em uma tabela de contingência, as frequências de células observadas são diferentes das frequências esperadas?

Hipóteses avaliadas (homogeneidade)

As \(l\) amostras são ou não homogêneas com relação à proporção de observações em cada uma das \(c\) categorias? (ou)

Se os dados forem homogêneos, a proporção de observações na \(j\)-ésima categoria será igual em todas as \(l\) populações?

Hipótese avaliada (independência)

As duas dimensões/variáveis são independentes uma da outra?

Suposições

S1. Os dados avaliados representam uma amostra aleatória composta por \(n\) observações independentes.
S2. Os dados de frequência são categóricos para \(l \times c\) categorias mutuamente exclusivas.
S3. A frequência esperada de cada célula da tabela de contingência é de pelo menos 5.
S4. (Homogeneidade) As somas das linhas e colunas (somas marginais) são predeterminadas/fixas.
S4. (Independência) As somas das linhas e colunas (somas marginais) não são predeterminadas/fixas.

Testes relacionados

No caso de \(l>2\) ou \(c>2\) pode-se considerar uma análise post hoc⁴⁵ para o teste qui-quadrado de Pearson para dados de contagem, proposta por (Beasley and Schumacker 1995), disponível no pacote chisq.posthoc.test (Ebbert 2019).

Estatística do teste (sem correção de Yates)

Sob \(H_0: O_{ij}=E_{ij}\) para todas as células ou \(H_0: \pi_{ij}=(\pi_{i\cdot})(\pi_{\cdot j})\) para todas as \(l \times c\) células, \[\begin{equation} \chi_{teste}^2 = \sum_{i=1}^{l} \sum_{j=1}^{c} \frac{(O_{ij}-E_{ij})^2}{E_{ij}} \sim \chi^2(gl), \tag{6.51} \end{equation}\] onde \[\begin{equation} E_{ij}=\frac{(O_{i \cdot})(O_{\cdot j})}{n}. \tag{6.52} \end{equation}\] \(k\) é o número de categorias e \(gl=(l-1)(c-1)\) indica os graus de liberdade que definem a distribuição \(\chi^2\) conforme Seção 3.9.4.

Estatística do teste (com correção de Yates)

Sob \(H_0: O_{ij}=E_{ij}\) para todas as células ou \(H_0: \pi_{ij}=(\pi_{i\cdot})(\pi_{\cdot j})\) para todas as \(l \times c\) células, \[\begin{equation} \chi_{teste}^2 = \sum_{i=1}^{l} \sum_{j=1}^{c} \frac{(|O_{ij}-E_{ij}|-0.5)^2}{E_{ij}} \sim \chi^2(gl), \tag{6.53} \end{equation}\]

Estatística do teste simplificada para tabelas \(2 \times 2\) (sem correção de Yates)

Sob \(H_0: O_{ij}=E_{ij}\) para todas as células ou \(H_0: \pi_{ij}=(\pi_{i\cdot})(\pi_{\cdot j})\) para todas as \(l \times c\) células, \[\begin{equation} \chi_{teste}^2 = \frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}, \tag{6.54} \end{equation}\] onde \(a\), \(b\), \(c\) e \(d\) são as quantidades conforme tabela a seguir.

	Coluna 1	Coluna 2	Total
Linha 1	\(a\)	\(b\)	a+b
Linha 2	\(c\)	\(d\)	c+d
Total	\(a+c\)	\(b+d\)	n

Estatística do teste simplificada para tabelas \(2 \times 2\) (com correção de Yates)

Sob \(H_0: O_{ij}=E_{ij}\) para todas as células ou \(H_0: \pi_{ij}=(\pi_{i\cdot})(\pi_{\cdot j})\) para todas as \(l \times c\) células, \[\begin{equation} \chi_{teste}^2 = \frac{n(|ad-bc|-0.5n)^2}{(a+b)(c+d)(a+c)(b+d)}. \tag{6.55} \end{equation}\]

Exemplo 6.49 (Adaptado de (Sheskin 2011, 639), teste de homogeneidade) Um pesquisador realiza um estudo para avaliar o efeito do ruído no comportamento altruísta. Cada um dos 200 sujeitos que participam do experimento é atribuído aleatoriamente a uma de duas condições experimentais. Os indivíduos em ambas as condições realizam um teste de uma hora, que é ostensivamente uma medida de inteligência. Durante o teste, os 100 indivíduos do Grupo 1 são expostos a um ruído alto e contínuo, que, segundo eles, é devido a um gerador com defeito. Os 100 sujeitos do Grupo 2 não são expostos a nenhum ruído durante o teste. Após a conclusão desta etapa do experimento, cada sujeito, ao deixar a sala, é confrontado por um homem de meia-idade cujo braço está em uma tipóia e que trabalha no experimentado. O homem pergunta ao sujeito se estaria disposto a ajudá-lo a carregar um pacote pesado para o carro. O número de sujeitos em cada grupo que ajudam o homem é registrado. Trinta dos 100 sujeitos que foram expostos ao ruído optaram por ajudar o homem, enquanto sessenta dos 100 sujeitos que não foram expostos ao ruído optaram por ajudar o homem. Os dados indicam que o comportamento altruísta é influenciado pelo ruído?

	Ajudou	Não ajudou	Total
Barulho	30	70	100
Sem barulho	60	40	100
Total	90	110	200

dados <- matrix(c(30,60,70,40), nrow=2)
chisq.test(dados, correct = F)

## 
##  Pearson's Chi-squared test
## 
## data:  dados
## X-squared = 18.182, df = 1, p-value = 2.008e-05

chisq.test(dados, correct = T)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  dados
## X-squared = 16.99, df = 1, p-value = 3.758e-05

Exemplo 6.50 Em Python.

import numpy as np
from scipy.stats import chi2_contingency

# Dados
dados = np.array([[30, 60], [70, 40]])

# Teste qui-quadrado sem correção de Yates
chi2_stat, p_value, dof, expected = chi2_contingency(dados, correction=False)
print(f"Sem correção: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}, dof = {dof}")

# Teste qui-quadrado com correção de Yates
chi2_stat, p_value, dof, expected = chi2_contingency(dados, correction=True)
print(f"Com correção: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}, dof = {dof}")

Exemplo 6.51 (Adaptado de (Sheskin 2011, 640), teste de independência) Um pesquisador deseja testar se existe relação entre a dimensão da personalidade de introversão-extroversão e afiliação política. Duzentas pessoas são recrutadas para participar do estudo. Todos os sujeitos passam por um teste de personalidade com base no qual cada sujeito é classificado como introvertido ou extrovertido. Pede-se para cada sujeito indicar se ele ou ela é um democrata ou um republicano conforme tabela a seguir. Os dados indicam que existe uma relação significativa entre a afiliação política e se alguém é introvertido ou não extrovertido?

	Democrata	Republicano	Total
Introvertido	30	70	100
Extrovertido	60	40	100
Total	90	110	200

dados <- matrix(c(30,60,70,40), nrow=2)
chisq.test(dados, correct = F)

## 
##  Pearson's Chi-squared test
## 
## data:  dados
## X-squared = 18.182, df = 1, p-value = 2.008e-05

chisq.test(dados)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  dados
## X-squared = 16.99, df = 1, p-value = 3.758e-05

Exemplo 6.52 Em Python.

import numpy as np
from scipy.stats import chi2_contingency

# Dados
dados = np.array([[30, 60], [70, 40]])

# Teste qui-quadrado sem correção de Yates
chi2_stat, p_value, dof, expected = chi2_contingency(dados, correction=False)
print(f"Sem correção: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}, dof = {dof}")

# Teste qui-quadrado com correção de Yates
chi2_stat, p_value, dof, expected = chi2_contingency(dados, correction=True)
print(f"Com correção: chi2 = {chi2_stat:.4f}, p = {p_value:.4f}, dof = {dof}")

Exercício 6.15 Faça os cálculos dos Exemplos 6.49 e 6.51 utilizando todas as variações de estatísticas de teste.

6.3.8.5 Teste exato de Fisher para tabelas \(2 \times 2\)

Hipótese avaliada (geral)

Na(s) população(ões) representada(s) pela(s) amostra(s) em uma tabela de contingência, as frequências de células observadas são diferentes das frequências esperadas?

Hipóteses avaliadas (homogeneidade)

As \(l\) amostras são ou não homogêneas com relação à proporção de observações em cada uma das \(c\) categorias? (ou)

Se os dados forem homogêneos, a proporção de observações na \(j\)-ésima categoria será igual em todas as \(l\) populações?

Suposições

S1. Os dados avaliados representam uma amostra aleatória composta por \(n\) observações independentes.
S2. Os dados de frequência são categóricos para \(l \times c\) categorias mutuamente exclusivas.
S3. As somas das linhas e colunas (somas marginais) são predeterminadas/fixas.

Valor-p para tabelas \(2 \times 2\)

Sob \(H_0: O_{ij}=E_{ij}\) para todas as células ou \(H_0: \pi_{ij}=(\pi_{i\cdot})(\pi_{\cdot j})\) para todas as \(l \times c\) células, \[\begin{equation} P = \frac{(a+c)!(b+d)!(a+b)!(c+d)!}{n!a!b!c!d!}, \tag{6.56} \end{equation}\] onde \(a\), \(b\), \(c\) e \(d\) são as quantidades conforme tabela a seguir.

	Coluna 1	Coluna 2	Total
Linha 1	\(a\)	\(b\)	a+b
Linha 2	\(c\)	\(d\)	c+d
Total	\(a+c\)	\(b+d\)	n

Exemplo 6.53 Pode-se resolver o Exemplo 6.49 através do teste exato de Fisher.

dados <- matrix(c(30,60,70,40), nrow=2)
fisher.test(dados)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  dados
## p-value = 3.305e-05
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.1522789 0.5339334
## sample estimates:
## odds ratio 
##  0.2876339

Exemplo 6.54 Em Python.

import numpy as np
from scipy.stats import fisher_exact

# Dados
dados = np.array([[30, 60], [70, 40]])

# Teste exato de Fisher
odds_ratio, p_value = fisher_exact(dados)
print(f"Teste exato de Fisher: OR = {odds_ratio:.4f}, p = {p_value:.4f}")

Exercício 6.16 Faça os cálculos do Exemplo 6.53.

6.3.9 Paramétricos Multivariados

6.3.9.1 Análise de Variância (ANOVA) de um fator entre sujeitos

Hipótese avaliada

Em um conjunto de \(k \ge 2\) grupos independentes, há pelo menos dois com médias distintas?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. A distribuição dos dados na população subjacente da qual cada uma das amostras é derivada é normal.
S3. (Homogeneidade de variâncias) A variância da população representada pelas \(k\) amostras são iguais entre si. (\(\sigma_1^2=\sigma_2^2=\cdots=\sigma_k^2\)).

Testes relacionados

• Teste de Kruskal-Wallis de um fator entre sujeitos, Seção 6.3.12.2.
• Testes de homogeneidade de variâncias, Seção 6.3.12.1.

Estatística do teste Sob \(H_0: \mu_1=\mu_2=\cdots=\mu_k\), \[\begin{equation} F_{teste} = \frac{MQ_{EG}}{MQ_{IG}} \sim \mathcal{F}(gl_{EG},gl_{IG}), \tag{6.57} \end{equation}\]

onde \(MQ_{EG}\) é a média quadrática entre grupos dada por \[\begin{equation} MQ_{EG} = \frac{SQ_{EG}}{gl_{EG}}, \tag{6.58} \end{equation}\]

onde \(SQ_{EG}\) é a soma de quadrados entre grupos dada por \[\begin{equation} SQ_{EG} = \sum_{j=1}^k \left[ \frac{(\sum x_j)^2}{n_j} \right] - \frac{(\sum x_T)^2}{n}, \tag{6.59} \end{equation}\]

\(MQ_{IG}\) é a média quadrática intra grupos dada por \[\begin{equation} MQ_{IG} = \frac{SQ_{IG}}{gl_{IG}}, \tag{6.60} \end{equation}\]

onde \(SQ_{IG}\) é a soma de quadrados intra grupos dada por \[\begin{equation} SQ_{IG} = \sum_{j=1}^k \left[ \sum x_{j}^2 - \frac{(\sum x_j)^2}{n_j} \right], \tag{6.61} \end{equation}\]

\(gl_{EG}=k-1\) são os graus de liberdade entre grupos, \(gl_{IG}=n-k\) são os graus de liberdade intra grupos. Sabe-se também que onde \(SQ_{IG}\) é a soma de quadrados intra grupos dada por \[\begin{equation} SQ_{T} = SQ_{EG} + SQ_{IG} = \sum x_{T}^2 - \frac{(\sum x_T)^2}{n}. \tag{6.62} \end{equation}\]

Exemplo 6.55 (Adaptado de (Sheskin 2011, 886)) Um psicólogo realiza um estudo para determinar se o ruído pode ou não inibir o aprendizado. Cada um de 15 sujeitos é atribuído aleatoriamente a um dos três grupos. Cada sujeito tem 20 minutos para memorizar uma lista de 10 sílabas sem sentido, que ela diz que será testada no dia seguinte. Os cinco sujeitos atribuídos ao Grupo 1, a condição sem ruído, estudam a lista de sílabas sem sentido enquanto estão em uma sala silenciosa. Os cinco sujeitos designados para o Grupo 2, a condição de ruído moderado, estudam a lista de sílabas sem sentido enquanto ouvem música clássica. Os cinco sujeitos designados para o Grupo 3, a condição de ruído extremo, estudam a lista de sílabas sem sentido enquanto ouvem música rock. O número de sílabas sem sentido lembradas corretamente pelos 15 sujeitos segue: Grupo 1: 8,10,9,10,9; Grupo 2: 7,8,5,8,5; Grupo 3: 4,8,7,5,7. Os dados indicam que o ruído influenciou o desempenho dos sujeitos?

# dados
x <- c(8,10,9,10,9, 7,8,5,8,5, 4,8,7,5,7)
g <- as.factor(rep(1:3, each = 5))
(k <- length(unique(g))) # número de grupos

## [1] 3

boxplot(x ~ g)

# validando suposições, veja ?by
by(x,g,shapiro.test)  # S2, normalidade

## g: 1
## 
##  Shapiro-Wilk normality test
## 
## data:  dd[x, ]
## W = 0.88104, p-value = 0.314
## 
## -------------------------------------------------------------------------------------- 
## g: 2
## 
##  Shapiro-Wilk normality test
## 
## data:  dd[x, ]
## W = 0.80299, p-value = 0.08569
## 
## -------------------------------------------------------------------------------------- 
## g: 3
## 
##  Shapiro-Wilk normality test
## 
## data:  dd[x, ]
## W = 0.91367, p-value = 0.4899

car::leveneTest(x,g)  # S3, homogeneidade de variâncias via Levene

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  0.6667 0.5314
##       12

stats::fligner.test(x,g)  # S3, homogeneidade de variâncias via Fligner-Killeen

## 
##  Fligner-Killeen test of homogeneity of variances
## 
## data:  x and g
## Fligner-Killeen:med chi-squared = 1.5375, df = 2, p-value = 0.4636

# cálculos
(soma <- by(x,g,sum))     # soma por grupo

## g: 1
## [1] 46
## -------------------------------------------------------------------------------------- 
## g: 2
## [1] 33
## -------------------------------------------------------------------------------------- 
## g: 3
## [1] 31

(media <- by(x,g,mean))   # média por grupo

## g: 1
## [1] 9.2
## -------------------------------------------------------------------------------------- 
## g: 2
## [1] 6.6
## -------------------------------------------------------------------------------------- 
## g: 3
## [1] 6.2

(soma2 <- by(x^2,g,sum))  # soma ao quadrado por grupo

## g: 1
## [1] 426
## -------------------------------------------------------------------------------------- 
## g: 2
## [1] 227
## -------------------------------------------------------------------------------------- 
## g: 3
## [1] 203

(n <- by(x,g,length))     # tamanho da amostra por grupo

## g: 1
## [1] 5
## -------------------------------------------------------------------------------------- 
## g: 2
## [1] 5
## -------------------------------------------------------------------------------------- 
## g: 3
## [1] 5

(somaT <- sum(soma))      # soma total

## [1] 110

(soma2T <- sum(soma2))    # soma ao quadrado total

## [1] 856

(nT <- sum(n))            # tamanho total da amostra

## [1] 15

(sqt <- soma2T - somaT^2/nT) # SQ_T pela Eq. (3.50)

## [1] 49.33333

(sqeg <- sum(soma^2/n) - somaT^2/nT) # SQ_{EG} pela Eq. (3.47)

## [1] 26.53333

(sqig <- sum(soma2 - soma^2/n)) # SQ_{IG} pela Eq. (3.49)

## [1] 22.8

sqt - sqeg # SQ_{IG} pela Eq. (3.50)

## [1] 22.8

(gleg <- k-1) # gl_{EG}

## [1] 2

(glig <- nT-k) # gl_{IG}

## [1] 12

(mqeg <- sqeg/gleg) # MQ_{EG} pela Eq. (3.46)

## [1] 13.26667

(mqig <- sqig/glig) # MQ_{IG} pela Eq. (3.48)

## [1] 1.9

(Ft <- mqeg/mqig) # estatística do teste pela Eq. (3.45)

## [1] 6.982456

2*df(Ft,gleg,glig)

## [1] 0.009007219

# pela função aov
summary(anova1 <- aov(x ~ g))

##             Df Sum Sq Mean Sq F value  Pr(>F)   
## g            2  26.53   13.27   6.982 0.00974 **
## Residuals   12  22.80    1.90                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1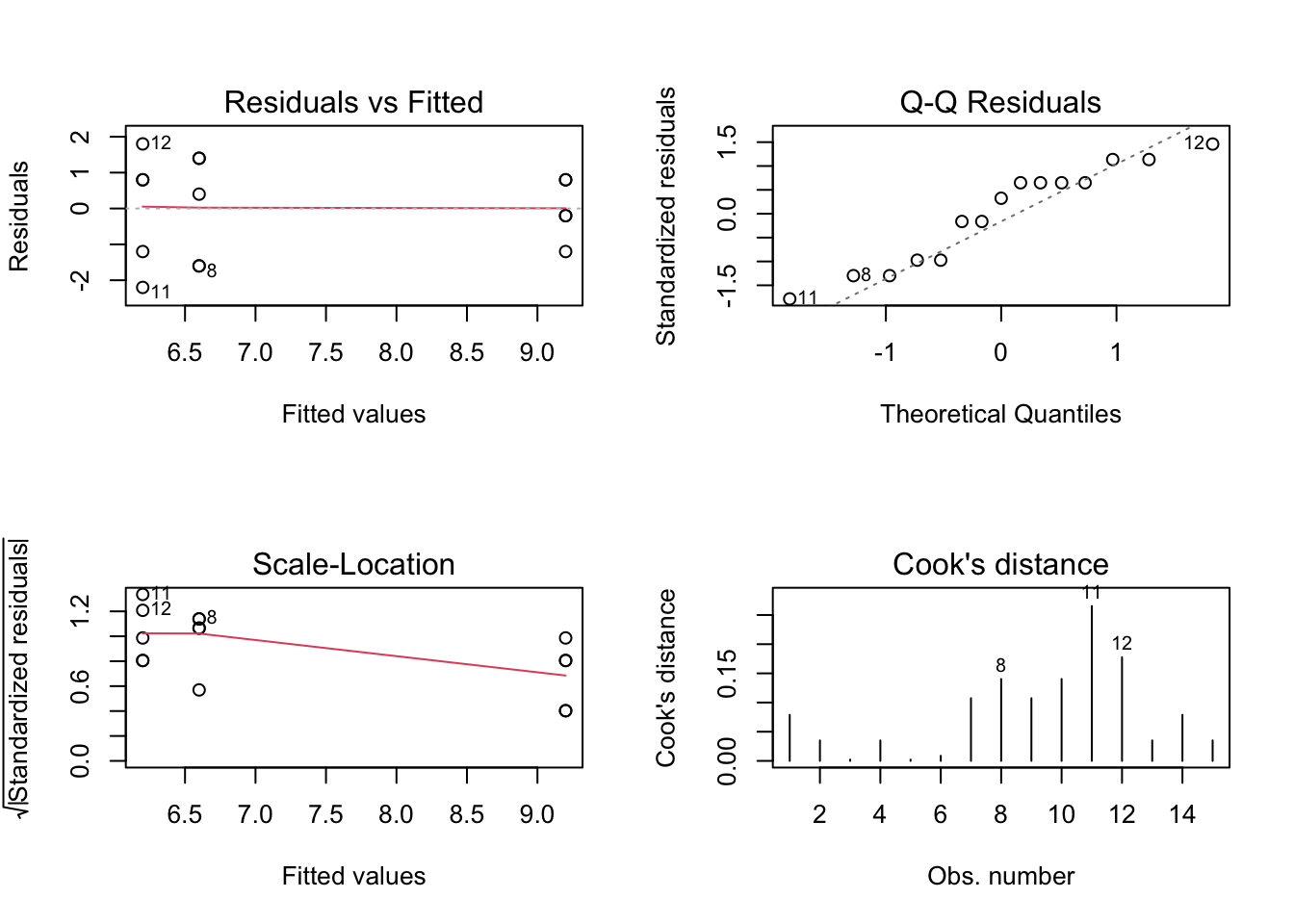

par(mfrow=c(2,2))
plot(anova1, which=1:4)

# pela função anova
anova(lm(x ~ g))

## Analysis of Variance Table
## 
## Response: x
##           Df Sum Sq Mean Sq F value   Pr(>F)   
## g          2 26.533  13.267  6.9825 0.009745 **
## Residuals 12 22.800   1.900                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# pela função car::Anova
car::Anova(lm(x ~ g))

## Anova Table (Type II tests)
## 
## Response: x
##           Sum Sq Df F value   Pr(>F)   
## g         26.533  2  6.9825 0.009745 **
## Residuals 22.800 12                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# pela função lm
summary(lm(x ~ g))

## 
## Call:
## lm(formula = x ~ g)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##   -2.2   -1.2    0.4    0.8    1.8 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   9.2000     0.6164  14.924 4.12e-09 ***
## g2           -2.6000     0.8718  -2.982  0.01143 *  
## g3           -3.0000     0.8718  -3.441  0.00488 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.378 on 12 degrees of freedom
## Multiple R-squared:  0.5378, Adjusted R-squared:  0.4608 
## F-statistic: 6.982 on 2 and 12 DF,  p-value: 0.009745

# Post-hoc
stats::TukeyHSD(anova1)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = x ~ g)
## 
## $g
##     diff      lwr        upr     p adj
## 2-1 -2.6 -4.92579 -0.2742104 0.0286083
## 3-1 -3.0 -5.32579 -0.6742104 0.0125541
## 3-2 -0.4 -2.72579  1.9257896 0.8914526

rstatix::tukey_hsd(anova1)

## # A tibble: 3 × 9
##   term  group1 group2 null.value estimate conf.low conf.high  p.adj p.adj.signif
## * <chr> <chr>  <chr>       <dbl>    <dbl>    <dbl>     <dbl>  <dbl> <chr>       
## 1 g     1      2               0   -2.6      -4.93    -0.274 0.0286 *           
## 2 g     1      3               0   -3        -5.33    -0.674 0.0126 *           
## 3 g     2      3               0   -0.400    -2.73     1.93  0.891  ns

Exemplo 6.56 Em Python.

import numpy as np
import pandas as pd
from scipy.stats import shapiro, levene, f
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import matplotlib.pyplot as plt

# Dados
x = np.array([8, 10, 9, 10, 9, 7, 8, 5, 8, 5, 4, 8, 7, 5, 7])
g = np.array([1] * 5 + [2] * 5 + [3] * 5)

# Convertendo para DataFrame do pandas
df = pd.DataFrame({'x': x, 'g': g})

# Validando suposições
# Normalidade
for group in df['g'].unique():
    stat, p_value = shapiro(df['x'][df['g'] == group])
    print(f"Shapiro-Wilk do grupo {group}: estat = {stat:.4f}, p-valor = {p_value:.4f}")

# Homogeneidade de variâncias
stat, p_value = levene(*[df['x'][df['g'] == group] for group in df['g'].unique()])
print(f"Levene: estat = {stat:.4f}, p-valor = {p_value:.4f}")

# Cálculos
k = len(np.unique(g))  # número de grupos

# Soma por grupo
soma = df.groupby('g')['x'].sum()

# Média por grupo
media = df.groupby('g')['x'].mean()

# Soma dos quadrados por grupo
soma2 = df.groupby('g')['x'].apply(lambda x: np.sum(x**2))

# Tamanho da amostra por grupo
n = df.groupby('g')['x'].count()

# Soma total
somaT = np.sum(soma)

# Soma dos quadrados total
soma2T = np.sum(soma2)

# Tamanho total da amostra
nT = np.sum(n)

# SQ_T
sqt = soma2T - somaT**2 / nT

# SQ_EG
sqeg = np.sum(soma**2 / n) - somaT**2 / nT

# SQ_IG
sqig = np.sum(soma2 - soma**2 / n)

# Verificando SQ_IG
assert np.isclose(sqt - sqeg, sqig)

# gl_EG
gleg = k - 1

# gl_IG
glig = nT - k

# MQ_EG
mqeg = sqeg / gleg

# MQ_IG
mqig = sqig / glig

# Estatística F
Ft = mqeg / mqig

# p-value
p_value_manual = 2 * f.sf(Ft, dfn=gleg, dfd=glig)

print(f"\nEstatística F (manual): {Ft:.4f}")
print(f"p-value (manual): {p_value_manual:.4f}")

# ANOVA usando statsmodels
model = smf.ols('x ~ C(g)', data=df).fit()
anova_table = model.summary().tables[0]
print("\nTabela ANOVA (statsmodels):")
print(anova_table)

# Diagnóstico dos resíduos
fig, axs = plt.subplots(2, 2, figsize=(10, 8))
axs[0, 0].scatter(model.fittedvalues, model.resid)
axs[0, 0].set_xlabel("Valores Ajustados")
axs[0, 0].set_ylabel("Resíduos")
axs[0, 0].set_title("Resíduos vs. Valores Ajustados")

axs[0, 1].hist(model.resid, bins='auto', color='lightgray', 
               edgecolor='black')
axs[0, 1].set_title("Histograma dos Resíduos")
axs[0, 1].set_xlabel("Resíduos")
axs[0, 1].set_ylabel("Frequência")

# QQ plot dos resíduos (requer statsmodels.api)
import statsmodels.api as sm
sm.qqplot(model.resid, line='s', ax=axs[1, 0])
axs[1, 0].set_title("QQ Plot dos Resíduos")

# Teste de Shapiro-Wilk para os resíduos
stat, p_value = shapiro(model.resid)
axs[1, 1].text(0.5, 0.5, 
               f"Shapiro-Wilk: estatística = {stat:.4f}, p = {p_value:.4f}", 
               horizontalalignment='center', verticalalignment='center', 
               transform=axs[1, 1].transAxes)
axs[1, 1].axis('off')

plt.tight_layout()
plt.show()

# Post-hoc Tukey HSD
tukey_result = pairwise_tukeyhsd(df['x'], df['g'])
print("\nTeste Post-Hoc de Tukey HSD:")
print(tukey_result)

Exercício 6.17 (Adaptado de (DeGroot and Schervish 2012, 754)) Moore e McCabe (1999) descrevem dados coletados em Consumer Reports (junho de 1986, pp. 364-67). Os dados incluem (entre outras coisas) calorias conteúdo de 63 marcas de salsichas de cachorros-quentes conforme tabela a seguir. A salsichas vêm em quatro variedades: carne bovina, carne (?), aves e especialidades. É interessante saber se, e em que medida, as diferentes variedades diferem em seus conteúdos calóricos. Realize o procedimento de análise de variância e post hoc, indicando se há diferença significativa entre os grupos.

Carne bovina 186, 181, 176, 149, 184, 190, 158, 139, 175, 148, 152, 111, 141, 153, 190, 157, 131, 149, 135, 132
Carne 173, 191, 182, 190, 172, 147, 146, 139, 175, 136, 179, 153,107, 195, 135, 140, 138
Aves 129, 132, 102, 106, 94, 102, 87, 99, 107, 113, 135, 142, 86, 143, 152, 146, 144
Especialidades 155, 170, 114, 191, 162, 146, 140, 187, 180

# Dica
g <- as.factor(rep(1:4, times = c(20,17,17,9)))
x <- c(186, 181, 176, 149, 184, 190, 158, 139, 175, 148, 152, 111,
       141, 153, 190, 157, 131, 149, 135, 132, 173, 191, 182, 190, 
       172, 147, 146, 139, 175, 136, 179, 153, 107, 195, 135, 140, 
       138, 129, 132, 102, 106, 94, 102, 87, 99, 107, 113, 135, 
       142, 86, 143, 152, 146, 144, 155, 170, 114, 191, 162, 146, 
       140, 187, 180)
boxplot(x ~ g)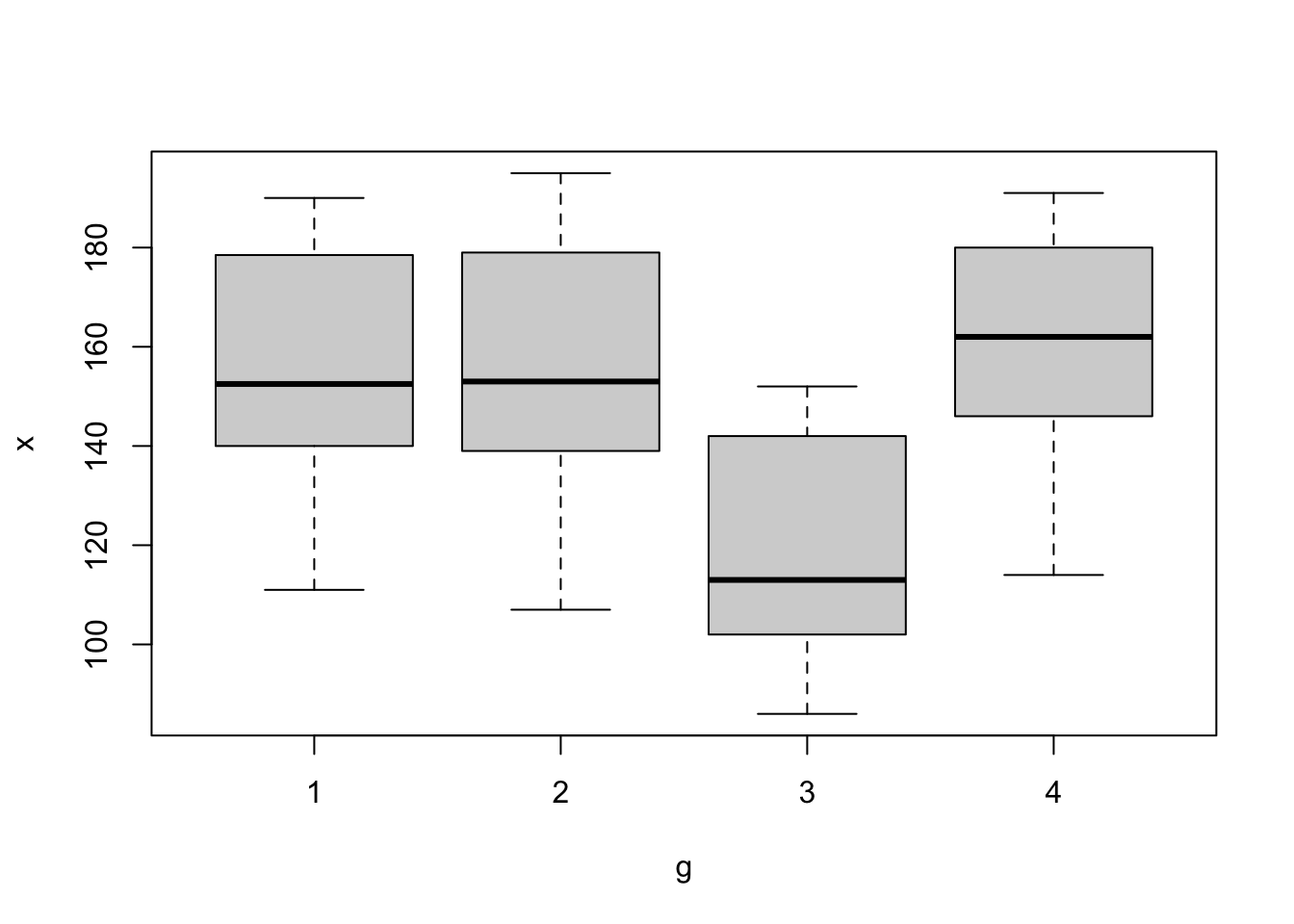

Exemplo 6.57 Em Python.

import numpy as np
import matplotlib.pyplot as plt

# Dados
g = np.array([1] * 20 + [2] * 17 + [3] * 17 + [4] * 9)
x = np.array([186, 181, 176, 149, 184, 190, 158, 139, 175, 148, 
              152, 111, 141, 153, 190, 157, 131, 149, 135, 132, 
              173, 191, 182, 190, 172, 147, 146, 139, 175, 136, 
              179, 153, 107, 195, 135, 140, 138, 129, 132, 102, 
              106, 94, 102, 87, 99, 107, 113, 135, 142, 86, 143, 
              152, 146, 144, 155, 170, 114, 191, 162, 146, 140, 
              187, 180])

# Criando o boxplot
plt.boxplot([x[g == i] for i in np.unique(g)])
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.title('Boxplot de x por grupo')
plt.xticks(np.arange(1, len(np.unique(g)) + 1), np.unique(g))
plt.show()

6.3.10 Não Paramétricos Univariados

6.3.10.1 Teste dos postos sinalizados de Wilcoxon para uma amostra

Hipótese avaliada

Uma amostra de \(n\) sujeitos (ou objetos) vem de uma população em que a mediana \(\theta\) é igual a um valor especificado?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. As pontuações originais obtidas para cada um dos sujeitos/objetos são quantitativas.
S3. A distribuição da população subjacente é simétrica.

Testes relacionados

• Teste \(z\) para média de uma amostra, Seção 6.3.7.1.
• Teste \(t\) para média de uma amostra, Seção 6.3.7.2.

Para testar a simetria foi considerada a função symmetry_test() do pacote symmetry (Ivanović, Milošević, and Obradović 2023). Segundo (Milošević and Obradović 2018, 4), entre os testes originalmente destinados a testar simetria em torno de uma média desconhecida, o mais famoso é o teste clássico \(\sqrt{b_1}\), baseado no coeficiente de assimetria da amostra, com estatística de teste \(\sqrt{b_1} = m_3/s^3\) onde \(m_3\) é o terceiro momento central da amostra conforme numerador da Eq. (2.41), e \(s\) é o desvio padrão amostral conforme Eq. (2.36).

# dados
set.seed(456); z <- rnorm(100) # N(0,1)
# verificando suposição S3 (simetria)
library(symmetry)
set.seed(111); symmetry_test(z, 'B1')  # √b1

## 
##  Symmetry test
##  Null hypothesis: Data is symmetric
## 
## data:  z
## B1 = -0.00024191, B = 1000, p-value = 0.998
## sample estimates:
##        mu 
## 0.1205748

# teste de Wilcoxon
wilcox.test(z, mu = 0) # mediana 0

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  z
## V = 2851, p-value = 0.2631
## alternative hypothesis: true location is not equal to 0

wilcox.test(z, mu = 1) # mediana 1

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  z
## V = 563, p-value = 1.538e-11
## alternative hypothesis: true location is not equal to 1

Exemplo 6.58 Em Python.

import numpy as np
from scipy.stats import wilcoxon, skewtest

# Dados
np.random.seed(456)
z = np.random.normal(size=100)

# Verificando a suposição de simetria (similar ao symmetry_test com 'B1')
# Usando o teste de assimetria de Pearson
statistic, p_value = skewtest(z)
print(f"Teste de assimetria: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# Teste de Wilcoxon
# Mediana 0
statistic, p_value = wilcoxon(z)
print(f"\nTeste de Wilcoxon (mediana = 0): estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# Mediana 1
statistic, p_value = wilcoxon(z, y=np.ones_like(z))  # Comparando com um array de 1s
print(f"Teste de Wilcoxon (mediana = 1): estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

6.3.10.2 Teste de aderência de Shapiro-Wilk para uma amostra

Hipótese avaliada

Os dados têm distribuição normal?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. A escala de mensuração é quantitativa.

Exemplo 6.59 Exemplo adaptado da documentação de stats::shapiro.test().

set.seed(8765); z <- rnorm(100, mean = 5, sd = 3)
shapiro.test(z)

## 
##  Shapiro-Wilk normality test
## 
## data:  z
## W = 0.98521, p-value = 0.3287

set.seed(7654); u <- runif(100, min = 4, max = 6)
shapiro.test(u)

## 
##  Shapiro-Wilk normality test
## 
## data:  u
## W = 0.95686, p-value = 0.002415

Exemplo 6.60 Em Python.

import numpy as np
from scipy.stats import shapiro, norm

# Gerando dados da distribuição normal
np.random.seed(8765)
z = norm.rvs(loc=5, scale=3, size=100)

# Teste de Shapiro-Wilk para z
stat, p_value = shapiro(z)
print(f"Teste de Shapiro-Wilk para z: estatística = {stat:.4f}, p-valor = {p_value:.4f}")

# Gerando dados da distribuição uniforme
np.random.seed(7654)
u = np.random.uniform(low=4, high=6, size=100)

# Teste de Shapiro-Wilk para u
stat, p_value = shapiro(u)
print(f"Teste de Shapiro-Wilk para u: estatística = {stat:.4f}, p-valor = {p_value:.4f}")

6.3.11 Não Paramétricos Bivariados

6.3.11.1 Teste de Kolmogorov-Smirnov para duas amostras independentes

Hipótese avaliada

Duas amostras independentes representam duas populações distintas?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. A escala de mensuração é pelo menos ordinal.

Estatística do teste \[\begin{equation} D = \sup_x |F_{1,n}(x) - F_{2,m}(x)| \tag{6.63} \end{equation}\]

onde \(F_{1,n}(x)\) e \(F_{2,m}(x)\) são respectivamente as funções distribuição acumuladas empíricas das distribuições 1 e 2 e \(\sup\) é a função supremo.

Exemplo 6.61 Exemplo adaptado da documentação de stats::ks.test().

set.seed(99); x <- rnorm(50)
set.seed(88); y <- runif(30)
ks.test(x, y)

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x and y
## D = 0.52, p-value = 3.885e-05
## alternative hypothesis: two-sided

set.seed(77); z <- runif(30)
ks.test(x, z)

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x and z
## D = 0.54667, p-value = 1.178e-05
## alternative hypothesis: two-sided

ks.test(y, z)

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  y and z
## D = 0.16667, p-value = 0.808
## alternative hypothesis: two-sided

Exemplo 6.62 Em Python.

import numpy as np
from scipy.stats import ks_2samp

# Gerando dados
np.random.seed(99)
x = np.random.normal(size=50)
np.random.seed(88)
y = np.random.uniform(size=30)
np.random.seed(77)
z = np.random.uniform(size=30)

# Testes de Kolmogorov-Smirnov
statistic, p_value = ks_2samp(x, y)
print(f"Teste KS para x e y: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

statistic, p_value = ks_2samp(x, z)
print(f"Teste KS para x e z: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

statistic, p_value = ks_2samp(y, z)
print(f"Teste KS para y e z: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

6.3.11.2 Teste dos postos de Mann-Whitney para amostras independentes

Hipótese avaliada

Duas amostras independentes representam duas populações com medianas diferentes?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. As duas amostras são independentes entre si.
S3. Os dados são ordinais ou quantitativos.
S4. As distribuições de onde as amostras foram retiradas possuem mesma forma.

Testes relacionados

• Teste \(t\) para médias de duas amostras independentes, Seção 6.3.8.2.

Exemplo 6.63 (Adaptado de (Sheskin 2011, 532)) Para avaliar a eficácia de um novo medicamento antidepressivo, dez pacientes com depressão clínica são aleatoriamente designados para um dos dois grupos. Cinco pacientes são atribuídos ao Grupo 1, onde é administrado o antidepressivo por um período de seis meses. Os outros cinco pacientes são atribuídos ao Grupo 2, que recebe um placebo durante o mesmo período de seis meses. Suponha que, antes de introduzir os tratamentos experimentais, o experimentador confirmou que o nível de depressão nos dois grupos era igual. Após seis meses, todos os dez sujeitos são avaliados por um psiquiatra (que é cego em relação à condição experimental do sujeito) quanto ao nível de depressão. As classificações de depressão do psiquiatra para os cinco sujeitos em cada grupo seguem (quanto mais alta a classificação, mais deprimido é o sujeito): Grupo 1: 11, 1,0, 2, 0; Grupo 2: 11, 11, 5, 8, 4. Os dados indicam que o antidepressivo é eficaz?

\[\left\{ \begin{array}{l} H_0: \theta_1 \ge \theta_2 \equiv \theta_1 - \theta_2 \ge 0 \; \text{(tratamento igual ou menos eficaz que o placebo)} \\ H_1: \theta_1 < \theta_2 \equiv \theta_1 - \theta_2 < 0 \; \text{(tratamento mais eficaz que o placebo)} \\ \end{array} \right. \]

x <- c(11,1,0,2,0)
y <- c(11,11,5,8,4)
median(x); median(y)

## [1] 1

## [1] 8

# avaliando S4
ks.test(x,y)

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x and y
## D = 0.8, p-value = 0.07937
## alternative hypothesis: two-sided

wilcox.test(x, y, alternative  = 'less')

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  x and y
## W = 4, p-value = 0.04484
## alternative hypothesis: true location shift is less than 0

Exemplo 6.64 Em Python.

import numpy as np
from scipy.stats import ks_2samp, mannwhitneyu

# Dados
x = np.array([11, 1, 0, 2, 0])
y = np.array([11, 11, 5, 8, 4])

# Calculando as medianas
print(f"Mediana de x: {np.median(x)}")  # Output: 1.0
print(f"Mediana de y: {np.median(y)}")  # Output: 5.0

# Avaliando a suposição S4 (distribuições semelhantes)
statistic, p_value = ks_2samp(x, y)
print(f"\nTeste KS para x e y: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# Teste de Mann-Whitney U (similar ao teste de Wilcoxon para duas amostras independentes)
statistic, p_value = mannwhitneyu(x, y, alternative='less')
print(f"Teste de Mann-Whitney U (x < y): estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

6.3.11.3 Teste dos postos de Wilcoxon para amostras dependentes/pareadas

Hipótese avaliada

Duas amostras dependentes representam duas populações distintas?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. As pontuações originais obtidas para cada um dos sujeitos/objetos são quantitativas.
S3. A distribuição dos escores de diferença nas populações representadas pelas duas amostras é simétrica em relação à mediana da população de escores de diferença.

Testes relacionados

• Teste \(t\) para médias de duas amostras dependentes/pareadas, Seção 6.3.8.3.

Assim como no teste dos postos sinalizados de Wilcoxon para uma amostra (Seção 6.3.10.1), foi considerada a estatística \(\sqrt{b_1}\) da função symmetry::symmetry_test() para testar a simetria.

Exemplo 6.65 Exemplo adaptado da documentação de stats::wilcox.test().

# dados
x <- c(1.83,  0.50,  1.62,  2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)
median(x-y)

## [1] 0.49

# verificando suposição S3 (simetria da diferença em relação à mediana)
set.seed(111)
symmetry::symmetry_test(x-y, 'B1', mu = median(x-y))  # √b1

## 
##  Symmetry test
##  Null hypothesis: Data is symmetric around 0.49
## 
## data:  x - y
## B1 = -0.066026, B = 1000, p-value = 0.874

# teste de Wilcoxon para amostras pareadas
wilcox.test(x, y, paired = TRUE, alternative = 'greater')

## 
##  Wilcoxon signed rank exact test
## 
## data:  x and y
## V = 40, p-value = 0.01953
## alternative hypothesis: true location shift is greater than 0

Exemplo 6.66 Em Python.

import numpy as np
from scipy.stats import wilcoxon, skewtest

# Dados
x = np.array([1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30])
y = np.array([0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29])

# Calculando a mediana da diferença
diff = x - y
median_diff = np.median(diff)
print(f"Mediana de (x - y): {median_diff:.4f}")  # Output: 0.4900

# Verificando a suposição de simetria (similar ao symmetry_test com 'B1')
# Usando o teste de assimetria de Pearson
statistic, p_value = skewtest(diff)
print(f"\nTeste de assimetria: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# Teste de Wilcoxon para amostras pareadas
statistic, p_value = wilcoxon(x, y, alternative='greater')
print(f"\nTeste de Wilcoxon para amostras pareadas (x > y): estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

6.3.11.4 Teste de McNemar para amostras dependentes/pareadas

Hipótese avaliada

Duas amostras dependentes representam duas populações distintas?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. As variáveis são binárias e categóricas (ordinais ou nominais).
S3. Cada um dos \(n\) sujeitos (ou \(n\) pares de sujeitos combinados) contribui com duas pontuações na variável dependente.

Estatística do teste

Sob \(H_0:\pi_{12}=\pi_{21}\), \[\begin{equation} \chi_{teste}^2 = \frac{(n_{12}-n_{21})^2}{n_{12}+n_{21}} \sim \chi^2(1) \tag{6.64} \end{equation}\] onde \(n_{12}\) indica o número de elementos da linha 1, coluna 2 da tabela e \(n_{21}\) indica o número de elementos da linha 2, coluna e \(\chi^2(1)\) indica a distribuição qui-quadrado com 1 grau de liberdade.

Estatística do teste com correção de continuidade

Sob \(H_0:\pi_{12}=\pi_{21}\), \[\begin{equation} \chi_{teste}^2 = \frac{(|n_{12}-n_{21}|-1)^2}{n_{12}+n_{21}} \sim \chi^2(1) \tag{6.65} \end{equation}\]

Valor-p

Sob \(H_0: \pi_{12}=\pi_{21}\), \[\begin{equation} \text{Valor-p} = P(\chi^2 \ge \chi_{teste}^2). \tag{6.66} \end{equation}\]

Exemplo 6.67 (Exemplo adaptado da documentação de mcnemar.test()) A aprovação do desempenho do Presidente no cargo foi realizado em duas pesquisas, com um mês de intervalo, para uma amostra aleatória de 1600 estadunidenses em idade de votar. Os dados indicam uma mudança de percepção em relação às duas pesquisas?

# dados
ad <- c('Aprova', 'Desaprova')
dat <- matrix(c(794, 86, 150, 570), nrow = 2,
              dimnames = list('1ª pesquisa' = ad,
                              ' 2ª pesquisa' = ad))
dat

##             2ª pesquisa
## 1ª pesquisa Aprova Desaprova
##   Aprova       794       150
##   Desaprova     86       570

# usando a estatística do teste sem correção
(qui <- (dat[1,2]-dat[2,1])^2/(dat[1,2]+dat[2,1]))

## [1] 17.35593

# valor-p
1-pchisq(qui,1)

## [1] 3.099293e-05

# teste via mcnemar.test
mcnemar.test(dat, correct = FALSE)

## 
##  McNemar's Chi-squared test
## 
## data:  dat
## McNemar's chi-squared = 17.356, df = 1, p-value = 3.099e-05

# usando a estatística do teste com correção
(qui.c <- (abs(dat[1,2]-dat[2,1])-1)^2/(dat[1,2]+dat[2,1]))

## [1] 16.8178

# valor-p
1-pchisq(qui.c,1)

## [1] 4.114562e-05

# teste via mcnemar.test
mcnemar.test(dat, correct = TRUE)

## 
##  McNemar's Chi-squared test with continuity correction
## 
## data:  dat
## McNemar's chi-squared = 16.818, df = 1, p-value = 4.115e-05

Exemplo 6.68 Em Python.

import numpy as np
from scipy.stats import chi2
from statsmodels.stats.contingency_tables import mcnemar

# Dados
dat = np.array([[794, 86], [150, 570]])

# Estatística do teste sem correção
qui = (dat[0, 1] - dat[1, 0])**2 / (dat[0, 1] + dat[1, 0])
print(f"Estatística qui-quadrado (sem correção): {qui:.4f}")  # Output: 34.6933

# Valor-p
p_value = 1 - chi2.cdf(qui, df=1)
print(f"p-value (sem correção): {p_value:.4f}") # Output: 0.0000

# Teste de McNemar sem correção
chi2_stat, p_value = mcnemar(dat, exact=False, correction=False)
print(f"\nTeste de McNemar (sem correção): chi2 = {chi2_stat:.4f}, p = {p_value:.4f}")

# Estatística do teste com correção
qui_c = (abs(dat[0, 1] - dat[1, 0]) - 1)**2 / (dat[0, 1] + dat[1, 0])
print(f"\nEstatística qui-quadrado (com correção): {qui_c:.4f}")  # Output: 33.0478

# Valor-p
p_value_c = 1 - chi2.cdf(qui_c, df=1)
print(f"p-value (com correção): {p_value_c:.4f}")  # Output: 0.0000

# Teste de McNemar com correção
chi2_stat_c, p_value_c = mcnemar(dat, exact=False, correction=True)
print(f"\nTeste de McNemar (com correção): chi2 = {chi2_stat_c:.4f}, p = {p_value_c:.4f}")

Exercício 6.18 (Adaptado de (Sheskin 2011, 837)) Um pesquisador conduz um estudo para investigar se uma série semanal de televisão altamente crítica quanto ao uso de animais em pesquisas médicas influencia a opinião pública. Cem sujeitos selecionados aleatoriamente são avaliados por um teste para determinar sua atitude em relação ao uso de animais em pesquisas médicas. Com base em suas respostas, os sujeitos são então categorizados como pró-pesquisa com animais ou anti-pesquisa com animais. Após o pré-teste, todos os sujeitos são orientados a assistir à série de televisão (com duração de dois meses). Na conclusão da série, a atitude de cada sujeito em relação à pesquisa animal é reavaliada. Os resultados do estudo estão resumidos na tabela a seguir. Os dados indicam que uma mudança de atitude em relação à pesquisa com animais ocorreu depois que os participantes assistiram à série de televisão? Resolva utilizando as estatísticas com e sem correção de continuidade, realizando os cálculos e também aplicando a função stats::mcnemar.test().

	Pós-teste
Pré-teste	Anti	Pró	Total
Anti	10	13	23
Pró	41	36	77
Total	51	49	100

dados <- matrix(c(10,41,13,36), nrow = 2,
                dimnames = list('Pré-teste' = c('Anti', 'Pró'),
                                'Pós-teste' = c('Anti', 'Pró')))
dados

##          Pós-teste
## Pré-teste Anti Pró
##      Anti   10  13
##      Pró    41  36

mcnemar.test(dados)

## 
##  McNemar's Chi-squared test with continuity correction
## 
## data:  dados
## McNemar's chi-squared = 13.5, df = 1, p-value = 0.0002386

Exemplo 6.69 Em Python.

import numpy as np
from statsmodels.stats.contingency_tables import mcnemar

# Dados
dados = np.array([[10, 41], [13, 36]])

# Teste de McNemar com correção de continuidade (padrão)
chi2_stat, p_value = mcnemar(dados, exact=False, correction=True)
print(f"Teste de McNemar: chi2={chi2_stat:.4f}, p={p_value:.4f}")

6.3.12 Não Paramétricos Multivariados

6.3.12.1 Testes de homogeneidade de variâncias

Tests for homogeneity of variances are often of interest as a preliminary to other analyses such as analysis of variance or a pooling of data from different sources to yield an improved estimated variance. (Conover, Johnson, and Johnson 1981, 351)

(Conover, Johnson, and Johnson 1981, 360) examinam testes paramétricos e não paramétricos de homogeneidade de variâncias, indicando que “parece razoável recomendar Lev1:med (Levene 1960), (Brown and Forsythe 1974), F-K:med \(chi^2\) e F-K:med \(F\) (Fligner and Killeen 1976) como testes robustos e poderosos para variâncias quando as médias da população são desconhecidas”.

Teste	R	Python
Levene	car::leveneTest()	scipy.stats.levene()
Fligner-Killeen	stats::fligner.test()	scipy.stats.fligner()

Exemplo 6.70 Exemplos baseados nas documentações de car::leveneTest e stats::fligner.test.

library(car)

# Banco de dados Moore
by(Moore$conformity, Moore$fcategory, var)

## Moore$fcategory: high
## [1] 33.78095
## -------------------------------------------------------------------------------------- 
## Moore$fcategory: low
## [1] 27.49524
## -------------------------------------------------------------------------------------- 
## Moore$fcategory: medium
## [1] 24.82857

car::leveneTest(Moore$conformity, Moore$fcategory)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2   0.046 0.9551
##       42

stats::fligner.test(Moore$conformity, Moore$fcategory)

## 
##  Fligner-Killeen test of homogeneity of variances
## 
## data:  Moore$conformity and Moore$fcategory
## Fligner-Killeen:med chi-squared = 0.081959, df = 2, p-value = 0.9598

# Banco de dados InsectSprays
by(InsectSprays$count, InsectSprays$spray, var)

## InsectSprays$spray: A
## [1] 22.27273
## -------------------------------------------------------------------------------------- 
## InsectSprays$spray: B
## [1] 18.24242
## -------------------------------------------------------------------------------------- 
## InsectSprays$spray: C
## [1] 3.901515
## -------------------------------------------------------------------------------------- 
## InsectSprays$spray: D
## [1] 6.265152
## -------------------------------------------------------------------------------------- 
## InsectSprays$spray: E
## [1] 3
## -------------------------------------------------------------------------------------- 
## InsectSprays$spray: F
## [1] 38.60606

car::leveneTest(InsectSprays$count, InsectSprays$spray)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value   Pr(>F)   
## group  5  3.8214 0.004223 **
##       66                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

stats::fligner.test(InsectSprays$count, InsectSprays$spray)

## 
##  Fligner-Killeen test of homogeneity of variances
## 
## data:  InsectSprays$count and InsectSprays$spray
## Fligner-Killeen:med chi-squared = 14.483, df = 5, p-value = 0.01282

Exemplo 6.71 Em Python.

import pandas as pd
import numpy as np
from scipy.stats import levene, fligner

# Moore dataset (assuming you have this data in a pandas DataFrame 
# called 'Moore') If you don't have it readily available, you'll 
# need to load it. A common way is from a CSV.
# Example: Moore = pd.read_csv("moore.csv")

# Calculate variance for each group
variances_moore = Moore.groupby('fcategory')['conformity'].var()
print("Variances (Moore):\n", variances_moore)

# Levene's test
levene_result_moore = levene(Moore['conformity'], 
                           *[Moore['conformity'][Moore['fcategory'] == cat] for cat in Moore['fcategory'].unique()])
print("\nLevene's test (Moore):\n", levene_result_moore)

# Fligner's test
fligner_result_moore = fligner(Moore['conformity'], 
                             *[Moore['conformity'][Moore['fcategory'] == cat] for cat in Moore['fcategory'].unique()])
print("\nFligner's test (Moore):\n", fligner_result_moore)


# InsectSprays dataset (this dataset is available within the pydataset library)
try:
    from pydataset import data
    InsectSprays = data('InsectSprays')
except ImportError:
    print("pydataset not found. Install it using: pip install pydataset")
    exit() # or handle the error in another way

# Calculate variance for each group
variances_insect = InsectSprays.groupby('spray')['count'].var()
print("\nVariances (InsectSprays):\n", variances_insect)

# Levene's test
levene_result_insect = levene(InsectSprays['count'], 
                            *[InsectSprays['count'][InsectSprays['spray'] == sp] for sp in InsectSprays['spray'].unique()])
print("\nLevene's test (InsectSprays):\n", levene_result_insect)

# Fligner's test
fligner_result_insect = fligner(InsectSprays['count'], 
                              *[InsectSprays['count'][InsectSprays['spray'] == sp] for sp in InsectSprays['spray'].unique()])
print("\nFligner's test (InsectSprays):\n", fligner_result_insect)

Exercício 6.19 Veja

1. https://rdrr.io/cran/car/man/leveneTest.html.
2. https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.levene.html.
3. https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/fligner.test.
4. https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.fligner.html.
5. Teste F (de Hartley) de igualdade de variâncias, (H. O. Hartley 1950), stats::var.test().
6. Teste de Bartlett, (Bartlett 1937), bartlett.test().
7. Teste de Brown–Forsythe, (Brown and Forsythe 1974), onewaytests::bf.test().

6.3.12.2 Teste de Kruskal-Wallis de um fator entre sujeitos

Hipótese avaliada

Em um conjunto de \(k \ge 2\) grupos independentes, há pelo menos dois com medianas distintas?

Suposições

S1. Cada amostra foi selecionada aleatoriamente da população que representa.
S2. As \(k\) amostras são independentes umas das outras.
S3. A variável dependente (que é subsequentemente classificada) é uma variável aleatória contínua.
S4. As distribuições subjacentes das quais as amostras são derivadas possuem a mesma forma, não obrigatoriamente normais.

Testes relacionados

• Análise de Variância (ANOVA) de um fator entre sujeitos, Seção 6.3.9.1.
• Teste de Kolmogorov-Smirnov para duas amostras independentes, Seção 6.3.11.1.

Exemplo 6.72 Pode-se resolver o Exemplo 6.55 através do teste de Kruskal-Wallis.

# dados
x <- c(8,10,9,10,9, 7,8,5,8,5, 4,8,7,5,7)
g <- as.factor(rep(1:3, each = 5))
(k <- length(unique(g))) # número de grupos

## [1] 3

boxplot(x ~ g)

# validando suposição S4 via teste K-S para duas amostras indep.
ks.test(x[1:5], x[6:10])

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x[1:5] and x[6:10]
## D = 0.8, p-value = 0.04762
## alternative hypothesis: two-sided

ks.test(x[1:5], x[11:15])

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x[1:5] and x[11:15]
## D = 0.8, p-value = 0.07937
## alternative hypothesis: two-sided

ks.test(x[6:10], x[11:15])

## 
##  Exact two-sample Kolmogorov-Smirnov test
## 
## data:  x[6:10] and x[11:15]
## D = 0.2, p-value = 1
## alternative hypothesis: two-sided

# aplicando o teste de Kruskal-Wallis
kruskal.test(x,g)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  x and g
## Kruskal-Wallis chi-squared = 8.7474, df = 2, p-value = 0.0126

# comparando com a ANOVA
summary(aov(x ~ g))

##             Df Sum Sq Mean Sq F value  Pr(>F)   
## g            2  26.53   13.27   6.982 0.00974 **
## Residuals   12  22.80    1.90                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Teste post hoc de Dunn
FSA::dunnTest(x ~ g, method = 'bh')

##   Comparison         Z     P.unadj      P.adj
## 1      1 - 2 2.3402675 0.019269934 0.02890490
## 2      1 - 3 2.7363127 0.006213195 0.01863958
## 3      2 - 3 0.3960453 0.692071636 0.69207164

Exemplo 6.73 Em Python.

import numpy as np
import pandas as pd
from scipy.stats import ks_2samp, kruskal
import statsmodels.formula.api as smf
from scikit_posthocs import posthoc_dunn
import matplotlib.pyplot as plt

# Dados
x = np.array([8, 10, 9, 10, 9, 7, 8, 5, 8, 5, 4, 8, 7, 5, 7])
g = np.array([1] * 5 + [2] * 5 + [3] * 5)

# Convertendo para DataFrame do pandas
df = pd.DataFrame({'x': x, 'g': g})

# Validando suposição S4 (distribuições semelhantes) via teste K-S
statistic, p_value = ks_2samp(x[0:5], x[5:10])
print(f"Teste KS para grupo 1 e grupo 2: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

statistic, p_value = ks_2samp(x[0:5], x[10:15])
print(f"Teste KS para grupo 1 e grupo 3: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

statistic, p_value = ks_2samp(x[5:10], x[10:15])
print(f"Teste KS para grupo 2 e grupo 3: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# Teste de Kruskal-Wallis
statistic, p_value = kruskal(*[df['x'][df['g'] == group] for group in df['g'].unique()])
print(f"\nTeste de Kruskal-Wallis: estatística = {statistic:.4f}, p-valor = {p_value:.4f}")

# ANOVA (para comparação)
model = smf.ols('x ~ C(g)', data=df).fit()
anova_table = model.summary().tables[0]
print("\nTabela ANOVA (statsmodels):")
print(anova_table)

# Teste post hoc de Dunn
dunn_result = posthoc_dunn(df, val_col='x', group_col='g', 
                           p_adjust='bonferroni')
print("\nTeste Post-Hoc de Dunn:")
print(dunn_result)

Exercício 6.20 Refaça o exercício 6.17 aplicando o teste de Kruskal-Wallis.

References

Bartlett, Maurice Stevenson. 1937. “Properties of Sufficiency and Statistical Tests.” Proceedings of the Royal Society of London. Series A-Mathematical and Physical Sciences 160 (901): 268–82. https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.1937.0109.

Beasley, T Mark, and Randall E Schumacker. 1995. “Multiple Regression Approach to Analyzing Contingency Tables: Post Hoc and Planned Comparison Procedures.” The Journal of Experimental Education 64 (1): 79–93.

Brown, Morton B, and Alan B Forsythe. 1974. “Robust Tests for the Equality of Variances.” Journal of the American Statistical Association 69 (346): 364–67. https://dacemirror.sci-hub.gg/journal-article/e0e938059c61434c6e1997484213cd57/brown1974.pdf.

Conover, William J, Mark E Johnson, and Myrle M Johnson. 1981. “A Comparative Study of Tests for Homogeneity of Variances, with Applications to the Outer Continental Shelf Bidding Data.” Technometrics 23 (4): 351–61. http://staff.ustc.edu.cn/~zwp/teach/nonpar/Test%20for%20homogeneity%20of%20variances.pdf.

DeGroot, Morris H, and Mark J Schervish. 2012. Probability and Statistics. Pearson Education.

Ebbert, Daniel. 2019. Chisq.posthoc.test: A Post Hoc Analysis for Pearson’s Chi-Squared Test for Count Data. https://CRAN.R-project.org/package=chisq.posthoc.test.

———. 1936. “Has Mendel’s Work Been Rediscovered?” Annals of Science 1 (2): 115–37. https://www.tandfonline.com/doi/abs/10.1080/00033793600200111.

———. 1925. Statistical Methods for Research Workers. Oliver; Boyd, Edinburgh; London.

Fligner, Michael A, and Timothy J Killeen. 1976. “Distribution-Free Two-Sample Tests for Scale.” Journal of the American Statistical Association 71 (353): 210–13. https://www.tandfonline.com/doi/abs/10.1080/01621459.1976.10481517.

Hartl, Daniel L, and Daniel J Fairbanks. 2007. “Mud Sticks: On the Alleged Falsification of Mendel’s Data.” Genetics 175 (3): 975–79. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1840063/.

Hartley, Herman O. 1950. “The Maximum f-Ratio as a Short-Cut Test for Heterogeneity of Variance.” Biometrika 37 (3/4): 308–12. https://www.jstor.org/stable/2332383.

Ivanović, Blagoje, Bojana Milošević, and Marko Obradović. 2023. Symmetry: Testing for Symmetry of Data and Model Residuals. https://CRAN.R-project.org/package=symmetry.

Levene, H. 1960. “Robust Tests for Equality of Variances.” Contributions to Probability; Statistics: Essays in Honor of Harold Hotelling. https://archive.org/details/contributionstop0000unse_d2c5.

Milošević, Bojana, and Marko Obradović. 2018. “Comparison of Efficiencies of Some Symmetry Tests Around an Unknown Centre.” Statistics 53 (1): 43–57. https://doi.org/10.1080/02331888.2018.1526938.

Novitski, E. 2004. “On Fisher’s Criticism of Mendel’s Results with the Garden Pea.” Genetics 166 (3): 1133–36. https://www.genetics.org/content/genetics/166/3/1133.full.pdf.

Pereira, Carlos Alberto de Braganca, and Sergio Wechsler. 1993. “On the Concept of P-Value.” Brazilian Journal of Probability and Statistics, 159–77. https://www.jstor.org/stable/pdf/43600839.pdf.

Sheskin, David J. 2011. Handbook of Parametric and Nonparametric Statistical Procedures, 5th Ed. Chapman & Hall/CRC, Boca Raton, FL.

Welch, Bernard L. 1938. “The Significance of the Difference Between Two Means When the Population Variances Are Unequal.” Biometrika 29 (3/4): 350–62. https://www.jstor.org/stable/2332010.

---

43. “The value for which P=.05, or 1 in 20, is 1.96 or nearly 2; it is c to take this point as a limit in judging whether a deviation is to be considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant.” Ronald Aylmer Fisher na primeira edição do seu livro Statistical Methods For Research Workers, de 1925.↩︎

44. Ainda que (Ronald A. Fisher 1936) tenha posto dúvida sobre o trabalho de Mendel ao criar a noção do paradoxo mendeliano, ou ‘bom demais para ser verdade’. Tal consideração tem bases eugenistas e incondicionalistas, calcada sob uma ótica pouco embasada assumida por Ronald Fisher e seus mentores, Karl Pearson e Francis Galton, e refutada por acadêmicos como (Novitski 2004) e (Hartl and Fairbanks 2007).↩︎

45. A análise post hoc é aplicada quando uma hipótese de múltiplas igualdades é rejeitada, admitindo-se que ‘há pelo menos dois grupos distintos’. Neste caso, fica a pergunta: quais grupos são distintos e em que grau? A terminologia é baseada na expressão latina que significa ‘depois disto’.↩︎