2.3 Medidas de Localização

As medidas de localização ou posição estão associadas aos parâmetros de localização

2.3.1 Mínimo e Máximo

O mínimo de uma distribuição é o menor valor observado desta distribuição; de forma análoga, o máximo é o maior valor. São estatísticas de ordem, mais especificamente os extremos de um conjunto de dados ordenado (rol). Para uma distribuição de \(n\) elementos são denotadas por \(\min X = x_{(1)}\) e \(\max X = x_{(n)}\).

Apesar da simplicidade destas medidas, existem considerações teóricas sofisticadas a seu respeito. Para maiores detalhes, vide (S. Kotz and Nadarajah 2000).

Exemplo 2.35 (Mínimo e máximo) Suponha novamente as \(n=100\) observações da variável \(Y\): ‘altura de mulheres atendidas em um certo hospital público de Porto Alegre em 2020’, apresentadas no Exemplo 2.25. O mínimo e o máximo são denotados, respectivamente, por \(\min Y = y_{(1)} = 1.51\) e \(\max Y = y_{(100)} = 1.74\).

h <- read.csv('https://filipezabala.com/data/hospital.csv')
min(h$height)     # Mínimo

## [1] 1.51

max(h$height)     # Máximo

## [1] 1.74

range(h$height)   # A função 'range' fornece o mínimo e o máximo

## [1] 1.51 1.74

Exemplo 2.36 Em Python.

import pandas as pd

# Carrega o conjunto de dados
h = pd.read_csv('https://filipezabala.com/data/hospital.csv')

# Mínimo
print(min(h['height']))  # Output: 1.47

# Máximo
print(max(h['height']))  # Output: 1.83

# A função np.ptp() fornece o mínimo e o máximo
print(np.ptp(h['height']))  # Output: 0.36

2.3.2 Total

[Total ou somatório(https://en.wikipedia.org/wiki/Summation) (veja Seção 1.8) é a soma de todos os valores de uma variável. É expresso pelas equações (2.11) e (2.12).

\[\begin{equation} \tau = \sum_{i=1}^N x_i \tag{2.11} \end{equation}\]

\[\begin{equation} \hat{\tau} = N \bar{x}_{n}, \tag{2.12} \end{equation}\]

onde \(\bar{x}_{n}\) é a média amostral, conforme Equação (2.14).

Exemplo 2.37 (Total) Suponha novamente os dados do Exemplo 2.39. Se alguém precisar de uma lixeira 60 vezes na capital gaúcha, estima-se que o número total de passos a serem caminhados é de \[\hat{\tau} = \frac{60}{6} \times 930 = 60 \times 155 = 9300\]

N <- 60                         # Tamanho do universo/população
x <- c(186,402,191,20,7,124)    # Dados brutos
N*mean(x)                       # Equação (2.11)

## [1] 9300

Exemplo 2.38 Em Python.

import numpy as np

# Tamanho do universo/população
N = 60

# Dados brutos
x = np.array([186, 402, 191, 20, 7, 124])

# Equação (2.11)
total = N * np.mean(x)
print(total)  # Output: 18900.0

2.3.3 Média (Aritmética)

A média (aritmética) é uma das medidas mais importantes da Estatística devido às suas propriedades e relativa facilidade de cálculo. A média da variável \(X\) é simbolizada genericamente por \(\mu\) quando refere-se à média universal, e por \(\bar{x}\) quando refere-se à média amostral. Pode-se utilizar a notação \(\bar{x}_{n}\) para indicar o tamanho da amostra. Suas expressões no universo e na amostra são dadas respectivamente pelas equações (2.13) e (2.14). Por distribuir a soma dos valores da distribuição pelo número de observações, a média é uma medida que indica centro de massa. \[\begin{equation} \mu = \frac{\sum_{i=1}^N x_i}{N} \tag{2.13} \end{equation}\]

\[\begin{equation} \bar{x}_{n} = \frac{\sum_{i=1}^n x_i}{n} \tag{2.14} \end{equation}\]

Exemplo 2.39 (Média aritmética) Suponha novamente os dados do Exemplo 1.13. O número médio de passos até a lixeira mais próxima foi de \[\bar{x}_6 = \frac {\sum_{i=1}^6 x_i}{6} = \frac {186+402+191+20+7+124}{6} = \frac{930}{6} = 155.\]

x <- c(186,402,191,20,7,124)      # Dados brutos
mean(x)                           # Eq. (2.8) e (2.9). Veja ?mean

## [1] 155

Exemplo 2.40 Em Python.

import numpy as np

# Dados brutos
x = np.array([186, 402, 191, 20, 7, 124])

# Calculando a média
media = np.mean(x)
print(media)  # Output: 155.0

2.3.3.1 Lei dos grandes números

A lei dos grandes números (LGN) foi proposta por (Poisson 1837, 7), e “[c]onsiste no fato de que, se observarmos um número considerável de acontecimentos da mesma natureza, (…) encontraremos, entre esses números, relações aproximadamente constantes”¹⁰¹¹. Atualmente fala-se nas leis dos grandes números, visto que há diferentes resultados envolvendo a proposta original. Essencialmente a LGN indica que a média amostral \(\bar{x}_n\) converge para a média universal \(\mu\) quando \(n \rightarrow \infty\). (Samuel Kotz et al. 2005, 3979) definem três variantes, das quais listam-se as duas mais conhecidas. Para detalhes da lei dos grandes números de Erdös-Rényi, veja (Erdös and Rényi 1970).

Lei (forte) dos grandes números de Borel
Se \(X_1,\ldots,X_n\) é uma sequência de variáveis aleatórias condicionalmente independentes, identicamente distribuídas \(\mathcal{Ber}(\theta)\), i.e., \(Pr(X_i = 1)=\theta\) e \(Pr(X_i = 0)=1-\theta\) para todo \(i = 1,\ldots,n\), então \(\bar{x}_n \rightarrow \theta\) quase certamente quando \(n \rightarrow \infty\), i.e., \[\begin{equation} Pr\left[ \lim_{n \rightarrow \infty} \frac{\sum_{i=1}^n X_i}{n} = \theta \right] = 1 \tag{2.15} \end{equation}\]

Lei (fraca) dos grandes números de Chebyshev
Se \(X_1,\ldots,X_n\) é uma sequência de variáveis aleatórias condicionalmente independentes, tal que \(E(X_i)=m_i\) e \(Var(X_i)=\sigma_i^2\), \(i = 1,\ldots,n\), e \(\sigma_i^2 \le c < \infty\), então para qualquer \(\varepsilon > 0\), \(\bar{x}_n \rightarrow \mu\) em probabilidade quando \(n \rightarrow \infty\), i.e., \[\begin{equation} \lim_{n \rightarrow \infty} Pr\left[ \left| \frac{\sum_{i=1}^n X_i}{n} - \frac{\sum_{i=1}^n m_i}{n} \right| < \varepsilon \right] = 1 \tag{2.16} \end{equation}\]

Exemplo 2.41 Suponha \(M=20\,000\) lançamentos de um dado equilibrado. Pela Eq. (3.41) sabe-se que o valor esperado neste caso é \(E(X)=\frac{1+2+3+4+5+6}{6}=3.5\).

M <- 20000
theta <- 1/6
media <- vector(length = M)
sim <- base::sample(1:6, M, replace = TRUE, prob = rep(theta,6))
for(i in 1:M){
  set.seed(i+314); media[i] <- mean(sim[1:i])
}
plot(media, type = 'l', las = 1,
     main = '20 mil lançamentos de um dado equilibrado')
EX <- mean(1:6)
abline(h = EX, col = 'red')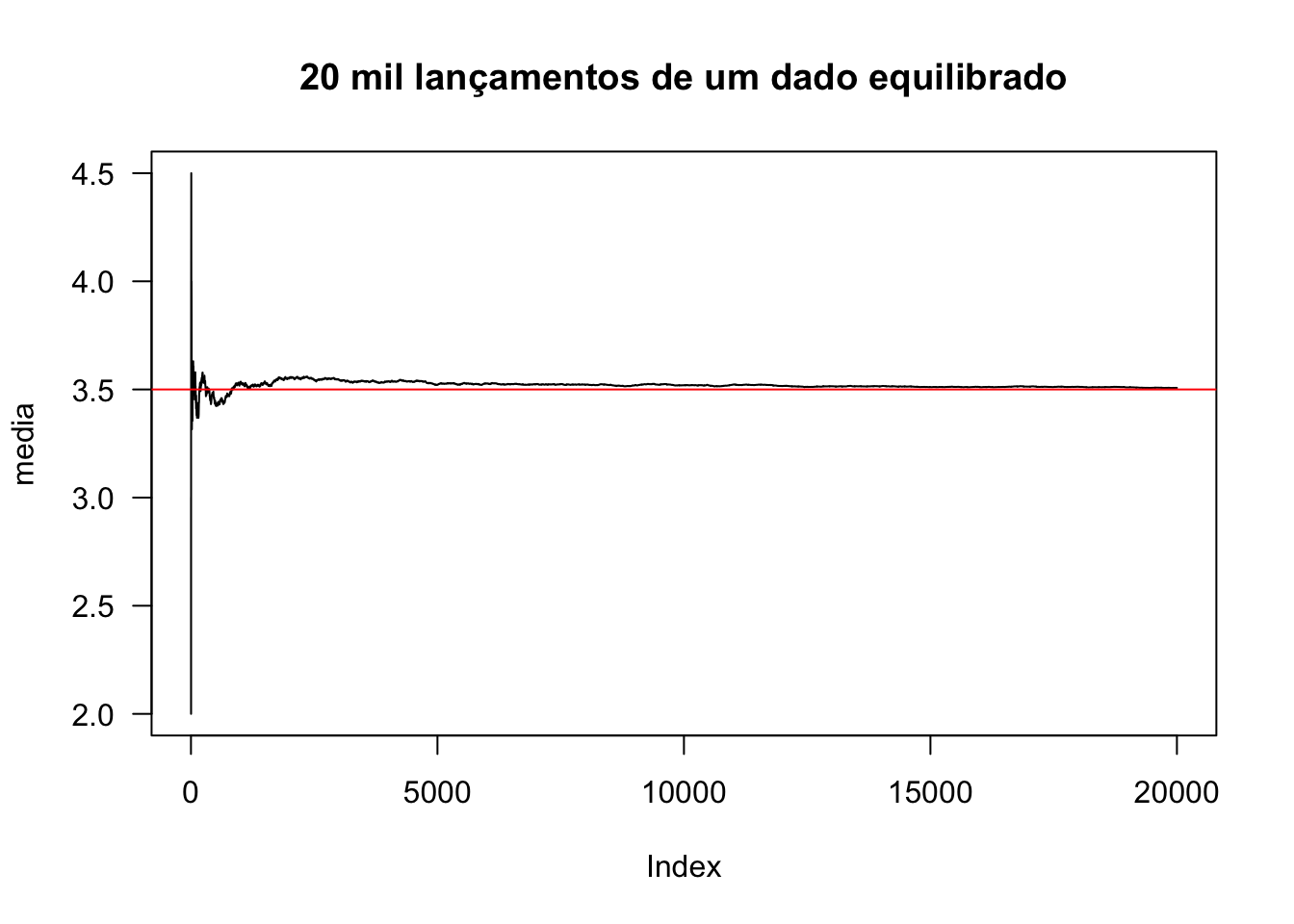

Exemplo 2.42 Em Python.

import numpy as np
import matplotlib.pyplot as plt

# Parâmetros
M = 20000
theta = 1/6

# Simulação
media = np.zeros(M)
sim = np.random.choice(np.arange(1, 7), size=M, 
                       replace=True, p=np.repeat(theta, 6))

for i in range(1, M + 1):
  np.random.seed(i + 314)
  media[i - 1] = np.mean(sim[:i])

# Plot
plt.plot(media, linestyle='-', color='blue')
plt.xlabel('Número de lançamentos')
plt.ylabel('Média acumulada')
plt.title('20 mil lançamentos de um dado equilibrado')

# Valor esperado
EX = np.mean(np.arange(1, 7))
plt.axhline(y=EX, color='red', linestyle='--')

plt.show()

Exercício 2.8 Considere o Exemplo 2.41.
a. Implemente para dois dados.
b. Varie o número de simulações \(M\).

2.3.3.2 Média (Aritmética) Ponderada

A média (aritmética) ponderada permite atribuir pesos distintos para as observações.

\[\begin{equation} \bar{x}_{n} = \frac{\sum_{i=1}^n w_i x_i}{\sum_{i=1}^n w_i} \tag{2.17} \end{equation}\]

Exemplo 2.43 (Água do chimarrão) Média ponderada é como colocar água quente e fria para regular a temperatura do mate. Suponha 1 litro de água em uma garrafa térmica, onde coloque-se \(w_1=850\)mL (85%) de água a \(x_1=96\,^{\circ}{\rm C}\) e \(w_2=150\)mL (15%) de água a \(x_2=30\,^{\circ}{\rm C}\). Desconsiderando variações externas, essa mistura deve ficar em \[ W = \frac {850mL \times 96\,^{\circ}{\rm C} + 150mL \times 30\,^{\circ}{\rm C}}{850mL + 150mL} = 0.85 \times 96\,^{\circ}{\rm C}+0.15 \times 30\,^{\circ}{\rm C} = 86.1\,^{\circ}{\rm C}.\]

weighted.mean(c(96,30), c(850,150)) # Facilita uma barbaridade

## [1] 86.1

Exemplo 2.44 Em Python.

import numpy as np

# Dados
valores = np.array([96, 30])
pesos = np.array([850, 150])

# Média ponderada
media_ponderada = np.average(valores, weights=pesos)
print(media_ponderada)  # Output: 85.2

2.3.3.3 Média aparada

Aparar um vetor de dados significa retirar uma fração (usualmente entre 0 e 0.5) de cada um dos extremos do vetor ordenado. A média aparada consiste em calcular a média aritmética do vetor aparado. Uma definição formal pode ser encontrada em (Yuen 1974, 166).

x <- c(2:99,1000,10000) # Vetor original, com valores extremos
mean(x)                 # Média aritmética

## [1] 159.49

mean(x, trim = 0.01)    # Retira 1% dos valores extremos

## [1] 60.68367347

mean(sort(x[2:99]))     # mean(x, trim = 0.01) 

## [1] 60.68367347

mean(x, trim = 0.25)    # Média interquartílica

## [1] 51.5

mean(sort(x[26:75]))    # mean(x, trim = 0.25)

## [1] 51.5

Exemplo 2.45 Em Python.

import numpy as np

# Vetor original, contendo valores extremos
x = np.array(list(range(2, 100)) + [1000, 10000])

# Média aritmética
print(np.mean(x))  # Output: 154.5

# Retira 1% dos valores extremos
print(np.mean(x, trim=0.01)) # Output: 50.495

# Equivalente a mean(x, trim = 0.01)
x_sorted = np.sort(x)
n = len(x)
trim_index = int(0.01 * n)
print(np.mean(x_sorted[trim_index:n - trim_index])) # Output: 50.495

# Média interquartílica: retira 25% dos valores extremos
print(np.mean(x, trim=0.25)) # Output: 50.5

# Equivalente a mean(x, trim = 0.25)
x_sorted = np.sort(x)
n = len(x)
trim_index = int(0.25 * n)
print(np.mean(x_sorted[trim_index:n - trim_index])) # Output: 50.5

2.3.3.4 Média Winsorizada

Winsorizar um vetor (ordenado) significa substituir uma certa proporção de valores extremos por valores menos extremos. Assim, os valores substitutos são os valores retidos mais extremos. Uma definição formal pode ser encontrada em (Yuen 1974, 166).

x <- c(2:99,1000,10000) # Vetor original, contendo valores extremos
xw <- DescTools::Winsorize(x, val=quantile(x, probs=c(0.01, 0.99)))
mean(x)

## [1] 159.49

mean(xw)

## [1] 70.3999

Exemplo 2.46 Em Python.

import numpy as np
from scipy.stats.mstats import winsorize

# Vetor original, contendo valores extremos
x = np.array(list(range(2, 100)) + [1000, 10000])

# Calculando os quantis para winsorização
lower_limit = np.quantile(x, 0.01)
upper_limit = np.quantile(x, 0.99)

# Aplicando a winsorização
xw = winsorize(x, limits=(0.01, 0.01))

# Média original
print(np.mean(x))  # Output: 154.5

# Média winsorizada
print(np.mean(xw))  # Output: 50.99

2.3.4 Média Quadrática

A média quadrática é a média dos valores ao quadrado, utilizada no cálculo das variâncias. É também conhecida como segundo momento (não centrado). \[\begin{equation} MS = \frac{\sum_{i=1}^n x_{i}^{2}}{n}. \tag{2.18} \end{equation}\]

A raiz da média quadrática, raiz do valor quadrático médio ou valor eficaz é a raiz quadrada da média quadrática. \[\begin{equation} RMS=\sqrt{MS}. \tag{2.19} \end{equation}\]

Exemplo 2.47 (MS e RMS) A média quadrática dos valores 186, 402, 191, 20, 7 e 124 é \[Q = \frac{\sum_{i=1}^6 x_{i}^{2}}{6} = \frac{186^2+402^2+191^2+20^2+7^2+124^2}{6} = \frac{248506}{6} = 41417.\bar{6}.\] A raiz da média quadrática é \[RMS = \sqrt{41417.\bar{6}} \approx 203.5133.\]

x <- c(186,402,191,20,7,124) # Dados brutos
(ms <- mean(x^2))           # Eq. (2.18), compare com mean(x)^2

## [1] 41417.66667

sqrt(ms)                    # Eq. (2.19), raiz da média quadrática

## [1] 203.5133083

Exemplo 2.48 Em Python.

import numpy as np

# Dados brutos
x = np.array([186, 402, 191, 20, 7, 124])

# Eq. (2.12)
ms = np.mean(x**2)
print(ms)  # Output: 36928.333333333336

# Comparando com mean(x)^2
print(np.mean(x)**2)  # Output: 24025.0

# Eq. (2.13)
rms = np.sqrt(ms)
print(rms)  # Output: 192.16745259789917

2.3.5 Média Harmônica

A média harmônica é utilizada para calcular médias de taxas. É definida por \[\begin{equation} H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} = \frac{n}{\sum_{i=1}^n \frac{1}{x_i}}. \tag{2.20} \end{equation}\]

Exemplo 2.49 (Média harmônica) Suponha que um veículo viajou uma certa distância a 60 km/h e a mesma distância novamente a 90 km/h. Sua velocidade média pode ser calculada pela média harmônica \[H = \frac{2}{\frac{1}{60} + \frac{1}{90}} = 72 km/h,\] i.e., se o veículo percorresse toda a distância a 72 km/h, faria o trajeto no mesmo tempo.

2/((1/60)+(1/90))       # Pela Equação (2.20)

## [1] 72

1/mean(1/c(60,90))      # Alternativa

## [1] 72

Exemplo 2.50 Em Python.

import numpy as np

# Pela Equação (2.20)
resultado1 = 2 / ((1/60) + (1/90))
print(resultado1)  # Output: 72.0

# Alternativa
resultado2 = 1 / np.mean(1 / np.array([60, 90]))
print(resultado2)  # Output: 72.0

2.3.6 Média Geométrica

Média geométrica é uma entre as três médias pitagóricas, utilizada para representação de conjuntos que se comportam como progressão geométrica. Raul Rodrigues de Oliveira em Brasil Escola UOL

A média geométrica é utilizada para calcular médias de índices e acelerações, bem como em casos em que as medidas possuam magnitudes numéricas distintas. É definida por \[\begin{equation} G = \sqrt[n]{\Pi_{i=1}^n x_i}. \tag{2.21} \end{equation}\]

Exemplo 2.51 (Média geométrica) Sejam os índices de preço \(L_{2004,2008}^{P} = 139.58\%\) e \(P_{2004,2008}^{P} = 97.22\%\). Sua média geométrica é conhecida como índice (ideal) de Fisher, dada por \[G = \sqrt{1.3958 \times 0.9722} \approx 116.49\%.\]

sqrt(1.3958*.9722)

## [1] 1.164902039

Exemplo 2.52 Em Python.

import math

# Calculando a raiz quadrada
resultado = math.sqrt(1.3958 * 0.9722)
print(resultado)  # Output: 1.1650062234417873

2.3.7 Relação entre médias

Seja \(H\) a média harmônica (Eq. (2.20)), \(G\) a média geométrica (Eq. (2.21)), \(A \equiv \mu\) a média aritmética (Eq. (2.13)) e \(Q \equiv MS\) a média quadrática (Eq. (2.18)). Se aplicadas a valores positivos, então \[H \le G \le A \le Q.\]

2.3.8 Moda

Moda(s) é (são) o(s) valor(es) mais frequente(s) de uma distribuição. Quando os dados estão agrupados deve-se indicar a classe modal, i.e., a classe de maior frequência. O esforço computacional para calcular a moda é realizar uma contagem.

• Amodal: sem moda
• Unimodal: uma moda
• Bimodal: duas modas
• Trimodal: três modas
• Polimodal: quatro ou mais modas

No R existem funções como pracma::Mode, mas ela só funciona bem no caso unimodal. Por isso a seguir está apresentada a função Modes, adaptada da sugestão de digEmAll nesta discussão do StackOverflow. Nos exemplos a seguir são comparadas as duas abordagens.

# Função Modes
Modes <- function(x){
  ux <- sort(unique(x))
  tab <- tabulate(match(x, ux))
  if(sum(diff(tab)^2) == 0){
    return('Amodal')
  } else{
    return(ux[tab == max(tab)]) 
  }
}

Exemplo 2.53 Em Python.

import numpy as np
from scipy import stats

def Modes(x):
  """
  Calcula a moda (ou modas) de um conjunto de dados.

  Args:
    x: Um array NumPy ou lista de valores.

  Returns:
    Um array NumPy contendo a(s) moda(s) do conjunto de dados.
    Se todos os valores têm a mesma frequência, retorna None.
  """
  ux = np.sort(np.unique(x))
  tab = np.bincount(np.searchsorted(ux, x))
  # Verifica se todos os valores têm a mesma frequência
  if np.all(tab == tab[0]):
    return None
  else:
    return ux[tab == np.max(tab)]

Exemplo 2.54 (Unimodal) A moda do conjunto de dados 4, 7, 1, 3, 3, 9 é \(Mo=3\), pois ele apresenta frequência 2 enquanto os demais valores têm frequência 1. Esta é uma distribuição unimodal.

dat <- c(4,7,1,3,3,9)
Modes(dat)

## [1] 3

pracma::Mode(dat)

## [1] 3

Exemplo 2.55 Em Python.

import numpy as np
from scipy import stats

dat = np.array([4, 7, 1, 3, 3, 9])

# Usando a função Modes()
print(Modes(dat))  # Output: [3]

# Usando scipy.stats.mode() (similar a pracma::Mode(dat))
moda, contagem = stats.mode(dat)
print(moda)  # Output: [3]

Exemplo 2.56 (Bimodal) As modas do conjunto de dados 4, 7, 1, 3, 3, 9, 7 são \(Mo'=3\) e \(Mo''=7\), pois ambos têm frequência 2 enquanto os demais valores têm frequência 1. A ordem de apresentação é indiferente. Esta é uma distribuição bimodal.

dat <- c(4,7,1,3,3,9,7)
Modes(dat)

## [1] 3 7

pracma::Mode(dat)

## [1] 3

Exemplo 2.57 Em Python.

import numpy as np
from scipy import stats

dat = np.array([4, 7, 1, 3, 3, 9, 7])

# Usando a função Modes()
print(Modes(dat))  # Output: [3 7]

# Usando scipy.stats.mode() (similar a pracma::Mode(dat))
moda, contagem = stats.mode(dat)
print(moda)  # Output: [3]

Exemplo 2.58 In Python.

import numpy as np
from scipy import stats

dat = np.array([4, 7, 1, 3, 3, 9, 7])

# Using the Modes() function
print(Modes(dat)) # Output: [3 7]

# Using scipy.stats.mode() (similar to pracma::Mode(dat))
moda, contagem = stats.mode(dat)
print(moda) # Output: [3]

Exemplo 2.59 (Amodal) O conjunto de dados 4, 7, 1, 3, 9 é dito amodal pois todos os valores têm frequência 1.

dat <- c(4,7,1,3,9)
Modes(dat)  # Se todo valor for moda, nenhum valor será moda

## [1] "Amodal"

pracma::Mode(dat)

## [1] 1

Exemplo 2.60 Em Python.

import numpy as np
from scipy import stats

dat = np.array([4, 7, 1, 3, 9])

# Usando a função Modes()
print(Modes(dat))  # Output: None

# Usando scipy.stats.mode() (similar a pracma::Mode(dat))
moda, contagem = stats.mode(dat)
print(moda)  # Output: [1]

Exemplo 2.61 (Moda para dados agrupados) No Exemplo 2.25 observa-se que \(f_{3}=41\) é a maior frequência. A classe modal é portanto a terceira, compreendida entre os valores 1.60 e 1.65.

2.3.9 Quantil

Quantil ou separatrizes são medidas que dividem um conjunto de dados ordenados em \(k\) partes (aproximadamente) iguais. O método básico consiste em obter um rol dos dados e encontrar (ainda que de forma aproximada) os valores que repartem a distribuição de acordo com o \(k\) desejado. O esforço computacional para calcular quaisquer separatrizes é, portanto, a ordenação dos dados. De forma geral, pode-se definir uma separatriz \(S\) conforme a Eq. (2.22), onde \(n\) indica o número de observações e \(p\) a proporção de observações ordenadas abaixo de \(S\). \[\begin{equation} S = x_{(p(1+n))} \tag{2.22} \end{equation}\]

A função stats::quantile() apresenta nove métodos para obtenção de quantis, portanto recomenda-se a documentação para maiores detalhes. Com ela pode-se facilmente obter os quantis desejados, bastando ajustar o argumento \(p\). Note que a função retorna os quantis expressos em percentis, onde \(0\%\) equivale ao mínimo e \(100\%\) ao máximo.

2.3.9.1 Mediana

A mediana é a medida que divide metade dos dados ordenados à sua esquerda e a outra metade à sua direita. Pode ser descrita como a estatística de \(\frac{1+n}{2}\)ésima ordem conforme Eq. (2.24). É a medida central em termos de ordenação, e sua posição é a média entre a primeira e última posições conforme Eq. (2.23). \[\begin{equation} Pos = \frac{1+n}{2} \tag{2.23} \end{equation}\]

\[\begin{equation} Md = x_{\left( \frac{1+n}{2} \right)} \tag{2.24} \end{equation}\]

Exemplo 2.62 (Mediana para \(n\) ímpar) Considere a sequência regular de \(0\) a \(100\). A posição da mediana é \(Pos = \frac{1+101}{2}=51\), portanto \(Md=x_{(51)}=50\).

x <- 0:100
sort(x)[51]

## [1] 50

median(x)

## [1] 50

quantile(x, 1/2)

## 50% 
##  50

Exemplo 2.63 Em Python.

import numpy as np

x = np.arange(0, 101)

# Ordenando x e pegando o 51º elemento
print(np.sort(x)[50])  # Output: 50

# Calculando a mediana
print(np.median(x))  # Output: 50.0

# Calculando o quantil 1/2 (equivalente à mediana)
print(np.quantile(x, 1/2))  # Output: 50.0

Exemplo 2.64 (Mediana para \(n\) par) Quando o número de observações é par, basta tomar a média dos dois valores centrais do rol. Considere o conjunto de dados \(15,-4,11,12,1,5\). A posição da mediana é \(Pos_{\frac{1}{2}} = \frac{1+6}{2}=3.5\), e o rol \(-4,1,5,11,12,15\). Portanto \(Md=x_{(3.5)}=\frac{x_{(3)}+x_{(4)}}{2}=\frac{5+11}{2}=8\).

x <- c(15,-4,11,12,1,5)
(n <- length(x))

## [1] 6

(pos <- (1+n)/2)

## [1] 3.5

sort(x)

## [1] -4  1  5 11 12 15

median(x)

## [1] 8

Exemplo 2.65 Em Python.

import numpy as np

x = np.array([15, -4, 11, 12, 1, 5])

# Calculando o tamanho do array
n = len(x)
print(n)  # Output: 6

# Calculando a posição da mediana
pos = (1 + n) / 2
print(pos)  # Output: 3.5

# Ordenando o array
x_sorted = np.sort(x)
print(x_sorted)  # Output: [-4  1  5 11 12 15]

# Calculando a mediana
print(np.median(x))  # Output: 8.0

2.3.9.2 Quartis

As posições do primeiro e terceiro quartis podem ser definidos respectivamente pelas Eq. (2.25) e (2.26). Este é o algoritmo \(\hat{Q}_6(p)\) conforme (Hyndman and Fan 1996), ou type=6 na função stats::quantile().

\[\begin{equation} Pos_{\frac{1}{4}} = \frac{1+n}{4} \tag{2.25} \end{equation}\]

\[\begin{equation} Pos_{\frac{3}{4}} = \frac{3(1+n)}{4} \tag{2.26} \end{equation}\]

O primeiro e terceiro quartis podem ser definidos respectivamente pelas Eq. (2.27) e (2.28).

\[\begin{equation} Q_1 = x_{\left( \frac{1+n}{4} \right)} \tag{2.27} \end{equation}\]

\[\begin{equation} Q_3 = x_{\left( \frac{3(1+n)}{4} \right)} \tag{2.28} \end{equation}\]

Exemplo 2.66 Considere novamente a sequência regular de 0 a 100. A posição do primeiro quartil é \(Pos_{\frac{1}{4}} = \frac{1+101}{4}=25.5\), e a do terceiro quartil \(Pos_{\frac{3}{4}} = \frac{3(1+101)}{4}=76.5\). Portanto \(Q_1=x_{(25.5)}=\frac{x_{(25)}+x_{(26)}}{2}=\frac{24+25}{2}=24.5\) e \(Q_3=x_{(76.5)}=\frac{x_{(76)}+x_{(77)}}{2}=\frac{75+76}{2}=75.5\).

x <- 0:100
sort(x)[25]

## [1] 24

sort(x)[26]

## [1] 25

sort(x)[76]

## [1] 75

sort(x)[77]

## [1] 76

quantile(x, c(1/4,3/4), type = 6)

##  25%  75% 
## 24.5 75.5

Exemplo 2.67 Em Python.

import numpy as np

x = np.arange(0, 101)

# Calculando os quartis
quartis = np.quantile(x, [1/4, 3/4])
print(quartis)  # Output: [25.  75.]

## [25. 75.]

Pode-se dividir um conjunto de dados em \(k\) setores, sendo os principais apresentados na tabela a seguir

\(k\)	\(p=\frac{1}{k},\ldots,\frac{k-1}{k}\)	Nome	Simbologia
2	1/2	Mediana	Md
3	1/3, 2/3	Tercil	\(T_1\), \(T_2\)
4	1/4, 2/4, 3/4	Quartil	\(Q_1\), \(Q_2\), \(Q_3\)
10	1/10, …, 9/10	Decil	\(D_1\), \(D_2\), \(\ldots\), \(D_9\)
100	1/100, …, 99/100	Percentil	\(P_1\), \(P_2\), \(\ldots\), \(P_{99}\)

Exemplo 2.68 Alguns quantis com o algoritmo \(\hat{Q}_7(p)\) conforme (Hyndman and Fan 1996), ou type=7 na função stats::quantile().

h <- read.csv('https://filipezabala.com/data/hospital.csv')
options(digits = 4) # Para melhorar a apresentação
quantile(h$height, probs = seq(0, 1, 1/2))  # Mediana

##    0%   50%  100% 
## 1.510 1.625 1.740

quantile(h$height, probs = seq(0, 1, 1/3))  # Tercis

##        0% 33.33333% 66.66667%      100% 
##      1.51      1.61      1.65      1.74

quantile(h$height, probs = seq(0, 1, 1/4))  # Quartis

##    0%   25%   50%   75%  100% 
## 1.510 1.598 1.625 1.650 1.740

quantile(h$height, probs = seq(0, 1, 1/10)) # Decis

##    0%   10%   20%   30%   40%   50%   60%   70%   80%   90%  100% 
## 1.510 1.569 1.590 1.600 1.616 1.625 1.640 1.650 1.660 1.680 1.740

Exemplo 2.69 Em Python.

import pandas as pd
import numpy as np

# Carrega o conjunto de dados
h = pd.read_csv('https://filipezabala.com/data/hospital.csv')

# Define a precisão de exibição para 4 dígitos
pd.set_option("display.precision", 4)

# Mediana
print(np.quantile(h['height'], q=1/2))  # Output: 1.65

# Tercis
print(np.quantile(h['height'], q=[0, 1/3, 2/3, 1]))

# Quartis
print(np.quantile(h['height'], q=[0, 1/4, 2/4, 3/4, 1]))

# Decis
print(np.quantile(h['height'], q=np.arange(0, 1.1, 0.1)))

Exercício 2.9 Interprete os quantis do Exemplo 2.68.

Exercício 2.10 Considere as separatrizes discutidas nesta seção.
a. Verifique que as separatrizes mediana (Md), segundo quartil (\(Q_2\)) são equivalentes.
b. Existem outras medidas equivalentes às do item a? Justifique.
c. Considere diferentes \(k\) daqueles apresentados e atribua um nome e uma simbologia.
d. Se existem \(k\) segmentos, quantas são as separatrizes?

Exercício 2.11 Utilizando a função stats::quantile() calcule as separatrizes discutidas nesta Seção com os dados da coluna children disponível em https://filipezabala.com/data/hospital.csv.

2.3.10 Resumo de 5 números

O resumo de 5 números foi sugerido por (Tukey 1977, 32). Engloba mínimo, máximo, mediana e hinges (dobra/dobradiça/articulação) inferior e superior. Por não haver tradução oficial no Glossário de Estatística da SPE/ABE iremos nos referir ao hinge inferior como a mediana entre o mínimo e a mediana de todo o conjunto. De forma análoga o hinge superior será considerado como a mediana entre a mediana de todo o conjunto e o máximo. Dependendo do algoritmo utilizado no cálculo dos quartis, os hinges podem diferir ligeiramente destas separatrizes.

Exemplo 2.70 Considere o conjunto de dados utilizado por (Tukey 1977, 33).

x <- c(-3.2,-1.7,-0.4,0.1,0.3,1.2,1.5,1.8,2.4,3.0,4.3,6.4,9.8)
fivenum(x)

## [1] -3.2  0.1  1.5  3.0  9.8

quantile(x, probs = seq(0,1,1/4))

##   0%  25%  50%  75% 100% 
## -3.2  0.1  1.5  3.0  9.8

Exemplo 2.71 Em Python.

import numpy as np

x = np.array([-3.2,-1.7,-0.4,0.1,0.3,1.2,1.5,1.8,2.4,3.0,4.3,6.4,9.8])

# Calculando o resumo de cinco números (Tukey's five number summary)
print(np.quantile(x, q=[0, 0.25, 0.5, 0.75, 1]))  

# Calculando os quartis
print(np.quantile(x, q=[0, 1/4, 2/4, 3/4, 1]))

References

Erdös, P, and A Rényi. 1970. “On a New Law of Large Numbers.” Analyse Math 23: 103–11. https://link.springer.com/article/10.1007/BF02795493.

Hyndman, Rob J, and Yanan Fan. 1996. “Sample Quantiles in Statistical Packages.” The American Statistician 50 (4): 361–65. https://d1wqtxts1xzle7.cloudfront.net/51448589/Sample_Quantiles_in_Statistical_Packages20170120-21949-1uaj3m0-libre.pdf?1484951274=&response-content-disposition=inline%3B+filename%3DSample_Quantiles_In_Statistical_Packages.pdf&Expires=1735588403&Signature=aMof~CkpTDuG2evlTMQdWfAEirK0crSxUOyOJD7Gu0hnvNlWoxor5xzN27UMPnfZzODyW3mZih4fKTfbxVNnV9GUfolcx8jQcRmfMBOAcIFx5c0G4Ad91hecAv~orHpjC1D-b8WPanW9cYsbzmhc9lqScfS0a-eqXUq2aRVdhPz3iL1uPUFCwKOQKFRuITvfMnxPKqUejlrbpgtKCaAp0O~UjL81MbvthPvIINbzm4DC9GkZaUKsHeXcaAEffZhvh~t3g8hCg1MOcsm37CfbsPFwOou8hUchYdqmJNgGujw~iq7dGqSZvE4Otf71uNPNMlyfx91ipR4w6UbTilPxGQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA.

Kotz, Samuel, Narayanaswamy Balakrishnan, Campbell B Read, and Brani Vidakovic. 2005. Encyclopedia of Statistical Sciences. John Wiley & Sons.

Kotz, S, and S Nadarajah. 2000. Extreme Value Distributions. World Scientific. https://books.google.com.br/books/about/Extreme_Value_Distributions.html?id=ZPW3CgAAQBAJ&redir_esc=y.

Poisson, Siméon-Denis. 1837. Recherches Sur La Probabilité Des Jugements En Matière Criminelle Et En Matière Civile: Précédées Des règles générales Du Calcul Des Probabilités. Bachelier. https://archive.org/details/bub_gb__8FAjzHfzHgC/mode/2up.

Tukey, John W. 1977. Exploratory Data Analysis. Addison-Wesley Publishing Company.

Yuen, Karen K. 1974. “The Two-Sample Trimmed t for Unequal Population Variances.” Biometrika 61 (1): 165–70. https://www.jstor.org/stable/2334299.

---

10. “Les choses do toutes natures sont soumises à une loi universelle qu’on peut appeler la loi des grands nombres. Elle consiste en ce que, si l’on observe des nombres très considérables d’événements d’une même nature, dépendants de causes constantes et de causes qui varient irrégulièrement, tantôt dans un sens, tantôt dans l’autre, c’est-à-dire sans que leur variation soit progressive dans aucun sens déterminé, on trouvera, entve ces nombres, des rapports à très peu près constants.” https://archive.org/details/recherchessurla02poisgoog/page/n29/mode/2up↩︎

11. “Coisas de todas as naturezas estão sujeitas a uma lei universal que pode ser chamada de lei dos grandes números. Consiste no fato de que, se observarmos um número considerável de acontecimentos da mesma natureza, dependentes de causas constantes e de causas que variam irregularmente, ora numa direcção, ora noutra, é - isto é, sem a sua sendo a variação progressiva em qualquer direção determinada, encontraremos, entre esses números, relações aproximadamente constantes.”↩︎