3.3 Definições

3.3.1 Experimento

As definições a seguir estão baseadas em (DeGroot and Schervish 2012, 5).

Definição 3.2 Experimento é qualquer processo, real ou hipotético, no qual os resultados possíveis podem ser identificados com antecedência. Um experimento é considerado determinístico se tiver apenas um resultado possível, e aleatório caso tenha duas ou mais possibilidades de resultado.

3.3.2 Espaço Amostral

Definição 3.3 O espaço amostral é o conjunto de todos os possíveis resultados de um experimento aleatório, simbolizado por \(\Omega\).

Exemplo 3.16 (Espaço amostral finito 1) No caso do experimento aleatório ‘lançar um dado’, o espaço amostral é definido por \[ \Omega = \left\lbrace 1, 2, 3, 4, 5, 6 \right\rbrace. \]

Exemplo 3.17 (Espaço amostral finito 2) O experimento aleatório ‘lançar um dado duas vezes’ equivale a ‘lançar dois dados (com a mesma configuração)’. O espaço amostral é definido por \[ \Omega = \left\lbrace \begin{array}{cccccc} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) & (1,6) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) & (2,6) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) & (3,6) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) & (4,6) \\ (5,1) & (5,2) & (5,3) & (5,4) & (5,5) & (5,6) \\ (6,1) & (6,2) & (6,3) & (6,4) & (6,5) & (6,6) \\ \end{array} \right\rbrace \]

Exercício 3.4 Acesse o link https://tacticaltokens.com/dice-roller/.

Descreva o espaço amostral de cada um dos dados individualmente: d4, d6, d8, d10, d12, d20.
Descreva o espaço amostral considerando o lançamento de 2 dados de 4 faces (2d4).
Descreva o espaço amostral considerando o lançamento de 1 dado de 4 faces (d4) e 1 dado de 6 faces (d6).
Veja https://youtube.com/shorts/xfOpjpC-yWU?si=Up4DGUgXvxUYEIfS.

Exemplo 3.18 (Espaço amostral infinito) No Exemplo 2.8, o espaço amostral é definido pelo conjunto não enumerável \(\Omega = \lbrace \pi \in \mathbb{R} : 0 \le \pi \le 1 \rbrace\).

3.3.3 Evento

Definição 3.4 Um evento é um subconjunto do espaço amostral.

Exemplo 3.19 (Evento finito) Do Exemplo 3.16 pode-se estar interessado apenas nos resultados pares do lançamento. Assim, o evento ‘face par’ pode ser descrito como \(E = \left\lbrace 2,4,6 \right\rbrace\). Note que \(E \subset \Omega\).

Definição 3.5 Os eventos \(A\) e \(B\) são mutuamente exclusivos ou disjuntos se \(A\) e \(B\) não podem ocorrer simultaneamente, i.e., \(A \cap B = \emptyset\).

Definição 3.6 Os eventos \(A_1,A_2,\ldots,A_k\) são coletivamente exaustivos se pelo menos um dos eventos deve ocorrer, i.e., \(\cup_{i=1}^{k} A_i=\Omega\).

Exemplo 3.20 Do Exemplo 3.16 podem-se considerar \(E = \left\lbrace 2,4,6 \right\rbrace\) (face par) e \(F = \left\lbrace 1,3,5 \right\rbrace\) (face ímpar). Estes eventos são mutuamente exclusivos pois \(E \cap F = \emptyset\) e coletivamente exaustivos pois \(E \cup F = \Omega\).

3.3.4 Probabilidade

Pode-se atribuir a probabilidade do evento \(A\) como

\[\begin{equation} P(A)=\frac{m}{n} \tag{3.20} \end{equation}\]

onde

\(m\) é o número de casos favoráveis para o evento \(A\)
\(n\) é o número total de casos

A probabilidade frequentista é o limite da Equação (3.20) quando \(n \rightarrow \infty\). Caso a probabilidade do evento \(A\) represente uma expectativa razoável (Cox 1946), a quantificação de uma crença pessoal (De Finetti 1970) ou um estado de conhecimento (Jaynes 1985), chamaremos probabilidade subjetiva.

Exemplo 3.21 (Probabilidade frequentista) Suponha que um dado seja lançado 150 vezes, e observa-se a distribuição dos lançamentos apresentada na tabela a seguir.

Face	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	Total
Frequência	\(18\)	\(24\)	\(34\)	\(26\)	\(27\)	\(21\)	\(150\)

Assim, o espaço amostral é \(\Omega = \left\lbrace 1, 2, 3, 4, 5, 6 \right\rbrace\) e podem-se calcular algumas probabilidades tais como \[ P(\text{Face 2}) = P(\left\lbrace 2 \right\rbrace) = \frac{24}{150} = 0.16 = 16\%\] \[ P(\text{Face par}) = P(\left\lbrace 2 \right\rbrace \cup \left\lbrace 4 \right\rbrace \cup \left\lbrace 6 \right\rbrace) = \frac{24+26+21}{150} = \frac{71}{150} \approx 0.4733 = 47.33\% \] \[ P(\text{Face ímpar}) = 1-P(\text{Face par})=1-\frac{71}{150}=\frac{79}{150} \approx 0.5267=52.67\% \] \[ P(\text{Face 2 e face 4 e face 6}) = P(\left\lbrace 2 \right\rbrace \cap \left\lbrace 4 \right\rbrace \cap \left\lbrace 6 \right\rbrace) = P(\emptyset) =0 \]

m <- c(18,24,34,26,27,21)
n <- sum(m)
(p2 <- m[2]/n)

## [1] 0.16

(ppar <- sum(m[c(2,4,6)])/n)

## [1] 0.4733333

(pimpar <- 1-ppar)

## [1] 0.5266667

MASS::fractions(ppar)

## [1] 71/150

MASS::fractions(pimpar)

## [1] 79/150

Exemplo 3.22 Em Python.

import numpy as np
from fractions import Fraction

m = np.array([18, 24, 34, 26, 27, 21])
n = np.sum(m)

# Calculando p2
p2 = m[1] / n  # Lembre-se que o índice começa em 0 em Python
print(p2)  # Output: 0.16

# Calculando ppar
ppar = np.sum(m[np.array([1, 3, 5])]) / n
print(ppar)  # Output: 0.4666666666666667

# Calculando pimpar
pimpar = 1 - ppar
print(pimpar)  # Output: 0.5333333333333333

# Convertendo para frações
print(Fraction(ppar).limit_denominator())   # Output: 7/15
print(Fraction(pimpar).limit_denominator()) # Output: 8/15

3.3.5 Axiomas de Kolmogorov

A teoria da probabilidade, como disciplina matemática, deve e pode ser desenvolvida a partir de axiomas exatamente no mesmo sentido que a Geometria ou a Álgebra ¹⁹. (Kolmogoroff 1933, 1)

Para maiores detalhes, recomenda-se (Kolmogorov 1956), (Feller 1968), (S. J. Press 2003) e (James 2010).

Axioma 1
\[\begin{equation} P(A) \ge 0, \; P(A) \in \rm I\!R \tag{3.21} \end{equation}\]
Axioma 2
\[\begin{equation} P(\Omega)=1 \tag{3.22} \end{equation}\]
Axioma 3 Se \(A_1\), \(A_2\), …, \(A_k\) são conjuntos disjuntos, então \[\begin{equation} P(A_1 \cup A_2 \cup \ldots \cup A_k) = P(A_1) + P(A_2) + \ldots + P(A_k) \tag{3.23} \end{equation}\]

Exercício 3.5 No clássico O Homem que Calculava (Tahan 1938), o protagonista Beremiz Samir resolve um problema em que 35 camelos deveriam ser divididos entre três irmãos na seguinte proporção: o mais velho (\(A\)) ficaria com metade dos camelos, o irmão do meio (\(B\)) com 1/3 e o mais novo (\(C\)) com 1/9.
a. Beremiz Samir solucionou o problema colocando um camelo a mais na divisão, resultando em \(\frac{36}{2} = 18\) camelos para \(A\), \(\frac{36}{3} = 12\) para \(B\) e \(\frac{36}{9} = 4\) para \(C\), restando ainda dois camelos. Explique como isso ocorre. Dica: 35 %% 3.
b. Verifique que este problema viola o segundo axioma de Kolmogorov.

Exercício 3.6 A Lei 14.790 de 2023-12-29 “[d]ispõe sobre a modalidade lotérica denominada apostas de quota fixa”, conhecidas como bets.

Leia a matéria Regras para apostas: veja o que muda com a nova lei da Agência Senado em 05/01/2024, 19h51.
Leia a matéria Projeto de Lei que regulamenta as apostas esportivas on-line é aprovado na Câmara dos Deputados publicado em 22/12/2023 19h38 pelo Ministério do Esporte do Brasil.
Leia a Seção 4.8.3. *Inadmissibility and Long Run Evaluations de (Berger 1985, 257–61).
Comente a frase “probs maiores, odds menores”.
Comente a frase “custa 1 real apostar 95 centavos com a gente”.
Se neste mercado de 100 bilhões de reais anuais²⁰ o Governo Federal fica com 12% do total arrecadado pelas empresas de apostas, qual o impacto monetário da afirmação do item e no montante recebido pelo Governo Federal? E nas empresas de apostas?
Comente o Art. 17., § II da Lei 14.790²¹.

II - veiculem afirmações infundadas sobre as probabilidades de ganhar ou os possíveis ganhos que os apostadores podem esperar;

3.3.6 Propriedades

Dos axiomas de Kolmogorov resultam algumas propriedades, apresentadas sem demonstração:

P1 (Probabilidade do conjunto vazio) \[\begin{equation} P(\emptyset)=0 \tag{3.21} \end{equation}\]

P2 (Complementar) \[\begin{equation} P(A)=1-P(A^C) \tag{3.22} \end{equation}\]
P3 (Regra da adição) \[\begin{equation} P(A \cup B) = P(A) + P(B) - P(A \cap B) \tag{3.23} \end{equation}\]
P4 (Lei de De Morgan 1, Eq. (3.13))
\[\begin{equation} P(\left[ A \cup B \right]^C) = P(A^C \cap B^C) \tag{3.24} \end{equation}\]
P5 (Lei de De Morgan 2, Eq. (3.14))
\[\begin{equation} P(\left[ A \cap B \right]^C) = P(A^C \cup B^C) \tag{3.25} \end{equation}\]

Exercício 3.7 Demonstre as Eq. (3.21) a (3.25).

Exemplo 3.23 Em um grupo de \(n\) pessoas, \(2 \le n \le 365\), a probabilidade do evento \(A\): ‘pelo menos duas pessoas aniversariarem no mesmo dia e mês’ pode ser calculada pela propriedade do complementar. Considerando um ano de 365 dias equiprováveis como indicado por (Feller 1968, 33) e sem a presença de gêmeos, trigêmeos, etc., a probabilidade do evento \(A^C\): ‘nenhuma pessoa aniversariar no mesmo dia e mês de outra’, é

\[\begin{equation} P(A^C) = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \cdots \times \frac{365-n+1}{365} \tag{3.26} \end{equation}\] Assim, \[\begin{equation} P(A) = 1 - \left( \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \cdots \times \frac{365-n+1}{365} \right) \tag{3.27} \end{equation}\]

aniv <- function(n){
  p <- 1
  for(i in 1:n){
    p <- p*(365-i+1)/365 
  }
  return(1-p)
}
aniv(23)

## [1] 0.5072972

prob <- sapply(1:100, aniv)
plot(1:100, prob, main = 'P(A)', xlab = '', las = 1)
points(c(23, 41, 57), c(aniv(23), aniv(41), aniv(57)), pch = 16, 
       col = 'red')
legend(19, 0.55, '(23, 0.5073)', bty = 'n')
legend(35, 0.91, '(41, 0.9032)', bty = 'n')
legend(51, 0.99, '(57, 0.9901)', bty = 'n')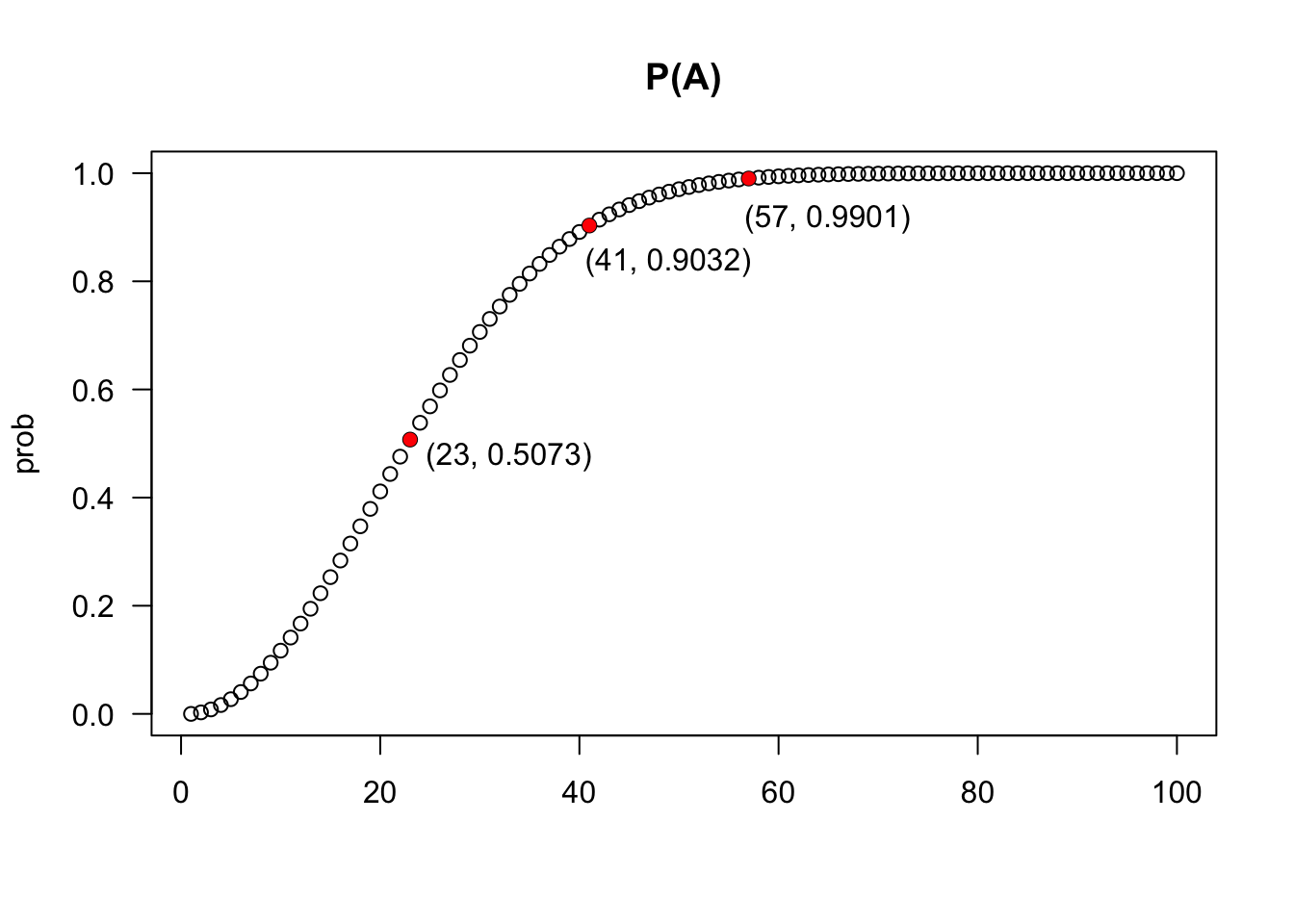

Exemplo 3.24 Em Python.

import matplotlib.pyplot as plt
import numpy as np

def aniv(n):
  """
  Calcula a probabilidade de pelo menos duas pessoas em um grupo 
  de tamanho n fazerem aniversário no mesmo dia.

  Args:
    n: O tamanho do grupo.

  Returns:
    A probabilidade de pelo menos duas pessoas fazerem aniversário 
    no mesmo dia.
  """
  p = 1
  for i in range(1, n + 1):
    p = p * (365 - i + 1) / 365
  return 1 - p

# Calculando a probabilidade para n = 23
print(aniv(23))  # Output: 0.5072972343239854

# Calculando as probabilidades para n de 1 a 100
n_valores = np.arange(1, 101)
prob = np.array([aniv(n) for n in n_valores])

# Plotando o gráfico
plt.plot(n_valores, prob)
plt.xlabel('Número de pessoas')
plt.ylabel('Probabilidade')
plt.title('Probabilidade de Aniversário Compartilhado')

# Destacando pontos específicos
plt.scatter([23, 41, 57], [aniv(23), aniv(41), aniv(57)], 
            color='red')

# Adicionando legendas
plt.text(23, aniv(23) + 0.05, '(23, 0.5073)', ha='center')
plt.text(41, aniv(41) + 0.05, '(41, 0.9032)', ha='center')
plt.text(57, aniv(57) + 0.05, '(57, 0.9901)', ha='center')

plt.show()

Exercício 3.8 Considere os dados do Exemplo 3.23.

Explique em palavras a Eq. (3.26).
Mostre que a Equação (3.26) pode ser escrita como \[\begin{equation} P(A^c) = \left( 1 - \frac{1}{365} \right) \left(1- \frac{2}{365} \right) \cdots \left( 1- \frac{n-1}{365} \right) \tag{3.28} \end{equation}\]
Escreva a função aniv2 implementando a Eq. (3.28) e compare com aniv.
Assista ao vídeo https://www.youtube.com/watch?v=ofTb57aZHZs, gentilmente sugerido por Pedro Devincenzi Ferreira.
Para uma abordagem bayesiana veja (Diaconis and Holmes 2002).

References

Berger, James O. 1985. Statistical Decision Theory and Bayesian Analysis. 2nd ed. Springer Science & Business Media. https://www.springer.com/gp/book/9780387960982.

Cox, Richard T. 1946. “Probability, Frequency and Reasonable Expectation.” American Journal of Physics 14 (1): 1–13. http://www.cs.toronto.edu/~ilya/cox1946.pdf.

De Finetti, Bruno. 1970. “Logical Foundations and Measurement of Subjective Probability.” Acta Psychologica 34: 129–45.

DeGroot, Morris H, and Mark J Schervish. 2012. Probability and Statistics. Pearson Education.

Diaconis, Persi, and Susan Holmes. 2002. “A Bayesian peek into Feller volume I.” Sankhyā: The Indian Journal of Statistics, Series A, 820–41. https://www.jstor.org/stable/25051431.

Feller, William. 1968. An Introduction to Probability Theory and Its Applications Volume I, 3rd Ed. John Wiley & Sons, Inc. https://www.ime.usp.br/~fmachado/MAE5709/FellerV1.pdf.

James, B. R. 2010. “Probabilidade: Um Curso Em Nível Intermediário, Coleção Euclides.” Rio de Janeiro. IMPA, 3a. Edição. https://loja.sbm.org.br/index.php/colecoes/impa/colecao-projeto-euclides/probabilidade-um-curso-em-nivel-intermediario.html.

———. 1985. “Bayesian Methods: General Background.” Maximum Entropy and Bayesian Methods in Applied Statistics, 1–25. https://citeseerx.ist.psu.edu/doc/10.1.1.41.1055.

Kolmogoroff, Andrey. 1933. Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer. https://archive.org/details/kolmogoroff-1933-grundbegriffe-der-wahrscheinlichkeitsrechnung/mode/2up.

Kolmogorov, Andreı̆ Nikolaevich. 1956. Foundations of the Theory of Probability. Chelsea Publishing Company. https://archive.org/details/kolmogorov_202112/mode/2up.

Press, S James. 2003. Subjective and objective Bayesian statistics: Principles, models, and applications, 2nd. edition. John Wiley & Sons. http://primo-pmtna01.hosted.exlibrisgroup.com/PUC01:PUC01:oclc(OCoLC)587388980.

Tahan, Malba. 1938. O Homem Que Calculava. 1st ed. Record, Rio de Janeiro - RJ.

Die Wahrscheinlichkeitstheorie als mathematische Disziplin soll und kann genau in demselben Sinne axiomatisiert werden wie die Geometrie oder die Algebra.↩︎
https://conteudos.xpi.com.br/acoes/relatorios/varejo-xp-como-o-mercado-de-apostas-impacta-o-consumo/↩︎
Art. 17. Sem prejuízo do disposto na regulamentação do Ministério da Fazenda, é vedado ao agente operador de apostas de quota fixa veicular publicidade ou propaganda comercial que: (…)↩︎