8.3 Capítulo 3

Solução. 3.4

\(\Omega_{4} = \{ 1,2,3,4 \}\)
\(\Omega_{6} = \{ 1,2,3,4,5,6 \}\)
\(\Omega_{8} = \{ 1,2,3,4,5,6,7,8 \}\)
\(\Omega_{10} = \{ 1,2,3,4,5,6,7,8,9,10 \}\)
\(\Omega_{12} = \{ 1,2,3,4,5,6,7,8,9,10,11,12 \}\)
\(\Omega_{20} = \{ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 \}\)
\[ \Omega_{4,4} = \left\lbrace \begin{array}{cccccc} (1,1) & (1,2) & (1,3) & (1,4) \\ (2,1) & (2,2) & (2,3) & (2,4) \\ (3,1) & (3,2) & (3,3) & (3,4) \\ (4,1) & (4,2) & (4,3) & (4,4) \\ \end{array} \right\rbrace \]
\[ \Omega_{4,6} = \left\lbrace \begin{array}{cccccc} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) & (1,6) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) & (2,6) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) & (3,6) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) & (4,6) \\ \end{array} \right\rbrace \]

Solução. 3.5
a. \(\frac{1}{2} + \frac{1}{3} + \frac{1}{9}= \frac{17}{18} < 1\)
b. Como o resto da divisão de 35 por 3 é 2, sobram 2 camelos não importa como seja feita a divisão. Note que \(18+12+4=34\).

Solução. 3.7

P4 (Complementar)
Por (3.22) \[ P(\Omega) = 1 \] Pode-se escrever \(\Omega = A \cup A^c\), então \[ P(A \cup A^c) = 1 \] Como \(A \cap A^c = \emptyset\), por (3.23)
\[ P(A \cup A^c) = P(A) + P(A^c) \] Desta forma, \[ P(A) + P(A^c) = 1 \therefore P(A) = 1 - P(A^c) \] \(\bigtriangleup\)
P5
P6
\(A \cup B = A \cup (B-A)\) e \(A \cap (B-A) = \emptyset\). Logo, por (3.23)
\[\begin{equation} P(A \cup B) = P(A) + P(B-A) \tag{1} \end{equation}\] Como \(A \subset B\), \(B = (B-A) \cup (A \cap B)\) e \((B-A) \cap (A \cap B) = \emptyset\). Logo, novamente por (3.23)
\[\begin{equation} P(B) = P(B-A) + P(A \cap B) \tag{2} \end{equation}\] Combinando (1) e (2), \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \] \(\bigtriangleup\)
P7
P8

Solução. 3.11

Solução. 3.13

\(R_D = \{ -5,-4,-3,-2,-1,0,1,2,3,4,5 \}\)
\(R_P = \{ 1,2,3,4,5,6,8,9,10,12,15,16,18,20,24,25,30,36 \}\)
\(R_Q = \left\{ \frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},1,\frac{6}{5},\frac{5}{4},\frac{4}{3},\frac{3}{2},\frac{5}{3},2,\frac{5}{2},3,4,5,6 \right\}\)

Solução. 3.14

\(R_Y = \{ -5,-4,-3,-2,-1,0,1,2,3,4,5 \}\)
\(P(Y=-5) = P(Y=5) = \frac{1}{36}\)
\(P(Y=-4) = P(Y=4) = \frac{2}{36}\)
\(P(Y=-3) = P(Y=3) = \frac{3}{36}\)
\(P(Y=-2) = P(Y=2) = \frac{4}{36}\)
\(P(Y=-1) = P(Y=1) = \frac{5}{36}\)
\(P(Y=0) = \frac{6}{36}\)
De forma geral, \(P(Y=y) = \frac{6-|y|}{36}\).

Solução. 3.15

Solução. 3.18

Sabe-se que \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\). Assim, \[\begin{align*} \sum_{x=0}^{\infty} \frac{e^{-\lambda} \lambda^{x}}{x!} = e^{-\lambda} \sum_{x=0}^{\infty} \frac{\lambda^{x}}{x!} = e^{-\lambda} e^{\lambda} = 1 \end{align*}\]
\[\begin{align*} E(X) = \sum_{x=0}^{\infty} x \frac{e^{-\lambda} \lambda^{x}}{x!} = \lambda e^{-\lambda} \sum_{x=1}^{\infty} \frac{\lambda^{x-1}}{(x-1)!} = \lambda e^{-\lambda} e^{\lambda} = \lambda \end{align*}\]
\[\begin{align*}{lcl} E(X^2) &= \sum_{x=0}^{\infty} x^2 \frac{e^{-\lambda} \lambda^{x}}{x!} = \lambda e^{-\lambda} \sum_{x=1}^{\infty} \frac{x \lambda^{x-1}}{(x-1)!} = \lambda e^{-\lambda} (\lambda+1) e^{\lambda} = \lambda^2 + \lambda \\ V(X) &= (\lambda^2 + \lambda) - (\lambda^2) = \lambda \end{align*}\]

Solução. 3.19

Sabe-se que \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\). Assim,

\[\begin{align*} \sum_{x=0}^{\infty} \left[ \frac{e^{-\lambda_1} \lambda_{1}^{x}}{x!} p + \frac{e^{-\lambda_2} \lambda_{2}^{x}}{x!} (1-p) \right] =& p e^{-\lambda_1} \sum_{x=0}^{\infty} \frac{\lambda_{1}^{x}}{x!} + e^{-\lambda_2} \sum_{x=0}^{\infty} \frac{\lambda_{2}^{x}}{x!} - p e^{-\lambda_2} \sum_{x=0}^{\infty} \frac{\lambda_{2}^{x}}{x!} \\ =& p e^{-\lambda_1} e^{\lambda_1} + e^{-\lambda_2} e^{\lambda_{2}} - p e^{-\lambda_2} e^{\lambda_{2}} \\ =& p + 1 - p \\ =& 1 \end{align*}\]

\[\begin{align*} E(X) =& \sum_{x=0}^{\infty} x \left[ \frac{e^{-\lambda_1} \lambda_{1}^{x}}{x!} p + \frac{e^{-\lambda_2} \lambda_{2}^{x}}{x!} (1-p) \right] \\ =& \lambda_1 p e^{-\lambda_1} \sum_{x=1}^{\infty} \frac{\lambda_{1}^{(x-1)}}{(x-1)!} + \lambda_2 e^{-\lambda_2} \sum_{x=1}^{\infty} \frac{\lambda_{2}^{(x-1)}}{(x-1)!} - \lambda_2 p e^{-\lambda_2} \sum_{x=1}^{\infty} \frac{\lambda_{2}^{(x-1)}}{(x-1)!} \\ =& \lambda_1 p e^{-\lambda_1} e^{\lambda_1} + \lambda_2 e^{-\lambda_2} e^{\lambda_{2}} - \lambda_2 p e^{-\lambda_2} e^{\lambda_{2}} \\ =& \lambda_1 p + \lambda_2 - \lambda_2 p \\ E(X) =& (\lambda_1 - \lambda_2)p + \lambda_2 \end{align*}\]

\[\begin{align*} E(X^2) =& \sum_{x=0}^{\infty} x^2 \left[ \frac{e^{-\lambda_1} \lambda_{1}^{x}}{x!} p + \frac{e^{-\lambda_2} \lambda_{2}^{x}}{x!} (1-p) \right] \\ =& \lambda_1 p e^{-\lambda_1} \sum_{x=1}^{\infty} \frac{x \lambda_{1}^{(x-1)}}{(x-1)!} + \lambda_2 e^{-\lambda_2} \sum_{x=1}^{\infty} \frac{x \lambda_{2}^{(x-1)}}{(x-1)!} - \lambda_2 p e^{-\lambda_2} \sum_{x=1}^{\infty} \frac{x \lambda_{2}^{(x-1)}}{(x-1)!} \\ =& \lambda_1 p e^{-\lambda_1} (\lambda_1+1) e^{\lambda_1} + \lambda_2 e^{-\lambda_2} (\lambda_2+1) e^{\lambda_{2}} - \lambda_2 p e^{-\lambda_2} (\lambda_2+1) e^{\lambda_{2}} \\ =& \lambda_1 p (\lambda_1+1) + \lambda_2 (\lambda_2+1) - \lambda_2 p (\lambda_2+1)\\ E(X^2)=& \lambda_1^2 p + \lambda_1 p + \lambda_2^2 + \lambda_2 - \lambda_2^2 p - \lambda_2 p \\[20pt] V(X) =& \left[ \lambda_1^2 p + \lambda_1 p + \lambda_2^2 + \lambda_2 - \lambda_2^2 p - \lambda_2 p \right] - \left[ \lambda_1 p + \lambda_2 - \lambda_2 p \right]^2 \\ V(X) =& -(\lambda_1 + \lambda_2)^2 p^2 + \left[ (\lambda_1 + \lambda_2)^2 + \lambda_1 -\lambda_2 \right] p + \lambda_2 \end{align*}\]

Solução. 3.24

\(F(X) = 1-e^{-2x}\)
\(P(X<1) = F(1) = 1-e^{-2 \times 1} = 1-e^{-2} \approx 0.8647\)
\(P(X>2) = 1-F(2) = 1-(1-e^{-2 \times 2}) = e^{-4} \approx 0.0183\)

curve(dexp(x), 0, 4)

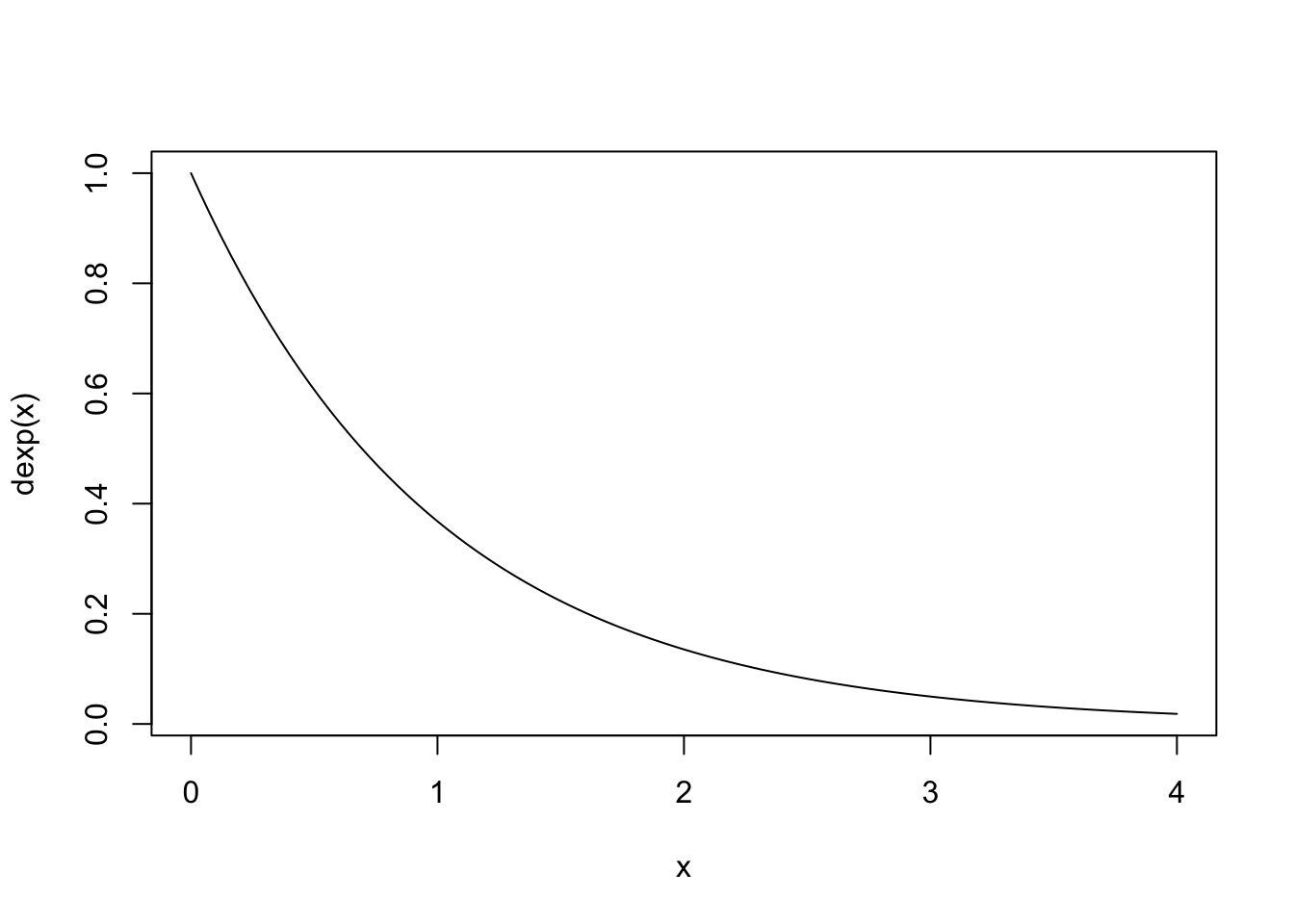
Exemplo 8.4 Em Python.

import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt

# Valores de x
x = np.linspace(0, 4, 100)

# Plotando a curva da distribuição exponencial
plt.plot(x, expon.pdf(x), color='blue')

# Configurações do gráfico
plt.xlabel('x')
plt.ylabel('Densidade')
plt.title('Distribuição Exponencial (taxa = 1)')

plt.show()