5.5 Distribuição a posteriori
A posteriori de hoje é a priori de amanhã. (Máxima bayesiana)
A (distribuição a) posteriori \(\pi(\theta|x)\) é dada por
\[\begin{equation} \pi(\theta|x) = \frac{\pi(\theta) L(\theta|x)}{\pi(x)} \tag{5.5} \end{equation}\]
onde \(\pi(\theta)\) é a (distribuição a) priori de \(\theta\), \(L(\theta|x)\) é a (função de) verossimilhança conforme Eq. (5.1) e a (distribuição) preditiva de \(x\) é \[\begin{equation} \pi(x) = \int_{\theta} \pi(\theta) L(\theta|x) d\theta \tag{5.6} \end{equation}\]
5.5.1 Conjugação
Definição 5.4 Se a posteriori possui a mesma forma paramétrica da priori, chama-se esta priori de distribuição conjugada para a verossimilhança.
Exemplo 5.10 Seja uma moeda com probabilidade \(\theta\) de face cara. A sequência de variáveis aleatórias \(X_1, \ldots, X_n\) tem distribuição Bernoulli com probabilidade \(\theta\) de sucesso, anotada por \(X|\theta \sim Ber(\theta)\). Conforme Eq. (5.2) \[\begin{align*} L(\theta|x) \propto \theta^{s} (1-\theta)^{f}, \end{align*}\]
onde \(s = \sum_{i=1}^n x_i\) e \(f = n-s\) indicam respectivamente o total de sucessos e fracassos observados.
Por conveniência da conjugação, a priori de \(\theta\) é admitida como uma Beta de hiperparâmetros \(\alpha\) e \(\beta\), anotada por \(\theta|\alpha,\beta \sim Beta(\alpha,\beta)\) ou simplificadamente \(\theta \sim Beta(\alpha,\beta)\) conforme Seção 3.9.7. A densidade da priori é portanto \[\begin{align*} \pi(\theta) = \dfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \theta^{\alpha-1} (1-\theta)^{\beta-1} \end{align*}\]
Se desconsiderarmos a constante, pode-se escrever a priori proporcional ao núcleo da função, i.e., a parte que envolve \(\theta\). \[\begin{align*} \pi(\theta) \propto \theta^{\alpha-1} (1-\theta)^{\beta-1} \end{align*}\]
A conveniência em escolher uma verossimilhança Binomial para \(X|\theta\) e uma priori Beta para \(\theta\) reside no fato de estas distribuições serem conjugadas. Ao realizar a operação bayesiana obtém-se uma posteriori Beta com os parâmetros da priori atualizados pelo número total de caras (sucessos) observadas e de coroas (fracassos) na amostra, anotada por \(\theta|X \sim Beta(\alpha+s,\beta+f)\). A posteriori é dada por \[\begin{align*} \pi(\theta|x) &\propto \pi(\theta) L(\theta|x) \\ &\propto \theta^{s} (1-\theta)^{f} \cdot \theta^{\alpha-1} (1-\theta)^{\beta-1} \\ &\propto \theta^{(\alpha+s)-1} (1-\theta)^{(\beta+f)-1} \\ \pi(\theta|x) &= \frac{\Gamma(\alpha+s+\beta+f)}{\Gamma(\alpha+s) \Gamma(\beta+f)} \theta^{(\alpha+s)-1} (1-\theta)^{(\beta+f)-1} \end{align*}\]
Exemplo 5.11 Sejam \(n=12\) lançamentos com 9 sucessos (caras) e 3 fracassos (coroas). Se for considerada uma priori imprópria \(Beta(0,0)\) para \(\theta\), pela conjugação a posteriori é \(\theta|x \sim Beta(0+9,0+3)\).
library(LearnBayes)
prior <- c(0,0) # priori beta(0, 0) para \theta
data <- c(9,3) # 9 sucessos e 3 fracassos
triplot(prior, data, where='topleft')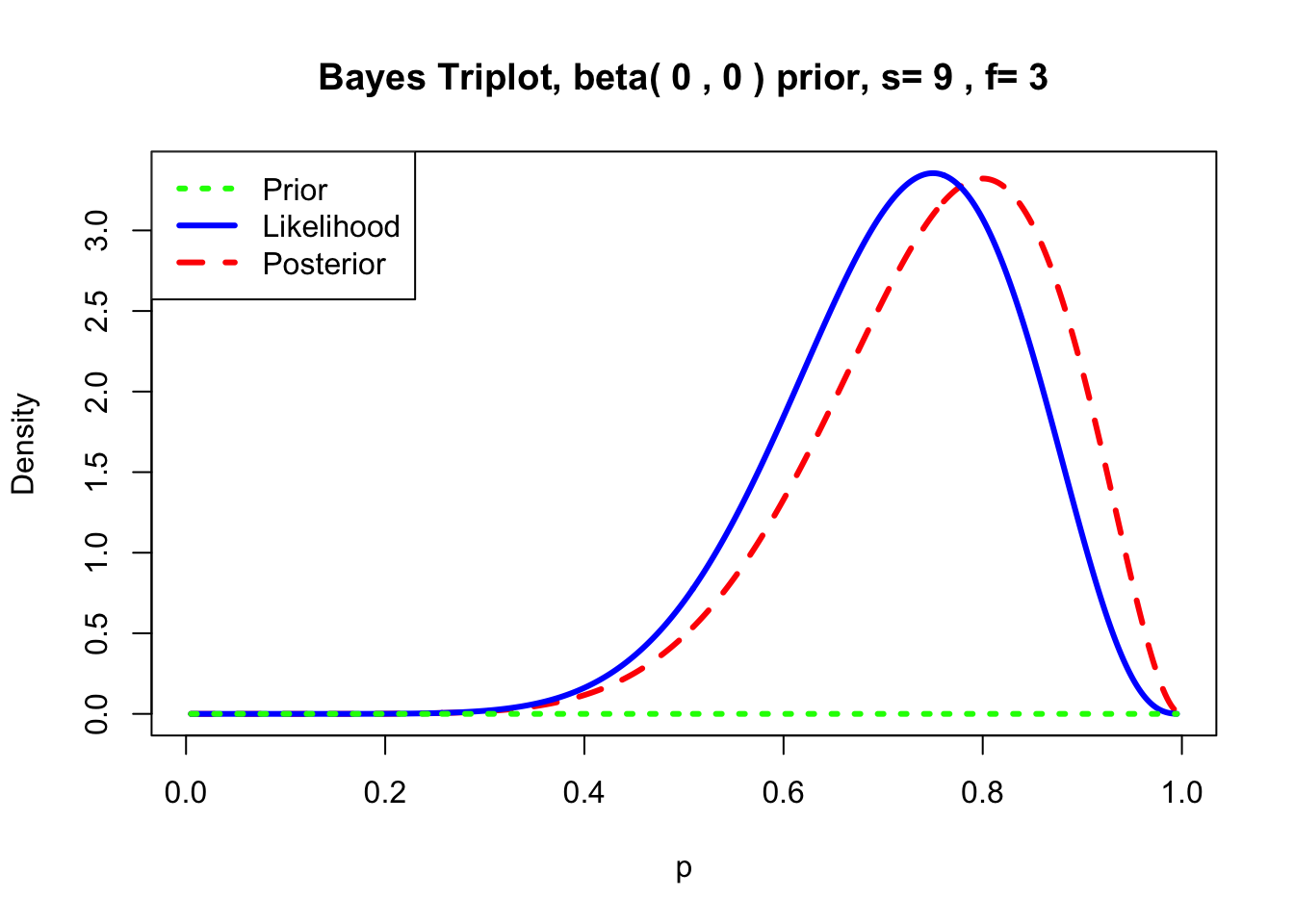
## [1] 0.8Exemplo 5.12 Em Python.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Parâmetros da priori e dos dados
prior = np.array([0, 0]) # priori beta(0, 0)
data = np.array([9, 3]) # 9 sucessos e 3 fracassos
# Calculando os parâmetros da posteriori
posterior = prior + data # posteriori beta(9, 3)
# Criando o gráfico triplot
x = np.linspace(0, 1, 100)
plt.plot(x, beta.pdf(x, prior[0], prior[1]), label='Priori',
color='blue')
plt.plot(x, beta.pdf(x, data[0] + 1, data[1] + 1),
label='Verossimilhança', color='green')
plt.plot(x, beta.pdf(x, posterior[0], posterior[1]),
label='Posteriori', color='red')
plt.xlabel(r'$\theta$')
plt.ylabel('Densidade')
plt.title('Gráfico Triplot')
plt.legend()
plt.show()
# Calculando a moda da posteriori
moda = (posterior[0] - 1) / (posterior[0] + posterior[1] - 2)
print(f"Moda da posteriori: {moda:.4f}") # Output: 0.8000A priori de Jeffreys é uma \(Beta(1/2,1/2)\), assim \(\theta|x \sim Beta(1/2+9,1/2+3)\).
library(LearnBayes)
prior <- c(1/2,1/2) # priori de Jeffreys (arco-seno) para \theta
data <- c(1/2+9,1/2+3) # 9 sucessos e 3 fracassos
triplot(prior, data, where='topleft')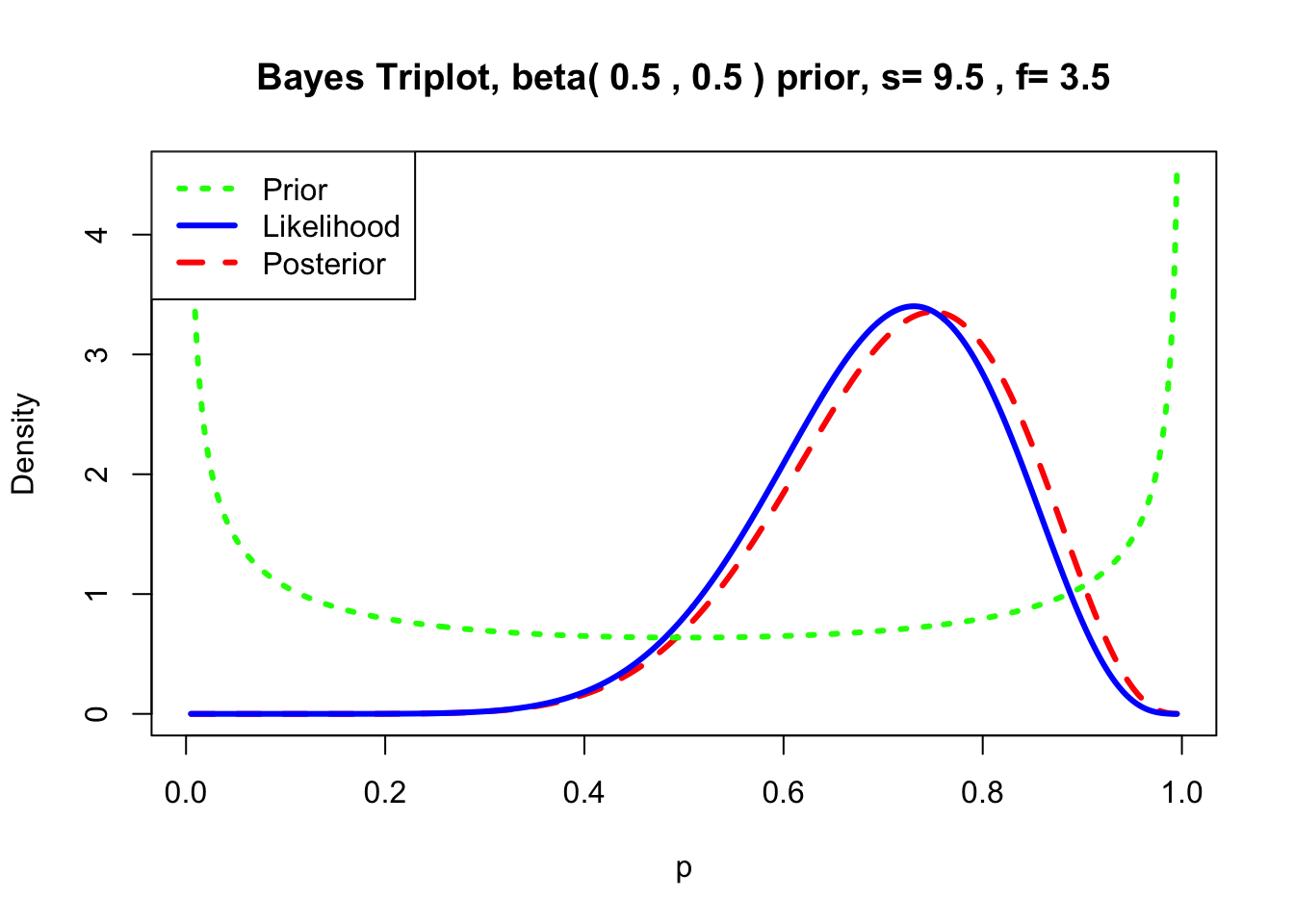
## [1] 0.7727273Exemplo 5.13 Em Python.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Parâmetros da priori e dos dados
prior = np.array([1/2, 1/2]) # priori de Jeffreys beta(1/2, 1/2)
data = np.array([1/2 + 9, 1/2 + 3]) # 9 sucessos e 3 fracassos
# Calculando os parâmetros da posteriori
posterior = prior + data # posteriori beta(10, 4)
# Criando o gráfico triplot
x = np.linspace(0, 1, 100)
plt.plot(x, beta.pdf(x, prior[0], prior[1]), label='Priori',
color='blue')
plt.plot(x, beta.pdf(x,data[0],data[1]), label='Verossimilhança',
color='green')
plt.plot(x, beta.pdf(x, posterior[0], posterior[1]),
label='Posteriori', color='red')
plt.xlabel(r'$\theta$')
plt.ylabel('Densidade')
plt.title('Gráfico Triplot')
plt.legend()
plt.show()
# Calculando a moda da posteriori
moda = (posterior[0] - 1) / (posterior[0] + posterior[1] - 2)
print(f"Moda da posteriori: {moda:.4f}") # Output: 0.7143Exercício 5.8 Considere \(X_1, \ldots, X_n\) uma sequência de v.a. tal que \(X|\theta \sim \mathcal{P}(\theta)\).
- Verifique que a distribução gama (Seção 3.9.8) é conjugada da Poisson.
- Utilize as parametrizações forma/escala (\(k\) e \(\lambda\)) e forma/taxa (\(\alpha\) e \(\beta\)).
5.5.2 Prioris impróprias
[T]he natural noninformative prior is an improper prior, namely one which has infinite mass. (Berger 1985, 81)
É possível obter uma distribuição a posteriori a partir de uma priori \(\pi(\theta)\) imprópria.
Exemplo 5.14 Se \(X \sim N(\theta,\sigma_0^2)\) (\(\sigma_0^2\) conhecido) e a priori imprópria não informativa \(\pi(\theta)=1\). Então a preditiva é dada por \[\pi(x) = \int_{-\infty}^{\infty} 1 \times L(\theta|x) d\theta = \frac{1}{\sigma_0 \sqrt{2\pi}} \int_{-\infty}^{\infty} \exp \left\{-\frac{(x - \theta)^2}{2\sigma_0^2}\right\} d\theta=1\] e \[\pi(\theta|x)=\frac{1 \times L(\theta|x)}{\pi(x)}=\frac{1}{\sigma_0 \sqrt{2\pi}} \int_{-\infty}^{\infty} \exp \left\{-\frac{(\theta-x)^2}{2\sigma_0^2}\right\}.\] Assim, \(\theta|x \sim N(x,\sigma_0^2)\).