3.5 Lei da Probabilidade Total e o Teorema de Bayes

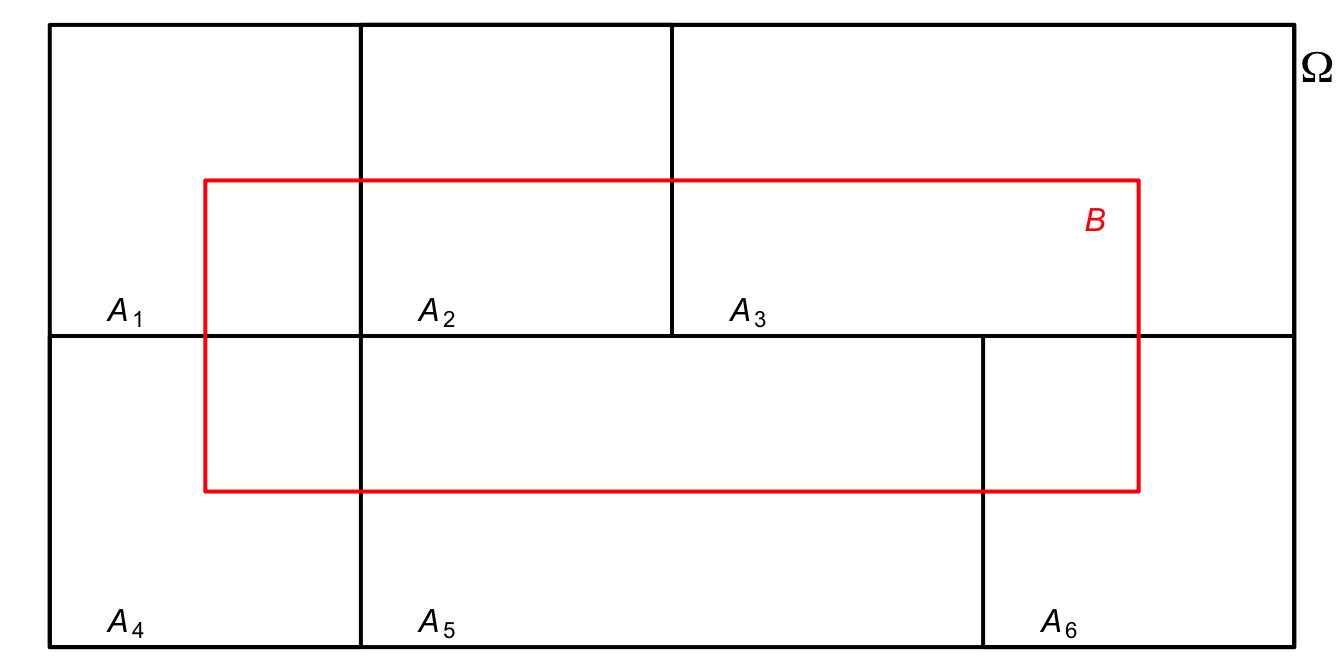
$Partição de $\Omega$.$

Figura 3.1: Partição de $\Omega$.

Considerando a Figura 3.1, pode-se decompor $B$ da seguinte forma:
\[\begin{equation} B = \cup_{i=1}^{6} (A_i \cap B) \end{equation}\]

Teorema 3.1 (Lei da Probabilidade Total) Seja uma sequência enumerável de eventos aleatórios $A_{1}, A_{2}, \ldots, A_{k}$, formando uma partição de $\Omega$. Como as intersecções $A_i \cap B$ são mutuamente excludentes, então de (3.23)

\[\begin{equation} P(B) = \sum_{i=1}^k P(A_i \cap B) \tag{3.37} \end{equation}\]

Aplicando (3.31), pode-se escrever

\[\begin{equation} P(B) = \sum_{i} P(A_{i}) \cdot P(B|A_{i}) \tag{3.38} \end{equation}\]

$\bigtriangleup$

De (3.29) pode-se calcular a probabilidade de $A_{i}$ dada a ocorrência de $B$ por

\[\begin{equation} P(A_{i}|B) = \frac{P(A_{i} \cap B)}{P(B)} \tag{3.39} \end{equation}\]

Aplicando (3.38) no denominador e (3.31) no numerador de (3.39), \[\begin{equation} P(A_{i}|B) = \frac{P(A_{i}) \cdot P(B|A_{i})}{\sum_{j} P(A_{j}) \cdot P(B|A_{j})} \tag{3.40} \end{equation}\]

Este é o Teorema de Bayes (Bayes 1763), útil quando conhecemos as probabilidades condicionais de $B$ dado $A_{i}$, mas não diretamente a probabilidade de $B$. Para uma discussão sobre probabilidade inversa, veja o Capítulo 3 de (Stigler 1986).

Exemplo 3.26 Considere os dados do Exemplo 1.2. É possível calcular $P(D|T)$.
\[\begin{align*} P(D|T) =& \, \frac{P(D) \cdot P(T|D)}{P(D) \cdot P(T|D) + P(\bar{D}) \cdot P(T|\bar{D})} \\ =& \, \frac{0.1 \times 1}{0.1 \times 1 + 0.9 \times 0.1} \\ =& \, \frac{10}{19} \\ P(D|T) \approx& \, 0.5263 \\ \end{align*}\]

Exemplo 3.27 (Teorema de Bayes) Suponha uma caixa com três moedas, uma equilibrada²² e duas com duas faces cara. A probabilidade condicional de a moeda sorteada ter sido a equilibrada pode ser calculada. Para isso pode-se definir $A_{1} :$ ‘a moeda retirada é equilibrada’, $A_{2} :$ ‘a moeda retirada tem duas caras’ e $B :$ ‘o resultado final é cara’ e aplicar a regra de Bayes, resultando em \[ P(A_{1}|B) = \frac{P(A_{1}) \cdot P(B|A_{1})}{P(A_{1}) \cdot P(B|A_{1}) + P(A_{2}) \cdot P(B|A_{2})} = \frac{\frac{1}{3} \times \frac{1}{2}}{\frac{1}{3} \times \frac{1}{2} + \frac{2}{3} \times 1} = \frac{1}{5} = 0.2. \]

pa1 = 1/3
pa2 = 2/3
pba1 = 1/2
pba2 = 1
(pa1b = (pa1*pba1)/(pa1*pba1 + pa2*pba2))

## [1] 0.2

Exemplo 3.28 Em Python.

# Probabilidades
pa1 = 1/3
pa2 = 2/3
pba1 = 1/2
pba2 = 1

# Calculando pa1b
pa1b = (pa1*pba1)/(pa1*pba1 + pa2*pba2)
print(pa1b)  # Output: 0.14285714285714285

Exercício 3.10 Obtenha $P(A_{2}|B)$ pela Eq. (3.40) e verifique que $P(A_{2}|B) = 1-P(A_{1}|B)$.

Exercício 3.11 Considere um teste cuja probabilidade de um falso positivo seja de 2% e a de um falso negativo de 5%. Se uma doença tem 1% de prevalência na população, qual a probabilidade de uma pessoa ter a doença caso o teste dê positivo?

Exercício 3.12 Leia o resumo e faça os exercícios do Capítulo 2 dos Exercícios de Probabilidade do professor Élcio Lebensztayn.

References

Bayes, Thomas. 1763. “An Essay Towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, FRS Communicated by Mr. Price, in a Letter to John Canton, AMFR S.” Philosophical Transactions of the Royal Society of London 1 (53): 370–418. https://www.ias.ac.in/article/fulltext/reso/008/04/0080-0088.

———. 1986. The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press.

Termo técnico indicando que cada moeda possui uma face cara e outra face coroa, ambas com probabilidade $\frac{1}{2}$ de ocorrência.↩︎