3.8 Variáveis Aleatórias Contínuas
3.8.1 Definição
Uma variável aleatória é contínua quando assume qualquer valor em um conjunto não enumerável.
Exemplo 3.43 (Adaptado de (James 2010, 36)) Escolhe-se um ponto ao acaso em \([0,1]\), sendo \(X\) o resultado. Assim, \[ \Omega = [0,1], \;\; X(\omega) = \omega. \]
Exemplo 3.44 (Adaptado de (James 2010, 35)) Escolhe-se um ponto ao acaso em \([0,1]\), sendo \(X\) o quadrado do valor obtido. Assim, \[ \Omega = [0,1], \;\; X(\omega) = \omega^2. \]
3.8.2 Distribuição de probabilidade contínua
Seja \(X\) uma variável aleatória contínua. Como não é possível listar todos os elementos de \(R_{X}\), a notação \(p(x)\) perde o sentido visto que \(p(x)\) é zero para todo \(x \in R_{X}\). Desta forma trabalha-se com uma (função) densidade (de probabilidade) (fdp) \(f(x)\), satisfazendo
\[\begin{equation} f(x) \ge 0, \forall \; x \tag{3.65} \end{equation}\]
\[\begin{equation} \int_{x} f(x)\;dx = 1 \tag{3.66} \end{equation}\]
\[\begin{equation} P(a \leq X \leq b) = \int_{a}^{b} f(x)\;dx \tag{3.67} \end{equation}\]
A (função) distribuição (acumulada) (fda) \(F\) de uma v.a. contínua, é definida como
\[\begin{equation} F(x) = P(X \leq x) = \int_{-\infty}^x f(t) \;dt \tag{3.68} \end{equation}\]
Note que \(f(x)=F'(x)\), \(P(X=x)=0\) e \(P(X \le x) = P(X < x)\).
Exemplo 3.45 (fda) Suponha a v.a. \(X\): ‘altura de pessoas da PUCRS’ com função densidade \[ f(x) = -\frac{46875}{19652} (x^{2} - 3.36x + 2.36), \;\; x \in \left[ 1.00,2.36 \right]. \] Por (3.68), a função distribuição acumulada de \(X\) é
\[\begin{align*} F(x) =& P(X \leq x) \nonumber \\ =& -\frac{46875}{19652} \int_{1}^{x} (t^{2} - 3.36t + 2.36) \;dt \nonumber \\ =& -\frac{46875}{19652} \left[ \frac{t^{3}}{3} - \frac{3.36t^{2}}{2} + 2.36t \right] \bigg\rvert_{1}^{x} \nonumber \\ =& -\frac{46875}{19652} \left( \left[ \frac{x^{3}}{3} - 1.68x^{2} + 2.36x \right] - \left[ \frac{1^{3}}{3} - 1.68 \times 1^{2} + 2.36 \times 1 \right] \right) \nonumber \\ F(x) =& -\frac{46875}{19652} \left[ \frac{x^{3}}{3} - 1.68x^{2} + 2.36x - \frac{76}{75} \right] \nonumber \end{align*}\]
Exemplo 3.46 (Probabilidade com v.a. contínua) Suponha novamente a v.a. do Exemplo 3.45. Aplicando (3.67), \[ P(1.45 \leq X \leq 1.72) = -\frac{46875}{19652} \int_{1.45}^{1.72} (x^{2} - 3.36x + 2.36) \;dx = F(1.72) - F(1.45) \approx 0.2881. \]
Exercício 3.20 Que propriedade está sendo verificada no código abaixo? O que ela indica?
## 1 with absolute error < 1.1e-14Exemplo 3.47 Em Python.
import scipy.integrate as integrate
# Definindo a função f(x)
def f(x):
return (-46875/19652) * (x**2 - 3.36*x + 2.36)
# Calculando a integral definida de f(x) de 1 a 2.36
result = integrate.quad(f, 1, 2.36)
# Imprimindo o resultado
print(result)Exercício 3.21 Considere \(F(x)\) no Exemplo 3.45.
- Escreva uma função em R que represente \(F(x)\), esboçando seu gráfico.
- Repita este procedimento em Python.
3.8.3 Valor esperado
O valor esperado de uma variável aleatória contínua \(X\) é dado por \[\begin{equation} E(X) = \int_{x} x f(x)\;dx \tag{3.69} \end{equation}\]
O valor esperado de uma função \(g(X)\) é dado por \[\begin{equation} E(g(X)) = \int_{x} g(x) f(x)\;dx \tag{3.70} \end{equation}\]
As propriedades se mantêm conforme Seção 3.6.4.1.
Exemplo 3.48 (Valor esperado de v.a. contínuas \(X\) e \(X^2\)) Do Exemplo 3.46 pode-se calcular \[ E(X) = -\frac{46875}{19652} \int_{1.00}^{2.36} x \; (x^{2} - 3.36x + 2.36) \;dx = 1.68. \] Este resultado é coerente dada a simetria da distribuição. Note que \((1.00+2.36)/2 = 1.68\).
f <- function(x){-(46875/19652)*(x^2 - 3.36*x + 2.36)}
curve(f(x),1,2.36,
main = expression(f(x) == -(46875/19652)*(x^2-3.36*x+2.36)))
abline(v = 1.68, col = 'red')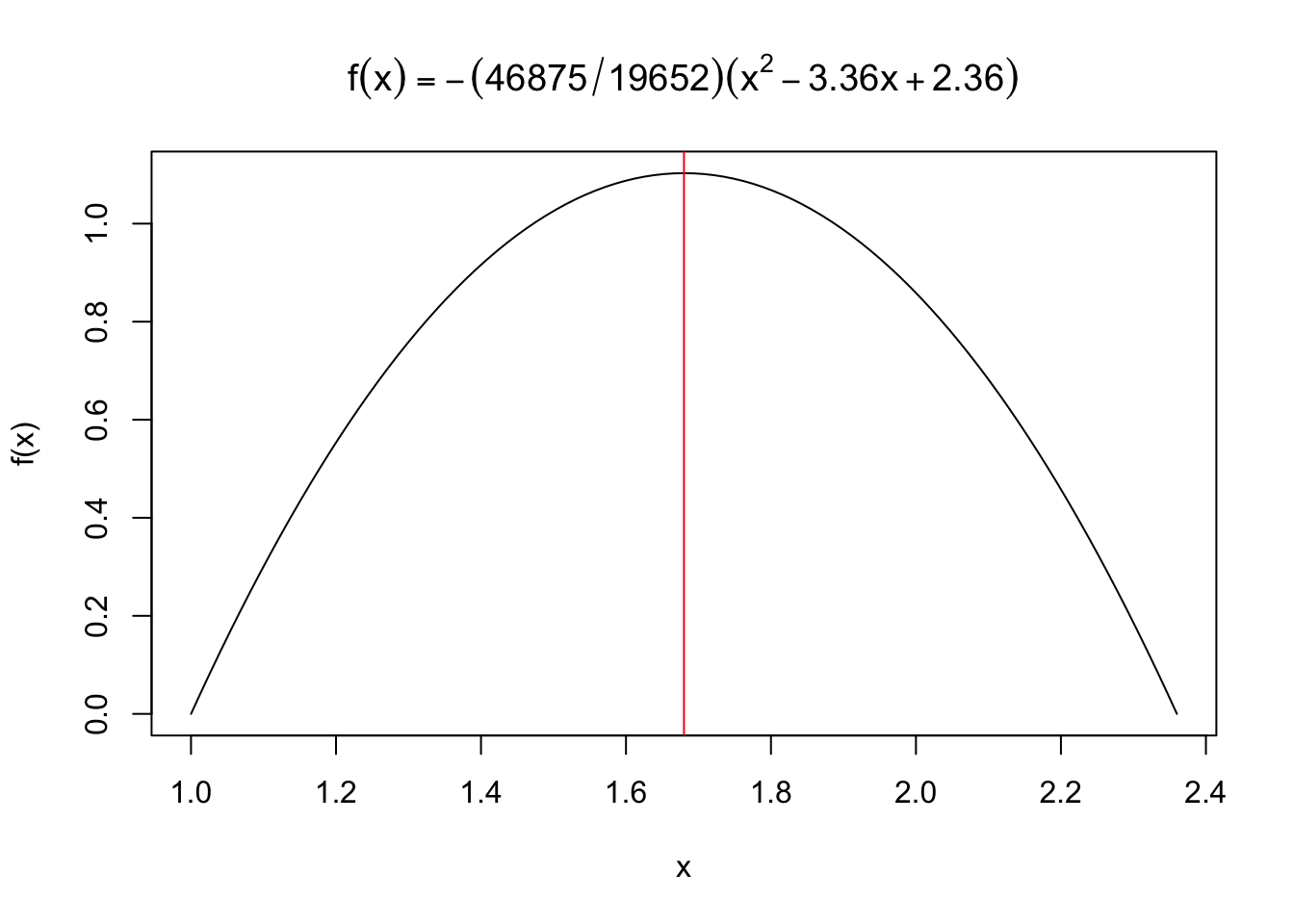
A esperança de \(g(X) = X^2\) é dada por \[ E(X^2) = -\frac{46875}{19652} \int_{1.00}^{2.36} x^2 \; (x^{2} - 3.36x + 2.36) \;dx = 2.91488. \]
Exemplo 3.49 Em Python.
import numpy as np
import matplotlib.pyplot as plt
# Definindo a função f(x)
def f(x):
return -(46875/19652) * (x**2 - 3.36*x + 2.36)
# Plotando a curva
x = np.linspace(1, 2.36, 100)
plt.plot(x, f(x))
# Usando LaTeX para a fórmula
plt.title(r'$f(x) = -\frac{46875}{19652}(x^2 - 3.36x + 2.36)$')
plt.xlabel('x')
plt.ylabel('f(x)')
# Adicionando a linha vertical
plt.axvline(x=1.68, color='red', linestyle='--')
plt.show()Exercício 3.22 Realize os cálculos indicados no Exemplo 3.48.
3.8.4 Variância e desvio padrão
A variância de uma variável aleatória contínua \(X\) é dada tal como no caso discreto indicado pela Eq. (3.43). Da mesma forma o desvio padrão é a raiz quadrada da variância, tal como indicado na Eq. (3.44). As propriedades se mantêm conforme Seção 3.6.4.1.
Exemplo 3.50 (Variância e desvio padrão de uma v.a. contínua) Do Exemplo 3.48 pode-se calcular \[ V(X) = 2.91488 - 1.68^2 = 0.09248 \] \[ D(X) = \sqrt{0.09248} \approx 0.30411 \]