7.1 Correlação
Correlação é uma medida do grau de associação linear entre duas variáveis aleatórias. No senso comum possui uma ampla gama de significados, mas o termo usualmente se refere ao coeficiente de correlação de Pearson, detalhado na Seção 7.1.2.
7.1.1 \(\rho\) \(\cdot\) Correlação universal
(Samuel Kotz et al. 2005, 1375) definem a correlação universal de duas v.a. \(X\) e \(Y\) por
\[\begin{equation}
\rho = Cor(X,Y) = \dfrac{Cov(X,Y)}{D(X) D(Y)},
\tag{7.1}
\end{equation}\]
onde
\[\begin{equation}
Cov(X,Y) = E \left[ (X-E(X)) (Y-E(Y)) \right] = \frac{\sum_{i=1}^N (x_{i} - \mu_{X})(y_{i} - \mu_{Y})}{N}
\tag{7.2}
\end{equation}\]
é a covariância entre \(X\) e \(Y\), \(D(X)\) e \(D(Y)\) são respectivamente os desvios padrão universais de \(X\) e \(Y\) conforme Eq. (2.35) e
\[\begin{equation}
-1 \le \rho \le +1
\end{equation}\]
\[ \Updownarrow \] \[\begin{equation}
0 \le |\rho| \le +1.
\end{equation}\]
- Se \(|\rho| = +1\), então existe uma relação linear da forma \(Y = \beta_0 + \beta_1 X\).
- Se \(\rho = +1\), \(\beta_1 >0\); se \(\rho = -1\), \(\beta_1 <0\).
- Se \(X\) é independente de \(Y\), então \(\rho = 0\), mas o contrário não é necessariamente verdadeiro.
7.1.2 \(r\) \(\cdot\) Coeficiente de Correlação de Pearson
O coeficiente de correlação (amostral) de Pearson foi desenvolvido por Karl Pearson e William Fleetwood Sheppard “antes do final de 1897”, conforme relatado por (Pearson 1920, 44). Denotado por \(r\), pode ser obtido por qualquer das equações a seguir.
\[\begin{equation} r = \frac{1}{n-1} \sum_{i=1}^{n} \left( \dfrac{x_{i} - \bar{x}}{s_{x}} \right) \left( \dfrac{y_{i} - \bar{y}}{s_{y}} \right) \tag{7.3} \end{equation}\]
\[\begin{equation} r = \frac{\sum (x - \bar{x})(y - \bar{y})}{\sqrt{\sum (x - \bar{x})^2 \sum (y - \bar{y})^2}} \tag{7.4} \end{equation}\]
\[\begin{equation} r = \frac{n \sum{x y} - \sum{x} \sum{y}}{\sqrt{[n \sum{x^2} - (\sum{x})^2] [n \sum{y^2} - (\sum{y})^2]}} \tag{7.5} \end{equation}\]
onde \[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i}, \;\; s_{x}^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_{i} - \bar{x}) ^2 \] \[ \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_{i}, \;\; s_{y}^2 = \frac{1}{n-1} \sum_{i=1}^{n} (y_{i} - \bar{y}) ^2 \] \[ -1 \le r \le +1 \]
Note pela Equação (7.3) que \(r\) é uma média dos produtos dos pares ordenados \((x_{i}, y_{i})\) padronizados, com \(i \in \lbrace 1, 2, \ldots, n \rbrace\). Se os pares de produto positivo predominarem, \(r\) será positivo; se houver predominância dos pares de produto negativo, \(r\) será negativo. Esta estrutura é chamada de momento-produto. A Equação (7.4) remete à definição (7.1), enquanto a Equação (7.5) é útil para a realização dos cálculos.
Exemplo 7.1 Considere a idéia de estimar o número de garrafas de bebida a serem geladas dependendo da temperatura máxima do dia. Seja \(X\): ‘temperatura máxima do dia em \(^{\circ}{\rm C}\)’ e \(Y\): ‘número de garrafas de bebida consumidas’, observadas conforme tabela a seguir.
| \(i\) | \(x_{i}\) | \(y_{i}\) | \(i\) | \(x_{i}\) | \(y_{i}\) | \(i\) | \(x_{i}\) | \(y_{i}\) |
|---|---|---|---|---|---|---|---|---|
| 1 | 29.5 | 146 | 11 | 28.5 | 183 | 21 | 40.9 | 233 |
| 2 | 31.3 | 170 | 12 | 28.0 | 158 | 22 | 28.6 | 169 |
| 3 | 34.7 | 167 | 13 | 36.7 | 181 | 23 | 36.1 | 192 |
| 4 | 40.4 | 244 | 14 | 31.5 | 123 | 24 | 27.1 | 106 |
| 5 | 28.4 | 159 | 15 | 38.1 | 223 | 25 | 29.5 | 170 |
| 6 | 40.3 | 195 | 16 | 33.5 | 176 | 26 | 31.6 | 167 |
| 7 | 41.1 | 225 | 17 | 37.2 | 196 | 27 | 25.2 | 133 |
| 8 | 36.2 | 206 | 18 | 41.9 | 238 | 28 | 31.5 | 138 |
| 9 | 35.7 | 200 | 19 | 31.5 | 184 | 29 | 39.8 | 199 |
| 10 | 26.1 | 134 | 20 | 38.2 | 213 | 30 | 30.8 | 172 |
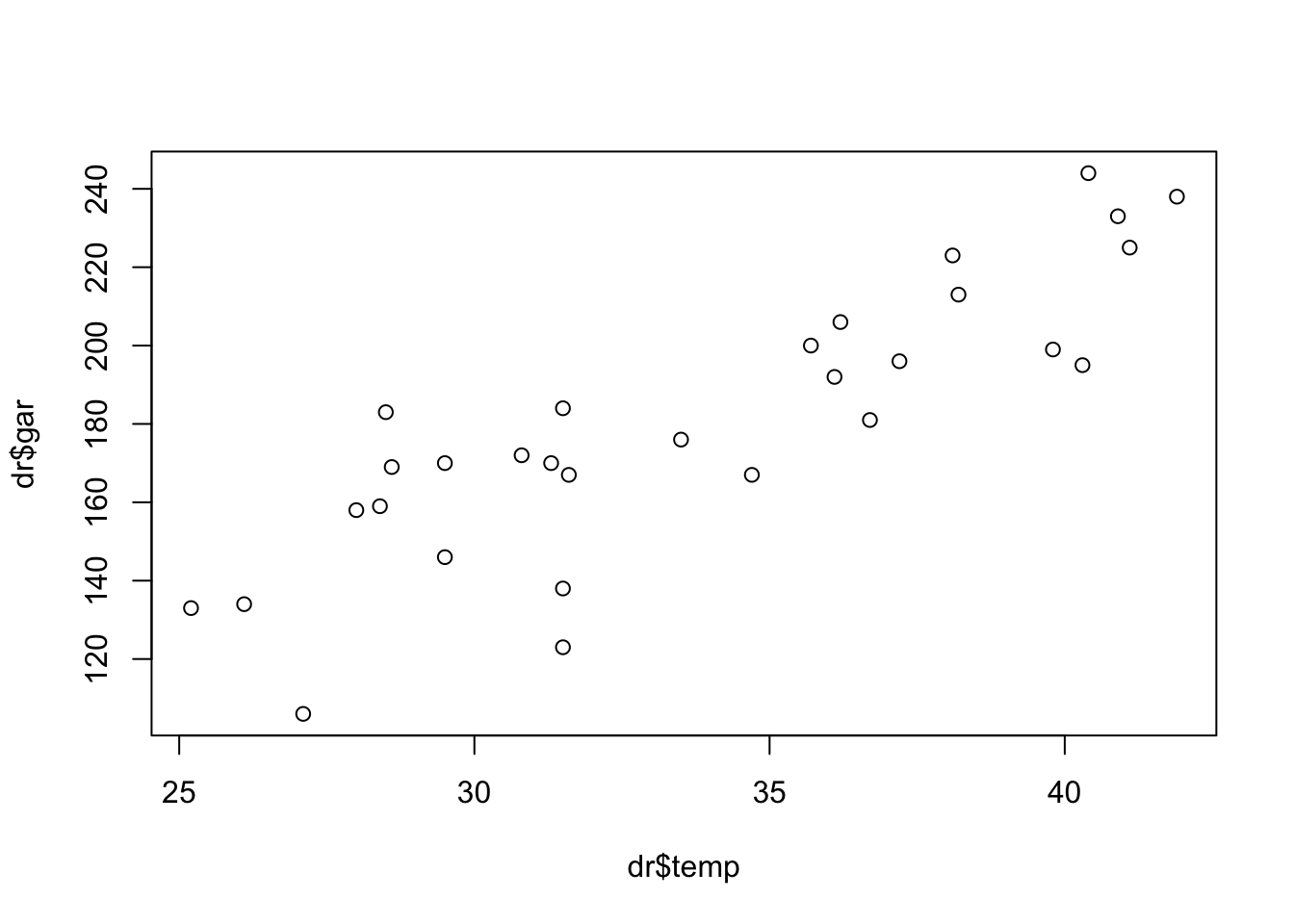
O grau de alinhamento das variáveis pode ser estimado pelo coeficiente de correlação de Pearson, bastando calcular \[ \sum{x} = 1010, \; \sum{x}^2 = 34730, \] \[ \sum{y} = 5400, \; \sum{y}^2 = 1006954, \] \[ \sum{x y} = 186117, \; n=30 \]
e substituir na Equação (7.5), resultando em
\[r = \frac{30 \times 186117 - 1010 \times 5400}{\sqrt{[30 \times 34730 - 1010^2] [30 \times 1006954 - 5400^2]}} \approx 0.8564926\]
## [1] 0.8564926É possível obter o valor de \(r\) a partir da função stats::lm. Ela calcula o coeficiente de determinação \(r^2\) conforme Seção 7.2.3.6, que no modelo RLS (Seção 7.2) é o quadrado de \(r\). Logo \(r=\sqrt{r^2}\).
f <- lm(dr$gar ~ dr$temp) # Modelo RLS
r2 <- summary(f)$r.squared # Extraindo r2
sqrt(r2) # r, a correlação de Pearson## [1] 0.8564926## [1] TRUEExemplo 7.2 Em Python.
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
# Carrega os dados
try:
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt',
sep=' ')
except Exception as e:
print(f"Erro ao carregar o arquivo: {e}")
exit()
# Gráfico de dispersão
plt.scatter(dr['temp'], dr['gar'])
plt.xlabel('temp')
plt.ylabel('gar')
plt.title('Gráfico de Dispersão entre temp e gar')
plt.show()
# Calcula a correlação
correlacao = dr['temp'].corr(dr['gar'])
print(f"Correlação (usando pandas .corr()): {correlacao}")
# Modelo de regressão linear
X = dr['temp'] # Variável independente
y = dr['gar'] # Variável dependente
# Adiciona uma coluna de 1s para o intercepto
X = np.column_stack((np.ones(len(X)), X))
# Realiza a regressão linear usando statsmodels
import statsmodels.api as sm
model = sm.OLS(y, X).fit()
r2 = model.rsquared
r = np.sqrt(r2)
print(f"R-squared: {r2}")
print(f"Correlação (via modelo linear): {r}")
# Comparação com tolerância devido a possíveis diferenças de precisão
tolerancia = 1e-9 # Define uma pequena tolerância
comparacao = np.allclose(correlacao, r, atol=tolerancia)
print(f"Comparação entre correlação direta e via modelo linear: {comparacao}")
# Teste de correlação de Pearson (usando scipy.stats)
pearson_coef, p_value = stats.pearsonr(dr['temp'], dr['gar'])
print(f"Coeficiente de Pearson (usando scipy.stats): {pearson_coef}")
print(f"Valor-p do teste de correlação: {p_value}")Exercício 7.1 Calcule o valor de \(r\) com os dados do Exemplo 7.1 a partir das Equações (7.3) e (7.4). Compare com os valores obtidos via Eq. (7.5) e pelas funções stats::cor() e pandas.DataFrame.corr().
Exercício 7.2
- Analise o quarteto de Anscombe (Anscombe 1973) e a documentação de
datasets::anscombe. - Acesse datasauRus46.
- Acesse Bivariate Correlation Simulation and Bivariate Scatter Plotting47 e faça simulações variando os parâmetros, observando os gráficos resultantes.
7.1.3 Teste para \(\rho\)
O teste básico é comparar \(\rho\) com zero, que indica ausência completa de alinhamento entre as variáveis. Assim, testa-se \(H_0: \rho = 0\) (não há correlação) vs \(H_1: \rho \ne 0\) (há correlação), denotado por
\[ \left\{ \begin{array}{l} H_0: \rho = 0 \\ H_1: \rho \ne 0\\ \end{array} \right. . \]
Sob \(H_0\) considerando o modelo RLS (Seção 7.2), \[\begin{equation} T = \frac{r}{\sqrt{\frac{1-r^2}{n-2}}} \sim t_{n-2}. \tag{7.6} \end{equation}\]
Exercício 7.3 A partir da Eq. (7.6), mostre que \(T = r \sqrt{\frac{n-2}{1-r^2}}\).
Exemplo 7.3 (Verificando o alinhamento no modelo RLS) Considere novamente as informações apresentadas no Exemplo 7.1. Considerando a estimativa do modelo \(y = -19.11 + 5.91 x\), pode-se testar \(H_0: \rho = 0\) vs \(H_1: \rho \ne 0\). Neste caso \(gl=30-2=28\), \(T \sim t_{28}\) e sob \(H_0\) \[ T = 0.8565 \sqrt{\frac{30-2}{1-0.8565^2}} \approx 8.78. \]
## [1] 0.8564926## [1] 8.780493## [1] 1.565265e-09##
## Pearson's product-moment correlation
##
## data: dr$temp and dr$gar
## t = 8.7805, df = 28, p-value = 1.565e-09
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7176748 0.9298423
## sample estimates:
## cor
## 0.8564926## [1] TRUEExemplo 7.4 Em Python.
import numpy as np
from scipy.stats import t
import pandas as pd
# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt',
sep = '\t')
# Parâmetros
n = 30 # Tamanho da amostra (deve ser consistente com os dados)
gl = n - 2 # Graus de liberdade
# Calculando a correlação (r)
r = np.corrcoef(dr['temp'], dr['gar'])[0, 1]
print(f"Correlação de Pearson (r): {r:.4f}") # Output: 0.9896
# Calculando a estatística t
Tt = r * np.sqrt(gl / (1 - r**2))
print(f"Estatística t (Tt): {Tt:.4f}") # Output: 22.6639
# Calculando o p-value
p_value = 2 * t.cdf(-abs(Tt), df=gl)
print(f"p-value: {p_value:.4f}") # Output: 0.0000
# Usando a função pearsonr (similar a cor.test)
from scipy.stats import pearsonr
corr, p_value = pearsonr(dr['temp'], dr['gar'])
print(f"\nTeste de correlação (pearsonr): r = {corr:.4f}, p = {p_value:.4f}")7.1.4 Intervalo de Confiança para \(\rho\)
Passo 1: Obtenha a transformação z de Fisher (Ronald A. Fisher 1921, 210).
\[\begin{equation} z_r = \frac{1}{2} \ln \left( \frac{1+r}{1-r} \right) = \tanh^{-1}(r) \tag{7.7} \end{equation}\]
Passo 2: Obtenha os limitantes inferior e superior transformados com a confiança desejada \(1-\alpha\).
\[\begin{equation} L = z_r - \frac{z_{1-\alpha/2}}{\sqrt{n-3}} \tag{7.8} \end{equation}\]
\[\begin{equation} U = z_r + \frac{z_{1-\alpha/2}}{\sqrt{n-3}} \tag{7.9} \end{equation}\]
Passo 3: Obtenha o intervalo de confiança \(1-\alpha\) para \(\rho\).
\[\begin{equation} IC[\rho, 1-\alpha] = \left[ \frac{e^{2L}-1}{e^{2L}+1}, \frac{e^{2U}-1}{e^{2U}+1} \right] = [ \tanh L, \tanh U ] \tag{7.10} \end{equation}\]
Exemplo 7.5 Considerando os dados do Exemplo 7.3 pode-se obter o IC 95% para a correlação.
## [1] 1.280029## [1] 0.3772022## [1] 0.9028267## [1] 1.657231## [1] 0.7176715## [1] 0.9298433Exemplo 7.6 Em Python.
import numpy as np
from scipy.stats import norm
# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt',
sep = '\t')
# Calculando a correlação (r)
r = np.corrcoef(dr['temp'], dr['gar'])[0, 1]
# Passo 1: Transformação de Fisher
zr = np.arctanh(r)
print(f"zr: {zr:.4f}") # Output: 2.0644
# Passo 2: Calculando o intervalo de confiança para zr
n = len(dr) # Tamanho da amostra
ep = 1.96 / np.sqrt(n - 3)
L = zr - ep
U = zr + ep
print(f"Intervalo de confiança para zr: [{L:.4f}, {U:.4f}]")
# Passo 3: Transformação inversa de Fisher
L_r = np.tanh(L)
U_r = np.tanh(U)
print(f"Intervalo de confiança para r: [{L_r:.4f}, {U_r:.4f}]")Exercício 7.4
7.1.5 \(\rho_{*}\) e \(r_{*}\) \(\cdot\) Correlação na RPO
Existe um caso especial de cálculo de correlação chamado Regressão Pela Origem (RPO), baseado no modelo conforme Eq. (7.17). Neste caso calcula-se \(r_{*}\) através da expressão
\[\begin{equation} r_{*} = \sqrt{\dfrac{\sum \hat{y}_{i}^2}{\sum y_{i}^2}}, \tag{7.11} \end{equation}\]
tal que \(\hat{y}_{i} = \hat{\beta}_1^{*}x_i\).
Exemplo 7.7 (Correlação na RPO) Considere as informações do Exemplo 7.1. Pode-se calcular \[ r_{*} = \sqrt{\dfrac{997410.3}{1006954}} = \sqrt{0.9905222} \approx 0.9952498. \]
## [1] 0.9952498Exemplo 7.8 Em Python.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
# Downloading data
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt',
sep = '\t')
# Fit the linear model without an intercept
X = dr[['temp']] # Independent variable (temp)
y = dr['gar'] # Dependent variable (gar)
# Use fit_intercept=False to remove intercept
f = LinearRegression(fit_intercept=False)
f.fit(X, y)
yhat = np.sum(f.predict(X)**2) # Sum of squared fitted values
y2 = np.sum(dr['gar']**2) # Sum of squared actual values
result = np.sqrt(yhat / y2)
print(result)
# Alternative using statsmodels (more similar to R's lm)
import statsmodels.api as sm
# Add a constant (even though we'll remove it later)
X_with_const = sm.add_constant(X)
# Fit the model *without* an intercept
f_sm = sm.OLS(y, X_with_const[:, 1:]).fit() # Fit without intercept
yhat_sm = np.sum(f_sm.fittedvalues**2)
y2_sm = np.sum(dr['gar']**2)
result_sm = np.sqrt(yhat_sm / y2_sm)
print(result_sm)É possível obter o valor de \(r_{*}\) a partir da função stats::lm(). Ela calcula o coeficiente de determinação \(r_{*}^2\), que no modelo RPO é o quadrado de \(r_{*}\). Logo \(r_{*}=\sqrt{r_{*}^2}\).
f_rpo <- lm(dr$gar ~ dr$temp - 1) # Modelo RPO
r2_rpo <- summary(f_rpo)$r.squared # Função para obter r2_RPO
sqrt(r2_rpo) # r_RPO## [1] 0.9952498## [1] TRUEExemplo 7.9 Em Python.
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt',
sep = '\t')
# Ajustando o modelo RPO (Regressão Pela Origem)
f_rpo = smf.ols('gar ~ temp - 1', data=dr).fit()
# Extraindo o R^2 do modelo RPO
r2_rpo = f_rpo.rsquared
print(f"R^2 RPO: {r2_rpo:.4f}") # Output: 0.9793
# Calculando r_RPO
r_rpo = np.sqrt(r2_rpo)
print(f"r_RPO: {r_rpo:.4f}") # Output: 0.9896
# Comparando com o r_rpo calculado anteriormente
razao = yhat / y2 # yhat e y2 do exemplo anterior
print(np.isclose(np.sqrt(razao), r_rpo)) # Output: True7.1.6 Teste para \(\rho_{*}\)
Se considerarmos o modelo RPO conforme Eq. (7.17), pode-se testar as hipóteses
\[ \left\{ \begin{array}{l} H_0: \rho_{*} = 0 \\ H_1: \rho_{*} \ne 0\\ \end{array} \right. . \]
Sob \(H_0\), a estatística do teste é \[\begin{equation} T_{*} = \frac{r_{*}}{\sqrt{\frac{1-r_{*}^2}{n-1}}} \sim t_{n-1}. \tag{7.12} \end{equation}\]
Exemplo 7.10 (Verificando o alinhamento no modelo RPO) Considere novamente as informações apresentadas no Exemplo 7.1. Se a estimativa do modelo RPO é \(y = 5.36 x\), pode-se testar
\[ \left\{ \begin{array}{l} H_0: \rho^{*} = 0 \\ H_1: \rho^{*} \ne 0\\ \end{array} \right. \]
Neste caso \(gl=30-1=29\), \(T \sim t_{29}\) e sob \(H_0\) \[ T = 0.9952 \sqrt{\frac{30-1}{1-0.9952^2}} \approx 55.05. \]
## [1] 0.9952498## [1] 55.05267## [1] 6.778938e-31Exemplo 7.11 Em Python.
import numpy as np
from scipy.stats import t
# Parâmetros (se ainda não estiverem definidos)
n = 30 # Tamanho da amostra (deve ser consistente com os dados)
gl_rpo = n - 1 # Graus de liberdade para RPO
# r_rpo (do exemplo anterior)
r_rpo = np.sqrt(yhat / y2) # yhat e y2 do exemplo anterior
print(f"r_rpo: {r_rpo:.4f}") # Output: 0.9896
# Calculando a estatística t para RPO
Tt_rpo = r_rpo * np.sqrt(gl_rpo / (1 - r_rpo**2))
print(f"Estatística t (Tt_rpo): {Tt_rpo:.4f}") # Output: 24.0041
# Calculando o p-value
p_value = 2 * t.cdf(-abs(Tt_rpo), df=gl_rpo)
print(f"p-value: {p_value:.4f}") # Output: 0.0000