3.9 Distr. Contínuas Especiais

Para maiores detalhes recomenda-se (Johnson, Kotz, and Balakrishnan 1994) e (Johnson, Kotz, and Balakrishnan 1995). McLaughlin (2016) traz um compêndio de distribuições de probabilidade.

3.9.1 Uniforme Contínua \(\cdot \; \mathcal{U}(a,b)\)

The uniform distribution is so natural a conception that it has probably been in use far more than can be inferred from printed records. Among such records we may mention, in particular, descriptions of the use of the distribution by (Bayes 1763) and (Pierre Simon Laplace 1812). (Johnson, Kotz, and Balakrishnan 1995, 278)

A distribuição uniforme no intervalo \(\left[ a,b \right]\) tem sua função densidade definida por

\[\begin{equation} f(x|a,b) = \frac{1}{b-a} \tag{3.71} \end{equation}\]

onde \(-\infty < a < b < \infty\) e \(a \le x \le b\).

Função distribuição acumulada

\[\begin{equation} F(x|a,b) = \frac{x-a}{b-a} \tag{3.72} \end{equation}\]

Esperança \[\begin{equation} E(X) = \frac{a+b}{2} \tag{3.73} \end{equation}\]

Variância \[\begin{equation} V(X) = \frac{(b-a)^2}{12} \tag{3.74} \end{equation}\]

Exemplo 3.51 A distribuição uniforme contínua pode ser operada com as funções stats::dunif() (densidade), stats::punif() (probabilidade acumulada), stats::qunif() (quantil) e stats::runif() (aleatório/random).

# P(X < 2) em uma U(1,4)
punif(2, 1, 4)
## [1] 0.3333333
# quantil que limita 2.5% em uma U(1,4)
qunif(0.025, 1, 4)
## [1] 1.075
# simulando 1000 valores pseudo aleatórios de uma U(1,4)
set.seed(999); x <- runif(1000, 1, 4)
summary(x)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.014   1.710   2.486   2.484   3.255   3.999
# densidade de uma U(1,4), sobrepondo valores simulados
hist(x, freq = FALSE, main = 'U(1,4)')
curve(dunif(x,1,4), add = TRUE, col = 'red')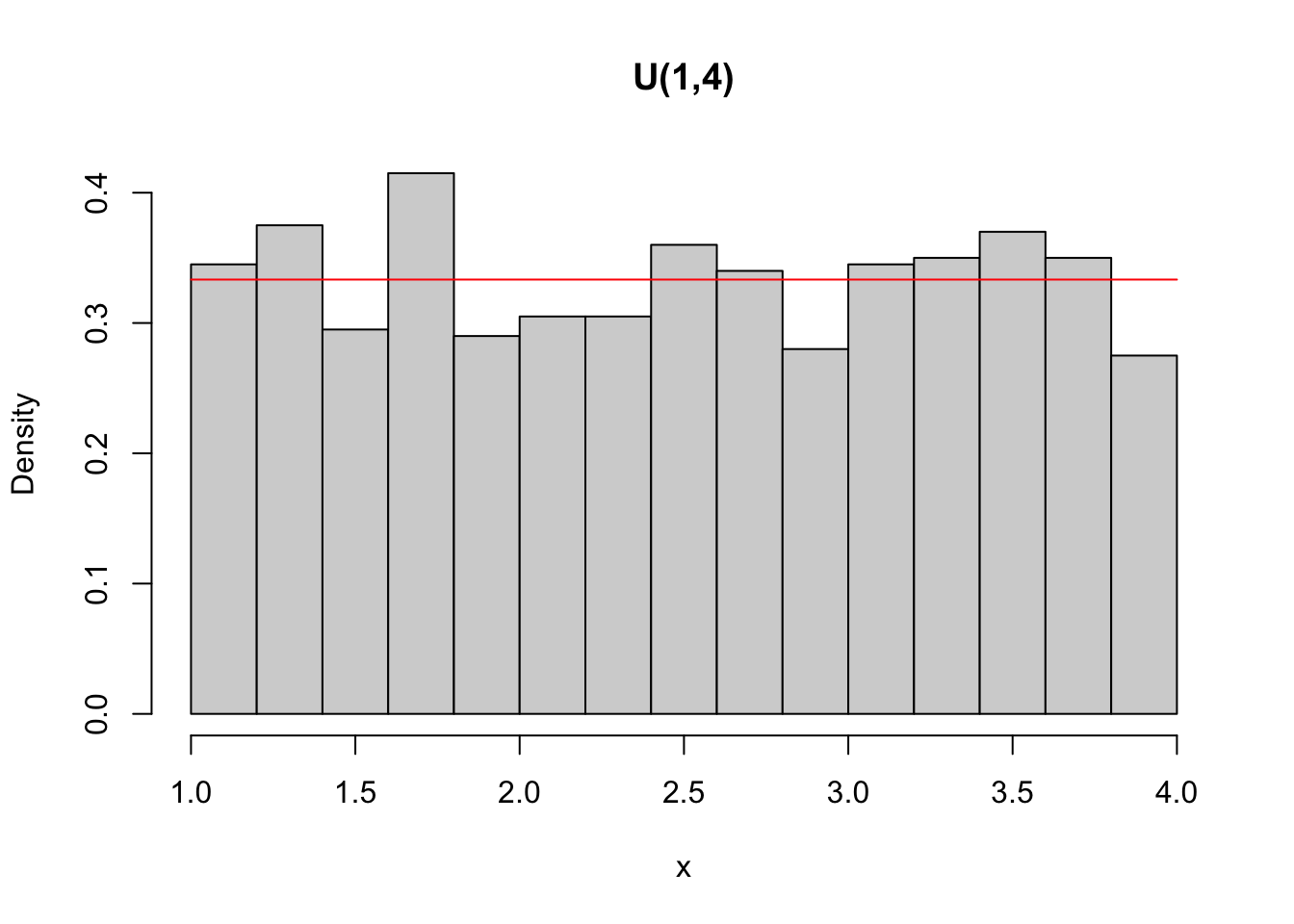

Exemplo 3.52 Em Python.

import numpy as np
from scipy.stats import uniform
import matplotlib.pyplot as plt

# P(X < 2) em uma U(1,4)
prob = uniform.cdf(2, loc=1, scale=3)  # scale = 4 - 1 = 3
print(prob)  # Output: 0.3333333333333333

# Quantil que limita 2.5% em uma U(1,4)
quantil = uniform.ppf(0.025, loc=1, scale=3)
print(quantil)  # Output: 1.075

# Simulando 1000 valores pseudo aleatórios de uma U(1,4)
np.random.seed(999)
x = uniform.rvs(size=1000, loc=1, scale=3)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma U(1,4), sobrepondo valores simulados
plt.hist(x, density=True, bins='auto', color='lightgray', 
         edgecolor='black')
plt.title('U(1,4)')

# Curva da densidade uniforme teórica
x_range = np.linspace(x.min(), x.max(), 100)
plt.plot(x_range, uniform.pdf(x_range,loc=1,scale=3), color='red')

plt.show()

Exercício 3.23 Demonstre as Equações (3.72), (3.73) e (3.74) considerando as identidades (3.75) e (3.76).

\[\begin{equation} a^2 - b^2 = (a-b)(a+b) \tag{3.75} \end{equation}\]

\[\begin{equation} a^3 - b^3 = (a-b)(a^2+ab+b^2) \tag{3.76} \end{equation}\]

3.9.2 Exponencial \(\cdot \; \mathcal{E}(\lambda)\)

Now if a practical model can be assumed to be a renewal process then in order to reduce it to a Poisson process it is required to characterize its interval distribution \(F(x)\) to be exponential. (Galambos and Kotz 1978, 66)

A distribuição exponencial descreve a probabilidade do tempo entre eventos que ocorrem de forma contínua, independente e com uma taxa média constante, como os descritos por um processo de Poisson. A variável aleatória contínua \(X\) tem distribuição exponencial de parâmetro \(\lambda\), denotada por \(X \sim \mathcal{E}(\lambda)\), se possui uma função densidade na forma \[\begin{equation} f(x|\lambda) = \lambda e^{-\lambda x} \tag{3.77} \end{equation}\] onde \(\lambda > 0\) indica o parâmetro de taxa e \(x > 0\). Sua função distribuição acumulada é dada por \[\begin{equation} F(x|\lambda) = 1 - e^{-\lambda x} \tag{3.78} \end{equation}\] A esperança e variância são dadas por \[\begin{equation} E(X)= \frac{1}{\lambda} \tag{3.79} \end{equation}\] \[\begin{equation} V(X)=\frac{1}{\lambda^2} \tag{3.80} \end{equation}\]

Exemplo 3.53 A distribuição exponencial pode ser operada com as funções stats::dexp() (densidade), stats::pexp() (probabilidade acumulada), stats::qexp() (quantil) e stats::rexp() (aleatório/random).

# P(X < 0.6) em uma exponencial de taxa 2
pexp(0.6, 2)
## [1] 0.6988058
# quantil que limita 2.5% em uma exponencial de taxa 2
qexp(0.025, 2)
## [1] 0.0126589
# simulando 1000 valores pseudo aleatórios de uma Exp(2)
set.seed(999); x <- rexp(1000, 2)
summary(x)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000549 0.1467337 0.3490276 0.5025402 0.7075559 2.7126404
# densidade de uma Exp(2), sobrepondo valores simulados
hist(x, freq = FALSE, main = 'Exp(2)')
curve(dexp(x,2), add = TRUE, col = 'red')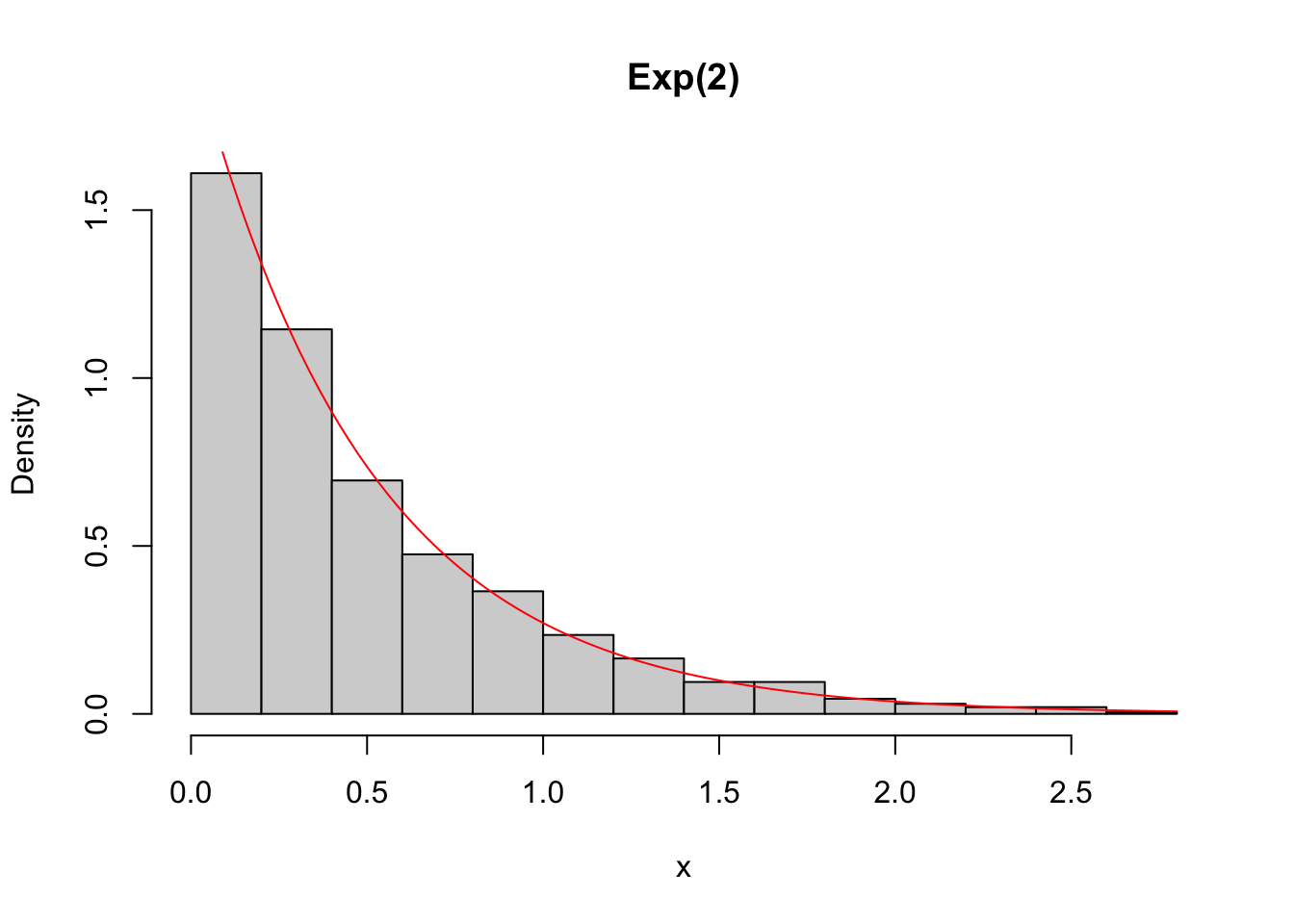

Exemplo 3.54 Em Python.

import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt

# P(X < 0.6) em uma exponencial de taxa 2 ou Exp(2)
prob = expon.cdf(0.6, scale=1/2)  # scale=1/taxa
print(prob)  # Output: 0.6988057880877978

# Quantil que limita 2.5% em uma Exp(2)
quantil = expon.ppf(0.025, scale=1/2)
print(quantil)  # Output: 0.012658904143650576

# Simulando 1000 valores pseudo aleatórios de uma Exp(2)
np.random.seed(999)
x = expon.rvs(size=1000, scale=1/2)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma exponencial de taxa 2, sobrepondo valores simulados
plt.hist(x, density=True, bins='auto', color='lightgray', 
         edgecolor='black')
plt.title('Exp(2)')

# Curva da densidade exponencial teórica
x_range = np.linspace(x.min(), x.max(), 100)
plt.plot(x_range, expon.pdf(x_range, scale=1/2), color='red')

plt.show()

Exemplo 3.55 Considere um pedágio onde passam em média \(\lambda = 2\) veículos por minuto. Assim, \[ X \sim \mathcal{E}(2),\] \[ f(x) = 2 e^{-2 x}, \] \[ E(X)=\frac{1}{2}=0.5, \] \[ V(X)=\frac{1}{2^2}=0.25, \] \[ D(X) = \sqrt{0.25} = 0.5. \]

Exercício 3.24 Considere os dados do Exemplo 3.55.

  1. Defina \(F(x)\).
  2. Obtenha \(P(X<1)\).
  3. Obteha \(P(X>2)\).
  4. Faça o esboço do gráfico de \(f(x)\).

Exercício 3.25 Considere a densidade da exponencial dada pela Eq. (3.77), as definições (3.68), (3.69) e (3.43).

  1. Mostre que \(F(x) = 1-e^{-\lambda x}\).
  2. Mostre que \(E(X) = \lambda^{-1}\).
  3. Mostre que \(V(X) = \lambda^{-2}\).

A distribuição exponencial também pode ser parametrizada por um parâmetro de escala \(\beta = \frac{1}{\lambda}\). Assim,

\[\begin{equation} f(x|\beta) = \frac{1}{\beta}e^{-x/\beta} \tag{3.81} \end{equation}\] \[\begin{equation} F(x|\beta) = 1 - e^{-x/\beta} \tag{3.82} \end{equation}\] A esperança e variância são dadas por \[\begin{equation} E(X)= \beta \tag{3.83} \end{equation}\] \[\begin{equation} V(X)=\beta^2 \tag{3.84} \end{equation}\]

3.9.3 Normal \(\cdot \; \mathcal{N}(\mu,\sigma)\)

A distribuição normal ou gaussiana (em homenagem a Johann Carl Friedrich Gauss) é anotada por \(\mathcal{N}(\mu,\sigma)\). Sua função densidade é dada por \[\begin{equation} f(x|\mu,\sigma) = \frac{1}{\sqrt{2\pi} \sigma} \exp \bigg\{ -\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right) ^2 \bigg\} \tag{3.85} \end{equation}\]

para \(-\infty < x < \infty\), \(-\infty < \mu < \infty\), \(\sigma > 0\). Os parâmetros \(\mu\) e \(\sigma\) podem ser calculados respectivamente pelas Equações (2.13) e (2.35). A notação \(\exp\{...\}\) representa o número de Euler elevado à expressão delimitada pelos colchetes.

A distribuição normal padrão é dada pela expressão \[\begin{equation} f(z|\mu=0, \sigma=1) = \frac{1}{\sqrt{2\pi}} \exp \bigg\{ -\frac{z^2}{2} \bigg\} \tag{3.86} \end{equation}\]

para \(-\infty < z < \infty\).

Exemplo 3.56 A distribuição normal pode ser operada com as funções stats::dnorm() (densidade), stats::pnorm() (probabilidade acumulada), stats::qnorm() (quantil) e stats::rnorm() (aleatório/random).

# P(X < 2) em uma N(0,1)
pnorm(2)
## [1] 0.9772499
# quantil que limita 2.5% em uma N(0,1)
qnorm(0.025)
## [1] -1.959964
# simulando 1000 valores pseudo aleatórios de uma N(0,1)
set.seed(999); x <- rnorm(1000)
summary(x)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -3.073370 -0.705544 -0.009566 -0.032516  0.636538  3.061137
# densidade de uma N(0,1), sobrepondo valores simulados
hist(x, freq = FALSE, main = 'N(0,1)')
curve(dnorm(x), add = TRUE, col = 'red')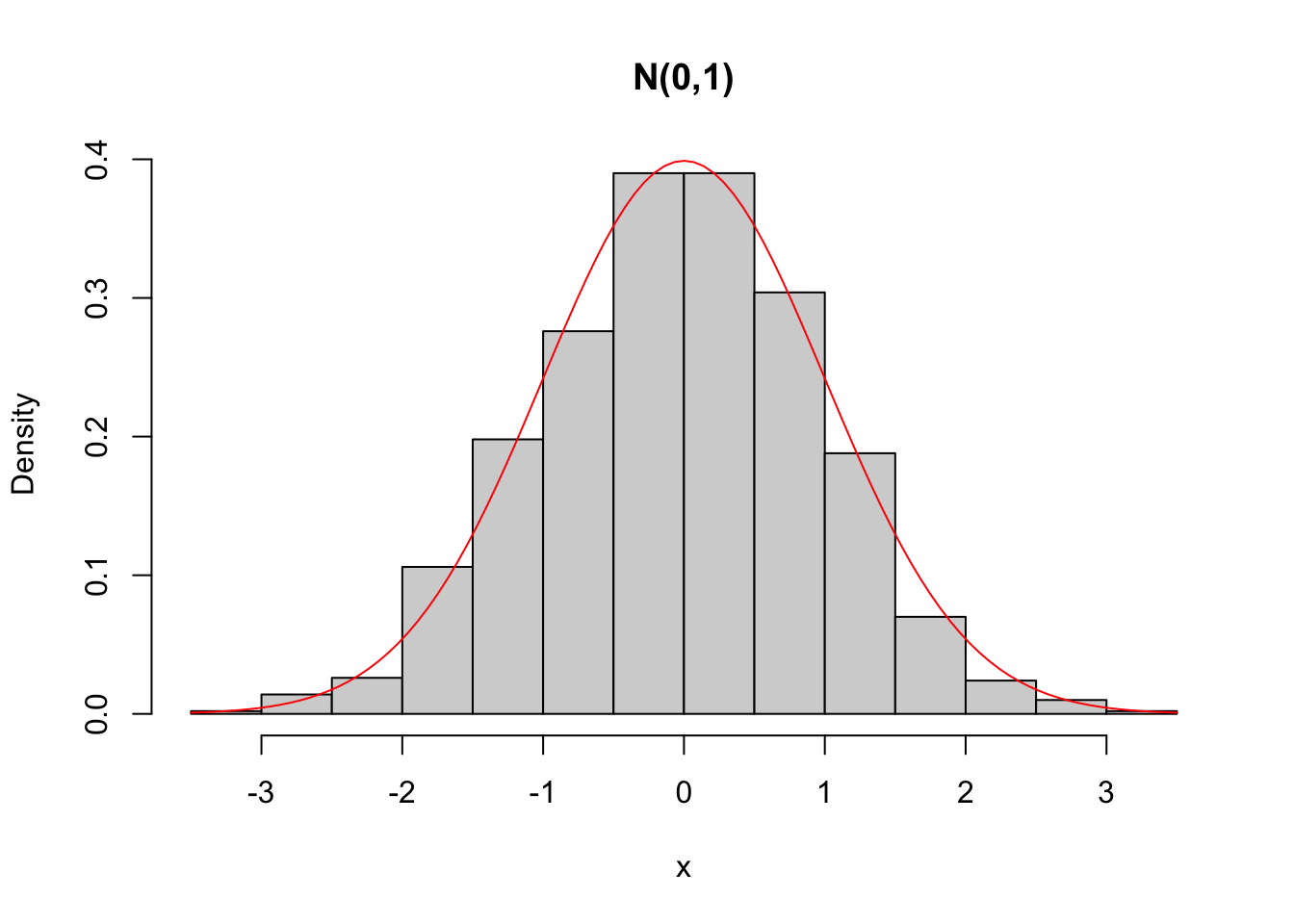

Exemplo 3.57 Em Python.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# P(X < 2) em uma N(0,1)
prob = norm.cdf(2)
print(prob)  # Output: 0.9772498680518208

# Quantil que limita 2.5% em uma N(0,1)
quantil = norm.ppf(0.025)
print(quantil)  # Output: -1.959963984540054

# Simulando 1000 valores pseudo aleatórios de uma N(0,1)
np.random.seed(999)
x = np.random.normal(size=1000)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma N(0,1), sobrepondo valores simulados
plt.hist(x, density=True, bins='auto', color='lightgray', 
         edgecolor='black')
plt.title('N(0,1)')

# Curva da densidade normal teórica
x_range = np.linspace(x.min(), x.max(), 100)
plt.plot(x_range, norm.pdf(x_range), color='red')

plt.show()

Exercício 3.26 Leia o artigo 68–95–99.7 rule.

3.9.3.1 Teorema Central do Limite

The central limit theorem says roughly that the sum of many independent random variables will be approximately normally distributed if each summand has high probability of being small. (Billingsley 1986, 366)

Teorema 3.2 (Teorema Central do Limite de Lindeberg-Lévy) Seja \(X_{1}, X_{2}, \ldots, X_{n}\) uma sequência de variáveis aleatórias independentes com \(E(X_{n}) = \mu\) e \(V(X_{n}) = \sigma^2 < \infty\). Considerando \(S_n=X_{1}+X_{2}+\ldots+X_{n}\), e se \(n \longrightarrow \infty\), então \[\begin{equation} \frac{S_n - n\mu}{\sigma \sqrt{n}} \xrightarrow{D} \mathcal{N}(0,1). \tag{3.87} \end{equation}\]

A simbologia \(\xrightarrow{D}\) indica convergência em distribuição conforme Eq. (3.118).

Notemos, então, a diferença entre o Teorema Central do Limite e a Lei dos Grandes Números [Seção 2.3.3.1] neste caso. A Lei dos Grandes Números diz que a média amostral \(S_n/n\) converge para \(\mu\), em probabilidade ou quase certamente [Seção 3.10], i.e., a diferença \(S_n/n - \mu\) tende para zero, e o Teorema Central do Limite diz que esta diferença, quando multiplicada pela raiz quadrada de \(n\), converge em distribuição para uma normal: \(\sqrt{n} \left( \frac{S_n}{n}-\mu \right) \xrightarrow{D} \mathcal{N}(0,\sigma^2).\) (James 2010, 266)

(James 2010,C) sugere o uso da expressão ‘Teorema Central do Limite’ no lugar de ‘Teorema do Limite Central’, pois central é o teorema, não o limite. A origem da expressão é atribuída ao matemático húngaro George Pólya, ao se referir a der zentrale Grenzwertsatz, i.e., o ‘central’ refere-se ao ‘teorema do limite’.

Exercício 3.27 Mostre que a Eq. (3.87) pode ser escrita em função da média \(M_n=\frac{S_n}{n}\), tal que \(\frac{M_n - \mu}{\sigma / \sqrt{n}}\).

Exercício 3.28 Assita ao vídeo But what is the Central Limit Theorem? do canal 3Blue1Brown. Agradeço ao Vitor Luiz Cavagnolli Machado pela sugestão.

3.9.3.2 Aproximando a binomial pela normal

A proporção é uma média no caso de a variável admitir apenas os valores 0 e 1, portanto o TCL se aplica diretamente a este tipo de estrutura. Pode-se ainda considerar uma correção de continuidade, somando-se 0.5 no numerador da Equação (3.87).

Exemplo 3.58 (Aproximação da binomial pela normal) Se considerarmos \(n=420\) lançamentos de uma moeda com \(p=0.5\), temos que a v.a. \(X\): ‘número de caras em 420 lançamentos’ é tal que \(X \sim \mathcal{B}(420,0.5)\). A probabilidade de obtermos até 200 caras pode ser aproximada pelo pelo TCL. \[ P(X \le 200) \approx P \left( Z < \frac{200-420\times 0.5}{\sqrt{420 \times 0.5 \times 0.5}} \right) = \Phi(-0.9759) \approx 0.164557. \] Utilizando a correção de continuidade, \[ P(X \le 200) \approx P \left( Z < \frac{200+0.5-420\times 0.5}{\sqrt{420 \times 0.5 \times 0.5}} \right) = \Phi(-0.9271) \approx 0.176936. \] Com um computador é possível calcular a probabilidade exata, perceba a proximidade dos resultados. \[ P(X \le 200) = \left[ \dbinom{420}{0} + \dbinom{420}{1} + \cdots + \dbinom{420}{200} \right] 0.5^{420} \approx 0.1769429. \]

n <- 420
p <- 0.5
S <- 200
mS <- n*p  # 210
sS <- sqrt(n*p*(1-p))  # 10.24695
# Aproximação da binomial pela normal SEM correção de continuidade
(z <- (S-mS)/sS)
## [1] -0.9759001
pnorm(z)
## [1] 0.164557
# Aproximação da binomial pela normal COM correção de continuidade
(zc <- (S+0.5-mS)/sS)
## [1] -0.9271051
pnorm(zc)
## [1] 0.176936
# Probabilidade exata
pbinom(S,n,p)
## [1] 0.1769429

Exemplo 3.59 Em Python.

import numpy as np
from scipy.stats import norm, binom

# Parâmetros da distribuição binomial
n = 420
p = 0.5
S = 200

# Média e desvio padrão da distribuição binomial
mS = n * p  # 210
sS = np.sqrt(n * p * (1 - p))  # 10.24695

# Aproximação da binomial pela normal SEM correção de continuidade
z = (S - mS) / sS
prob_sem_correcao = norm.cdf(z)
print(prob_sem_correcao)  # Output: 0.1668580917315335

# Aproximação da binomial pela normal COM correção de continuidade
zc = (S + 0.5 - mS) / sS
prob_com_correcao = norm.cdf(zc)
print(prob_com_correcao)  # Output: 0.1715144436436775

# Probabilidade exata
prob_exata = binom.cdf(S, n, p)
print(prob_exata)  # Output: 0.1713874634776793

3.9.3.3 Para saber mais

(Patel and Read 1982) trazem uma coleção de resultados e propriedades relacionados à distribuição normal. (Tong 1990) fornece um tratamento abrangente de resultados relacionados à distribuição normal multivariada. Os temas principais são dependência, desigualdades de probabilidade e seus papéis na teoria e aplicações.

3.9.4 Qui-quadrado \(\cdot \; \mathcal{\chi}^2(\nu)\)

A variável aleatória contínua \(X\) tem distribuição qui-quadrado com \(\nu\) graus de liberdade, anotada por \(X \sim \chi^2(\nu)\), se sua função densidade é dada por

\[\begin{equation} f(x|\nu) = \frac{1}{\Gamma \left( \frac{\nu}{2} \right) 2^{\nu/2}} x^{\frac{\nu}{2}-1} e^{-\frac{x}{2}} \tag{3.88} \end{equation}\]

onde \(x > 0\), \(\nu > 0\) e \(\Gamma\) indica a função gama tal que

\[\begin{equation} \Gamma(x) = \int_{0}^{\infty} t^{x-1} e^{-t} dt \tag{3.89} \end{equation}\]

Exemplo 3.60 A distribuição \(\chi^2\) pode ser operada com as funções stats::dchisq() (densidade), stats::pchisq() (probabilidade acumulada), stats::qchisq() (quantil) e stats::rchisq() (aleatório/random).

# P(X < 2) em uma \chi^2 com 1 gl
gl <- 1
pchisq(2, gl)
## [1] 0.8427008
# quantil que limita 2.5% em uma \chi^2 com 1 gl
qchisq(0.025, gl)
## [1] 0.0009820691
# simulando 1000 valores pseudo aleatórios de uma \chi^2 com 1 gl
set.seed(135); x <- rchisq(1000, gl)
summary(x)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000002 0.0863372 0.4272770 0.9860635 1.3076778 8.9145053
# densidade de uma \chi^2 com 1 gl, sobrepondo valores simulados
hist(x, 50, freq = FALSE, main = bquote(chi^2~  (.(gl))))
curve(dchisq(x,1), 0, 10, add = TRUE, col = 'red')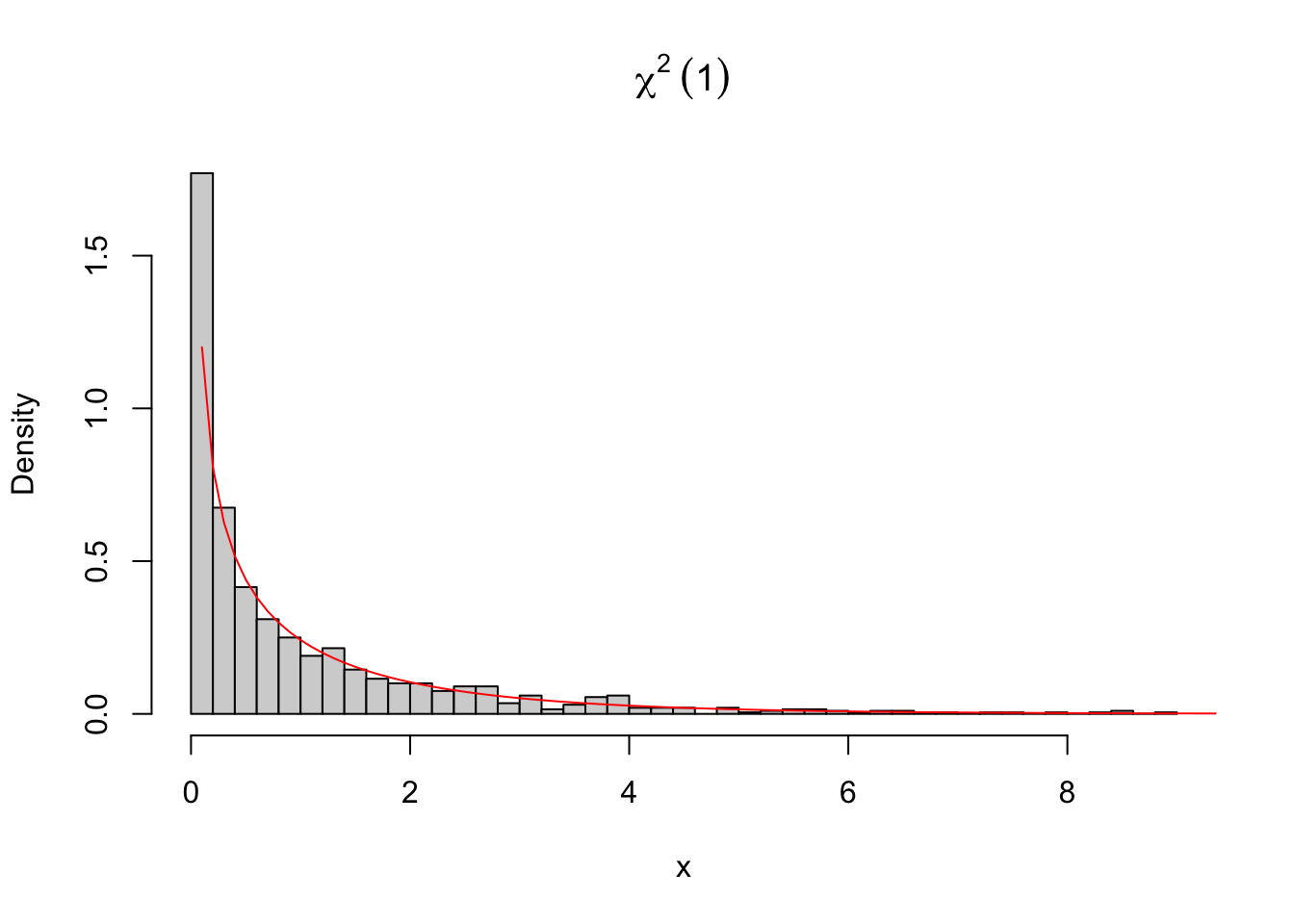

Exemplo 3.61 Em Python.

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt

# P(X < 2) em uma chi^2 com 1 gl
gl = 1
prob = chi2.cdf(2, df=gl)
print(prob)  # Output: 0.8427007929497149

# Quantil que limita 2.5% em uma chi^2 com 1 gl
quantil = chi2.ppf(0.025, df=gl)
print(quantil)  # Output: 0.0009820691171752559

# Simulando 1000 valores pseudo aleatórios de uma chi^2 com 1 gl
np.random.seed(135)
x = chi2.rvs(size=1000, df=gl)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma chi^2 com 1 gl, sobrepondo valores simulados
plt.hist(x, density=True, bins=50, color='lightgray', 
         edgecolor='black')
# Usando LaTeX para o título
plt.title(r'$\chi^2$(' + str(gl) + ')', fontsize=16)

# Curva da densidade chi^2 teórica
x_range = np.linspace(0, 10, 500)
plt.plot(x_range, chi2.pdf(x_range, df=gl), color='red')

plt.show()

3.9.4.1 Caracterização

De acordo com (Johnson, Kotz, and Balakrishnan 1994, 416–17),

\[\begin{equation} \chi^2(\nu) = \sum_{i=1}^\nu Z_i^2 \tag{3.90} \end{equation}\]

onde \(Z_i^2 \sim \mathcal{N}(0,1)\), \(i \in \{1,\ldots,\nu\}\).

Exemplo 3.62 É possível simular uma qui-quadrado com 1 grau de liberdade.

# via normal padrão ao quadrado
set.seed(1234); q1 <- rnorm(1000)^2
# via base::rchisq
set.seed(5678); q2 <- rchisq(1000,1)
par(mfrow=c(1,2))
h1 <- hist(q1, 30, freq = FALSE, main = 'Via N(0,1)^2')
curve(dchisq(x, 1), range(h1$breaks), add = TRUE, col = 'red')
h2 <- hist(q2, 30, freq = FALSE, main = 'Via stats::rchisq()')
curve(dchisq(x, 1), range(h2$breaks), add = TRUE, col = 'red')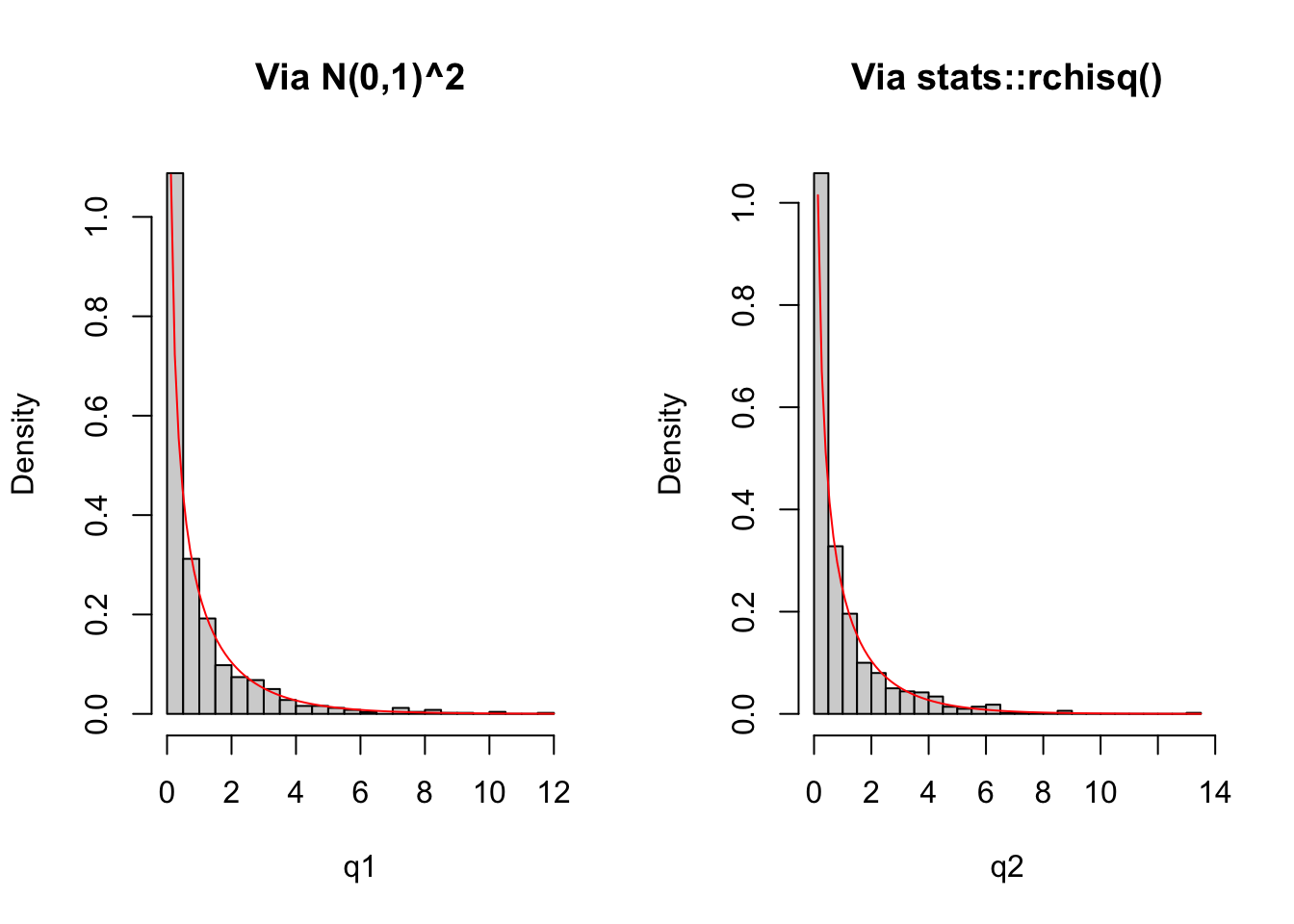

# verificando a aderência das simulações
ks.test(q1, q2)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  q1 and q2
## D = 0.026, p-value = 0.8879
## alternative hypothesis: two-sided

Exemplo 3.63 Em Python.

import numpy as np
from scipy.stats import norm, chi2, ks_2samp
import matplotlib.pyplot as plt

# Via normal padrão ao quadrado
np.random.seed(1234)
q1 = norm.rvs(size=1000)**2

# Via scipy.stats.chi2
np.random.seed(5678)
q2 = chi2.rvs(size=1000, df=1)

# Histogramas
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# Histograma de q1
axs[0].hist(q1, bins=30, density=True, color='lightgray', 
            edgecolor='black')
axs[0].set_title('Via normal padrão ao quadrado')
x_range = np.linspace(q1.min(), q1.max(), 100)
axs[0].plot(x_range, chi2.pdf(x_range, df=1), color='red')

# Histograma de q2
axs[1].hist(q2, bins=30, density=True, color='lightgray', 
            edgecolor='black')
axs[1].set_title('Via scipy.stats.chi2')
x_range = np.linspace(q2.min(), q2.max(), 100)
axs[1].plot(x_range, chi2.pdf(x_range, df=1), color='red')

plt.show()

# Teste de Kolmogorov-Smirnov
ks_statistic, p_value = ks_2samp(q1, q2)
print(f"Estatística KS: {ks_statistic:.4f}")
print(f"Valor-p: {p_value:.4f}")

Exercício 3.29 Simule uma qui-quadrado com 3 graus de liberdadade via Eq. (3.90). Compare com a simulação obtida via stats::rchisq().

3.9.5 \(t\) de Student \(\cdot \; \mathcal{t(\nu)}\)

A variável aleatória contínua \(X\) tem distribuição \(t\) de Student com \(\nu\) graus de liberdade, anotada por \(X \sim t(\nu)\), se sua função densidade é dada por

\[\begin{equation} f(x|\nu) = \frac{\Gamma \left( \frac{\nu+1}{2} \right)}{\Gamma \left( \frac{\nu}{2} \right) \sqrt{\nu \pi}} \left( 1+\frac{x^2}{\nu} \right)^{-\frac{\nu + 1}{2}} \tag{3.91} \end{equation}\]

onde \(-\infty < x < \infty\), \(\nu > 0\) e \(\Gamma\) indica a conforme Eq. (3.89).

Exemplo 3.64 A distribuição \(t\) pode ser operada com as funções stats::dt() (densidade), stats::pt() (probabilidade acumulada), stats::qt() (quantil) e stats::rt() (aleatório/random).

# P(X < 2) em uma t com 1 gl
pt(2, 1)
## [1] 0.8524164
# quantil que limita 2.5% em uma t com 1 gl
qt(0.025, 1)
## [1] -12.7062
# simulando 1000 valores pseudo aleatórios de uma t com 1 gl
set.seed(246); x <- rt(1000, 1)
summary(x)
##       Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
## -305.19517   -1.13355   -0.08911    0.34201    1.04303 1294.51346
# densidade de uma t com 1 gl, sobrepondo valores simulados
hist(x, 3000, freq = FALSE, xlim = c(-15,15), 
     main = expression(italic('t')[1]))
curve(dt(x,1), add = TRUE, col = 'red')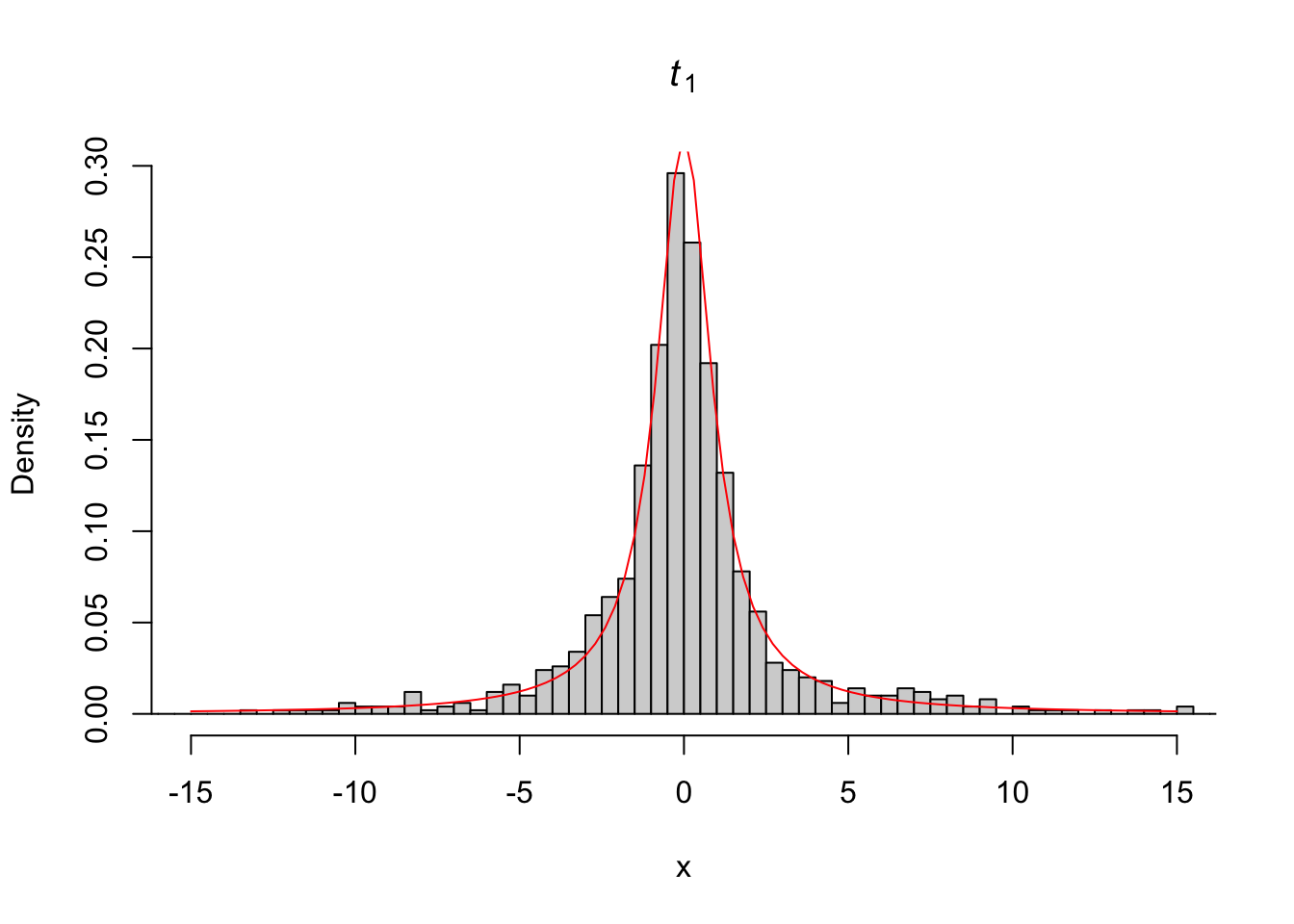

Exemplo 3.65 Em Python.

import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt

# Pr(X < 2) em uma t com 1 gl
prob = t.cdf(2, df=1)
print(prob)  # Output: 0.8524163823517757

# Quantil que limita 2.5% em uma t com 1 gl
quantil = t.ppf(0.025, df=1)
print(quantil)  # Output: -12.706204736174703

# Simulando 1000 valores pseudo aleatórios de uma t com 1 gl
np.random.seed(246)
x = t.rvs(size=1000, df=1)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma t com 1 gl, sobrepondo valores simulados
plt.hist(x, density=True, bins=3000, color='lightgray', 
         edgecolor='black')
plt.xlim(-15, 15)  # Definindo o limite do eixo x
# Usando expressão matemática LaTeX para o título
plt.title(r'$t(1)$', fontsize=16)

# Curva da densidade t teórica
x_range = np.linspace(-15, 15, 1000)
plt.plot(x_range, t.pdf(x_range, df=1), color='red')

plt.show()

3.9.5.1 Caracterização

De acordo com (Johnson, Kotz, and Balakrishnan 1995, 362),

\[\begin{equation} t(\nu) = Z \left[ \frac{\chi^2(\nu)}{\nu} \right]^{-1/2} \tag{3.92} \end{equation}\]

onde \(Z \sim \mathcal{N}(0,1)\).

3.9.6 Fisher-Snedecor \(\cdot \; \mathcal{F}(\nu_1,\nu_2)\)

Se \(X \sim \mathcal{F}(\nu_1,\nu_2)\), então sua função densidade é dada por

\[\begin{equation} f(x|\nu_1,\nu_2) = \frac{\sqrt{\frac{(\nu_1 x)^{\nu_1} \nu_2^{\nu_2}}{(\nu_1 x+\nu_2)^{\nu_1 + \nu_2}}}}{x B\left( \frac{\nu_1}{2}, \frac{\nu_2}{2} \right)} \tag{3.93} \end{equation}\]

onde \(x > 0\), \(\nu_1 > 0\) indica os graus de liberdade do numerador, \(\nu_2 > 0\) indica os graus de liberdade do denominador e \(B\) indica a função beta, tal que

\[\begin{equation} B(x_1,x_2) = \int_{0}^{1} t^{x_1 - 1} (1-t)^{x_2 - 1} dt = \frac{\Gamma(x_1) \Gamma(x_2)}{\Gamma(x_1+x_2)} \tag{3.94} \end{equation}\]

Exemplo 3.66 A distribuição \(\mathcal{F}\) pode ser operada com as funções stats::df() (densidade), stats::pf() (probabilidade acumulada), stats::qf() (quantil) e stats::rf() (aleatório/random).

# P(X < 2) em uma F com 1 gl do numerador e 3 gl do denominador
gl1 <- 1
gl2 <- 3
pf(2, gl1, gl2)
## [1] 0.7477845
# quantil que limita 2.5% em uma F(1,3)
qf(0.025, gl1, gl2)
## [1] 0.001157189
# simulando 1000 valores pseudo aleatórios de uma F(1,3)
set.seed(1010); x <- rf(1000, gl1, gl2)
summary(x)
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##   0.0000   0.1073   0.5564   2.3601   1.9758 120.0880
# densidade de uma F(1,3), sobrepondo valores simulados
hist(x, 500, freq = FALSE, xlim = c(0,10), 
     main = bquote(F(.(gl1),.(gl2))))
curve(df(x, gl1, gl2), 0, 10, add = TRUE, col = 'red')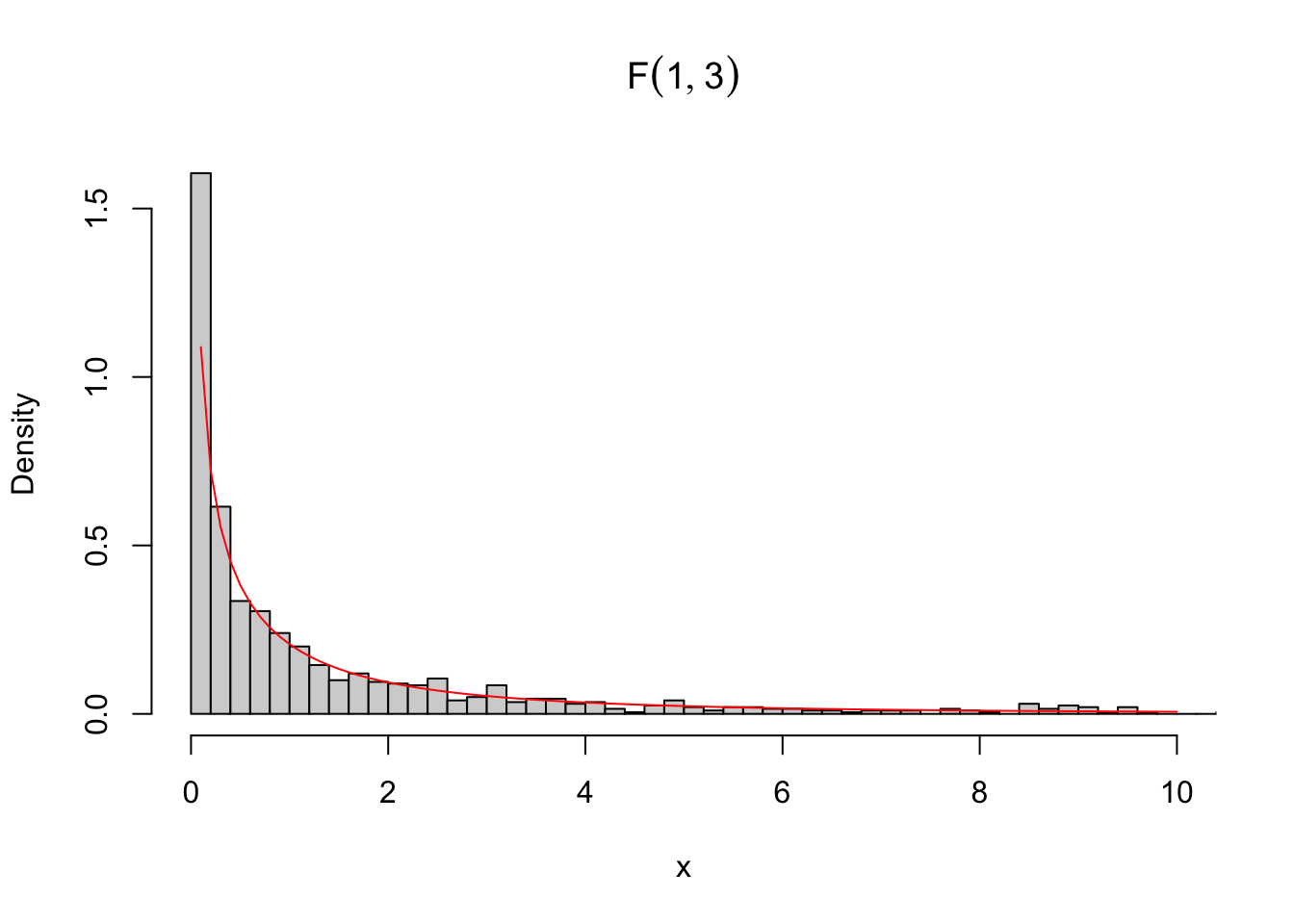

Exemplo 3.67 Em Python.

import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt

# P(X < 2) em uma F com 1 gl do numerador e 3 gl do denominador
gl1 = 1
gl2 = 3
prob = f.cdf(2, dfn=gl1, dfd=gl2)
print(prob)  # Output: 0.7205735894497143

# Quantil que limita 2.5% em uma F(1,3)
quantil = f.ppf(0.025, dfn=gl1, dfd=gl2)
print(quantil)  # Output: 0.07173676809618983

# Simulando 1000 valores pseudo aleatórios de uma F(1,3)
np.random.seed(1010)
x = f.rvs(size=1000, dfn=gl1, dfd=gl2)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma F(1,3), sobrepondo valores simulados
plt.hist(x, density=True, bins=500, color='lightgray', 
         edgecolor='black')
plt.xlim(0, 10)  # Definindo o limite do eixo x
# Usando LaTeX para o título
plt.title(r'$F$(' + str(gl1) + ',' + str(gl2) + ')', fontsize=16)

# Curva da densidade F teórica
x_range = np.linspace(0, 10, 500)
plt.plot(x_range, f.pdf(x_range, dfn=gl1, dfd=gl2), color='red')

plt.show()

3.9.6.1 Caracterização

De acordo com (Johnson, Kotz, and Balakrishnan 1995, 322),

\[\begin{equation} \mathcal{F}(\nu_1,\nu_2) = \frac{\chi^2(\nu_1)/\nu_1}{\chi^2(\nu_2)/\nu_2} \tag{3.95} \end{equation}\]

Exemplo 3.68 É possível simular uma \(\mathcal{F}\) com \(\nu_1=1\) grau de liberdade no numerador e \(\nu_2=3\) graus de liberdade no denominador.

set.seed(1234); q1 <- rchisq(1000, 1)
set.seed(5678); q2 <- rchisq(1000, 3)
x1 <- (q1/1)/(q2/3)
x2 <- rf(1000, 1, 3)
par(mfrow=c(1,2))
hist(x1, 50, freq = FALSE, xlim = c(0,20))
curve(df(x,1,3), 0, 20, add = TRUE, col = 'red')
hist(x2, 100, freq = FALSE, xlim = c(0,20))
curve(df(x,1,3), 0, 20, add = TRUE, col = 'red')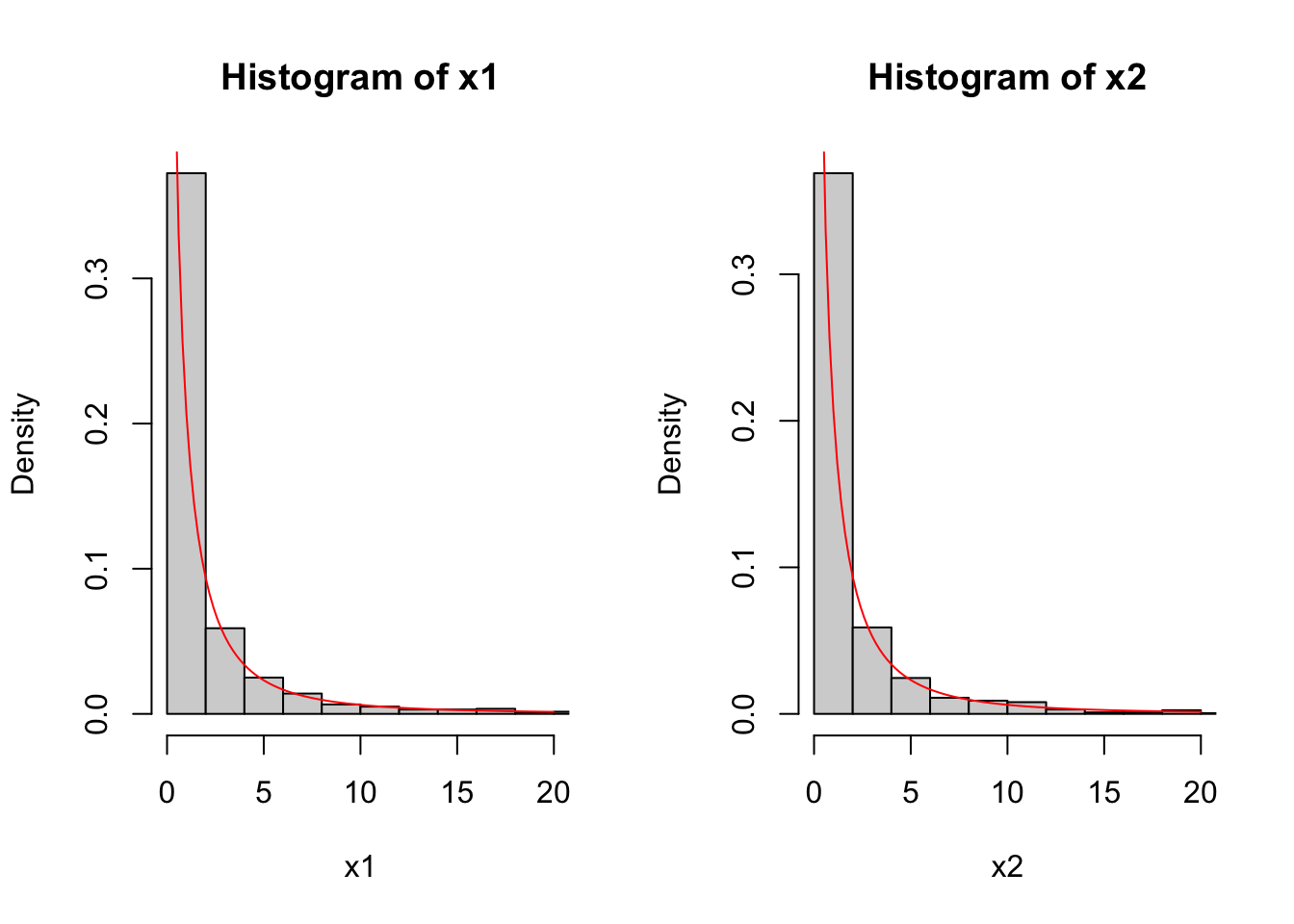

ks.test(x1, x2)
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  x1 and x2
## D = 0.023, p-value = 0.9541
## alternative hypothesis: two-sided

Exemplo 3.69 Em Python.

import numpy as np
from scipy.stats import chi2, f, ks_2samp
import matplotlib.pyplot as plt

# Gerando valores de distribuições qui-quadrado
np.random.seed(1234)
q1 = chi2.rvs(size=1000, df=1)
np.random.seed(5678)
q2 = chi2.rvs(size=1000, df=3)

# Calculando x1 e x2
x1 = (q1 / 1) / (q2 / 3)
x2 = f.rvs(size=1000, dfn=1, dfd=3)

# Histogramas
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# Histograma de x1
axs[0].hist(x1, bins=50, density=True, color='lightgray', 
            edgecolor='black')
axs[0].set_xlim(0, 20)
axs[0].set_title('(q1/1) / (q2/3)')
x_range = np.linspace(0, 20, 500)
axs[0].plot(x_range, f.pdf(x_range, dfn=1, dfd=3), color='red')

# Histograma de x2
axs[1].hist(x2, bins=100, density=True, color='lightgray', 
            edgecolor='black')
axs[1].set_xlim(0, 20)
axs[1].set_title('f.rvs(1000, 1, 3)')
x_range = np.linspace(0, 20, 500)
axs[1].plot(x_range, f.pdf(x_range, dfn=1, dfd=3), color='red')

plt.show()

# Teste de Kolmogorov-Smirnov
ks_statistic, p_value = ks_2samp(x1, x2)
print(f"Estatística KS: {ks_statistic:.4f}")
print(f"Valor-p: {p_value:.4f}")

3.9.7 Beta \(\cdot \; \mathcal{Beta}(\alpha,\beta)\)

A função densidade beta é dada por \[\begin{equation} f(x|\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1} (1-x)^{\beta-1} \tag{3.96} \end{equation}\] onde \(0 \le x \le 1\), \(\alpha,\beta > 0\) e \(\Gamma\) é a função gama conforme Eq. (3.89). A esperança e variância são dadas por \[\begin{equation} E(X) = \frac{\alpha}{\alpha+\beta} \tag{3.97} \end{equation}\] \[\begin{equation} V(X) = \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \tag{3.98} \end{equation}\]

A mediana e moda são dadas por \[\begin{equation} Md(X) \approx \frac{\alpha-1/3}{\alpha+\beta-2/3} \tag{3.99} \end{equation}\] \[\begin{equation} Mo(X) = \frac{\alpha-1}{\alpha+\beta-2}, \; \alpha,\beta>1 \tag{3.100} \end{equation}\] \[\begin{equation} Mo(X) \; \text{algum valor entre 0 e 1}, \; \alpha=\beta=1 \tag{3.101} \end{equation}\] \[\begin{equation} Mo(X) = \{0,1\}, \; \alpha,\beta<1 \tag{3.102} \end{equation}\] \[\begin{equation} Mo(X) = 0, \; \alpha \le 1,\beta>1 \tag{3.103} \end{equation}\] \[\begin{equation} Mo(X) = 1, \; \alpha>1,\beta \le 1 \tag{3.104} \end{equation}\]

Exemplo 3.70 A distribuição Beta pode ser operada com as funções stats::dbeta() (densidade), stats::pbeta() (probabilidade acumulada), stats::qbeta() (quantil) e stats::rbeta() (aleatório/random).

# P(X < 0.5) em uma Beta(1,3)
pbeta(0.5, 1, 3)
## [1] 0.875
# quantil que limita 2.5% em uma Beta(1,3)
qbeta(0.025, 1, 3)
## [1] 0.008403759
# simulando 1000 valores pseudo aleatórios de uma Beta(1,3)
set.seed(1010); x <- rbeta(1000, 1, 3)
summary(x)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 8.425e-05 9.054e-02 2.127e-01 2.502e-01 3.621e-01 9.394e-01
# densidade de uma Beta(1,3), sobrepondo valores simulados
hist(x, 30, freq = FALSE, ylim = c(0, 3), main = 'Beta(1,3)')
curve(dbeta(x,1,3), add = TRUE, col = 'red')

Exemplo 3.71 Em Python.

import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

# P(X < 1/2) em uma Beta(1,3)
prob = beta.cdf(1/2, a=1, b=3)
print(prob)  # Output: 0.875

# Quantil que limita 2.5% em uma Beta(1,3)
quantil = beta.ppf(0.025, a=1, b=3)
print(quantil)  # Output: 0.04466154539950399

# Simulando 1000 valores pseudo aleatórios de uma Beta(1,3)
np.random.seed(1010)
x = beta.rvs(size=1000, a=1, b=3)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma Beta(1,3), sobrepondo valores simulados
plt.hist(x, density=True, bins=30, color='lightgray', 
         edgecolor='black')
plt.ylim(0, 3)  # Definindo o limite do eixo y
plt.title('Beta(1,3)')

# Curva da densidade Beta teórica
x_range = np.linspace(0, 1, 100)
plt.plot(x_range, beta.pdf(x_range, a=1, b=3), color='red')

plt.show()

3.9.8 Gama \(\cdot \; \mathcal{Gama}(k,g)\)

A função densidade gama pode ser dada por \[\begin{equation} f(x|k,g) = \frac{1}{\Gamma(k) g^k} x^{k-1} e^{-\frac{x}{g}} \tag{3.105} \end{equation}\] onde \(x>0\), \(k>0\) (forma/shape), \(g>0\) (escala/scale) e \(\Gamma\) é a função gama conforme Eq. (3.89). A esperança e variância são dadas por \[\begin{equation} E(X) = kg \tag{3.106} \end{equation}\] \[\begin{equation} V(X) = kg^2 \tag{3.107} \end{equation}\]

A mediana não tem forma fechada, e a moda é dada por \[\begin{equation} Mo(X) = (k-1)g, \;\; k \ge 1 \tag{3.108} \end{equation}\] \[\begin{equation} Mo(X) = 0, \;\; k < 1 \tag{3.109} \end{equation}\]

Exemplo 3.72 A distribuição Gama pode ser operada com as funções stats::dgamma() (densidade), stats::pgamma() (probabilidade acumulada), stats::qgamma() (quantil) e stats::rgamma() (aleatório/random).

# P(X < 2) em uma Gama(1,3)
pgamma(2, 1, 3)
## [1] 0.9975212
# quantil que limita 2.5% em uma Gama(1,3)
qgamma(0.025, 1, 3)
## [1] 0.008439269
# simulando 1000 valores pseudo aleatórios de uma Gama(1,3)
set.seed(1010); x <- rgamma(1000, 1, 3)
summary(x)
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0003625 0.0914895 0.2279837 0.3381387 0.4639010 2.6271045
# densidade de uma Gama(1,3), sobrepondo valores simulados
hist(x, 30, freq = F, ylim = c(0, 3), main = 'Gama(1,3)')
curve(dgamma(x,1,3), add = T, col = 'red')

Exemplo 3.73 Em Python.

import numpy as np
from scipy.stats import gamma
import matplotlib.pyplot as plt

# P(X < 2) em uma Gama(1,3)
prob = gamma.cdf(2, a=1, scale=1/3)  # scale é o inverso da taxa
print(prob)  # Output: 0.950212931632136

# Quantil que limita 2.5% em uma Gama(1,3)
quantil = gamma.ppf(0.025, a=1, scale=1/3)
print(quantil)  # Output: 0.008264462809917356

# Simulando 1000 valores pseudo aleatórios de uma Gama(1,3)
np.random.seed(1010)
x = gamma.rvs(size=1000, a=1, scale=1/3)
# Resumo estatístico similar ao summary() em R via Pandas
print(pd.Series(x).describe())

# Densidade de uma Gama(1,3), sobrepondo valores simulados
plt.hist(x, density=True, bins=30, color='lightgray', 
         edgecolor='black')
plt.ylim(0, 3)  # Definindo o limite do eixo y
plt.title('Gama(1,3)')

# Curva da densidade Gama teórica
x_range = np.linspace(0, x.max(), 100)
plt.plot(x_range, gamma.pdf(x_range, a=1, scale=1/3), color='red')

plt.show()

Exercício 3.30 Considere a seguinte parametrização da distribuição Gama: \[\begin{equation} f(x|\alpha,\beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x} \tag{3.110} \end{equation}\] onde \(x>0\), \(\alpha>0\) (forma/shape) e \(\beta>0\) (taxa/rate).

  1. Verifique que o parâmetro de forma \(k\) da Eq. (3.105) é igual ao parâmetro de forma \(\alpha\) da Eq. (3.110).
  2. Verifique que o parâmetro de escala \(g\) da Eq. (3.105) é o inverso da taxa \(\beta\) da Eq. (3.110).

3.9.9 Triangular \(\cdot \; \mathcal{Tri}(a,m,b)\)

(Samuel Kotz and Van Dorp 2004, 5) definem a função densidade triangular no intervalo \([a,b]\) com moda \(m\) por \[\begin{equation} f(x|a,b,m) = \left\{ \begin{array}{l} \frac{2(x-a)}{(b-a)(m-a)}, \;\; a \le x \le m \\ \frac{2(b-x)}{(b-a)(b-m)}, \;\; m < x \le b \\ \end{array} \right. \tag{3.111} \end{equation}\]

onde \(a \le x \le b\) e \(a \le m \le b\), \(-\infty < a,b < \infty\) com \(b>a\).

Ainda de acordo com (Samuel Kotz and Van Dorp 2004, 7), sua função distribuição acumulada é26 \[\begin{equation} F(x|a,b,m) = \left\{ \begin{array}{l} \frac{(x-a)^2}{(b-a)(m-a)}, \;\; a \le x \le m \\ 1 - \frac{(b-x)^2}{(b-a)(b-m)}, \;\; m < x \le b \\ \end{array} \right. \tag{3.112} \end{equation}\]

(Samuel Kotz and Van Dorp 2004, 8) indicam a função distribuição acumulada inversa por \[\begin{equation} F^{-1}(u|a,b,m) = \left\{ \begin{array}{l} a + \sqrt{u(b-a)(m-a)}, \;\; 0 \le u \le \frac{m-a}{b-a} \\ b - \sqrt{(1-u)(b-a)(b-m)}, \;\; \frac{m-a}{b-a} < u \le 1 \\ \end{array} \right. \tag{3.113} \end{equation}\]

(Millard 2013) apresenta o pacote EnvStats, que possui funções variadas para Estatística Ambiental que contemplam a distribuição triangular, bem como (Wolodzko 2023).

library(extraDistr)
set.seed(42)
hist(rtriang(10000, a=0, b=1, c=0.5), 40, 
     freq = FALSE, main = 'Tri(0,0.5,1)')
curve(dtriang(x, a=0, b=1, c=0.5), col = 'red', add = TRUE)

Exemplo 3.74 Em Python.

import numpy as np
from scipy.stats import triang
import matplotlib.pyplot as plt

# Gerando 10000 valores de uma distribuição triangular
np.random.seed(2)
x = triang.rvs(loc=0, c=0.5, scale=1, size=10000) # c: parâmetro de forma

# Histograma
plt.hist(x, bins=40, density=True, color='lightgray', 
         edgecolor='black')
plt.title('Tri(0, 0.5, 1)')

# Curva da densidade triangular teórica
x_range = np.linspace(x.min(), x.max(), 100)
plt.plot(x_range, triang.pdf(x_range, loc=0, c=0.5, scale=1), 
         color='red')
plt.show()

Exercício 3.31 Veja as documentações de extraDistr::dtriangular() e triang.pdf().

3.9.10 Gompertz \(\cdot \; \mathcal{Gompertz}(\alpha,\beta)\)

(Gompertz 1825) define a função densidade de Gompertz de parâmetro de forma \(\alpha>0\) e de escala \(\beta>0\) para \(x>0\) por \[\begin{equation} f(x|\alpha,\beta) = \alpha \beta \exp \left\{ \beta x + \alpha - \alpha e^{\beta x} \right\} \tag{3.114} \end{equation}\]

Sua função distribuição acumulada é dada por \[\begin{equation} F(x|\alpha,\beta) = 1 - \exp \left\{ - \alpha(e^{\beta x}-1) \right\} \tag{3.115} \end{equation}\]

(Yee 2010) e (Wolodzko 2023) apresentam funções para a distribuição Gompertz. 

library(VGAM)
curve(VGAM::dgompertz(x, scale = 1, shape = .1), xlim = c(0,5), 
      ylim = c(0,1.2), col = 'red', ylab = 'VGAM::dgompertz')
curve(VGAM::dgompertz(x, scale = 1, shape = 2), xlim = c(0,5), 
      ylim = c(0,1.2), col = 'black', add = TRUE)
curve(VGAM::dgompertz(x, scale = 1, shape = 3), xlim = c(0,5), 
      ylim = c(0,1.2), col = 'blue', add = TRUE)
curve(VGAM::dgompertz(x, scale = 2, shape = 1), xlim = c(0,5), 
      ylim = c(0,1.2), col = 'green', add = TRUE)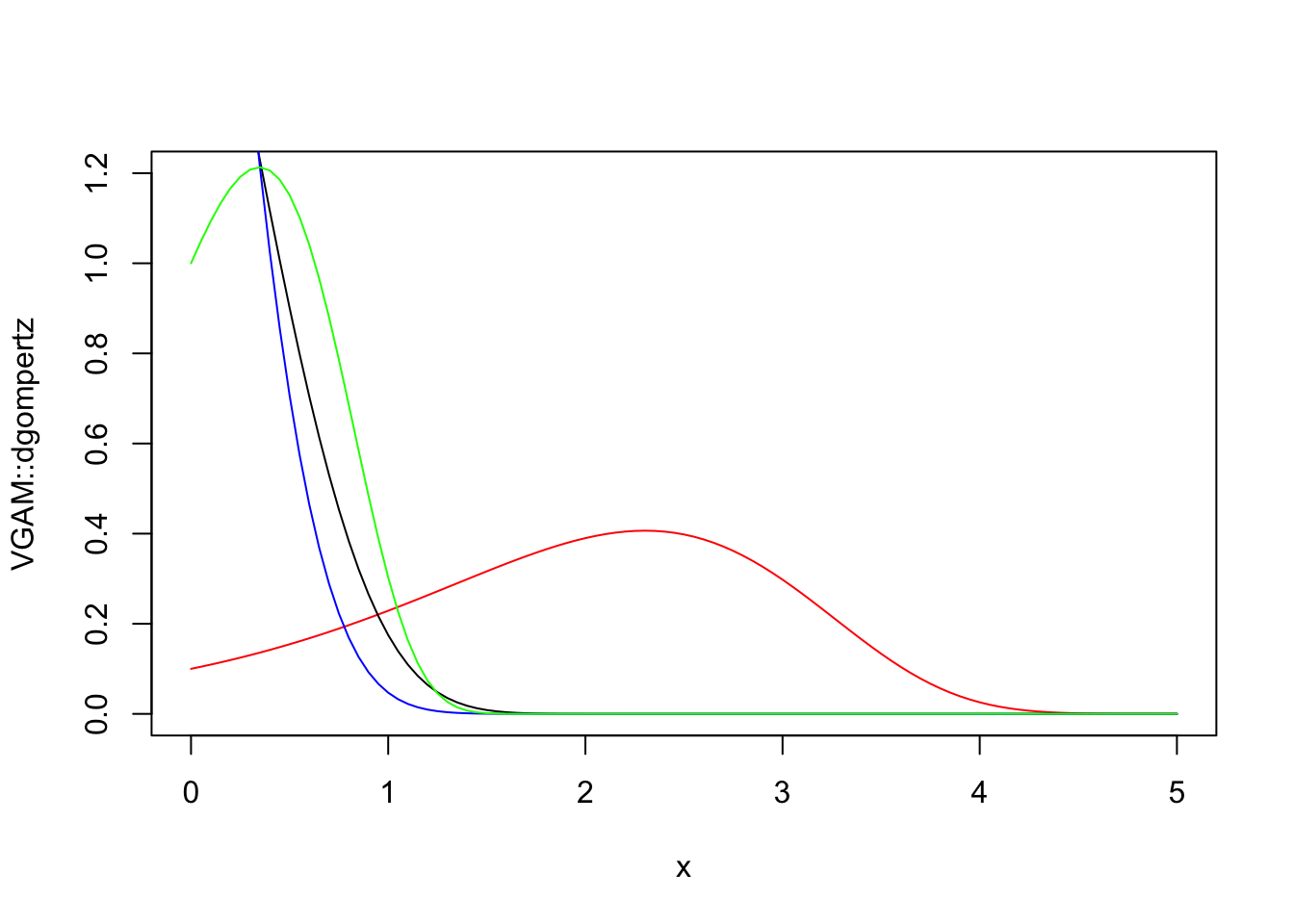

Exemplo 3.75 Em Python.

import numpy as np
from scipy.stats import gompertz
import matplotlib.pyplot as plt

# Valores de x
x = np.linspace(0, 5, 500)

# Curvas da distribuição Gompertz
plt.plot(x, gompertz.pdf(x, c=0.1), color='red',
         label='scale=1, shape=0.1')
plt.plot(x, gompertz.pdf(x, c=2), color='black', 
         label='scale=1, shape=2')
plt.plot(x, gompertz.pdf(x, c=3), color='blue', 
         label='scale=1, shape=3')
plt.plot(x, gompertz.pdf(x, c=1, scale=2), color='green', 
         label='scale=2, shape=1')

# Configurações do gráfico
plt.xlim(0, 5)
plt.ylim(0, 1.2)
plt.xlabel('x')
plt.ylabel('Densidade')
plt.title('Distribuição Gompertz')
plt.legend()

plt.show()

Exercício 3.32 Verifique a documentação de extraDistr::dgompertz() e verifique a parametrização de f e F considerando parâmetros de escala e locação.

3.9.11 Gompertz unitária \(\cdot \; \mathcal{GU}(\alpha,\beta)\)

(Mazucheli, Menezes, and Dey 2019) definem a distribuição de Gompertz unitária a partir da transformação do tipo \[X=e^{-Y}\]

onde \(Y\) tem distribuição de Gompertz. Sua função densidade de parâmetro de forma \(\alpha>0\) e de escala \(\beta>0\) para \(0<x<1\) por \[\begin{equation} f(x|\alpha,\beta) = \alpha \beta x^{-(\beta+1)} \exp \left\{ -\alpha(x^{-\beta}-1) \right\} \tag{3.116} \end{equation}\]

Sua função distribuição acumulada é dada por \[\begin{equation} F(x|\alpha,\beta) = \exp \left\{ -\alpha(x^{-\beta}-1) \right\} \tag{3.117} \end{equation}\]

(Menezes and Mazucheli 2021) apresentam o pacote unitquantreg, que fornece uma coleção de modelos de regressão quantílica paramétrica para dados delimitados. Os autores também apresentam funções para a distribuição unitária de Gompertz reparametrizada em termos do \(\tau\)-ésimo quantil, \(\tau \in (0,1)\).

library(unitquantreg)
set.seed(123)
x <- rugompertz(n = 5000, mu = 0.5, theta = 2, tau = 0.5)
R <- range(x)
S <- seq(from = R[1], to = R[2], by =  0.01)
hist(x, prob = TRUE, main = 'Gompertz unitária')
lines(S, dugompertz(x = S, mu = 0.5, theta = 2, tau = 0.5), col=2)

plot(ecdf(x))
lines(S, pugompertz(q = S, mu = 0.5, theta = 2, tau = 0.5), col=2)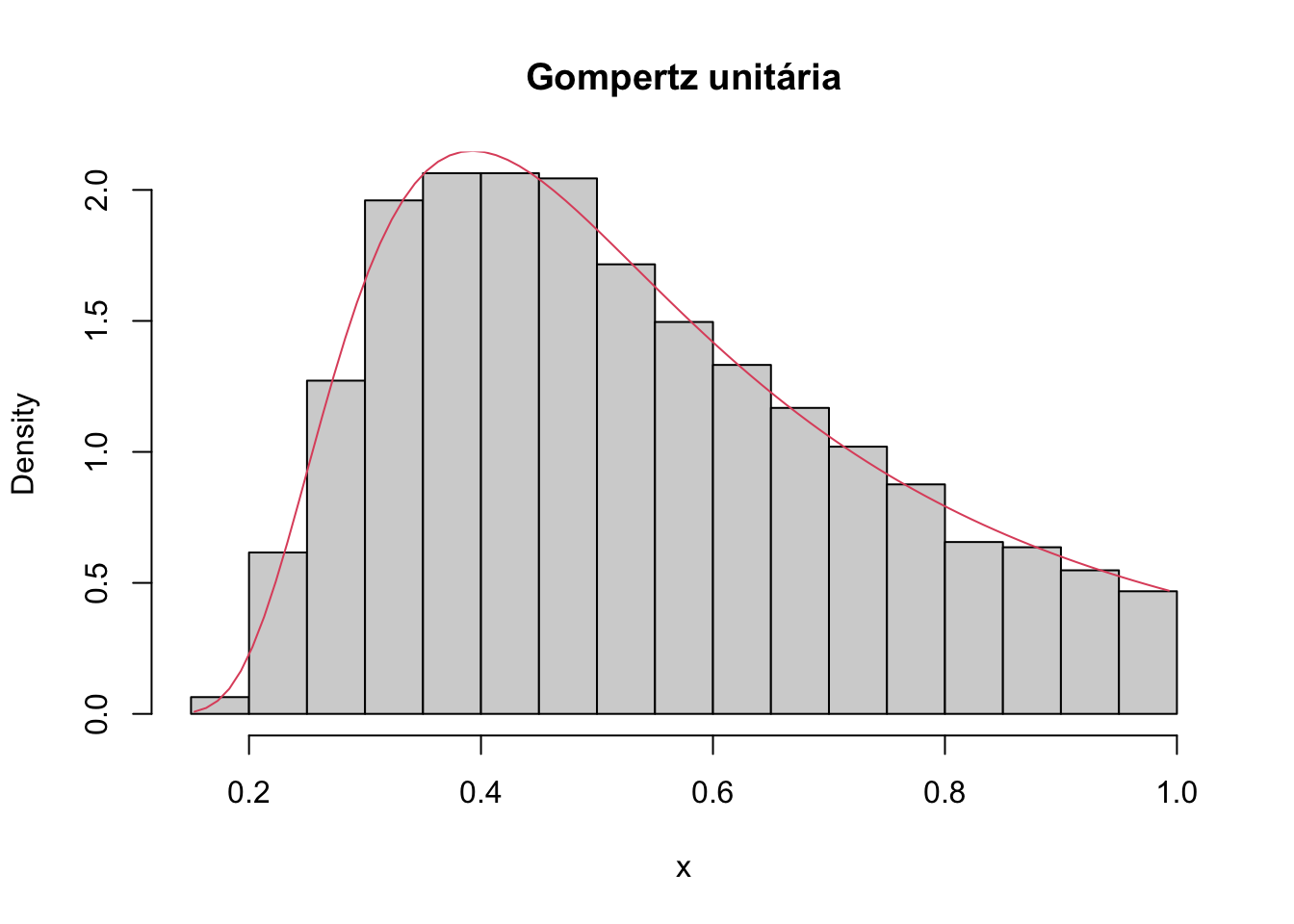

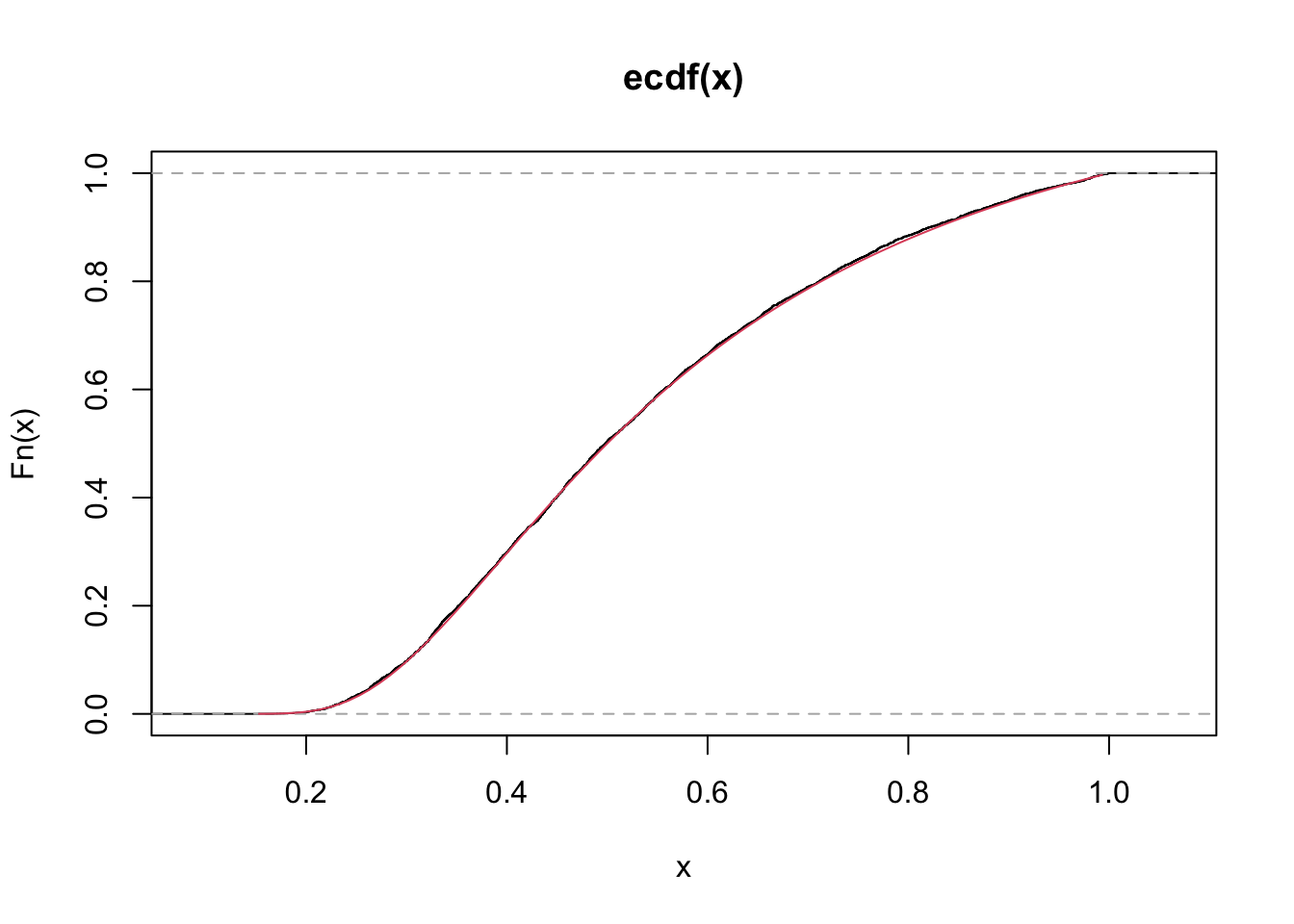
plot(quantile(x, probs = S), type = "l")
lines(qugompertz(p = S, mu = 0.5, theta = 2, tau = 0.5), col=2)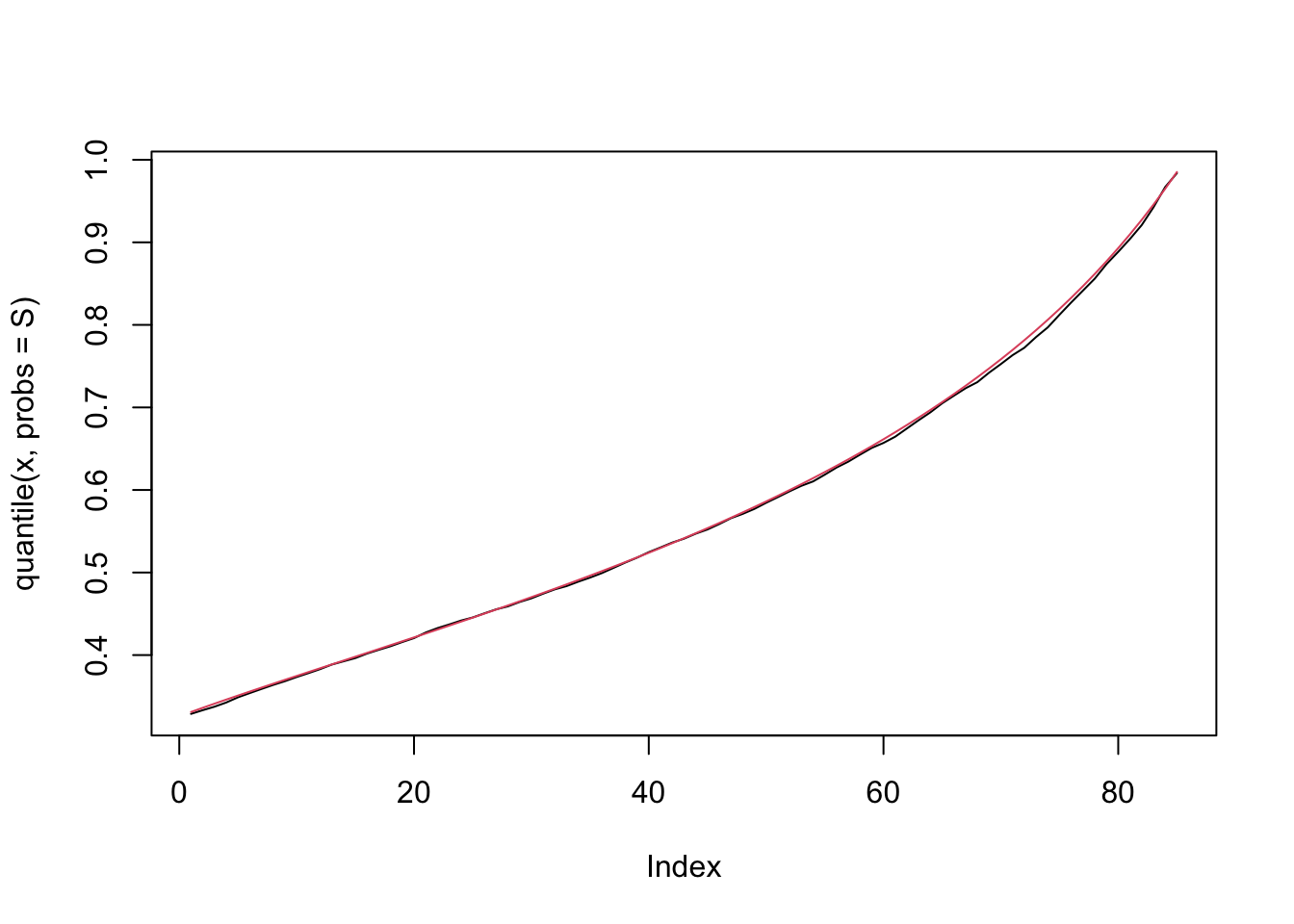

Exemplo 3.76 Em Python.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gompertz

# Gerando 5000 valores de uma distribuição Gompertz unitária
np.random.seed(123)
mu = 0.5
theta = 2
tau = 0.5

# Usando a função de distribuição inversa para gerar a amostra
x = gompertz.ppf(np.random.uniform(size=5000), c = theta, 
                 loc = mu, scale=1/tau)
R = (np.min(x), np.max(x))
S = np.arange(R[0], R[1], 0.01)

# Histograma
plt.hist(x, bins=50, density=True, color='lightgray', 
         edgecolor='black')
plt.title('Gompertz unit')

# Curva da densidade
plt.plot(S, gompertz.pdf(S, c=theta, loc=mu, scale=1 / tau), 
         color='red')
plt.show()

# Função de distribuição acumulada empírica (ECDF)
plt.plot(np.sort(x), np.arange(1, len(x) + 1) / len(x))
plt.plot(S, gompertz.cdf(S, c=theta, loc=mu, scale=1 / tau), 
         color='red')
plt.title('ECDF da Gompertz unit')
plt.show()

# Função quantil
plt.plot(S, gompertz.ppf(S, c=theta, loc=mu, scale=1 / tau), 
         color='red')
plt.title('Função quantil da Gompertz unit')
plt.show()

References

Bayes, Thomas. 1763. “An Essay Towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, FRS Communicated by Mr. Price, in a Letter to John Canton, AMFR S.” Philosophical Transactions of the Royal Society of London 1 (53): 370–418. https://www.ias.ac.in/article/fulltext/reso/008/04/0080-0088.
Billingsley, Patrick. 1986. Probability and Measure. 2nd ed. John Wiley & Sons.
Galambos, Janos, and Samuel Kotz. 1978. Characterizations of Probability Distributions: A Unified Approach with an Emphasis on Exponential and Related Models. Springer-Verlag.
Gompertz, Benjamin. 1825. “On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. In a Letter to Francis Baily, Esq. FRS &c.” Philosophical Transactions of the Royal Society of London 1 (115): 513–83. https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1825.0026.
James, B. R. 2010. “Probabilidade: Um Curso Em Nível Intermediário, Coleção Euclides.” Rio de Janeiro. IMPA, 3a. Edição. https://loja.sbm.org.br/index.php/colecoes/impa/colecao-projeto-euclides/probabilidade-um-curso-em-nivel-intermediario.html.
Johnson, Norman L, Samuel Kotz, and Narayanaswamy Balakrishnan. 1994. Continuous Univariate Distributions Vol. 1. 2nd ed. John Wiley & Sons.
———. 1995. Continuous Univariate Distributions Vol. 2. 2nd ed. John Wiley & Sons.
Kotz, Samuel, and Johan René Van Dorp. 2004. Beyond Beta: other continuous families of distributions with bounded support and applications. World Scientific. https://doi.org/10.1142/5720.
Laplace, Pierre Simon. 1812. Théorie Analytique des Probabilités. Courcier (Paris). https://gallica.bnf.fr/ark:/12148/btv1b8625611h.
Mazucheli, Josmar, André Felipe Menezes, and Sanku Dey. 2019. “Unit-Gompertz Distribution with Applications.” Statistica 79 (1): 25–43. https://rivista-statistica.unibo.it/article/download/8497/9401.
Menezes, Andr’e F. B., and Josmar Mazucheli. 2021. Unitquantreg: Parametric Quantile Regression Models for Bounded Data. https://andrmenezes.github.io/unitquantreg/.
Millard, Steven P. 2013. EnvStats: An R Package for Environmental Statistics. New York: Springer. https://link.springer.com/book/9781461484554.
Patel, Jagdish K., and Campbell B. Read. 1982. “Handbook of the Normal Distribution.” Marcel Dekker, New York.
Tong, Yung L. 1990. The Multivariate Normal Distribution. Springer-Verlag New York Inc.
Wolodzko, Tymoteusz. 2023. extraDistr: Additional Univariate and Multivariate Distributions. https://CRAN.R-project.org/package=extraDistr.
Yee, Thomas W. 2010. “The VGAM Package for Categorical Data Analysis.” Journal of Statistical Software 32 (10): 1–34. https://doi.org/10.18637/jss.v032.i10.

  1. A quantidade \(\frac{x-a}{m-a}\) está erroneamente anotada \(\frac{z-a}{z-a}\) no texto original, corrigida aqui.↩︎