3.7 Distr. Discretas Especiais

Para mais detalhes recomenda-se (Johnson, Kemp, and Kotz 2005). McLaughlin (2016) traz um compêndio de distribuições de probabilidade.

3.7.1 Uniforme discreta \(\cdot \; \mathcal{UD}(a,b)\)

\[\begin{equation} p(x|a,b) = \frac{1}{b-a+1} \tag{3.45} \end{equation}\]

onde \(a\) e \(b\) são inteiros tal que \(b \ge a\). A esperança e variância são dadas por

\[\begin{equation} E(X)=\frac{a+b}{2} \tag{3.46} \end{equation}\]

\[\begin{equation} V(X)=\frac{(b-a+1)^2-1}{12} \tag{3.47} \end{equation}\]

3.7.2 Binomial \(\cdot \; \mathcal{B}(n,p)\)

Considere um único lançamento de uma moeda que resulta em cara (\(H\)) ou coroa (\(T\)). Seja \(P(\{ H \})=p\) e \(P(\{ T \})=1-p\). Este é um ensaio de Bernoulli. Suponha agora \(n\) lançamentos independentes da mesma moeda, e seja \(X\) o número de faces cara resultantes nos \(n\) lançamentos independentes. \(X\) é uma variável aleatória (com distribuição) (de probabilidade) binomial de parâmetros \(n\) e \(p\), denotada por \(X \sim \mathcal{B}(n,p)\). A função massa de probabilidade é

\[\begin{equation} p(x|n,p) = P(X=x) = \dbinom{n}{x}p^{x}(1-p)^{n-x} \tag{3.48} \end{equation}\]

onde \(n \in \mathbb{N}, p \in \left[ 0,1 \right]\), \(x \in \left\lbrace 0, \ldots, n \right\rbrace\) e \(\dbinom{n}{x}\) é definido pela Eq. (3.19).

A esperança e variância são dadas por

\[\begin{equation} E(X)=np \tag{3.49} \end{equation}\]

\[\begin{equation} V(X)=np(1-p) \tag{3.50} \end{equation}\]

Exemplo 3.33 (Binomial) Suponha \(n=10\) lançamentos de uma moeda com \(p=0.7\). Assim, \[ X \sim \mathcal{B}(10,0.7)\] \[ p(x) = P(X=x) = \dbinom{10}{x} 0.7^{x} 0.3^{10-x} \] \[ E(X)=10 \times 0.7 = 7 \] \[ V(X)=10 \times 0.7 \times 0.3 = 2.1 \] \[ D(X) = \sqrt{2.1} \approx 1.449138 \]

barplot(dbinom(0:10, 10, 0.7), main = 'B(10,0.7)', names.arg = 0:10)

Exemplo 3.34 Em Python.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

# Parâmetros da distribuição binomial
n = 10
p = 0.7

# Valores de k
k_values = np.arange(0, 11)

# Probabilidades
probabilities = binom.pmf(k_values, n, p)

# Gráfico de barras
plt.bar(k_values, probabilities)
plt.xlabel('k')
plt.ylabel('Probabilidade')
plt.title('Distribuição Binomial B(10, 0.7)')
plt.xticks(k_values)
plt.show()

Exercício 3.17 Assista ao vídeo Uma Arma Secreta para Prever Resultados: A Distribuição Binomial do canal Primer.

3.7.3 Binomial Negativa \(\cdot \; \mathcal{BN}(k,p)\)

Considere novamente o lançamento de uma moeda que resulta em cara (\(H\), sucesso) ou coroa (\(T\), fracasso) onde \(P(\{ H \})=p\) e \(P(\{ T \})=1-p\). Seja \(X\) o ‘número de fracassos até o \(k\)-ésimo sucesso’. \(X\) é uma variável aleatória com distribuição binomial negativa de parâmetros \(k\) e \(p\), denotada por \(X \sim \mathcal{BN}(k,p)\), definida por \[\begin{equation} p(x|k,p) = P(X=x) = \dbinom{x+k-1}{x}p^{k}(1-p)^{x} \tag{3.51} \end{equation}\]

onde \(k \in \{1,2,\ldots\}\), \(0 \le p \le 1\), \(x \in \{0,1,\ldots\}\) e

\[\begin{equation} \dbinom{x+k-1}{x} = \frac{{(x+k-1)!}}{{x!(k-1)!}} \tag{3.52} \end{equation}\]

A esperança e variância são dadas por

\[\begin{equation} E(X) = \frac{k(1-p)}{p} \tag{3.53} \end{equation}\]

\[\begin{equation} V(X) = \frac{k(1-p)}{p^2} \tag{3.54} \end{equation}\]

Exemplo 3.35 (Binomial negativa) Uma moeda com \(p=0.6\) é lançada até a obtenção de \(k=4\) caras. \[ X \sim \mathcal{BN}(4,0.6),\] \[ p(x) = P(X=x) = \dbinom{x+3}{x} 0.6^{4} 0.4^{x}, \] \[ E(X) = \frac{4 \times (1-0.6)}{0.6} = \frac{8}{3} = 2.\bar{6} \] \[ V(X)= \frac{4 \times (1-0.6)}{0.6^2} = \frac{40}{9} = 4.\bar{4} \] \[ D(X) = \sqrt{\frac{40}{9}} \approx 2.108185. \]

barplot(dnbinom(0:20, 4, 0.6), main = 'BN(4,0.6)', names.arg = 0:20)

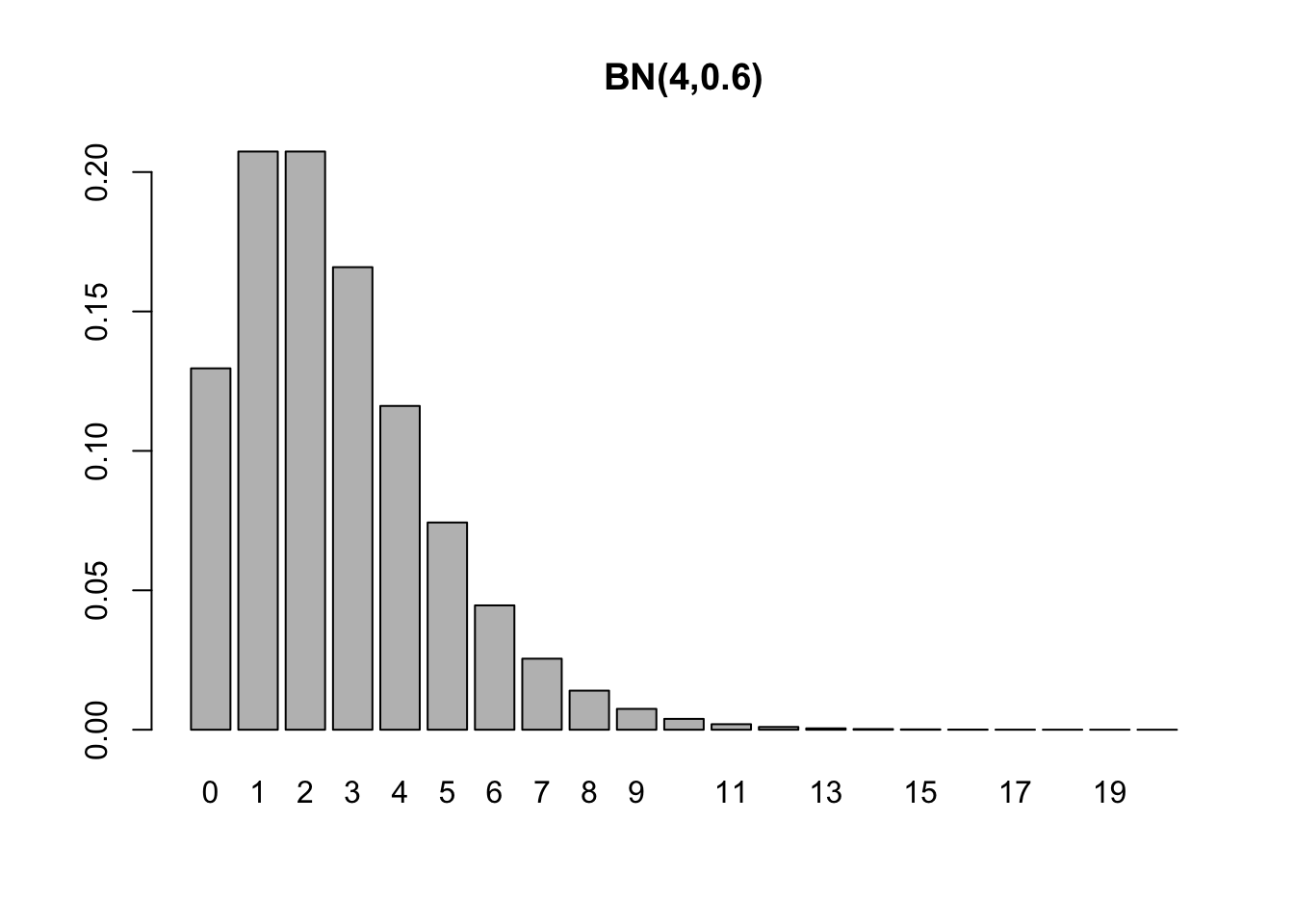
Exemplo 3.36 Em Python.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import nbinom

# Parâmetros da distribuição binomial negativa
n = 4
p = 0.6

# Valores de k
k_values = np.arange(0, 21)

# Probabilidades
probabilities = nbinom.pmf(k_values, n, p)

# Gráfico de barras
plt.bar(k_values, probabilities)
plt.xlabel('k')
plt.ylabel('Probabilidade')
plt.title('Distribuição Binomial Negativa BN(4, 0.6)')
plt.xticks(k_values, rotation=45)
plt.show()

As funções dnbinom e suas correspondentes (pbinom, qbinom e rbinom) modelam a variável \(X\) conforme Eq. (3.51). Para formulações alternativas veja este artigo da Wikipedia.

bn <- function(x,k,p){
  choose(x+k-1,x) * p^k * (1-p)^x
}
all.equal(bn(0:20, 4, 0.6), dnbinom(0:20, 4, 0.6))

## [1] TRUE

Exemplo 3.37 Em Python.

import numpy as np
from scipy.special import comb
from scipy.stats import nbinom

def bn(x, k, p):
  """
  Calcula a probabilidade da distribuição binomial negativa.

  Args:
    x: Número de falhas antes do k-ésimo sucesso.
    k: Número de sucessos.
    p: Probabilidade de sucesso.

  Returns:
    A probabilidade da distribuição binomial negativa.
  """
  return comb(x + k - 1, x) * p**k * (1 - p)**x

# Parâmetros da distribuição binomial negativa
k = 4
p = 0.6

# Valores de x
x_values = np.arange(0, 21)

# Calculando as probabilidades com a função bn()
probabilities_bn = np.array([bn(x, k, p) for x in x_values])

# Calculando as probabilidades com scipy.stats.nbinom
probabilities_scipy = nbinom.pmf(x_values, k, p)

# Comparando os resultados
print(np.allclose(probabilities_bn, probabilities_scipy))  # Output: True

3.7.4 Poisson \(\cdot \; \mathcal{P}(\lambda)\)

Siméon Denis Poisson abordou a distribuição que leva seu nome considerando o limite de uma sequência de distribuições binominais conforme Equação (3.48), no qual \(n\) tende ao infinito e \(p\) tende a zero enquanto \(np\) permanece finito igual a \(\lambda\) (Poisson 1837)²³. O termo ‘distribuição de Poisson’ (Poisson-Verteilung) foi cunhado por (Bortkewitsch 1898), ainda que Abraham de Moivre tenha derivado esta distribuição mais de um século antes (De Moivre 1718), (De Moivre 1756), (Stigler 1982).

A v.a. discreta \(X\): ‘número de sucessos por unidade de tempo’ tem distribuição Poisson de parâmetro \(\lambda\) denotada por \(X \sim \mathcal{P}(\lambda)\), onde \(x \in \left\lbrace 0, 1, 2, \ldots \right\rbrace\) e \(\lambda > 0\). A função massa de probabilidade é dada por

\[\begin{equation} p(x|\lambda) = P(X=x) = \frac{{e^{ - \lambda } \lambda ^x }}{{x!}} \tag{3.55} \end{equation}\]

onde o número de Euler²⁴ tem valor aproximado \(e \approx 2.71828\;18284\;59045\). A esperança e variância são dadas por \[\begin{equation} E(X)=\lambda \tag{3.56} \end{equation}\]

\[\begin{equation} V(X)=\lambda \tag{3.57} \end{equation}\]

Exemplo 3.38 (Poisson) Considere um pedágio onde passam em média \(\lambda = 2\) veículos por minuto. Assim, \[ X \sim \mathcal{P}(2),\] \[ p(x) = P(X=x) = \frac{{e^{- 2} 2^{x} }}{{x!}}, \] \[ E(X)=2, \] \[ V(X)=2. \] \[ D(X) = \sqrt{2} \approx 1.4142. \]

barplot(dpois(0:10, 2), main = 'P(2)', names.arg = 0:10)

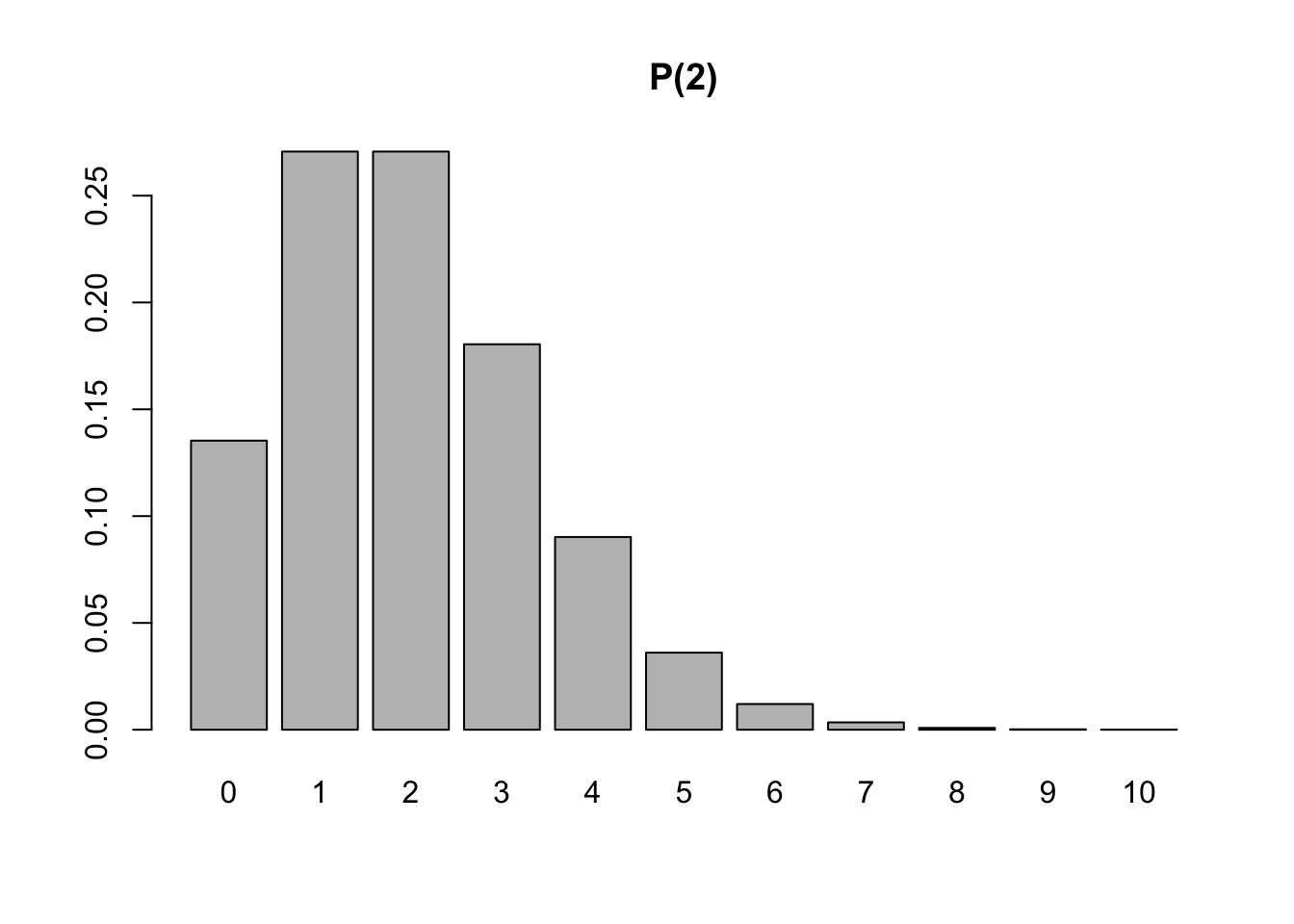
Exercício 3.18 Considere a distribuição de Poisson definida pela Eq. (3.55).

1. Mostre que a função descrita pela Eq. (3.55) é uma função massa de probabilidade. Dica²⁵: \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\).
2. Mostre que \(E(X)\) é dada pela Eq. (3.56).
3. Mostre que \(V(X)\) é dada pela Eq. (3.57). Dica: \(\sum_{x=1}^{\infty} \frac{x \lambda^{x-1}}{(x-1)!} = (\lambda+1)e^{\lambda}\).

3.7.5 Hipergeométrica \(\cdot \; \mathcal{H}(N,R,n)\)

Suponha uma urna com \(N\) bolinhas das quais \(R\) são marcadas com um \(\times\), de onde retira-se uma amostra de \(n\) bolinhas. Seja \(X\) o número de bolinhas marcadas com \(\times\) das \(n\) sorteadas. \(X\) tem distribuição hipergeométrica denotada por \(X \sim \mathcal{H}(N,R,n)\), onde \(x \in \{0,1,\ldots,n\}\), \(N \in \{1,2,\ldots\}\), \(R \in \{1,2,\ldots,N\}\), \(n \in \{1,2,\ldots,N\}\).

Sua função (massa) de probabilidade é definida por

\[\begin{equation} p(x|N,R,n) = P(X=x|N,R,n) = \frac{{R \choose x}{N-R \choose n-x}}{{N \choose n}} \tag{3.58} \end{equation}\]

A esperança e variância são dadas por \[\begin{equation} E(X) = n \frac{R}{N} \tag{3.59} \end{equation}\]

\[\begin{equation} V(X) = n \frac{N-n}{N-1} \frac{R}{N} \left( 1-\frac{R}{N} \right) \tag{3.60} \end{equation}\]

Exemplo 3.39 (Hipergeométrica) Suponha uma urna com \(N=15\) bolinhas, \(R=10\) marcadas com um \(\times\) de onde se retira uma amostra de \(n=7\) bolinhas.

barplot(dhyper(0:7,10,5,7), main = 'H(15,10,7)', names.arg = 0:7)

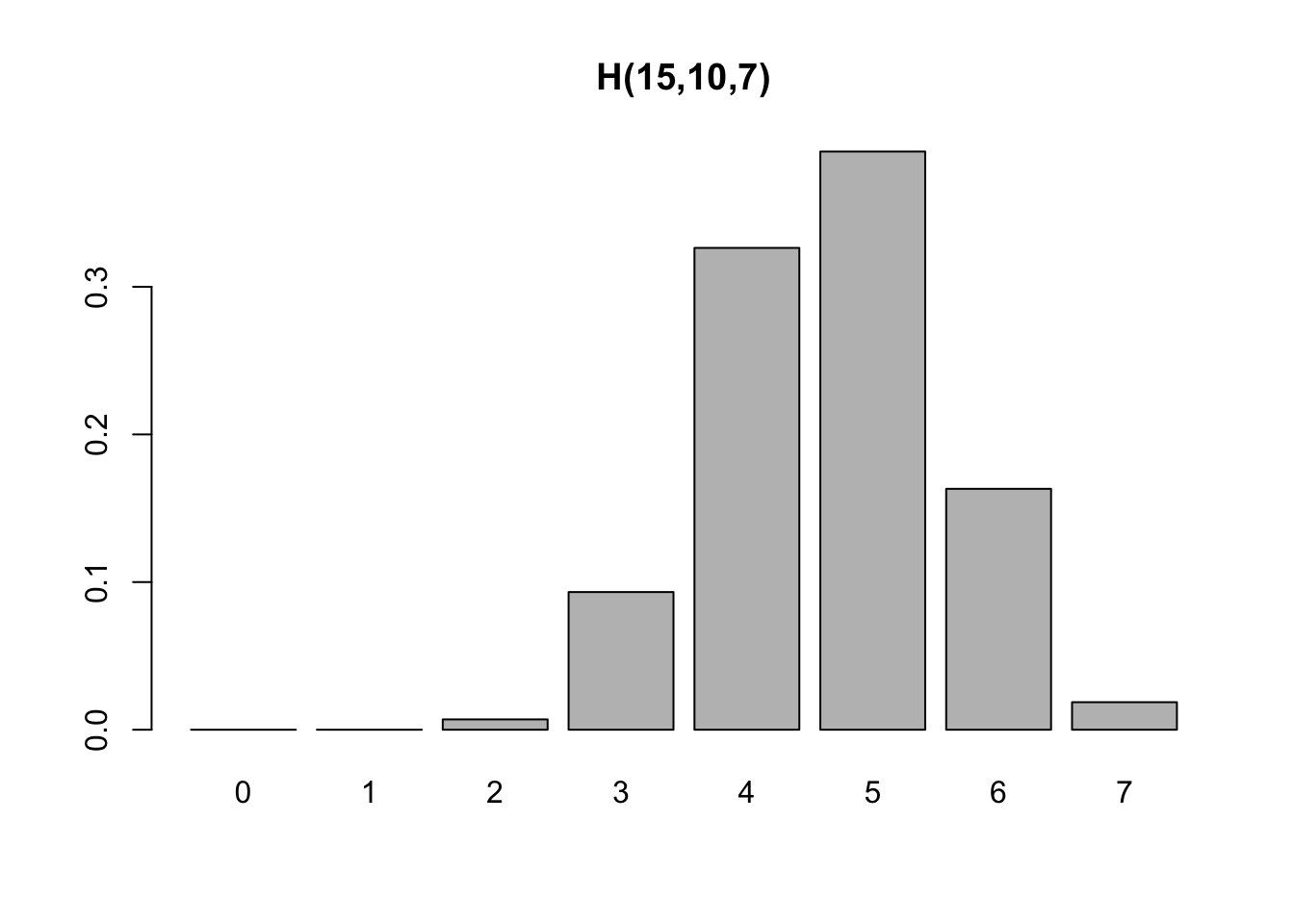
Exemplo 3.40 Em Python.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import hypergeom

# Parâmetros da distribuição hipergeométrica
M = 15  # Tamanho da população
n = 10  # Número de sucessos na população
N = 7   # Tamanho da amostra

# Valores de x
x_values = np.arange(0, 8)

# Probabilidades
probabilities = hypergeom.pmf(x_values, M, n, N)

# Gráfico de barras
plt.bar(x_values, probabilities)
plt.xlabel('x')
plt.ylabel('Probabilidade')
plt.title('Distribuição Hipergeométrica H(15, 10, 7)')
plt.xticks(x_values)
plt.show()

3.7.6 Bernoulli-Poisson \(\cdot \; \mathcal{BP}(p,\lambda_1,\lambda_2)\)

Uma variável aleatória \(X\) possui distrubuição Bernoulli-Poisson parametrizada por \(p\), \(\lambda_1\) e \(\lambda_2\) se assume distribuição Poisson de taxa \(\lambda_1\) com probabilidade \(p\) e distribuição Poisson de taxa \(\lambda_2\) com probabilidade \(1-p\). Simbolicamente \(X \sim \mathcal{BP}(p,\lambda_1,\lambda_2)\), \(x \in \{ 0,1,\ldots \}\), \(p \in \left[ 0,1 \right]\), \(\lambda_1,\lambda_2 > 0\), i.e.,

\[\begin{equation} X \sim \left\{ \begin{array}{l} \mathcal{P}(\lambda_1) \;\; \text{com probabilidade} \;\; p \\ \mathcal{P}(\lambda_2) \;\; \text{com probabilidade} \;\; 1-p \\ \end{array} \right. \tag{3.61} \end{equation}\]

Sua função massa de probabilidade é \[\begin{equation} p(x|p,\lambda_1,\lambda_2) =\frac{e^{-\lambda_1} \lambda_{1}^{x}}{x!} p + \frac{e^{-\lambda_2} \lambda_{2}^{x}}{x!} (1-p) \tag{3.62} \end{equation}\]

Sua esperança e variância são dadas por \[\begin{equation} E(X) = (\lambda_1 - \lambda_2)p + \lambda_2 \tag{3.63} \end{equation}\] \[\begin{equation} V(X) = -(\lambda_1 - \lambda_2)^2 p^2 + \left[ (\lambda_1 - \lambda_2)^2 + \lambda_1 - \lambda_2 \right] p + \lambda_2 \tag{3.64} \end{equation}\]

Exemplo 3.41 Considere a v.a. \(X \sim \mathcal{BP}(0.2,1,15)\).

# Função massa de probabilidade Bernoulli-Poisson
dbp <- function(x,p,lambda1,lambda2){
  v <- dpois(x,lambda1)*p + dpois(x,lambda2)*(1-p)
  return(v)
}
p <- 0.2
l1 <- 1
l2 <- 15
barplot(dbp(0:30,p,l1,l2))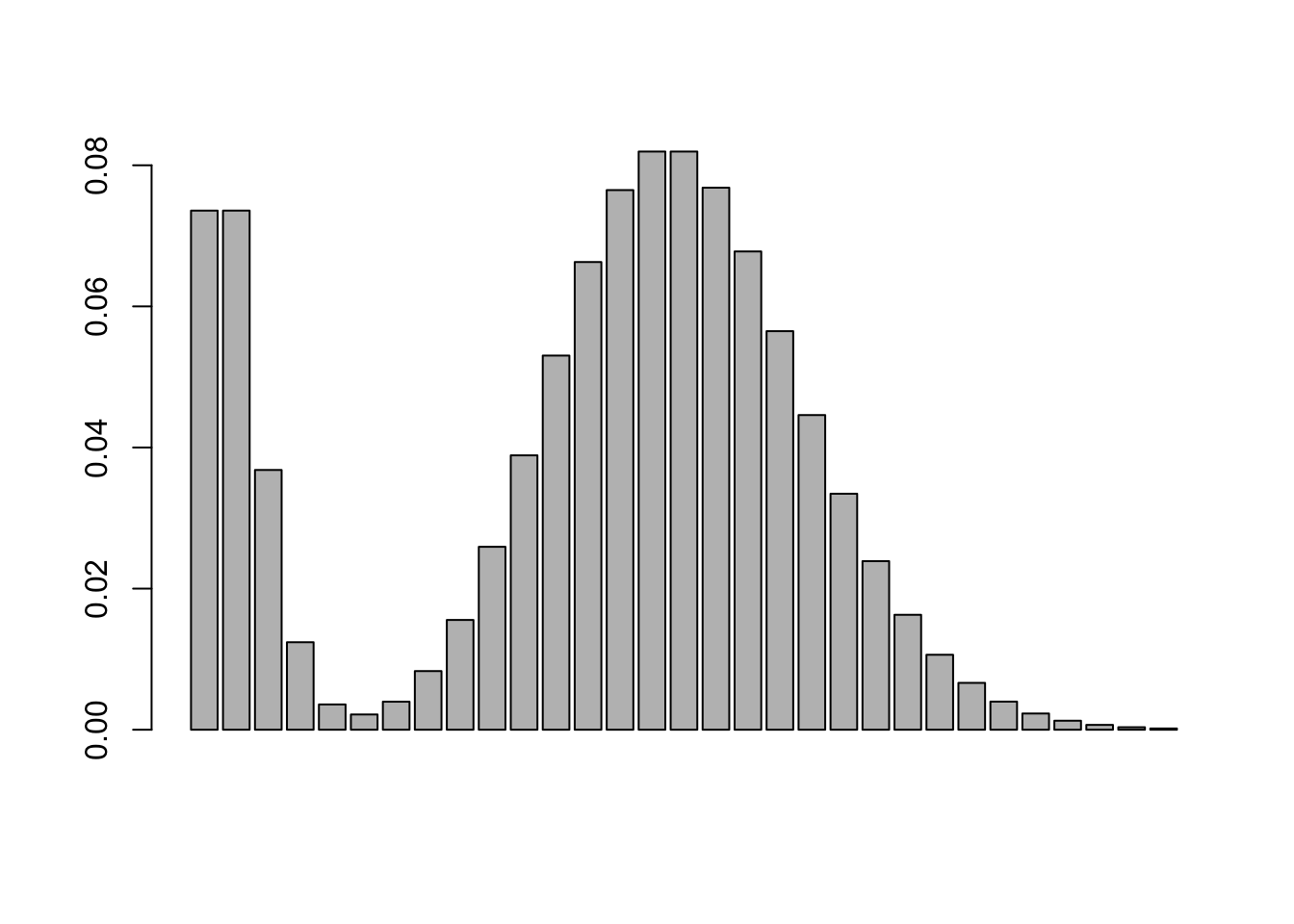

# Média teórica
(EX <- (l1-l2)*p+l2)

## [1] 12.2

# Variância teórica
(VX <- -(l1-l2)^2*p^2+((l1-l2)^2+l1-l2)*p+l2)

## [1] 43.56

Exemplo 3.42 Em Python.

import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt

# Função massa de probabilidade Bernoulli-Poisson
def dbp(x, p, lambda1, lambda2):
  """
  Calcula a função massa de probabilidade da distribuição Bernoulli-Poisson.

  Args:
    x: Valor da variável aleatória.
    p: Probabilidade de sucesso na distribuição Bernoulli.
    lambda1: Taxa da primeira distribuição Poisson.
    lambda2: Taxa da segunda distribuição Poisson.

  Returns:
    A probabilidade de x na distribuição Bernoulli-Poisson.
  """
  v = poisson.pmf(x, lambda1) * p + poisson.pmf(x, lambda2) * (1 - p)
  return v

# Parâmetros
p = 0.2
l1 = 1
l2 = 15

# Valores de x
x_values = np.arange(0, 31)

# Calculando as probabilidades
probabilities = np.array([dbp(x, p, l1, l2) for x in x_values])

# Gráfico de barras
plt.bar(x_values, probabilities)
plt.xlabel('x')
plt.ylabel('Probabilidade')
plt.title('Distribuição Bernoulli-Poisson')
plt.show()

# Média teórica
EX = (l1 - l2) * p + l2
print(f"Média teórica (EX): {EX:.4f}")  # Output: 12.2000

# Variância teórica
VX = -(l1 - l2)**2 * p**2 + ((l1 - l2)**2 + l1 - l2) * p + l2
print(f"Variância teórica (VX): {VX:.4f}")  # Output: 16.9600

Exercício 3.19 Considere a distribuição Bernoulli-Poisson definida pela Eq. (3.62).

1. Mostre que a função descrita pela Eq. (3.62) é uma função (massa) de probabilidade. Dica: \(\sum_{x=0}^{\infty} \frac{\lambda^x}{x!} = e^\lambda\).
2. Mostre que \(E(X)\) é dada pela Eq. (3.63).
3. Mostre que \(V(X)\) é dada pela Eq. (3.64). Dica: \(\sum_{x=1}^{\infty} \frac{x \lambda^{x-1}}{(x-1)!} = (\lambda+1)e^{\lambda}\).

References

Boros, George, and Victor Moll. 2004. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge University Press.

Bortkewitsch, L von. 1898. Das Gesetz Der Kleinen Zahlen. Teubner (Leipzig). https://ia803406.us.archive.org/13/items/dasgesetzderklei00bortrich/.

De Moivre, Abraham. 1718. The Doctrine of Chances: Or, a Method of Calculating the Probabilities of Events in Play. 1st ed. London: printe for A. Millar, in the Strand. https://archive.org/details/b30412390.

———. 1756. The Doctrine of Chances: Or, a Method of Calculating the Probabilities of Events in Play. 3rd ed. London: printe for A. Millar, in the Strand. https://archive.org/details/doctrineofchance00moiv.

Johnson, Norman L, Adrienne W Kemp, and Samuel Kotz. 2005. Univariate Discrete Distributions. 3rd ed. John Wiley & Sons.

Poisson, Siméon-Denis. 1837. Recherches Sur La Probabilité Des Jugements En Matière Criminelle Et En Matière Civile: Précédées Des règles générales Du Calcul Des Probabilités. Bachelier. https://archive.org/details/bub_gb__8FAjzHfzHgC/mode/2up.

Stigler, Stephen M. 1982. “Poisson on the Poisson Distribution.” Statistics & Probability Letters 1 (1): 33–35. http://www.medicine.mcgill.ca/epidemiology/hanley/statbook/StiglerPoisson.pdf.

---

23. Seções 73, pp. 189-190, e 81, pp. 205-207. Veja (Johnson, Kemp, and Kotz 2005, 156).↩︎

24. Na literatura também pode ser conhecido como número de Napier, constante de Napier/neperiana, entre outras formas. Não confundir com a constante de Euler–Mascheroni \(\gamma \approx 0.57721\;56649\;01532\;86061\).↩︎

25. (Boros and Moll 2004, 91)↩︎