7.2 Regressão Linear Simples

A palavra “regressão” não constitui escolha feliz sob o ponto de vista etimológico, mas já está tão arraigada na literatura estatística que não tentamos substituí-la por outra que exprimisse mais convenientemente suas propriedades essenciais. Foi introduzida por Galton, em conexão com a hereditariedade da estatura. Galton verificou que os filhos de pais cujas estaturas se afastam \(x\) polegadas em relação à estatura média de todos os pais, apresentam um desvio em relação à estatura média de todos os filhos inferior a \(x\) polegadas, isto é, verifica-se o que Galton chamou de “regressão à mediocridade”. Em geral, a idéia ligada à palavra “regressão” nada tem a ver com êste sentido, devendo ser considerada apenas como expressão convencional. (G. Udny Yule and Kendall 1948, 246)

Para maiores detalhes veja (Galton 1889, 95–99) e (Stigler 1997).

7.2.1 Reta

A equação da reta é uma relação matemática utilizada para descrever uma reta no plano cartesiano. Pode ser apresentada de formas distintas, sendo que na Seção 7.2.2 é utilizada a notação da reta reduzida, fazendo \(a' = \beta_{1}\) e \(b' = \beta_{0}\).

Tipo Equação
Geral \(ax + by + c = 0\)
Segmentária \(\frac{x}{-c/a} + \frac{y}{-c/b} = 1\)
Reduzida \(y = -\frac{a}{b} x - \frac{c}{b} \; \therefore \; y = a'x + b'\)

Exemplo 7.12 (Equação reduzida) Considere a reta que passa pelos pontos \(A = (0,-3)\) e \(B = (1.5,0)\).

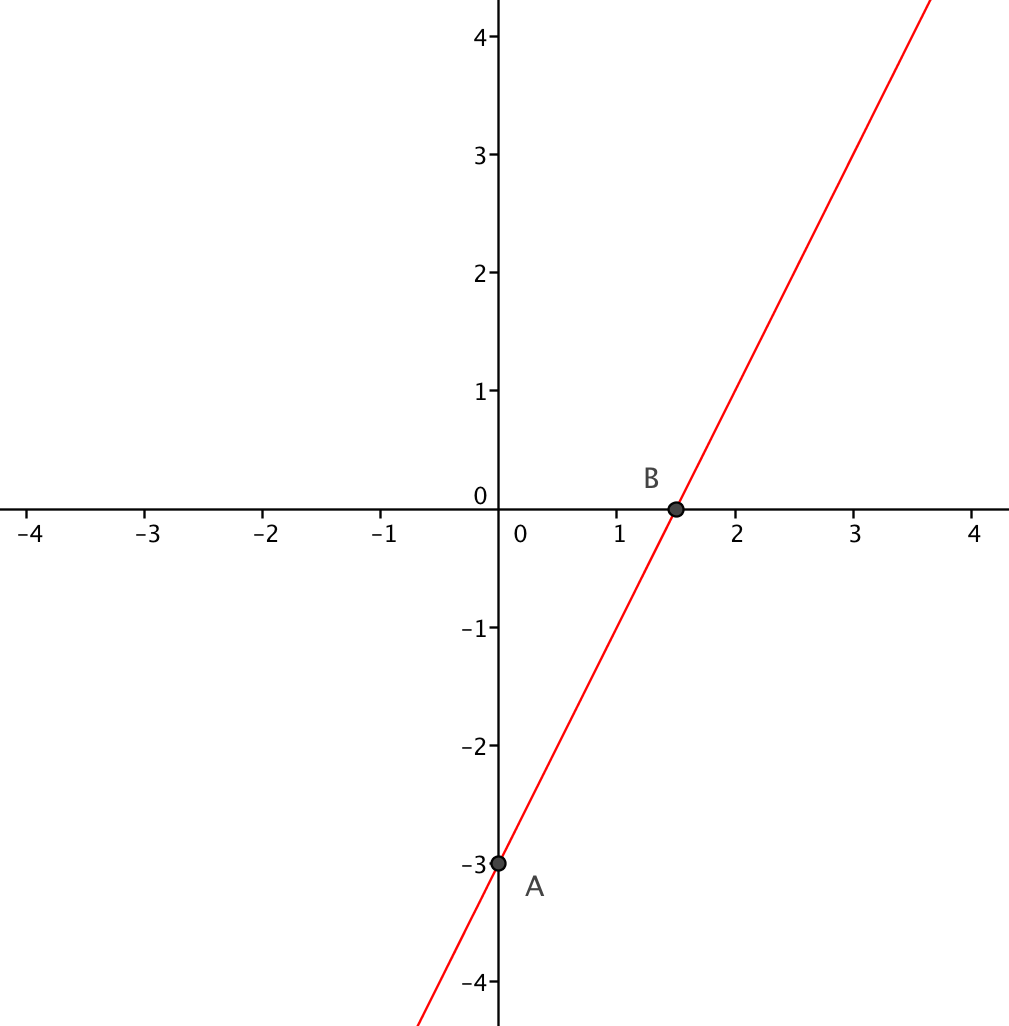
Uma maneira de descobrir a equação reduzida é substituir os pontos \(A\) e \(B\) em \(y = a'x + b'\):

Ponto Valores de \(a'\) e \(b'\)
\(A\) \(-3 = a' \times 0 + b' \; \therefore \; b' = -3\)
\(B\) \(0 = a' \times 1.5 + (-3) \; \therefore \; a' = \frac{3}{1.5} = 2\)

Assim, a equação reduzida da reta é \(y = 2x - 3\), onde a inclinação é \(a' = 2\) e o intercepto (constante ou coeficiente linear) é \(b' = -3\). Para cada aumento de 1 unidade em \(x\), \(y\) aumenta 2 unidades.

Exemplo 7.13 (Equação segmentária) Do Exemplo 7.12, pode-se obter a equação segmentária da reta a partir da forma reduzida. \[y = 2x - 3 \; \therefore \; 2x - y = 3 \; \therefore \; \frac{2}{3} x - \frac{1}{3} y = \frac{3}{3} \; \therefore \; \frac{x}{3/2} + \frac{y}{3/-1} = 1 \; \therefore \; \frac{x}{1.5} + \frac{y}{-3} = 1.\] Assim, \(-c/a = 1.5\) e \(-c/b = -3\). Note que \(x_{B} = 1.5\) e \(y_{A} = -3\).

Exemplo 7.14 (Equação geral) Do Exemplo 7.12, pode-se obter a equação geral da reta a partir da forma reduzida. \[y = 2x - 3 \; \therefore \; 2x - y - 3 = 0.\] Assim, \(a = 2\), \(b = -1\) e \(c = -3\). Note que \(a' = - \frac{2}{-1} = 2\) e \(b' = - \frac{-3}{-1} = -3\).

7.2.2 Modelo

O modelo de regressão linear simples (RLS) populacional/universal é construído, na abordagem clássica, com todos os \(N\) pares ordenados da população ou universo, i.e., \((x_i,y_i), \; i \in \{1,\ldots,N\}\). Pode ser descrito pela Eq. (7.13).

\[\begin{equation} y_i = \beta_0 + \beta_1 x_i + \varepsilon_i, \tag{7.13} \end{equation}\] onde supõe-se \(\varepsilon \sim \mathcal{N}(0,\sigma_{\varepsilon})\).

Exemplo 7.15 No gráfico a seguir pode-se notar que a linha azul refere-se à média \(\widehat{E(Y)}=\bar{y}=180\). Este valor é constante – ou incondicional – para qualquer valor de \(x\) (no caso a temperatura máxima do dia na escala Celsius). Já a linha vermelha pontilhada indica que espera-se um valor baixo de \(y\) (no caso o número de garrafas vendidas no dia) quanto menor o \(x\), e alto \(y\) quanto maior o \(x\).

plot(dr$temp, dr$gar, xlab = 'x', ylab = 'y', las = 1)
abline(h = mean(dr$gar), col = 'blue')
abline(a = -19.11, b = 5.91, col = 'red', lty = 2)
legend(26, 235, legend=c('Incondicional','Condicional'),
       col = c('blue', 'red'), lty = 1:2, cex = 0.8, box.lty = 0)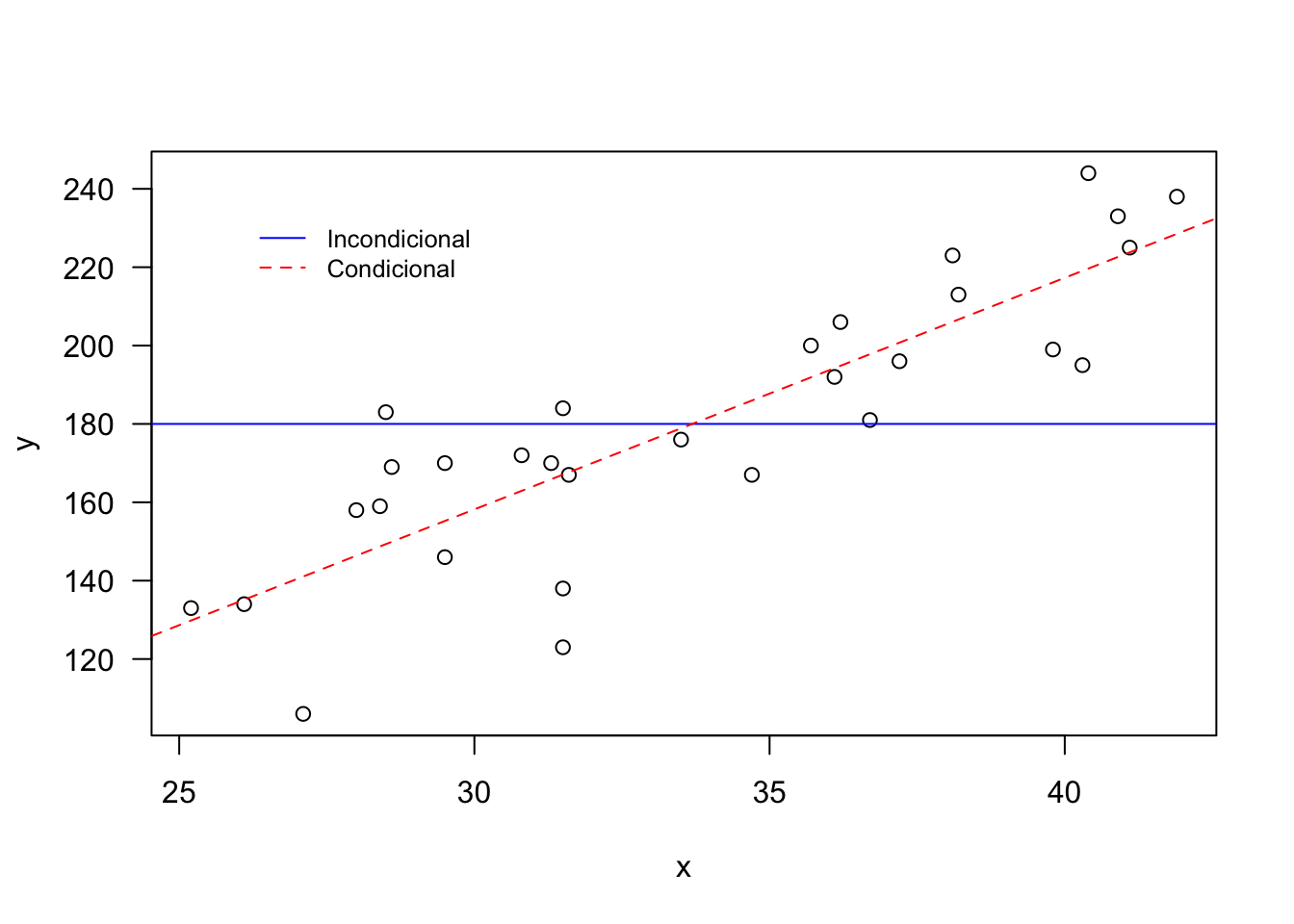

Exemplo 7.16 Em Python.

import pandas as pd
import matplotlib.pyplot as plt

# Load the data
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Create the scatter plot
plt.scatter(dr['temp'], dr['gar'], label="Data")

# Calculate and plot the mean line
mean_gar = dr['gar'].mean()
plt.axhline(y=mean_gar, color='blue', linestyle='-', 
            label='Incondicional')

# Plot the regression line
plt.plot(dr['temp'], -19.11 + 5.91 * dr['temp'], color='red', 
         linestyle='--', label='Condicional')

# Add labels and title
plt.xlabel('temp') # x label
plt.ylabel('gar') # y label
plt.title("Scatter Plot with Mean and Regression Lines")

# Add legend
plt.legend(loc='upper left', fontsize='small', frameon=False)

# Show the plot
plt.show()

7.2.2.1 Estimativa dos parâmetros

Na maioria dos casos práticos trabalha-se com amostras, sendo necessário estimar os valores de \(\beta_0\) e \(\beta_1\). O método dos mínimos quadrados pode ser utilizado para calcular estas estimativas. O princípio do método é minimizar a soma de quadrado dos erros, i.e., \[\begin{equation} \text{minimizar} \sum_{i=1}^n \varepsilon_{i}^{2}. \tag{7.14} \end{equation}\]

Basicamente utiliza-se \(\varepsilon_i = y_i - \beta_0 - \beta_1 x_i\) da Eq. (7.13) e deriva-se parcialmente em relação a \(\beta_0\) e \(\beta_1\), fazendo cada uma das derivadas parciais igual a zero. Para maiores detalhes recomenda-se (DeGroot and Schervish 2012, 689). As estimativas por mínimos quadrados são enfim dadas por \[\begin{equation} \hat{\beta}_1 = \frac{n \sum{xy} - \sum{x} \sum{y}}{n \sum{x^2} - (\sum{x})^2} \tag{7.15} \end{equation}\] \[\begin{equation} \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} \tag{7.16} \end{equation}\]

Exemplo 7.17 Considere novamente os dados do Exemplo 7.1. Pode-se ajustar um modelo linear simples conforme Equações (7.13), (7.15) e (7.16). Note a estimativa na forma \(y = -19.11 + 5.91 x\).

(fit <- lm(gar ~ temp, data = dr))
## 
## Call:
## lm(formula = gar ~ temp, data = dr)
## 
## Coefficients:
## (Intercept)         temp  
##     -19.110        5.915

Exemplo 7.18 Em Python.

import pandas as pd
import statsmodels.formula.api as smf

# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Ajustando o modelo de regressão linear
fit = smf.ols('gar ~ temp', data=dr).fit()

# Imprimindo o resumo do modelo
print(fit.summary())

7.2.2.2 Modelo RPO

Um modelo na forma da Eq. (7.17) é chamado regressão pela origem (RPO) pelo fato de a reta ajustada passar pelo ponto \((0,0)\), a origem do plano cartesiano. Para mais detalhes veja (Eisenhauer 2003). \[\begin{equation} y_i = \beta_1^{*} x_i + \varepsilon_i, \tag{7.17} \end{equation}\] onde \(\varepsilon_i \sim \mathcal{N}(0,\sigma_{\varepsilon})\). A estimativa do parâmetro \(\beta_1^{*}\) é dada por \[\begin{equation} \hat{\beta}_1^{*} = \frac{\sum{xy} }{\sum{x^2} }. \tag{7.18} \end{equation}\]

Exemplo 7.19 Considere novamente os dados do Exemplo 7.1. Pode-se ajustar um modelo RPO conforme Equações (7.17) e (7.18), resultando em \(y = 5.36 x\). Na função stats::lm() é possível fazer o ajuste utilizando + 0 no lugar de - 1.

(fit0 <- lm(gar ~ temp - 1, data = dr))
## 
## Call:
## lm(formula = gar ~ temp - 1, data = dr)
## 
## Coefficients:
##  temp  
## 5.359

Exemplo 7.20 Em Python.

import pandas as pd
import statsmodels.formula.api as smf

# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Ajustando o modelo de regressão linear sem intercepto
fit0 = smf.ols('gar ~ temp - 1', data=dr).fit()

# Imprimindo o resumo do modelo
print(fit0.summary())

Exercício 7.6 Considere novamente os dados dos Exemplos 7.1 e 7.17.

  1. Calcule a estimativa dos parâmetros do modelo descrito na Equação (7.13) considerando as Equações (7.15) e (7.16).
  2. Calcule a estimativa dos parâmetros do modelo descrito na Equação (7.17) considerando a Equação (7.18).

Exercício 7.7 Obtenha os estimadores (7.16) e (7.15) a partir da Eq. (7.14).

7.2.3 Diagnóstico inferencial

O diagnóstico inferencial consiste em avaliar a qualidade de um modelo em relação à estimação de seus parâmetros (\(\theta\)).

7.2.3.1 Teste para \(\beta_0\)

As hipóteses usuais do teste para \(\beta_0\) são \(H_0: \beta_0 = 0\) vs \(H_1: \beta_0 \ne 0\). Sob \(H_0\) \[\begin{equation} T_0 = \frac{\hat{\beta}_0}{ep(\hat{\beta}_0)} \sim t_{n-2} \tag{7.19} \end{equation}\] onde \(\hat{\beta}_0\) é dado pela Eq. (7.16) e \[\begin{equation} ep(\hat{\beta}_0) = \sqrt{\hat{\sigma}^2 \left[ \frac{1}{n} + \frac{\bar{x}^2}{S_{xx}} \right] } = \sqrt{\frac{\sum_{i=1}^n (y_i - \hat{y}_i)^2}{n-2} \left[ \frac{1}{n} + \frac{\bar{x}^2}{\sum_{i=1}^n (x_i - \bar{x})^2} \right] } \tag{7.20} \end{equation}\]

7.2.3.2 Teste para \(\beta_1\)

No teste para \(\beta_1\) decide-se a respeito da presença ou ausência de relação linear entre \(X\) e \(Y\). As hipóteses usuais do teste para \(\beta_1\) são \(H_0: \beta_1 = 0\) vs \(H_1: \beta_1 \ne 0\). Sob \(H_0\) \[\begin{equation} T_1 = \frac{\hat{\beta}_1}{ep(\hat{\beta}_1)} \sim t_{n-2} \tag{7.21} \end{equation}\] onde \(\hat{\beta}_1\) é dado pela Eq. (7.15) e \[\begin{equation} ep(\hat{\beta}_1) = \sqrt{\frac{\hat{\sigma}^2}{S_{xx}}} = \sqrt{\frac{\sum_{i=1}^n (y_i - \hat{y}_i)^2 / (n-2)}{\sum_{i=1}^n (x_i - \bar{x})^2} } \tag{7.22} \end{equation}\]

7.2.3.3 Teste para \(\beta_1^{*}\)

\[\begin{equation} T_1^{*} = \frac{\hat{\beta}_1^{*}}{ep(\hat{\beta}_1^{*})} \sim t_{n-1} \tag{7.23} \end{equation}\] onde \(\hat{\beta}_1^{*}\) é dado pela Eq. (7.18) e \[\begin{equation} ep(\hat{\beta}_1^{*}) = \sqrt{\frac{\hat{\sigma}^2}{S_{xx}}} = \sqrt{\frac{\sum_{i=1}^n (y_i - \hat{y}_i)^2 / (n-1)}{\sum_{i=1}^n x_{i}^{2} } } \tag{7.24} \end{equation}\]

7.2.3.4 Critérios de informação

AIC - Critério de Informação de Akaike

(Akaike 1974) propõe um critério teórico de informação conforme Eq. (7.25). Quanto menor o valor da medida, melhor (no sentido de mais parcimonioso) é o modelo.

\[\begin{equation} \text{AIC} = -2 l(\hat{\beta}) + 2n_{par}, \tag{7.25} \end{equation}\]

onde \(n_{par}\) indica o número de parâmetros ajustados independentemente no modelo e \(l(\hat{\beta})\) é o logaritmo do valor de máxima verossimilhança do modelo. Para mais detalhes veja as documentações de stats::AIC() e stats::logLik().

BIC - Critério de Informação Bayesiano

(Schwarz 1978) propõe um critério teórico de informação conforme Eq. (7.26). O autor argumenta48 que tanto o AIC quanto o BIC fornecem uma formulação matemática do princípio da parcimônia na construção de modelos. Porém, para um grande número de observações, os dois critérios podem diferir bastante entre si, sendo mais indicado dar preferência ao BIC.

\[\begin{equation} \text{BIC} = -2 l(\hat{\beta}) + \log(n) n_{par}, \tag{7.26} \end{equation}\]

Exemplo 7.21 Considere o Exemplo 7.17. Pode-se utilizar a função genérica base::summary() para realizar o diagnóstico dos modelos considerados. O modelo RLS na forma \(y=-19.1096+5.9147x\) foi atribuído ao objeto fit.

summary(fit)
## 
## Call:
## lm(formula = gar ~ temp, data = dr)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -44.204  -8.261   3.518  10.796  33.540 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -19.1096    22.9195  -0.834    0.411    
## temp          5.9147     0.6736   8.780 1.57e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.24 on 28 degrees of freedom
## Multiple R-squared:  0.7336, Adjusted R-squared:  0.7241 
## F-statistic:  77.1 on 1 and 28 DF,  p-value: 1.565e-09

Exemplo 7.22 Em Python.

import pandas as pd
import statsmodels.formula.api as smf

# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Ajustando o modelo de regressão linear
fit = smf.ols('gar ~ temp', data=dr).fit()

# Imprimindo o resumo do modelo
print(fit.summary())

O modelo RPO na forma \(y=5.35904x\) foi atribuído ao objeto fit0.

summary(fit0)
## 
## Call:
## lm(formula = gar ~ temp - 1, data = dr)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -45.810 -10.537   3.503  11.979  30.267 
## 
## Coefficients:
##      Estimate Std. Error t value Pr(>|t|)    
## temp  5.35904    0.09734   55.05   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 18.14 on 29 degrees of freedom
## Multiple R-squared:  0.9905, Adjusted R-squared:  0.9902 
## F-statistic:  3031 on 1 and 29 DF,  p-value: < 2.2e-16

Exemplo 7.23 Em Python.

import pandas as pd
import statsmodels.formula.api as smf

# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Ajustando o modelo de regressão linear sem intercepto
fit0 = smf.ols('gar ~ temp - 1', data=dr).fit()

# Imprimindo o resumo do modelo
print(fit0.summary())

Os critérios de informação de Akaike (AIC) e Schwartz (BIC) podem ser calculados respectivamente via stats::AIC() e stats::BIC(). Os dois critérios sugerem que o modelo RPO é mais parcimonioso do que o modelo RLS.

AIC(fit); BIC(fit)    # RLS
## [1] 263.2736
## [1] 267.4772
AIC(fit0); BIC(fit0)  # RPO
## [1] 262.0094
## [1] 264.8118

Exemplo 7.24 Em Python.

import pandas as pd
import statsmodels.formula.api as smf

# Dados (se ainda não estiverem carregados)
dr = pd.read_csv('https://filipezabala.com/data/drinks.txt', 
                 sep = '\t')

# Ajustando os modelos
fit = smf.ols('gar ~ temp', data=dr).fit()
fit0 = smf.ols('gar ~ temp - 1', data=dr).fit()

# Calculando AIC e BIC
print(f"AIC (RLS): {fit.aic:.4f}")
print(f"BIC (RLS): {fit.bic:.4f}")
print(f"AIC (RPO): {fit0.aic:.4f}")
print(f"BIC (RPO): {fit0.bic:.4f}")

7.2.3.5 Diagnóstico gráfico

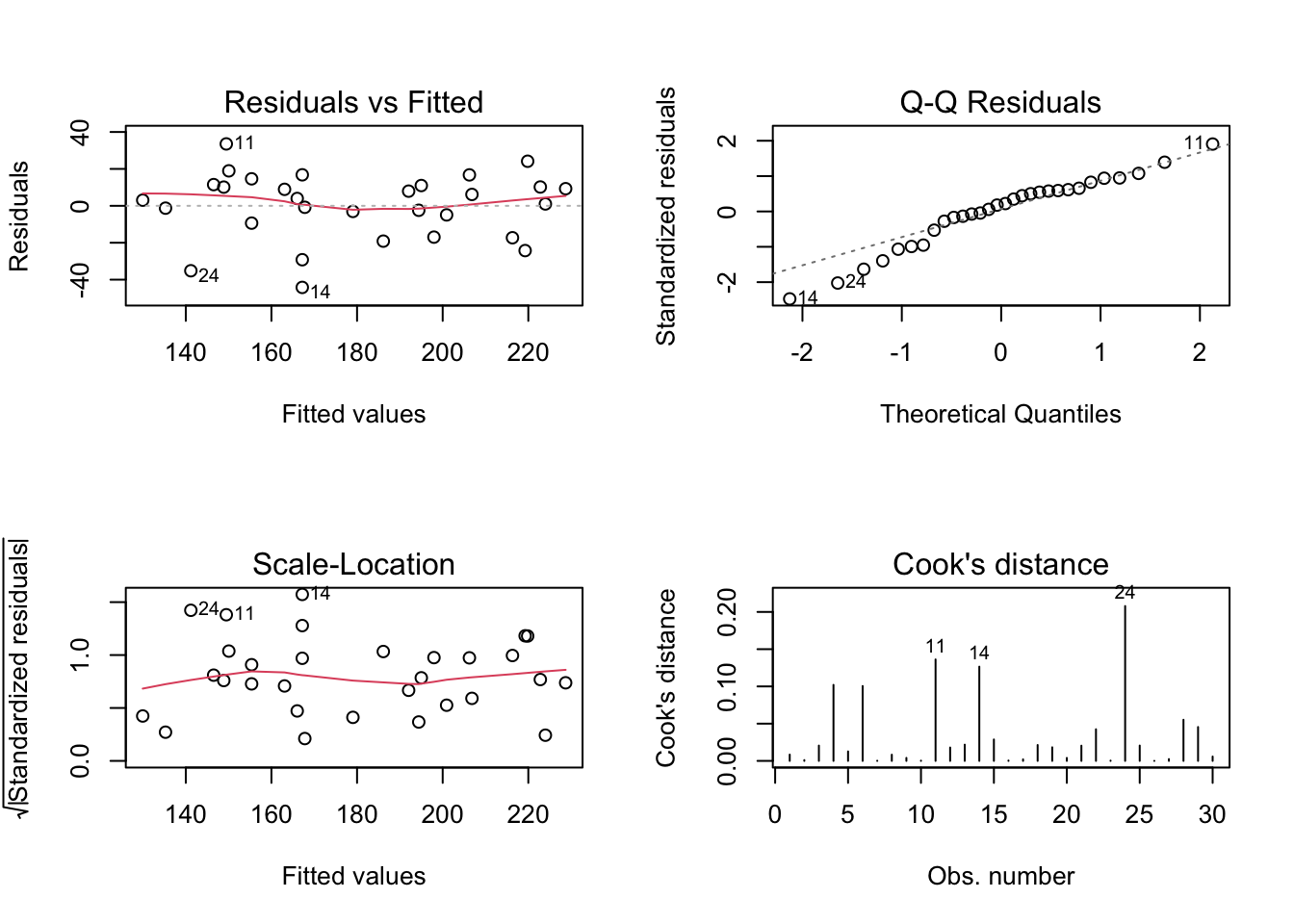
Pode-se ainda realizar uma inspeção visual como complemento da análise inferencial. Para um modelo bem ajustado espera-se:

  • ‘Residuals vs Fitted’ e ‘Scale-Lacation’ não indicando qualquer tipo de tendência ou comportamento modelável.
  • ‘Q-Q Residuals’ apresentando pontos o mais próximo possível da linha pontilhada, que indica normalidade perfeita dos resíduos.
  • ‘Cook’s distance’ não indicando possíveis pontos influentes, que poderiam estar contribuindo de maneira desproporcional ao modelo. Para mais detalhes veja a documentação de stats::lm.influence(), (R. D. Cook 1977) e (Paula 2024).

Exemplo 7.25 Apresentando o diagnóstico gráfico do modelo completo. Teste plot(fit0, which = 1:4) e compare os resultados.

par(mfrow = c(2,2))
plot(fit, which = 1:4)

Exemplo 7.26 Em Python.

import matplotlib.pyplot as plt
import statsmodels.api as sm

# Ajustando os modelos (se ainda não estiverem ajustados)
# ... (código para ajustar fit e fit0)

# Criando os gráficos de diagnóstico
fig, axs = plt.subplots(2, 2, figsize=(10, 8))

# Gráficos para o modelo 'fit' (RLS)
sm.graphics.plot_regress_exog(fit, 'temp', fig=fig)

# Ajustando os títulos dos subplots
axs[0, 0].set_title("Resíduos vs. Valores Ajustados (RLS)")
axs[0, 1].set_title("Normal Q-Q (RLS)")
axs[1, 0].set_title("Scale-Location (RLS)")
axs[1, 1].set_title("Resíduos vs. Leverage (RLS)")

plt.tight_layout()
plt.show()

Exercício 7.8 Considerando o Exemplo 7.21, verifique:

  1. \(\hat{\beta}_0 = -19.110\).
  2. \(\hat{\beta}_1 = 5.915\).
  3. \(ep(\hat{\beta}_0) = 22.919\).
  4. \(ep(\hat{\beta}_1) = 0.674\).
  5. \(T_0=-0.83\).
  6. \(T_1=8.78\).
  7. O p-value associado à hipótese \(H_0:\beta_0=0\) é \(0.41\).
  8. O p-value associado à hipótese \(H_0:\beta_1=0\) é \(1.6e-09\).
  9. \(\hat{\beta}_1^{*} = 5.3590\).
  10. \(ep(\hat{\beta}_1^{*}) = 0.0973\).
  11. \(T_1^{*} = 55\).
  12. O p-value associado à hipótese \(H_0:\beta_1^{*}=0\) é \(<2e-16\).

Exercício 7.9 Considere novamente os dados do Exemplo 7.1.

  1. Realize o teste dos parâmetros do modelo descrito na Equação (7.13) considerando as Equações (7.19), (7.20), (7.21) e (7.22).
  2. Realize o teste dos parâmetros do modelo descrito na Equação (7.17) considerando as Equações (7.23) e (7.24).

7.2.3.6 Coeficiente de determinação

  • \(y_i = \text{realizado}\)
  • \(\hat{y}_i = \text{previsto (pelo modelo linear considerado)}\)
  • \(\bar{y} = \text{(previsto pela) média (incondicional) de } y\)

Coeficiente de determinação \[\begin{equation} r^2 = 1 - \frac{SQ_{res}}{SQ_{tot}} = 1 - \frac{\sum_{i=1}^n (y_i-\hat{y}_i)^2}{\sum_{i=1}^n (y_i-\bar{y})^2} \tag{7.27} \end{equation}\]

Coeficiente de determinação ajustado (Nagelkerke et al. 1991) \[\begin{equation} r_{a}^2 = 1 - \frac{SQ_{res}/gl_{res}}{SQ_{tot}/gl_{tot}} = 1 - \frac{(\sum_{i=1}^n (y_i-\hat{y}_i)^2)/(n-p)}{(\sum_{i=1}^n (y_i-\bar{y})^2)/(n-1)} = 1 - (1-r^2) \frac{n-1}{n-p-1} \tag{7.28} \end{equation}\]

onde \(n\) é o tamanho da amostra, \(p\) é o número de coeficientes estimados no modelo, \(gl_{res}=n-p-1\) são os graus de liberdade do resíduo e \(gl_{tot}=n-1\) são os graus de liberdade totais.

Pode-se colocar \(r_{a}^2\) em função de \(r^2\).

\[\begin{equation} r^2_{a} = 1 - (1-r^2) \frac{n-1}{n-p-1} \tag{7.29} \end{equation}\]

7.2.4 Diagnóstico preditivo

A análise preditiva consiste em avaliar a qualidade do modelo em relação à capacidade de predição de novos valores observados.

7.2.4.1 Erro Quadrático Médio

\[\begin{equation} MSE = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2 \tag{7.30} \end{equation}\]

7.2.4.2 Raiz do Erro Quadrático Médio

\[\begin{equation} RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2} \tag{7.31} \end{equation}\]

7.2.4.3 Desvio Absoluto Médio

\[\begin{equation} MAE = \frac{1}{n} \sum_{i=1}^n \left| \hat{y}_i - y_i \right| \tag{7.32} \end{equation}\]

7.2.4.4 Desvio Absoluto Médio Percentual

\[\begin{equation} MAPE = \frac{1}{n} \sum_{i=1}^n \left| \frac{\hat{y}_i - y_i}{y_i} \right| \tag{7.33} \end{equation}\]

7.2.4.5 Erro percentual médio simétrico absoluto

\[\begin{equation} SMAPE = \frac{1}{n} \sum_{i=1}^n \left(\frac{|\hat{y}_i - y_i|}{|\hat{y}_i| + |y_i|} \right) \tag{7.34} \end{equation}\]

Exemplo 7.27 Considere novamente os dados do Exemplo 7.1. Utilizando a ideia de treino-teste, pode-se comparar os modelos quanto às métricas de desempenho das Eqs. (7.30) a (7.34), implementadas na biblioteca DescTools (Signorell 2024).

Para isso são realizadas \(M=100\) replicações ajustando os modelos RLS e RPO com \(ntrain=20\) observações de treino, confrontadas com as \(ntest=10\) observações de teste restantes. Note que o sorteio da amostra é realizado através da função base::sample() associada a base::sed.seed() indexada por i, permitindo a replicação exata dos resultados.

library(DescTools)
M <- 100          # Número de repetições
ntrain <- 20      # Tamanho da amostra de treino
fit <- data.frame(MSE=NA, RMSE=NA, MAE=NA, MAPE=NA, SMAPE=NA)
fit0 <- data.frame(MSE=NA, RMSE=NA, MAE=NA, MAPE=NA, SMAPE=NA)

for(i in 1:M){
  set.seed(i); itrain <- sort(sample(1:nrow(dr), ntrain))
  train <- dr[itrain,]
  test <- dr[-itrain,]
  xtest <- data.frame(temp = dr[-itrain,'temp'])
  ytest <- test$gar
  fit_temp <- lm(gar ~ temp, data = train)
  fit0_temp <- lm(gar ~ temp-1, data = train)
  
  fit[i,'MSE'] <- DescTools::MSE(predict(fit_temp,xtest), ytest)
  fit[i,'RMSE'] <- DescTools::RMSE(predict(fit_temp,xtest), ytest)
  fit[i,'MAE'] <- DescTools::MAE(predict(fit_temp,xtest), ytest)
  fit[i,'MAPE'] <- DescTools::MAPE(predict(fit_temp,xtest), ytest)
  fit[i,'SMAPE'] <- DescTools::SMAPE(predict(fit_temp,xtest), ytest)
  
  fit0[i,'MSE'] <- DescTools::MSE(predict(fit0_temp,xtest), ytest)
  fit0[i,'RMSE'] <- DescTools::RMSE(predict(fit0_temp,xtest), ytest)
  fit0[i,'MAE'] <- DescTools::MAE(predict(fit0_temp,xtest), ytest)
  fit0[i,'MAPE'] <- DescTools::MAPE(predict(fit0_temp,xtest), ytest)
  fit0[i,'SMAPE'] <- DescTools::SMAPE(predict(fit0_temp,xtest), ytest)
}
# Tabelas
summary(fit)
##       MSE             RMSE            MAE             MAPE             SMAPE        
##  Min.   :145.9   Min.   :12.08   Min.   : 9.09   Min.   :0.05020   Min.   :0.05175  
##  1st Qu.:301.4   1st Qu.:17.36   1st Qu.:13.18   1st Qu.:0.07882   1st Qu.:0.07675  
##  Median :362.1   Median :19.03   Median :15.58   Median :0.09314   Median :0.09004  
##  Mean   :386.7   Mean   :19.38   Mean   :15.69   Mean   :0.09630   Mean   :0.09256  
##  3rd Qu.:455.0   3rd Qu.:21.33   3rd Qu.:17.74   3rd Qu.:0.11129   3rd Qu.:0.10599  
##  Max.   :815.2   Max.   :28.55   Max.   :23.90   Max.   :0.17260   Max.   :0.15168
summary(fit0)
##       MSE             RMSE            MAE              MAPE             SMAPE        
##  Min.   :137.8   Min.   :11.74   Min.   : 9.416   Min.   :0.05161   Min.   :0.05313  
##  1st Qu.:271.6   1st Qu.:16.48   1st Qu.:12.881   1st Qu.:0.07328   1st Qu.:0.07366  
##  Median :349.6   Median :18.70   Median :14.654   Median :0.08879   Median :0.08660  
##  Mean   :365.4   Mean   :18.80   Mean   :15.100   Mean   :0.09262   Mean   :0.08836  
##  3rd Qu.:453.6   3rd Qu.:21.30   3rd Qu.:17.413   3rd Qu.:0.10925   3rd Qu.:0.10261  
##  Max.   :779.3   Max.   :27.92   Max.   :23.279   Max.   :0.16734   Max.   :0.14754

Exemplo 7.28 Em Python.

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_error
import matplotlib.pyplot as plt

# Sample DataFrame 'dr' (replace with your actual data)
np.random.seed(0)
dr = pd.DataFrame({'gar': np.random.rand(50), 'temp': np.random.rand(50)})

M = 100
ntrain = 20

fit = pd.DataFrame(index=range(M), columns=['MSE', 'RMSE', 'MAE', 
                                            'MAPE', 'SMAPE'])
fit0 = pd.DataFrame(index=range(M), columns=['MSE', 'RMSE', 'MAE', 
                                             'MAPE', 'SMAPE'])

def smape(y_true, y_pred):
    numerator = np.abs(y_true - y_pred)
    denominator = (np.abs(y_true) + np.abs(y_pred)) / 2
    return np.mean(numerator / denominator) * 100

for i in range(M):
    np.random.seed(i + 1)
    itrain = np.sort(np.random.choice(dr.shape[0], ntrain, 
                     replace=False))
    train = dr.iloc[itrain]
    test = dr.drop(itrain)
    xtest = pd.DataFrame({'temp': test['temp']})
    ytest = test['gar'].values

    fit_temp = np.polyfit(train['temp'], train['gar'], 1)
    fit0_temp = np.polyfit(train['temp'], train['gar'], 1, 
                           full=True)[0]

    y_pred = np.poly1d(fit_temp)(xtest['temp'])
    y_pred0 = np.poly1d(fit0_temp)(xtest['temp'])

    fit.loc[i, 'MSE'] = mean_squared_error(ytest, y_pred)
    fit.loc[i, 'RMSE'] = np.sqrt(fit.loc[i, 'MSE'])
    fit.loc[i, 'MAE'] = mean_absolute_error(ytest, y_pred)
    fit.loc[i, 'MAPE'] = np.mean(np.abs((ytest-y_pred)/ytest))*100
    fit.loc[i, 'SMAPE'] = smape(ytest, y_pred)

    fit0.loc[i, 'MSE'] = mean_squared_error(ytest, y_pred0)
    fit0.loc[i, 'RMSE'] = np.sqrt(fit0.loc[i, 'MSE'])
    fit0.loc[i, 'MAE'] = mean_absolute_error(ytest, y_pred0)
    fit0.loc[i, 'MAPE'] = np.mean(np.abs((ytest-y_pred0)/ytest))*100
    fit0.loc[i, 'SMAPE'] = smape(ytest, y_pred0)

print(fit.describe())
print(fit0.describe())

References

Akaike, Hirotugu. 1974. “A New Look at the Statistical Model Identification.” In Selected Papers of Hirotugu Akaike, 215–22. Springer. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=1100705.
Cook, R Dennis. 1977. “Detection of Influential Observation in Linear Regression.” Technometrics 19 (1): 15–18. http://www.stat.ucla.edu/~nchristo/statistics100C/1268249.pdf.
DeGroot, Morris H, and Mark J Schervish. 2012. Probability and Statistics. Pearson Education.
Eisenhauer, Joseph G. 2003. “Regression Through the Origin.” Teaching Statistics 25 (3): 76–80. https://doi.org/10.1111/1467-9639.00136.
Galton, Francis. 1889. Natural Inheritance. Macmillan; Company. https://archive.org/details/in.ernet.dli.2015.221860.
Nagelkerke, Nico JD et al. 1991. “A Note on a General Definition of the Coefficient of Determination.” Biometrika 78 (3): 691–92. https://www.cesarzamudio.com/uploads/1/7/9/1/17916581/nagelkerke_n.j.d._1991_-_a_note_on_a_general_definition_of_the_coefficient_of_determination.pdf.
Paula, Gilberto Alvarenga. 2024. Modelos de Regressão: Com Apoio Computacional. IME-USP São Paulo. https://www.ime.usp.br/~giapaula/texto_2024.pdf.
Schwarz, Gideon. 1978. “Estimating the Dimension of a Model.” The Annals of Statistics, 461–64. https://doi.org/10.1214/aos/1176344136.
Signorell, Andri. 2024. DescTools: Tools for Descriptive Statistics. https://CRAN.R-project.org/package=DescTools.
———. 1997. “Regression Towards the Mean, Historically Considered.” Statistical Methods in Medical Research 6 (2): 103–14. https://doi.org/10.1177/096228029700600202.
Yule, G. Udny, and Maurice G. Kendall. 1948. Introdução à Teoria Da Estatı́stica. Translated by Evandro de Oliveira Silva. 13th ed. IBGE - Instituto Brasileiro de Geografia e Estatı́stica.

  1. Qualitatively both our procedure and Akaike’s give “a mathematical formulation of the principle of parsimony in model building.” Quantitatively, since our procedure differs from Akaike’s only in that the dimension is multiplied by \(\frac{1}{2}\log n\), our procedure leans more than Akaike’s towards lower-dimensional models (when there are 8 or more observations). For large numbers of observations the procedures differ markedly from each other. If the assumptions we made in Section 2 are accepted, Akaike’s criterion cannot be asymptotically optimal. This would contradict any proof of its optimality, but no such proof seems to have been published, and the heuristics of Akaike [1] and of Tong [4] do not seem to lead to any such proof.↩︎