5.7 Estimação Pontual
Na estimação pontual utiliza-se uma estatística, calculada a partir de um estimador como estimativa (pontual) de um certo parâmetro, conforme Definições 5.13 e 5.14. Em outras palavras, é utilizado um único valor (ponto) para estimar \(\theta\), simbolizado por \(\hat{\theta}\) e lido como teta chapéu. Sob o prisma da Teoria da Decisão, um estimador é chamado regra de decisão (Berger 1985, 9).
Definição 5.13 Um estimador \(\hat{\theta}(\boldsymbol{x}) \equiv \hat{\theta}\) é uma função que tem por objetivo inferir sobre um parâmetro \(\theta(\boldsymbol{X}) \equiv \theta\).
Definição 5.14 Uma estimativa é um particular valor obtido da aplicação dos dados amostrais em um estimador.
Na inferência bayesiana costuma-se trabalhar com uma das seguintes medidas como estimadores pontuais.
Exemplo 5.30 Considerando os dados do Exemplo 5.6 e uma priori \(Beta(1,1)\), pode-se calcular as estimativas pontuais da posteriori \(Beta(10,4)\) pelas Equações (3.97), (3.99) e (3.100).
# \theta ~ Beta(1,1), \theta|x ~ Beta(1+s,1+f)
s <- 9
f <- 3
(EX = (s+1)/(s+1+f+1)) # Média a posteriori (vermelho)## [1] 0.7142857## [1] 0.725## [1] 0.75curve(dbeta(x, s+1,f+1))
abline(v = EX, col = 'red')
abline(v = MEX, col = 'blue')
abline(v = MOX, col = 'green')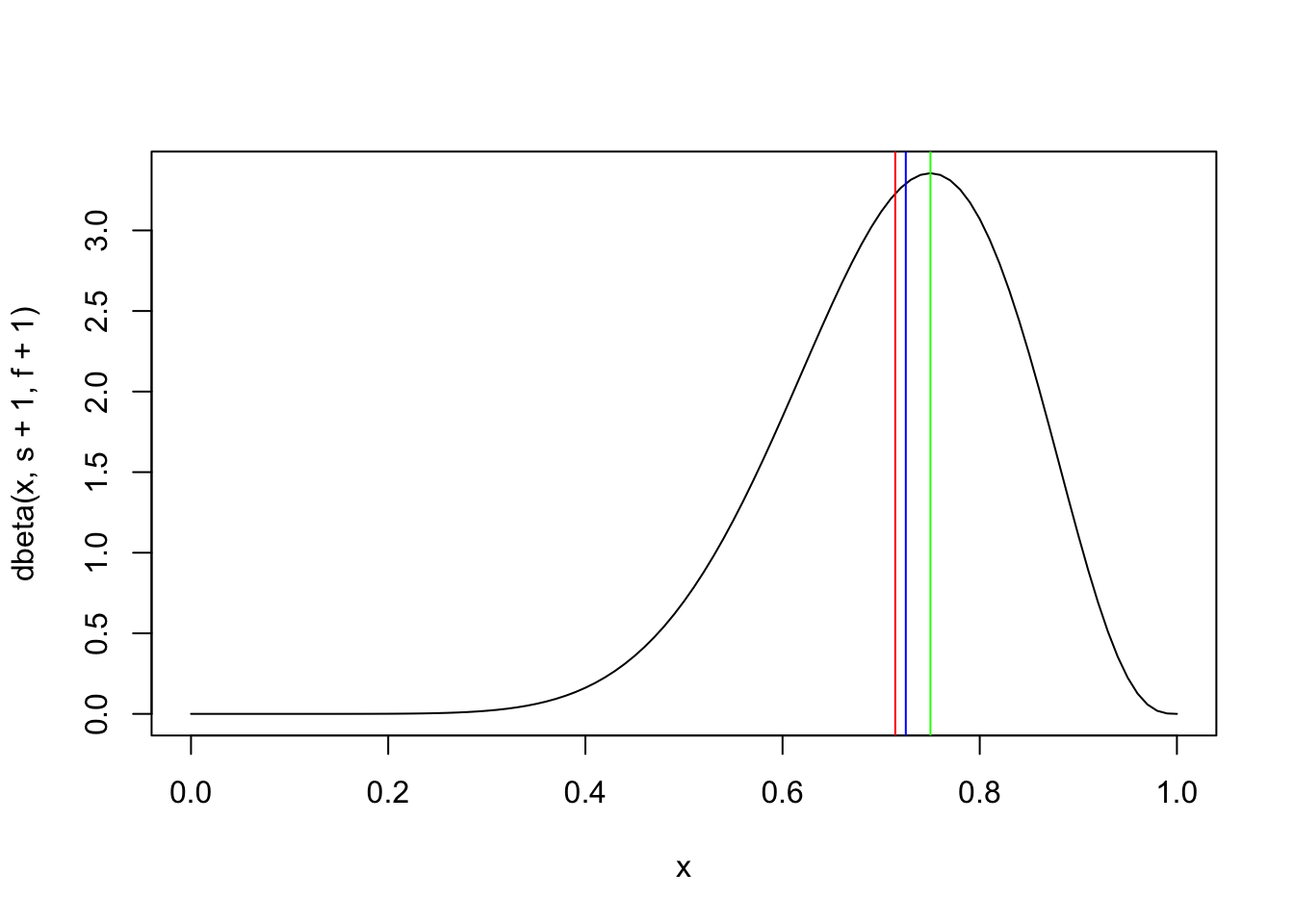
Exemplo 5.31 Em Python.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Parâmetros da distribuição Beta
s = 9 # Número de sucessos
f = 3 # Número de fracassos
# Calculando a média, mediana e moda da posteriori
EX = (s + 1) / (s + 1 + f + 1) # Média
MEX = (s + 1 - 1/3) / (s + 1 + f + 1 - 2/3) # Mediana
MOX = (s + 1 - 1) / (s + 1 + f + 1 - 2) # Moda
# Plotando a curva da densidade Beta
x = np.linspace(0, 1, 100)
plt.plot(x, beta.pdf(x, s + 1, f + 1), label='Beta(10, 4)')
# Adicionando linhas verticais para a média, mediana e moda
plt.axvline(x=EX, color='red', linestyle='--', label='Média')
plt.axvline(x=MEX, color='blue', linestyle='--', label='Mediana')
plt.axvline(x=MOX, color='green', linestyle='--', label='Moda')
plt.xlabel(r'$\theta$')
plt.ylabel('Densidade')
plt.title(r'Distribuição Beta($\theta$|x)')
plt.legend()
plt.show()
# Imprimindo os valores da média, mediana e moda
print(f"Média (EX): {EX:.4f}") # Output: 0.7143
print(f"Mediana (MEX): {MEX:.4f}") # Output: 0.7317
print(f"Moda (MOX): {MOX:.4f}") # Output: 0.8000Exercício 5.24 Veja
- Seção 3.2 de (Paulino, Turkman, and Murteira 2003)
- Seções 8.2 e 8.3 de (S. J. Press 2003)