5.6 Simulação
It’s like a rolling dice / It goes 1, 2, 3, 4 times / Randomly accurate / It feels chaotic (right?) (Far From Alaska 2014)
Exercício 5.9 Veja os vídeos do canal Primer.
5.6.1 Monte Carlo
(Metropolis and Ulam 1949) propuseram o chamado método de Monte Carlo, em alusão ao complexo de cassinos em Monte Carlo na Itália. A proposta “consiste em uma mistura de processos determinísticos e estocásticos” ao considerar extrações “de forma aleatória e independente” admitindo “duas classes: (1) produção de valores ‘aleatórios’ com sua distribuição de frequência igual àquelas que regem a mudança de cada parâmetro, (2) cálculo dos valores daqueles parâmetros que são determinísticos, ou seja, obtidos algebricamente dos demais”.
It may seem strange that the machine can simulate the production of a series of random numbers, but this is indeed possible. In fact, it suffices to produce a sequence of numbers between 0 and 1 which have a uniform distribution in this interval but otherwise are uncorrelated, i.e., pairs will have uniform distribution in the unit square, triplets uniformly distributed in the unit cube, etc., as far as practically feasible. (Metropolis and Ulam 1949, 339)
Exemplo 5.15 A função stats::runif() gera uniformes no R. Está configurada pra gerar uniformes padrão, anotado por \(\mathcal{U}(0,1)\) conforme Seção 3.9.1.
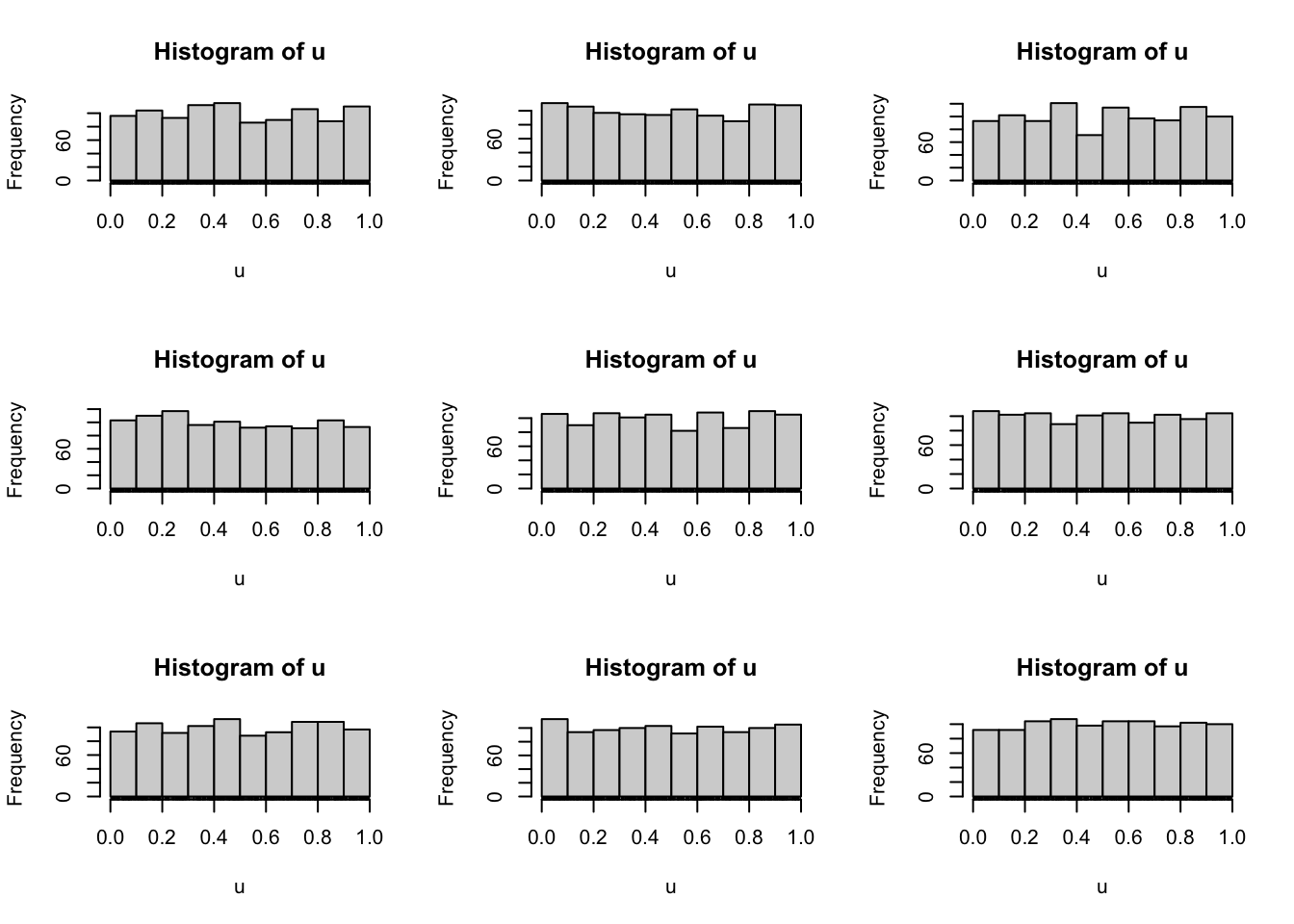
Exemplo 5.16 Em Python.
import numpy as np
import matplotlib.pyplot as plt
# Criando a figura com 3x3 subplots
fig, axs = plt.subplots(3, 3, figsize=(10, 8))
# Loop para gerar os histogramas
for i in range(1, 10):
np.random.seed(i)
u = np.random.rand(1000)
# Calculando a posição do subplot
row = (i - 1) // 3
col = (i - 1) % 3
# Plotando o histograma
axs[row, col].hist(u, density=True, bins='auto',
color='lightgray', edgecolor='black')
axs[row, col].set_title(f'Semente: {i}')
axs[row, col].set_xlabel('Valores')
axs[row, col].set_ylabel('Densidade')
# Adicionando o "rug plot" (opcional)
# sns.rugplot(u, ax=axs[row, col], color='black')
plt.tight_layout()
plt.show()Exercício 5.10 Veja a documentação de base::set.seed().
Exercício 5.11 Veja o Capítulo 6 de (Peng 2022).
5.6.1.1 Geração de variáveis aleatórias discretas
(Gamerman and Lopes 2006) sugerem procedimentos bastante simples para gerar valores das principais distribuições discretas a partir de valores de uma \(\mathcal{U}(0,1)\).
Distribuição Bernoulli
É possível gerar \(M\) valores de uma Bernoulli de parâmetro \(\theta\) da seguinte forma:
- Obtenha \(u\) de uma \(\mathcal{U}(0,1)\).
- Se \(u \le \theta\) faça \(x=1\), caso contrário \(x=0\).
- Repita 1 e 2 \(M\) vezes.
Exemplo 5.17 Deseja-se gerar \(M=1000\) observações de uma Bernoulli de parâmetro \(\theta=0.75\).
# parâmetros
M <- 1000
theta <- 0.75
x <- vector(length = M)
# loop
for(i in 1:M){
# passo 1
set.seed(3*i); u <- runif(1)
# passo 2
x[i] <- as.numeric(u <= theta)
}
# verificando
tab <- table(x)
(ptab <- prop.table(tab))## x
## 0 1
## 0.228 0.772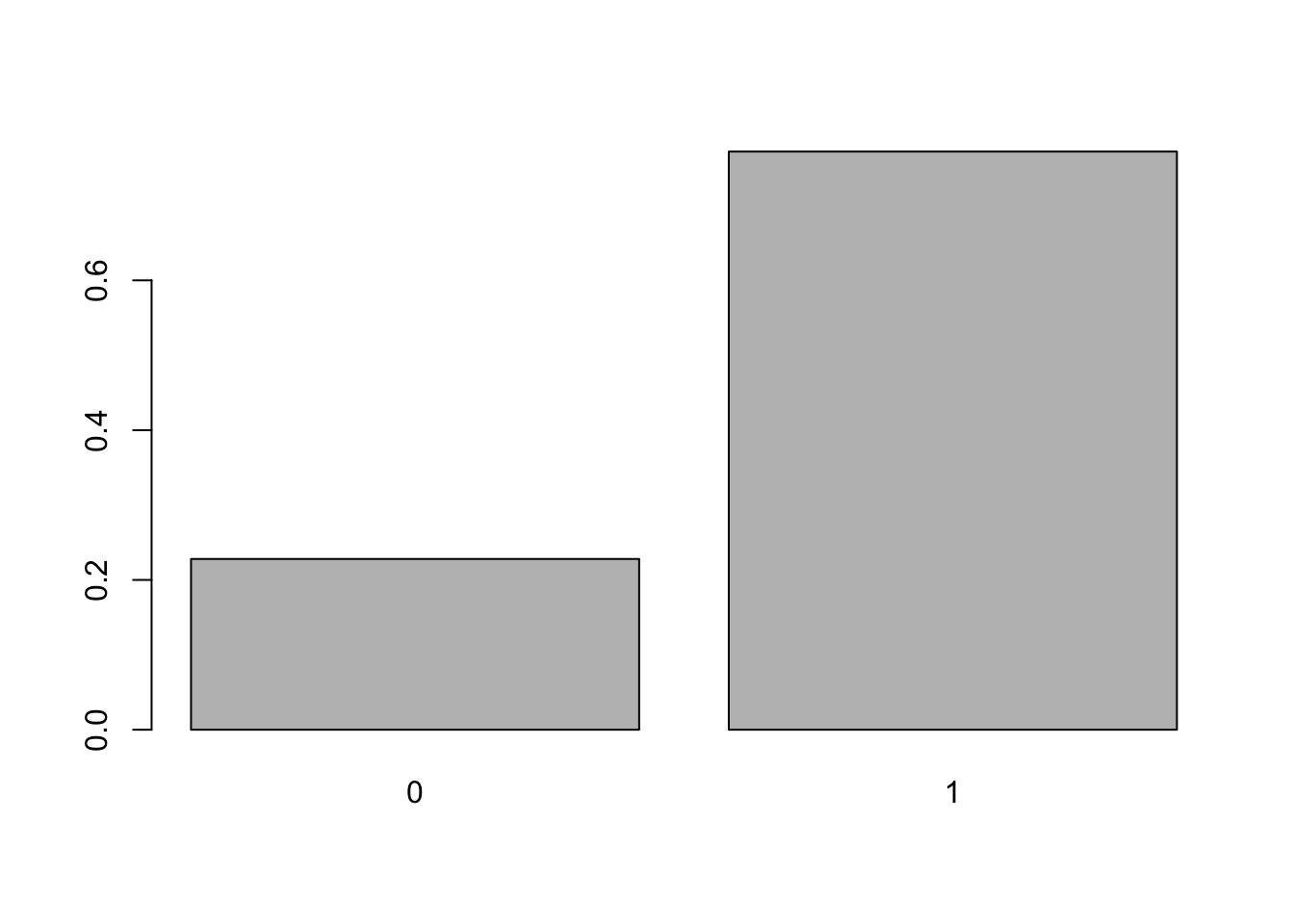
Exemplo 5.18 Em Python.
import numpy as np
# Parâmetros
M = 1000
theta = 0.75
x = np.zeros(M)
# Loop
for i in range(M):
# Passo 1
np.random.seed(3 * i)
u = np.random.rand()
# Passo 2
x[i] = int(u <= theta)
# Verificando
unique, counts = np.unique(x, return_counts=True)
tab = dict(zip(unique, counts))
ptab = counts / M
print(tab)
print(ptab)Distribuição Binomial
É possível gerar \(M\) valores \(x\) de uma Binomial de parâmetros \(n\) e \(\theta\) da seguinte forma:
- Obtenha \(u_1,u_2,\ldots,u_n\), todos de uma \(\mathcal{U}(0,1)\).
- Se \(u_i \le \theta\) faça \(x_i=1\), caso contrário \(x_i=0\). Obtenha \(\sum_{i=1}^{n} x_i\).
- Repita 1 e 2 \(M\) vezes.
Exemplo 5.19 Deseja-se gerar \(M=1000\) observações de uma Binomial de parâmetros \(n=10\) e \(\theta=0.75\).
# parâmetros
M <- 1000
n <- 10
theta <- 0.75
x <- vector(length = M)
# loop
for(i in 1:M){
# passo 1
set.seed(i+314); u <- runif(n)
# passo 2
x[i] <- sum(u < theta)
}
# verificando
tab <- table(x)
(ptab <- prop.table(tab))## x
## 3 4 5 6 7 8 9 10
## 0.001 0.018 0.066 0.136 0.258 0.284 0.177 0.060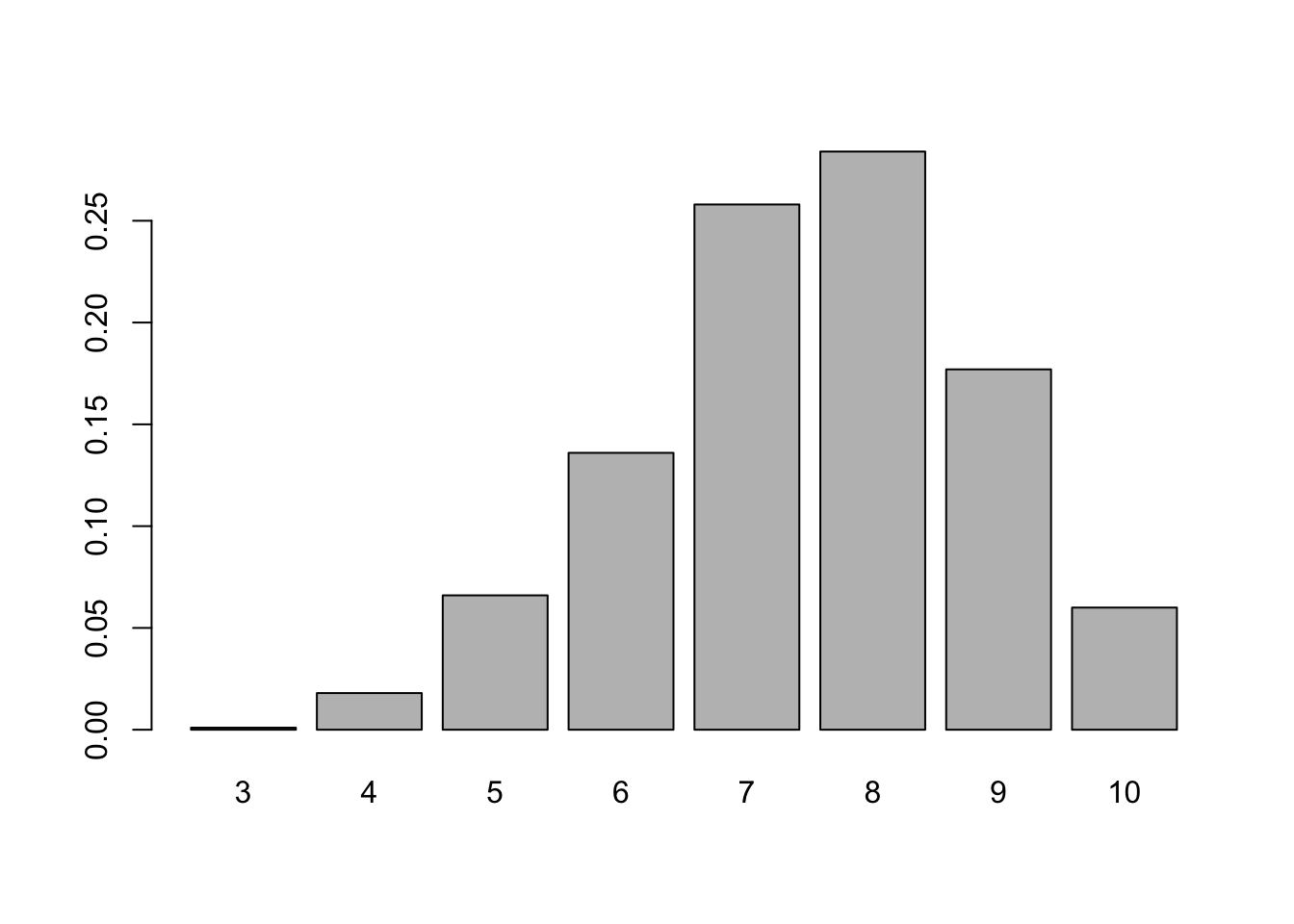
## [1] 9.536743e-07 2.861023e-05 3.862381e-04 3.089905e-03 1.622200e-02 5.839920e-02 1.459980e-01 2.502823e-01
## [9] 2.815676e-01 1.877117e-01 5.631351e-02Exemplo 5.20 Em Python.
import numpy as np
# Parâmetros
M = 1000
n = 10
theta = 0.75
x = np.zeros(M)
# Loop
for i in range(M):
# Passo 1
np.random.seed(i + 314)
u = np.random.rand(n)
# Passo 2
x[i] = np.sum(u < theta)
# Verificando
unique, counts = np.unique(x, return_counts=True)
tab = dict(zip(unique, counts))
ptab = counts / M
print(tab)
print(ptab)Exercício 5.12 Considere os Exemplos 5.17 e 5.19.
- Compare os resultados com aqueles obtidos por
stats::rbinom(). Considere funções comoplot(ecdf(x)),fisher.test()eks.test(). - Repita o procedimento no Python usando
np.random.binomial(). - Use uma tabela de dígitos aleatórios para simular \(M=5\) observações de cada exemplo.
5.6.1.2 Método da Transformação Inversa
Pode-se obter uma amostra de tamanho \(M\) de uma densidade \(f\) e acumulada \(F(x) = \int_{-\infty}^{x} f(t) dt\) da seguinte maneira:
- Obtenha \(u\) de uma \(\mathcal{U}(0,1)\).
- Calcule \(F^{-1}(u)\).
- Repita 1 e 2 \(M\) vezes.
Exercício 5.13 Veja o artigo Inverse transform sampling.

Exemplo 5.21 Considere a distribuição exponencial tal que \(F(x|\lambda) = 1 - e^{-\lambda x}\). A inversa de \(F\) é
\[\begin{equation} F^{-1}(u|\lambda) = -\frac{\log(1-u)}{\lambda} \tag{5.7} \end{equation}\]
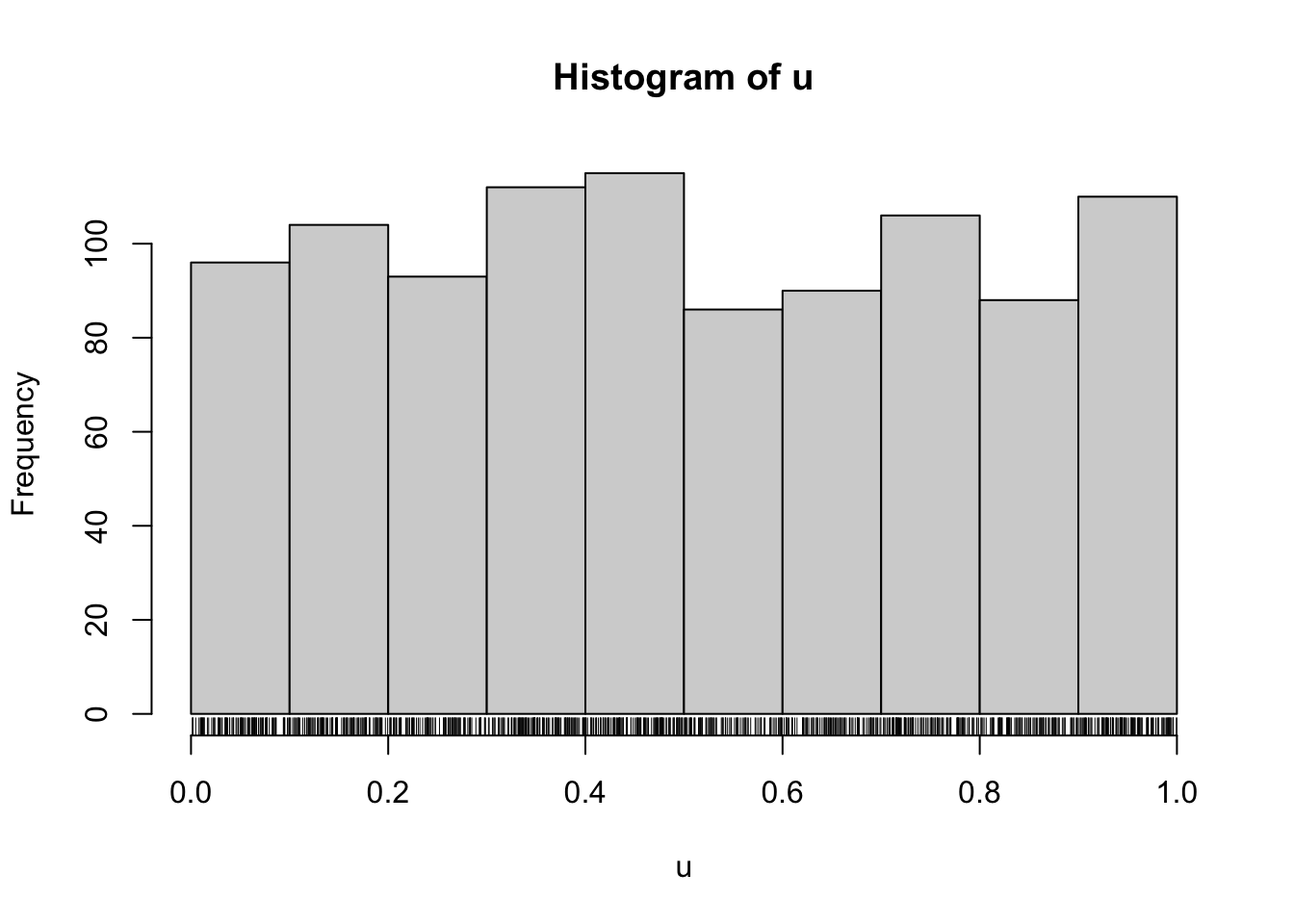
# Passo 2: exponencial de taxa 3
lambda <- 3
x <- -log(1-u)/lambda
hist(x, 40, probability = TRUE); rug(x)
curve(dexp(x,3), add = TRUE, col = 'red')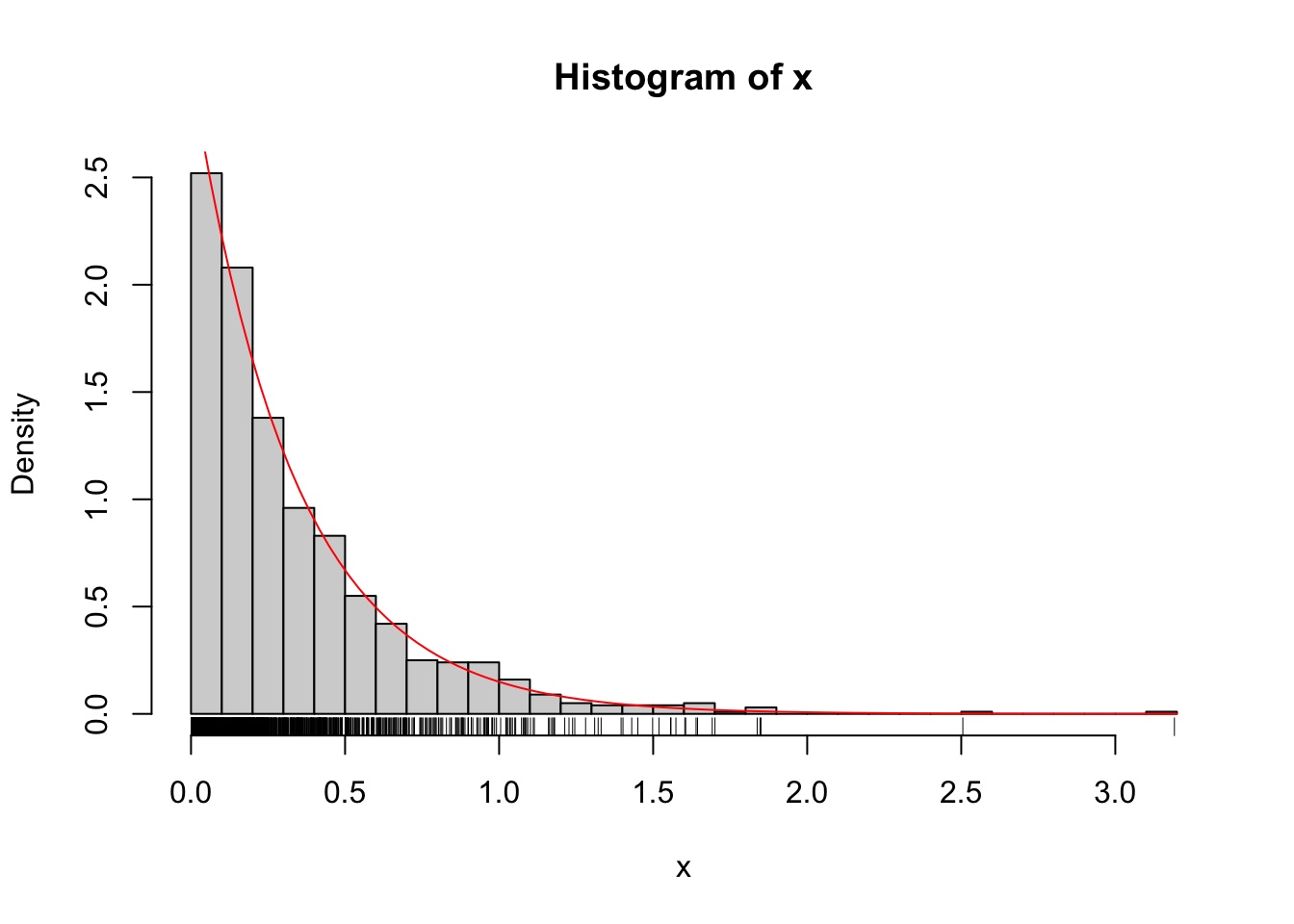
## [1] 0.3333333## [1] 0.3373056## [1] 0.1111111## [1] 0.1208113## [1] 0.7768698## [1] 0.7768698## [1] 0.777Exemplo 5.22 Em Python.
import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt
# Passo 1: uniforme em [0,1]
M = 1000
np.random.seed(1)
u = np.random.rand(M)
plt.hist(u, bins='auto', density=True, color='lightgray',
edgecolor='black')
plt.title('Distribuição Uniforme (0, 1)')
plt.xlabel('Valores')
plt.ylabel('Densidade')
# plt.rugplot(u, color='black') # Rug plot (opcional)
plt.show()
# Passo 2: exponencial de taxa 3
lambda_ = 3
x = -np.log(1 - u) / lambda_
plt.hist(x, bins=30, density=True, color='lightgray',
edgecolor='black')
plt.title('Distribuição Exponencial (taxa = 3)')
plt.xlabel('Valores')
plt.ylabel('Densidade')
# plt.rugplot(x, color='black') # Rug plot (opcional)
# Curva da densidade exponencial teórica
x_range = np.linspace(x.min(), x.max(), 100)
plt.plot(x_range, expon.pdf(x_range, scale=1/lambda_),color='red')
plt.show()
# Média teórica
media_teorica = 1 / lambda_
print(f"Média teórica: {media_teorica:.4f}")
# Média empírica
media_empirica = np.mean(x)
print(f"Média empírica: {media_empirica:.4f}")
# Variância teórica
variancia_teorica = 1 / lambda_**2
print(f"Variância teórica: {variancia_teorica:.4f}")
# Variância empírica
variancia_empirica = np.var(x)
print(f"Variância empírica: {variancia_empirica:.4f}")
# P(X<0.5) teórica
prob_teorica = 1 - np.exp(-lambda_ * 0.5)
print(f"P(X<0.5) teórica: {prob_teorica:.4f}")
# P(X<0.5) usando scipy.stats.expon
prob_scipy = expon.cdf(0.5, scale=1/lambda_)
print(f"P(X<0.5) (scipy): {prob_scipy:.4f}")
# P(X<0.5) empírica
prob_empirica = np.sum(x < 0.5) / M
print(f"P(X<0.5) empírica: {prob_empirica:.4f}")Exercício 5.14 Mostre que a inversa da FDA da exponencial pode ser dada pela Equação (5.7).
Exercício 5.15 Considere a distribuição triangular apresentada na Seção 3.9.9.
- Mostre que \(F^{-1}(u)\) é dada conforme a Eq. (3.113).
- Simule a densidade de uma \(\mathcal{Tri}(0,0.6,1)\) a partir do Método da Transformação Inversa.
- Compare com os resultados de
extraDistr::rtriang()do R enp.random.triangular()do Python. - Calcule \(P(X>0.37)\) via simulação e compare com a probabilidade teórica.
Exercício 5.16 Sabe-se que se a variável \(U\) tem distribuição uniforme no intervalo (0,1), então \(X=\sigma \sqrt{-2 \log U}\) tem distribuição Rayleigh de parâmetro \(\sigma\). Realizando a transformação de variáveis, obtém-se \(f(x|\sigma)=\frac{x}{\sigma^2}e^{-x^2/(2\sigma^2)}\) e \(F(x|\sigma)=1-e^{-x^2/(2\sigma^2)}\).
- Obtenha \(F^{-1}(u)\).
- Simule a densidade de uma \(\mathcal{Rayleigh}(1)\) a partir do Método da Transformação Inversa.
- Compare com os resultados de
extraDistr::drayleigh()do R ounp.random.rayleigh()do Pyhon. - Calcule \(P(X<0.5)\) via simulação e compare com a probabilidade teórica.
5.6.1.3 Amostragem com rejeição
Pode-se obter uma amostra de uma densidade \(f\) a partir de uma função \(g\) de fácil obtenção da seguinte maneira:
- Obtenha \(u\) de uma \(\mathcal{U}(0,1)\).
- Obtenha um candidato \(x\) com distribuição \(g\).
- Se \(u \le \frac{f(x)}{k\,g(x)}\) admite-se o candidato \(x\), caso contrário rejeita-se \(x\).
- Repita 1 a 3 \(M\) vezes.
(Albert 2009, 117) aponta que “[a] amostragem por rejeição é um método geral para simular a partir de uma distribuição posteriori arbitrária, mas pode ser difícil de ser estabelecida, pois requer a construção de uma densidade de proposta [\(g(x)\)] adequada35.”
Exemplo 5.23 Adaptado da Seção 6.3 de (Peng 2022). Deseja-se amostrar de uma exponencial com \(\lambda=1\). Para isso considera-se \(U \sim \mathcal{U}(0,10)\) e constante \(k=10\).
A seguir podem-se considerar os gráficos e as simulações.
# gráficos analíticos
curve(dexp(x, 1), 0, 10, col = 4, ylab = 'Densidade')
segments(0, 1, 10, 1, col = 1)
# elementos da simulação
fdist <- vector()
lambda <- 1
g <- 1/10
k <- 10
M <- 1000
j <- 0
# loop
for(i in 1:M){
# Passo 1: Simular U ~ Unif(0,1)
set.seed(i); (U <- runif(1, 0, 1))
# Passo 2: Simular um candidato X ~ g, i.e., X ~ Unif(0,10)
set.seed(i+1); (X <- runif(1, 0, 10))
# Apresentando X no gráfico
rug(X)
# Avaliando f no ponto candidato X
f <- lambda*exp(-lambda*X)
# Passo 3: decidindo se o candidato entra ou não na amostra
# Se U > f/(k*g) indicar com um x vermelho, X não entra como ponto de f
if(U > f/(k*g)){
points(X, U, pch = 'x', col = 'red')
}
# Se U <= f/(k*g)), indicar com um x verde, X entra como ponto de f
if(U <= f/(k*g)){
points(X, U, pch = 'x', col = 'green')
j <- j+1
fdist[j] <- X
}
}
# legenda
legend('right', c('10*g(x) U(0,10)', 'f(x) Exp(1)'), lty = 1,
col = c(1, 4), box.col = 'white')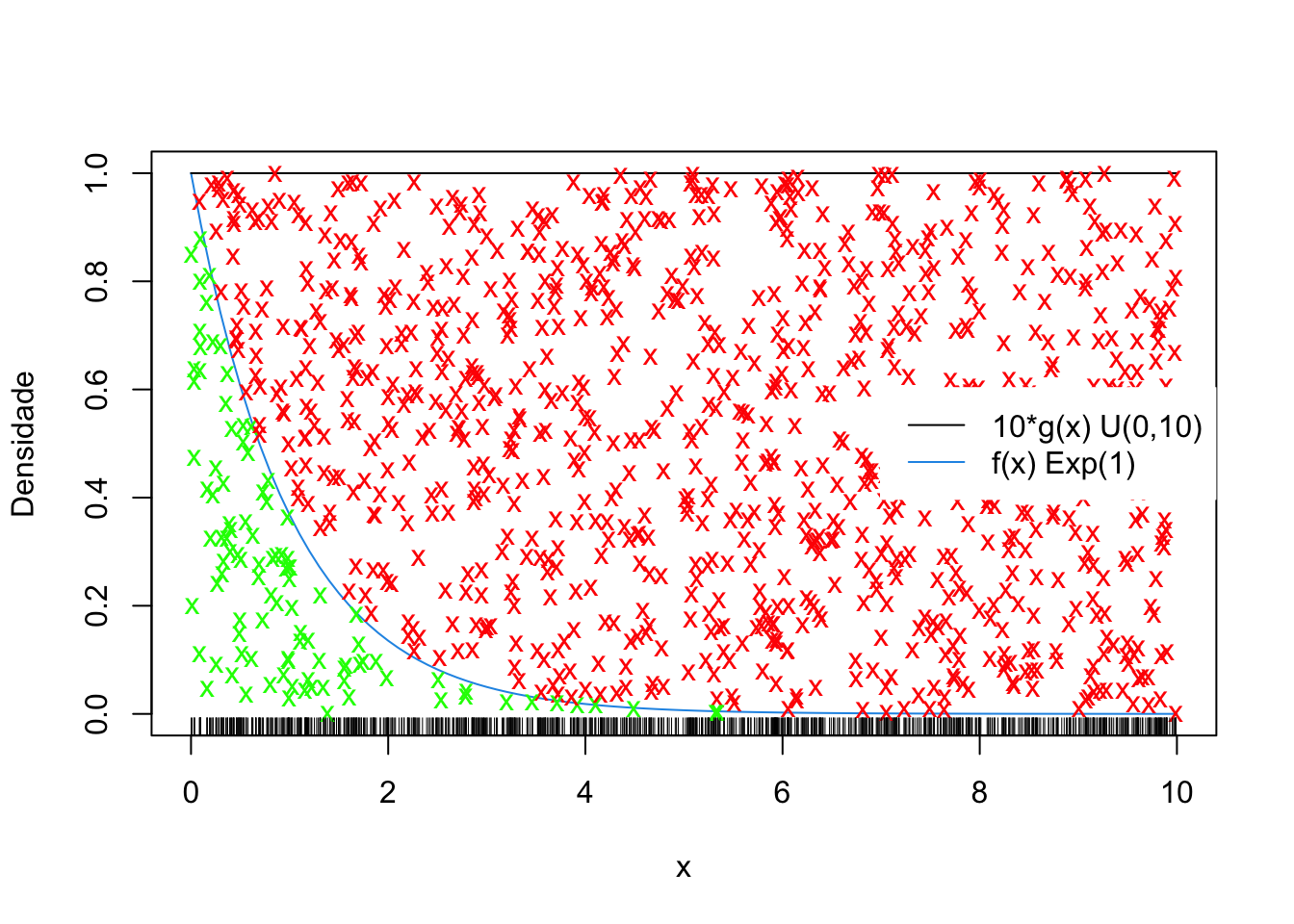
Note que o tamanho de fdist é 103, o que representa apenas 10.3% dos 1000 valores simulados, indicando um algoritmo pouco eficiente. Pode-se utilizar a simulação para calcular probabilidades, tal como \(P(X<1)\). Por se tratar de uma conhecida distribuição exponencial, pode-se comparar o valor estimado com o valor obtido analiticamente.
## [1] 0.6601942## [1] 0.6321206## [1] 0.6321206Exemplo 5.24 Em Python.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon
# Parâmetros
M = 1000
lambda_ = 1
g = 1/10
k = 10
fdist = []
# Gráfico da densidade exponencial
x_range = np.linspace(0, 10, 100)
plt.plot(x_range, expon.pdf(x_range, scale=1/lambda_),
color='blue', label='f(x) Exp(1)')
plt.hlines(1, 0, 10, color='black',
label='10*g(x) U(0,10)') # Linha horizontal para 10g(x)
# Loop para gerar os pontos
for i in range(1, M + 1):
# Passo 1: Simular U ~ U(0,1)
np.random.seed(i)
U = np.random.rand()
# Passo 2: Simular um candidato X ~ g, i.e., X ~ U(0,10)
np.random.seed(i + 1)
X = np.random.uniform(0, 10)
# Avaliando f no ponto candidato X
f = lambda_ * np.exp(-lambda_ * X)
# Passo 3: decidindo se o candidato entra ou não na amostra
if U > f / (k * g):
plt.plot(X, U, 'x', color='red')
else:
plt.plot(X, U, 'x', color='green')
fdist.append(X)
# Adicionando rug plot (opcional)
# plt.rugplot(np.array(fdist), color='green', label='Amostra')
# Configurações do gráfico
plt.xlabel('x')
plt.ylabel('Densidade')
plt.title('Simulação de Monte Carlo - Rejeição')
plt.legend()
plt.show()5.6.2 MCMC
Os métodos de Monte Carlo via Cadeia de Markov (Markov Chain Monte Carlo ou MCMC) foram popularizados por (Gelfand and Smith 1990), quando “apontaram com sucesso para a comunidade estatística em geral que o esquema de amostragem desenvolvido por (Geman and Geman 1984) para distribuições de Gibbs poderia de fato ser usado para uma série de outras distribuições posterioris” (Gamerman and Lopes 2006, 141)36.
Apesar de (Hastings 1970) ter generalizado o algoritmo de (Metropolis et al. 1953) – o que ficou conhecido como algoritmo de Metropolis-Hastings –, (Pettitt and Hincksman 2013) indicam que “a ideia permaneceu sem uso na literatura estatística”. Os autores apontam que as abordagens MCMC possuem “uma clara conexão entre o algoritmo de maximização da expectativa (EM) (…) e a amostragem de Gibbs” e “foram desenvolvidas para modelos onde há variáveis latentes usadas na verossimilhança, como modelos mistos, modelos de mistura e modelos para processos estocásticos”.
Para detalhes dos métodos, veja o Capítulo 7 de (Peng 2022).
5.6.2.1 Cadeia de Markov
A popular model for systems that change over time in a random manner is the Markov chain model. A Markov chain is a sequence of random variables, one for each time. At each time, the corresponding random variable gives the state of the system. Also, the conditional distribution of each future state given the past states and the present state depends only on the present state. (DeGroot and Schervish 2012, 188)
Exemplo 5.25 Suponha que clientes sejam classificados nas categorias A, B e C. Pode-se observar a migração entre essas classes no tempo, gerando uma matriz estocástica \(P\).
P <- matrix(c(.7,.2,.1, .1,.6,.3, 0,.1,.9),
nrow = 3, byrow = TRUE)
rownames(P) <- colnames(P) <- LETTERS[1:nrow(P)]
P## A B C
## A 0.7 0.2 0.1
## B 0.1 0.6 0.3
## C 0.0 0.1 0.9Os valores indicam probabilidades condicionais em um passo conforme Seção 3.4. Por exemplo,
\[P(A_{t+1}|A_{t})=p_{AA}^{1}=0.7, \;\;\; P(C_{t+1}|B_{t})=p_{BC}^{1}=0.3, \;\;\; P(A_{t+1}|C_t)=p_{CA}^{1}=0.0 \]
É possível obter as probabilidades de transição em \(k\) passos, bastando multiplicar \(P\) por ela mesma \(k\) vezes. No que a notação %*% indica uma multiplicação matricial no R.
## A B C
## A 0.51 0.27 0.22
## B 0.13 0.41 0.46
## C 0.01 0.15 0.84Por exemplo, \[P(A_{t+2}|A_{t})=p_{AA}^{2}=0.51, \; P(C_{t+2}|B_{t})=p_{BC}^{2}=0.46, \; P(A_{t+2}|C_t)=p_{CA}^{2}=0.01 \]
Note que \[\begin{align*} P(A_{t+2}|A_{t}) =& P(A_{t+2}|A_{t+1},A_{t}) + P(A_{t+2}|B_{t+1},A_{t}) + P(A_{t+2}|C_{t+1},A_{t}) \\ =& 0.7 \times 0.7 + 0.2 \times 0.1 + 0.1 \times 0.0 \\ P(A_{t+2}|A_{t}) =& 0.51 \end{align*}\]
## A B C
## A 0.384 0.286 0.330
## B 0.132 0.318 0.550
## C 0.022 0.176 0.802Por exemplo, \[P(A_{t+3}|A_{t})=p_{AA}^{3}=0.384, \; P(C_{t+2}|B_{t})=p_{BC}^{3}=0.550, \; P(A_{t+2}|C_t)=p_{CA}^{3}=0.022 \]
Exercício 5.17 Considere o Exemplo 5.25.
- Escreva todas as probabilidades condicionais em um passo (associadas a \(P\)).
- Verifique que \(P \times P \times P = P \times P2 = P2 \times P\).
- Escreva todas as probabilidades condicionais em dois passos (associadas a \(P2\)), realizando os cálculos intermediários e conferindo os valores.
- Verifique que as linhas das matrizes \(P\), \(P2\) e \(P3\) somam 1.
- Crie a matriz \(P\) e calcule \(P2\) e \(P3\) em Pyhton.
- Escreva uma função que tenha como entrada a matriz \(P\) e o número de passos desejados \(k\), que devolva \(Pk\) e verifique que a soma das linhas é 1.
Exercício 5.18 Assita o vídeo The Strange Math That Predicts (Almost) Anything do canal Veritasiun.
Exemplo 5.26 Considere os dados do Exemplo 5.25. Se no tempo \(t=0\) há 324 clientes na categoria A, 233 na B e 210 na C, pode-se simular o valor esperado de clientes em cada categoria ao longo do tempo.
P <- matrix(c(.7,.2,.1, .1,.6,.3, 0,.1,.9),
nrow = 3, byrow = TRUE)
rownames(P) <- colnames(P) <- LETTERS[1:nrow(P)]
(v0 <- c(324,233,210)) # t=0## [1] 324 233 210## A B C
## [1,] 250.1 225.6 291.3## A B C
## [1,] 197.63 214.51 354.86Definições
Definição 5.5 Um estado \(A\) é absorvente se e somente se \(p_{A,A}^{1}=1\), i.e., uma vez atingido o estado \(A\), nele se fica.
Definição 5.6 Uma classe \(S\) de estados é fechada se e somente se \(p_{S,S}^{1}=1\), i.e., uma vez atingida a classe \(S\), nela se fica.
Definição 5.7 Uma cadeia de Markov \(M\) é irredutível se e somente se \(p_{ij}^{k}>0 \; \forall i,j \in M\), i.e., quando todos os estados se comunicam, ainda que em mais de um passo.
Definição 5.8 \(T^{A \rightarrow A} = \text{MDC}\{n: \; p_{A_{n}|A_{0}}^{k}>0\}, \; \forall k \in \{1,2,\ldots\}\), i.e., \(T^{A \rightarrow A}\) é o número de passos (períodos) para voltar ao estado \(A\) dado que a cadeia inicia em \(A\).
Definição 5.9 Um estado \(A\) é recorrente se e somente se \(P(T^{A \rightarrow A} = \infty) = 0\), i.e., garante-se que \(A\) pode ser visitado infinitamente.
Definição 5.10 Um estado \(A\) é transiente se e somente se \(P(T^{A \rightarrow A} = \infty) > 0\), i.e., existe uma probabilidade maior que zero de que \(A\) nunca mais seja visitado.
Definição 5.11 Uma cadeia da Markov é aperiódica se e somente se \(T^{A \rightarrow A} = 1\), e periódica se e somente se \(T^{A \rightarrow A} > 1\).
Exercício 5.19
- Verifique que \(P(T^{A \rightarrow A} = \infty) = 0 \equiv P(T^{A \rightarrow A} < \infty) = 1\).
- Verifique que \(P(T^{A \rightarrow A} = \infty) > 0 \equiv P(T^{A \rightarrow A} < \infty) < 1\).
Definição 5.12 Se uma cadeia de Markov é irredutível e aperiódica, então ela possui uma distribuição limite estacionária \(\pi\), independente do estado inicial, tal que \(\pi P = \pi\).
Exemplo 5.27 Seja uma matriz estocástica \[P = \begin{bmatrix} 0.4 & 0.6 \\ 0.5 & 0.5 \end{bmatrix}\] Pela definição, \[\pi P = \pi \; \therefore \; \pi(P-I)=0\] Assim, \[\begin{bmatrix} \pi_1 & \pi_2 \end{bmatrix} \left(\begin{bmatrix} 0.4 & 0.6 \\ 0.5 & 0.5 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\right) = \begin{bmatrix} 0 & 0 \end{bmatrix}\] Escolhendo uma das equações, obtém-se \[-0.6\pi_1 + 0.5\pi_2 = 0\] Arbitrando um valor para uma das incógnitas, por exemplo \(\pi_1=1\), chega-se em \(\pi_2=1.2\). Logo, \(\pi=\begin{bmatrix} 1 & 1.2 \end{bmatrix}\). Normalizando se obtém \[\pi = \begin{bmatrix} \frac{1}{1+1.2} & \frac{1.2}{1+1.2} \end{bmatrix}=\begin{bmatrix} \frac{5}{11} & \frac{6}{11} \end{bmatrix}\] Conferindo, \[\begin{bmatrix} \frac{5}{11} & \frac{6}{11} \end{bmatrix} \begin{bmatrix} 0.4 & 0.6 \\ 0.5 & 0.5 \end{bmatrix} = \begin{bmatrix} \frac{5}{11} & \frac{6}{11} \end{bmatrix}\]
Biblioteca markovchain
A biblioteca markovchain (Spedicato 2017) oferece funções e métodos para criar e gerenciar cadeias de Markov de tempo discreto. A vinheta fornece alguns exemplos aplicados.
library(markovchain)
P <- matrix(c(.5,.2,.3, .15,.45,.4, .25,.35,.4),
nrow = 3, byrow = TRUE)
Pmc <- new('markovchain', transitionMatrix = P,
states = LETTERS[1:ncol(P)],
name='MarkovChain P')
Pmc## MarkovChain P
## A 3 - dimensional discrete Markov Chain defined by the following states:
## A, B, C
## The transition matrix (by rows) is defined as follows:
## A B C
## A 0.50 0.20 0.3
## B 0.15 0.45 0.4
## C 0.25 0.35 0.4## MarkovChain P Markov chain that is composed by:
## Closed classes:
## A B C
## Recurrent classes:
## {A,B,C}
## Transient classes:
## NONE
## The Markov chain is irreducible
## The absorbing states are: NONE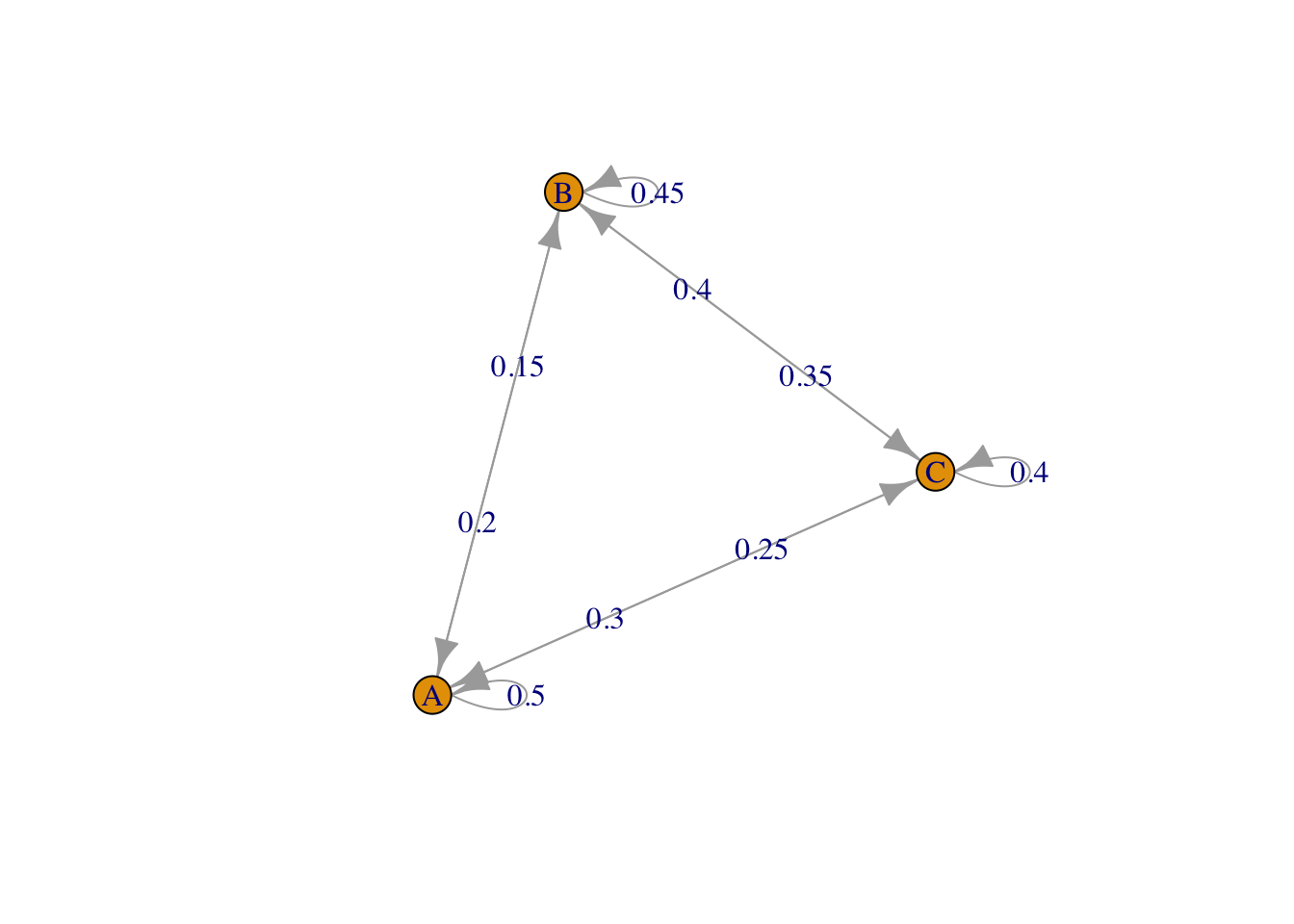
## A B C
## [1,] 0.2878788 0.3409091 0.3712121## [,1] [,2] [,3]
## [1,] 0.2878788 0.3409091 0.37121215.6.2.2 Metropolis-Hastings
The Metropolis algorithm (or Metropolis-Hastings algorithm) is a rejection algorithm that (…) requires only a function proportional to the distribution to be sampled, at the cost of requiring a rejection step from a particular candidate density. (Berry et al. 2011, 45)
Será considerado o algoritmo de Metropolis-Hastings descrito por (Robert and Casella 2010, 171). Está associado à densidade (alvo) \(f\) e à densidade condicional \(q\), produzindo uma cadeia de Markov \(X^{(t)}\) através do seguinte kernel de transição:
Dado \(x^{(t)}\),
1. Gere \(Y_t \sim q(y|x^{(t)})\).
2. Faça
\[X^{(t+1)} = \left\{
\begin{array}{lcl}
Y_t & \text{com probabilidade} & \rho(x^{(t)}, Y_t) \\
x^{(t)} & \text{com probabilidade} & 1-\rho(x^{(t)}, Y_t) \\ \end{array} \right. \]
onde
\[ \rho(x,y) = \min \left\{1, \frac{f(y)}{f(x)} \frac{q(x|y)}{q(y|x)}\right\} \]
A distribuição \(q\) é chamada de distribuição instrumental/proposta/candidata e \(\rho(x,y)\) é a probabilidade de aceitação de Metropolis-Hastings.
Exemplo 5.28 (Robert and Casella 2010, 172) simulam uma \(\mathcal{Beta}(2.7,6.3)\) a partir de uma \(\mathcal{U}(0,1)\).
a <- 2.7; b <- 6.3 # valores iniciais
Nsim <- 5000 # número de simulações
X <- runif(Nsim) # inicia a cadeia
Naccept <- 0
for (i in 2:Nsim){
Y <- runif(1)
rho <- min(1, (dbeta(Y,a,b)/dbeta(X[i-1],a,b)) * (1/1))
accept <- runif(1) < rho
X[i] <- X[i-1] + (Y - X[i-1])*accept
Naccept <- Naccept+accept
}
Naccept/Nsim # taxa de aceitação## [1] 0.452Validando.
bt <- rbeta(Nsim,a,b) # beta via stats::rbeta
ks.test(jitter(X), bt) # teste de aderência de Kolmogorov-Smirnov##
## Asymptotic two-sample Kolmogorov-Smirnov test
##
## data: jitter(X) and bt
## D = 0.0244, p-value = 0.1019
## alternative hypothesis: two-sidedplot(ecdf(X), col = 'blue', main = 'FDA empírica')
plot(ecdf(bt), col = 'red', add = TRUE)
legend(0, .9, legend=c('Metropolis-Hastings', 'stats::rbeta'),
lty = 1, col=c("red", "blue"), cex=0.8, bty = 'n')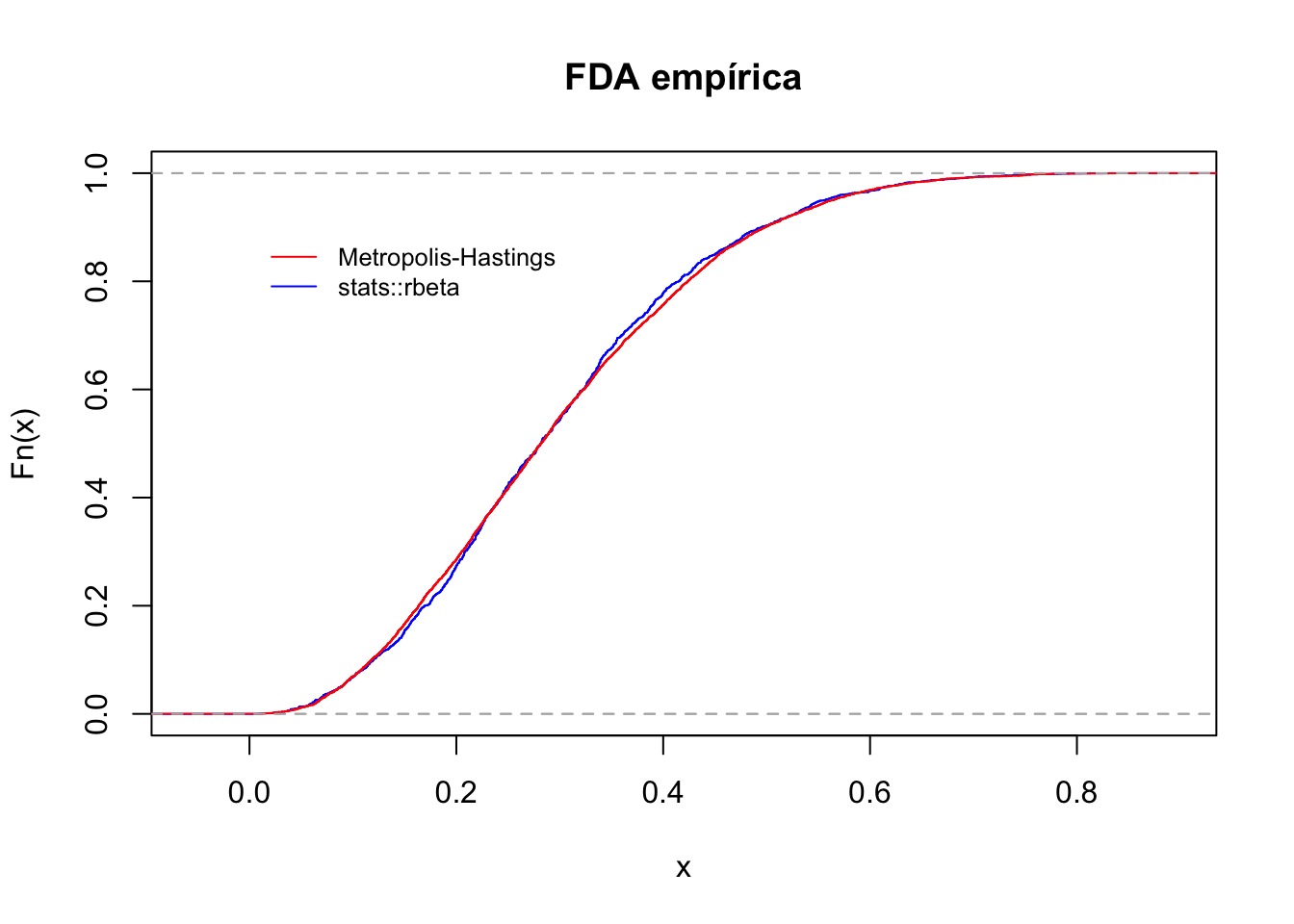
## [1] 0.3## [1] 0.2966724## [1] 0.021## [1] 0.02053429par(mfrow=c(1,2))
hist(X, freq = FALSE, main = 'Beta(2.7,6.3) via M-H')
curve(dbeta(x,a,b), col = 'blue', add = TRUE)
hist(bt, freq = FALSE, main = 'Beta(2.7,6.3) via stats::rbeta',
ylim=c(0,3))
curve(dbeta(x,a,b), col = 'red', add = TRUE)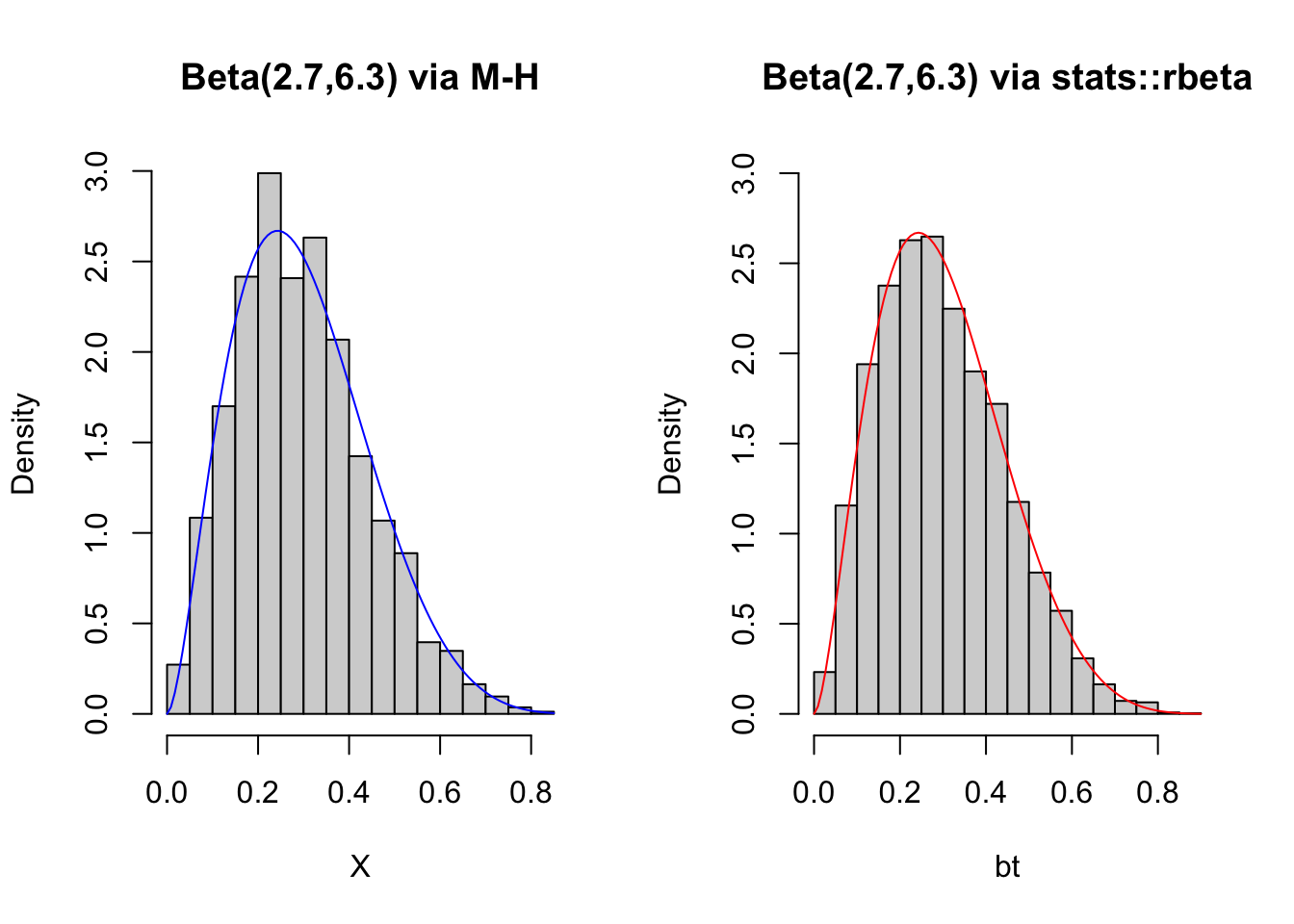
Exercício 5.20 Considerando o Exemplo 5.23.
- Faça a simulação de uma exponencial de parâmetro \(\lambda=1\) utilizando o algoritmo de Metropolis-Hastings.
- Compare os métodos da rejeição e de Metropolis-Hastings quanto ao tempo de processamento. O que você percebe?
5.6.3 Inferência variacional
The goal of variational inference is to approximate a conditional density of latent variables given observed variables. (Blei, Kucukelbir, and McAuliffe 2017, 4)
Exercício 5.21 Assista aos seguintes vídeos do canal de Chieh Wu. Total 1h39m48s.
- 23m54s Variational Inference Part 1 (Information theory).
- 28m00s Variational Inference Part 2 (Kullback–Leibler divergence).
- 10m05s Variational Inference Part 3 (Purpose of variational inference).
- 18m25s Variational Inference Part 4 (Derivation 1).
- 19m24s Variational Inference Part 5 (Derivation 2).
5.6.3.1 Informação
What we have done then is to take as our practical measure of information the logarithm of the number of possible symbol sequences. (R. V. Hartley 1928, 540)
Informação ou surpresa de uma distribuição de probabilidade \(\pi\) pode ser definida por \[\begin{equation} I(\pi) = \log \left( \frac{1}{\pi(x)} \right) = -\log \pi(x) \tag{5.8} \end{equation}\]
5.6.3.2 Entropia (de Shanon)
(Shannon 1948, 11) define entropia no caso discreto por \[\begin{equation} H(\pi) = - \sum_{x} \pi(x) \log_2 \pi(x) \tag{5.9} \end{equation}\]
\(H(\pi)\) pode ser interpretada como a informação média de uma V.A. discreta, ou ainda como o valor esperado da surpresa, já que \[\begin{equation} H(\pi) = \sum_{x} \left[ \log_2 \frac{1}{\pi(x)} \right] \pi(x) = E \left( \log_2 \frac{1}{\pi(x)} \right) \tag{5.10} \end{equation}\]
5.6.3.3 Entropia diferencial
Shannon assumed, without calculating, that the analog of \(\sum p_i \log p_i\) was \(\int w \log w dx\), and got into trouble for lack of invariance. (Jaynes 1963, 202)
A entropia diferencial é a informação média de uma V.A. contínua, e pode ser descrita simplificadamente por \[\begin{equation} H(\pi) = - \int_{x} \pi(x) \log \pi(x) dx \tag{5.11} \end{equation}\]
Para a medida invariante de entropia para o caso contínuo, veja a Eq. (63) de (Jaynes 1963).
5.6.3.4 Divergência de Kullback–Leibler
The idea behind VI is to first posit a family of densities and then to find the member of that family which is close to the target. Closeness is measured by Kullback-Leibler divergence. (Blei, Kucukelbir, and McAuliffe 2017, 1)
A divergência de Kullback-Leibler é uma medida de entropia relativa proposta por (Kullback and Leibler 1951). Quando baseada em \(P\), é definida por \[\begin{equation} D_{KL}(P||Q) = \sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)} \tag{5.12} \end{equation}\]
Quando baseada em \(Q\), define-se por \[\begin{equation} D_{KL}(Q||P) = \sum_{x \in X} Q(x) \log \frac{Q(x)}{P(x)} \tag{5.13} \end{equation}\]
Segundo (Kullback 1978, 6–7), \(D_{KL}(P||Q)\) e \(D_{KL}(Q||P)\) possuem todas as propriedades de uma distância (ou métrica), exceto pela desigualdade triangular, sendo portanto consideradas divergências direcionadas tais que \[D_{KL}(P||Q) \ne D_{KL}(Q||P)\]
Biblioteca philentropy
A biblioteca philentropy (Drost 2018) implementa medidas otimizadas de distância e similaridade para comparar funções de probabilidade. Para ilustrar o funcionamento da função philentropy::kullback_leibler_distance() utilizou-se o exemplo básico do artigo da Wikipedia.
P <- c(9/25,12/25,4/25)
Q <- c(1/3,1/3,1/3)
par(mfrow=c(1,2))
barplot(P, main = 'P, B(2,0.4)', names.arg = 0:2)
barplot(Q, main = 'Q, U{0,2}', names.arg = 0:2)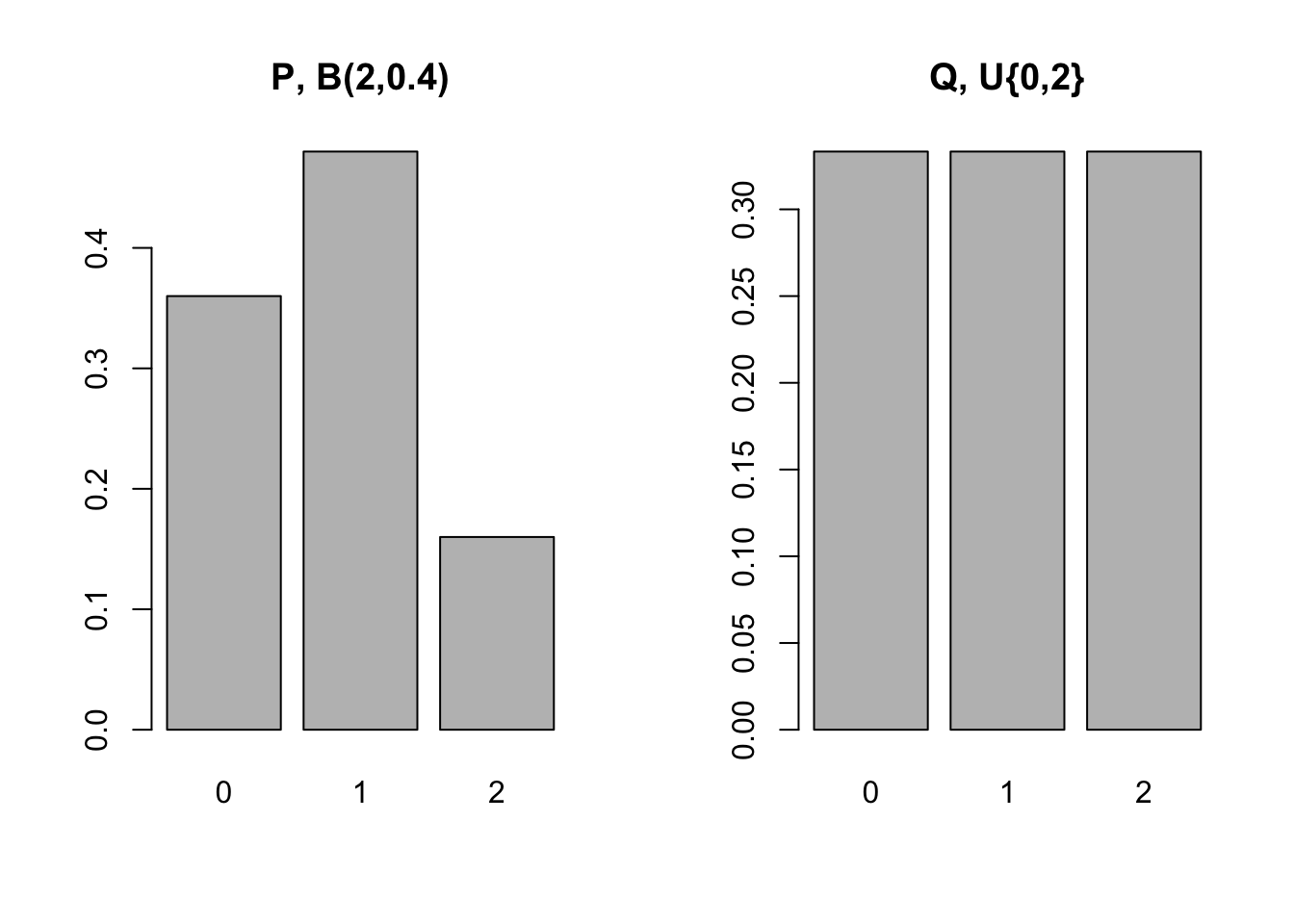
| \(x\) | 0 | 1 | 2 |
|---|---|---|---|
| \(P(x)\) | \(\frac{9}{25}\) | \(\frac{12}{25}\) | \(\frac{4}{25}\) |
| \(Q(x)\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) | \(\frac{1}{3}\) |
# libs
library(philentropy)
# D(P||Q)
kullback_leibler_distance(
P = c(9/25,12/25,4/25),
Q = c(1/3,1/3,1/3),
unit = 'log',
testNA = FALSE,
epsilon = 0.00001)## [1] 0.0852996# D(Q||P)
kullback_leibler_distance(
P = c(1/3,1/3,1/3),
Q = c(9/25,12/25,4/25),
unit = 'log',
testNA = FALSE,
epsilon = 0.00001)## [1] 0.097455015.6.3.5 ELBO (Evidence Lower BOund)
\[\text{Evidência} = \text{ELBO} + \text{KL}\]
Exercício 5.22
Exercício 5.23 Escreva o que você entendeu sobre:
- Teoria da Informação.
- Informação.
- Entropia.
- Entropia diferencial.
- Divergência de Kullback–Leibler.
- ELBO (Evidence Lower BOund).
- Inferência Variacional.
5.6.3.6 Para saber mais
Carlos Gomes faz um resumo dos tópicos discutidos pelo Journal Club - VAE, grupo destinado a discutir a arquitetura do Variational Auto-Encoder.
Anna-Lena Popkes faz algumas considerações sobre o tópico de Inferência Variacional.
5.6.4 Bootstrap
O método de bootstrap foi proposto por (Efron 1979). Dada uma amostra aleatória \(\boldsymbol{X}=(X_1, \ldots, X_n)\) de uma distribuição de probabilidades desconhecida \(F\), o método permite estimar a distribuição amostral de alguma variável aleatória \(R(\boldsymbol{X},F)\) com base nos dados observados \(\boldsymbol{x}\). Efron aplica o método em uma série de exemplos, tais como o cálculo da variância da mediana amostral, taxas de erro na análise discriminante linear e estimação de parâmetros de uma regressão.
De acordo com (Lehmann and Romano 2005, 671), ‘o teste via bootstrap pode ser visto com uma aproximação analítica do teste corrigido de Bartlett da razão de verossimilhança’. Assim, o bootstrap ‘captura automaticamente a correção de Bartlett’ com probabilidade de erro de rejeição igual a \(O(n^{-2})\), contra \(O(n^{-1})\) do teste de verossimilhança usual (Beran and Ducharme 1991).
(Efron and Hastie 2016) apresentam diversos exemplos, recomendando o ‘ambicioso’ pacote bootstrap (S et al. 2019). Há também o pacote boot (Canty and Ripley 2022) que implementa funções e conjuntos de dados de (Davison and Hinkley 1997).
Exemplo 5.29 Pode-se utilizar a função bootstrap::bootstrap() para estimar um intervalo de confiança para a média, comparado com o intervalo de confiança assintótico conforme Seção 6.2.2.
# gerando as re-amostras via bootstrap
library(bootstrap)
n <- 20
set.seed(4321); x <- rnorm(n, mean = 5, sd = 2)
theta <- function(x){mean(x)}
results <- bootstrap::bootstrap(x, 1000, theta)
# intervalo de confiança via bootstrap
m_boot <- mean(results$thetastar)
li_boot <- quantile(results$thetastar, .025)
ls_boot <- quantile(results$thetastar, .975)
c(li_boot, ls_boot)## 2.5% 97.5%
## 4.232709 5.778373# intervalo de confiança assintótico
li_ass <- mean(x)-1.96*sqrt(var(x)/n)
ls_ass <- mean(x)+1.96*sqrt(var(x)/n)
c(li_ass, ls_ass)## [1] 4.142245 5.833840# gráficos
hist(results$thetastar, 25, main = 'Estimativas via bootstrap')
abline(v = m_boot, col = 'red')
abline(v = li_boot, col = 'blue')
abline(v = ls_boot, col = 'blue')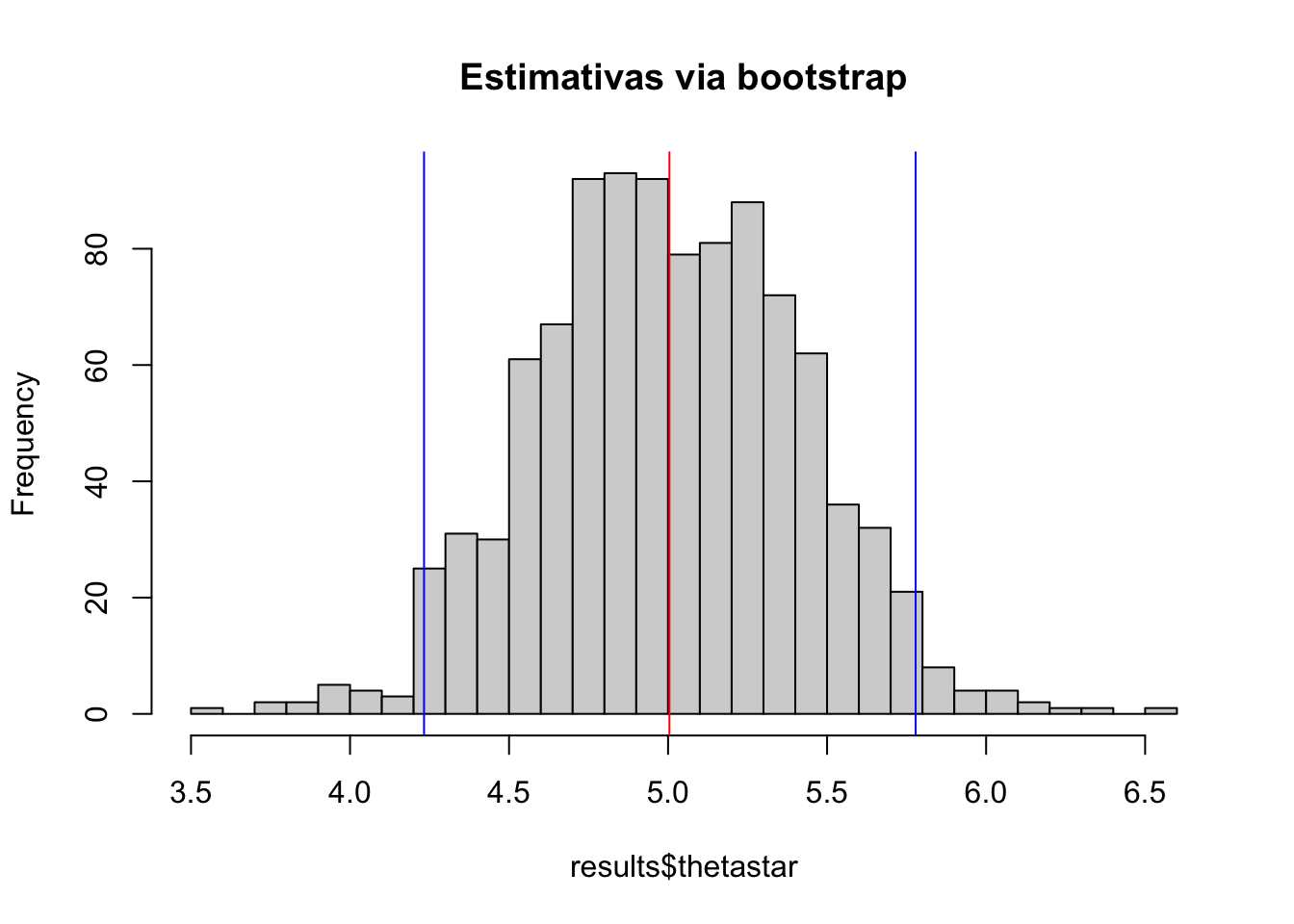
References
“Rejection sampling is a general method for simulating from an arbitrary posterior distribution, but it can be difficult to set up since it requires the construction of a suitable proposal density.” (Albert 2009, 117)↩︎
(Gelfand and Smith 1990) were the first authors to successfully point out to the statistical community at large that the sampling scheme devised by (Geman and Geman 1984) for Gibbs distributions could in fact be used for a host of other posterior distributions. (Gamerman and Lopes 2006, 141)↩︎