Capítulo 9
Solução. 9.8
# libs
library(car)
library(biotools)
library(MASS)
library(ggord)
# dados
data(wine, package='rattle')
head(wine)## Type Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids Proanthocyanins Color Hue
## 1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.04
## 2 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05
## 3 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03
## 4 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86
## 5 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04
## 6 1 14.20 1.76 2.45 15.2 112 3.27 3.39 0.34 1.97 6.75 1.05
## Dilution Proline
## 1 3.92 1065
## 2 3.40 1050
## 3 3.17 1185
## 4 3.45 1480
## 5 2.93 735
## 6 2.85 1450## 'data.frame': 178 obs. of 14 variables:
## $ Type : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
## $ Alcohol : num 14.2 13.2 13.2 14.4 13.2 ...
## $ Malic : num 1.71 1.78 2.36 1.95 2.59 1.76 1.87 2.15 1.64 1.35 ...
## $ Ash : num 2.43 2.14 2.67 2.5 2.87 2.45 2.45 2.61 2.17 2.27 ...
## $ Alcalinity : num 15.6 11.2 18.6 16.8 21 15.2 14.6 17.6 14 16 ...
## $ Magnesium : int 127 100 101 113 118 112 96 121 97 98 ...
## $ Phenols : num 2.8 2.65 2.8 3.85 2.8 3.27 2.5 2.6 2.8 2.98 ...
## $ Flavanoids : num 3.06 2.76 3.24 3.49 2.69 3.39 2.52 2.51 2.98 3.15 ...
## $ Nonflavanoids : num 0.28 0.26 0.3 0.24 0.39 0.34 0.3 0.31 0.29 0.22 ...
## $ Proanthocyanins: num 2.29 1.28 2.81 2.18 1.82 1.97 1.98 1.25 1.98 1.85 ...
## $ Color : num 5.64 4.38 5.68 7.8 4.32 6.75 5.25 5.05 5.2 7.22 ...
## $ Hue : num 1.04 1.05 1.03 0.86 1.04 1.05 1.02 1.06 1.08 1.01 ...
## $ Dilution : num 3.92 3.4 3.17 3.45 2.93 2.85 3.58 3.58 2.85 3.55 ...
## $ Proline : int 1065 1050 1185 1480 735 1450 1290 1295 1045 1045 ...##
## 1 2 3
## 59 71 48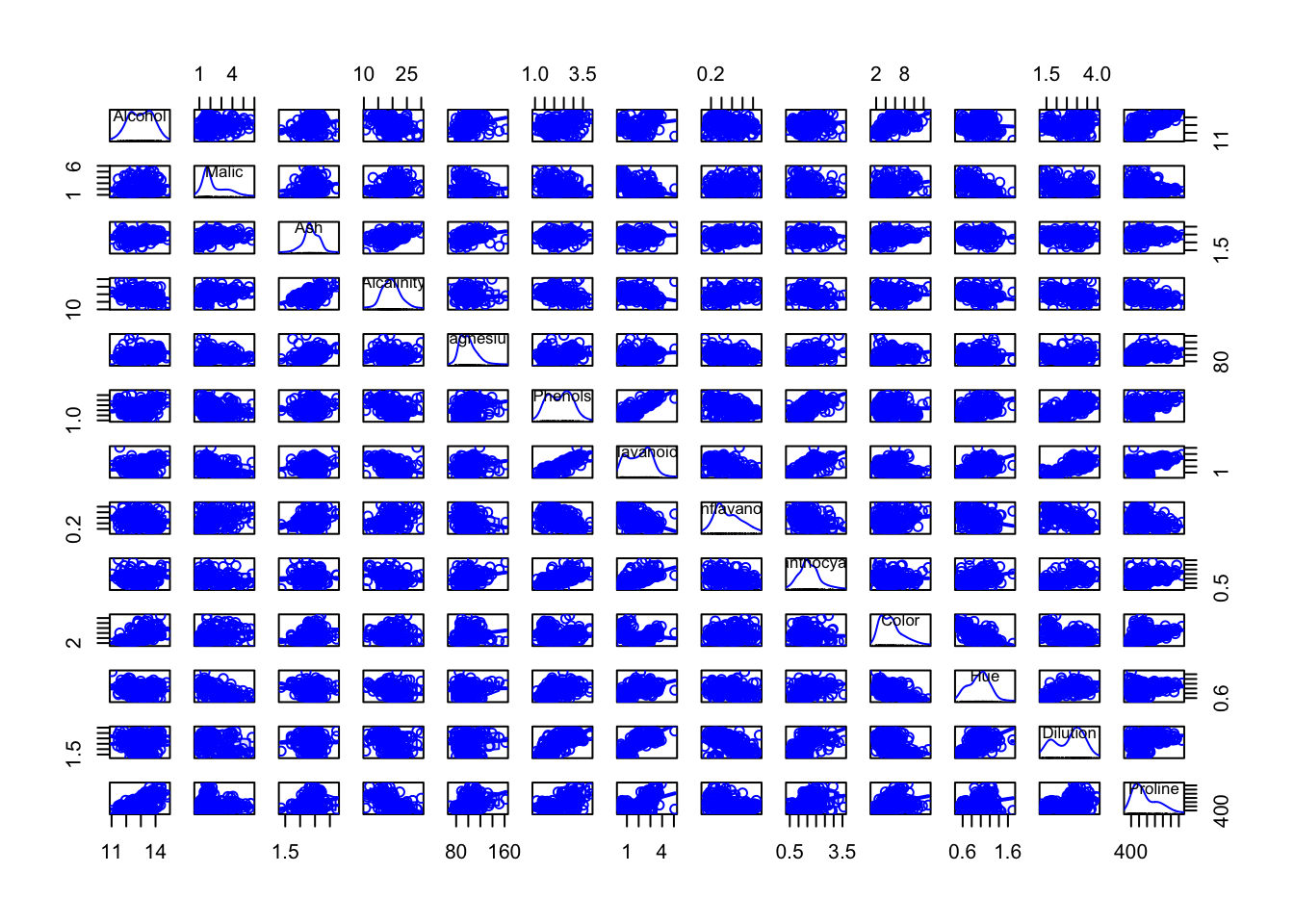
# testes de normalidade
for(i in 2:14){
print(colnames(wine)[i])
print(by(wine[,i], wine[,1], shapiro.test))
}## [1] "Alcohol"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98089, p-value = 0.4791
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97205, p-value = 0.114
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98147, p-value = 0.6408
##
## [1] "Malic"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.64698, p-value = 1.203e-10
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.83388, p-value = 1.84e-07
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98372, p-value = 0.7377
##
## [1] "Ash"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97016, p-value = 0.1556
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98604, p-value = 0.6198
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96085, p-value = 0.1092
##
## [1] "Alcalinity"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97315, p-value = 0.2161
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96878, p-value = 0.07397
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95976, p-value = 0.09874
##
## [1] "Magnesium"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96486, p-value = 0.08617
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.77903, p-value = 5.792e-09
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.94963, p-value = 0.03865
##
## [1] "Phenols"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95174, p-value = 0.0203
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98004, p-value = 0.318
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93967, p-value = 0.01577
##
## [1] "Flavanoids"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98419, p-value = 0.6387
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93719, p-value = 0.001498
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.89222, p-value = 0.0003561
##
## [1] "Nonflavanoids"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95539, p-value = 0.03015
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.9799, p-value = 0.3128
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.94383, p-value = 0.02284
##
## [1] "Proanthocyanins"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95579, p-value = 0.0315
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95157, p-value = 0.008146
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.8872, p-value = 0.0002491
##
## [1] "Color"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96819, p-value = 0.1251
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93175, p-value = 0.0008195
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95849, p-value = 0.08775
##
## [1] "Hue"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.96988, p-value = 0.1508
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97727, p-value = 0.2249
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.94616, p-value = 0.02819
##
## [1] "Dilution"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.9639, p-value = 0.07745
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97018, p-value = 0.08904
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.95791, p-value = 0.08311
##
## [1] "Proline"
## wine[, 1]: 1
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.98185, p-value = 0.5232
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 2
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.93868, p-value = 0.001774
##
## ---------------------------------------------------------------------------------
## wine[, 1]: 3
##
## Shapiro-Wilk normality test
##
## data: dd[x, ]
## W = 0.97694, p-value = 0.4585##
## Box's M-test for Homogeneity of Covariance Matrices
##
## data: wine[, -1]
## Chi-Sq (approx.) = 684.2, df = 182, p-value < 2.2e-16# amostra
set.seed(1); train <- sort(sample(1:nrow(wine), floor(nrow(wine)/2)))
table(wine$Type[train])##
## 1 2 3
## 26 37 26## Call:
## lda(Type ~ ., data = wine, prior = c(1, 1, 1)/3, subset = train)
##
## Prior probabilities of groups:
## 1 2 3
## 0.3333333 0.3333333 0.3333333
##
## Group means:
## Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids Proanthocyanins Color
## 1 13.66962 2.100385 2.425385 16.70385 104.80769 2.745769 2.9046154 0.2850000 1.876923 5.038846
## 2 12.24595 1.995676 2.234595 20.75676 93.00000 2.296216 2.1170270 0.3618919 1.703243 2.959459
## 3 13.12308 3.429615 2.425385 21.65385 99.15385 1.662308 0.7923077 0.4242308 1.145385 7.202692
## Hue Dilution Proline
## 1 1.0600000 3.241154 1024.6154
## 2 0.9954054 2.900000 515.3243
## 3 0.6861538 1.621923 624.6154
##
## Coefficients of linear discriminants:
## LD1 LD2
## Alcohol -0.502585734 0.922719326
## Malic -0.013458098 0.320879805
## Ash 0.660105781 1.736366924
## Alcalinity 0.156625731 -0.189504079
## Magnesium 0.011802512 0.007201424
## Phenols 0.720039984 0.238752126
## Flavanoids -1.865123430 -0.049217584
## Nonflavanoids -1.306490251 -0.806278387
## Proanthocyanins 0.257023116 -0.701998078
## Color 0.380036177 0.264765846
## Hue -1.028767178 -1.099953147
## Dilution -1.366936398 -0.473847413
## Proline -0.003195253 0.003713493
##
## Proportion of trace:
## LD1 LD2
## 0.7278 0.2722# predição
pred.lda <- predict(fit.lda, wine[-train,])
# gráficos
ggord(fit.lda, wine[-train,'Type'], ylim = c(-10, 10))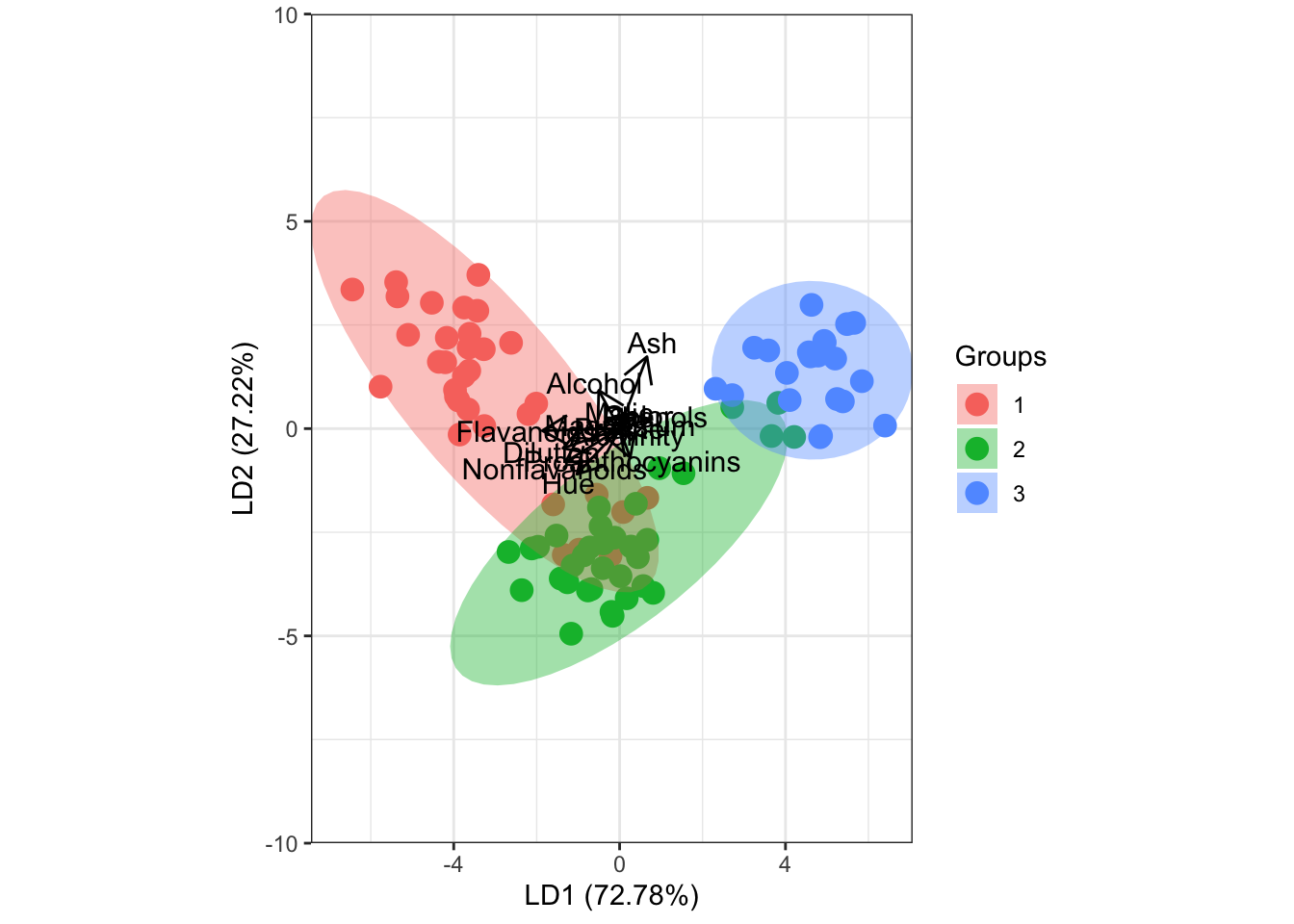
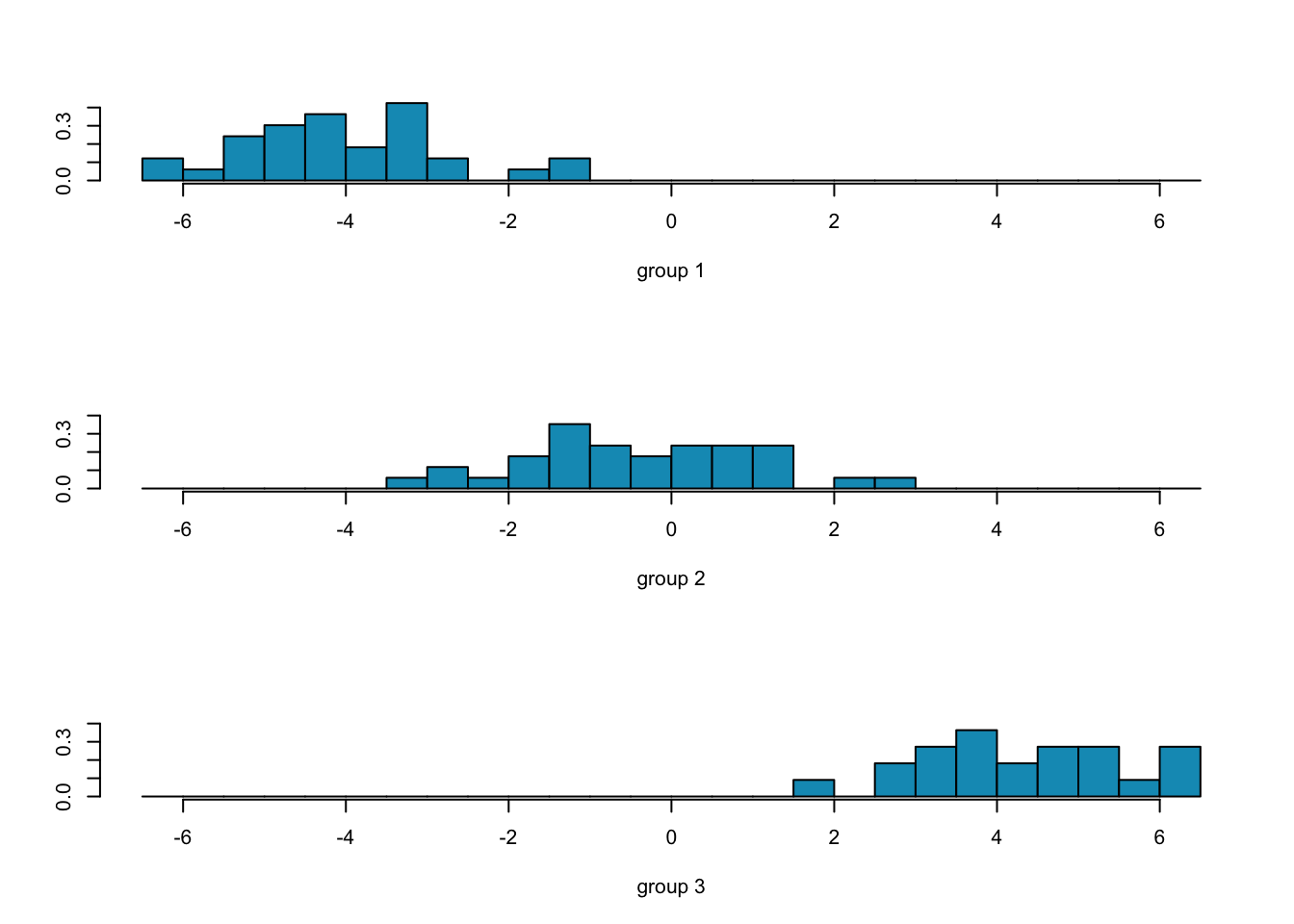
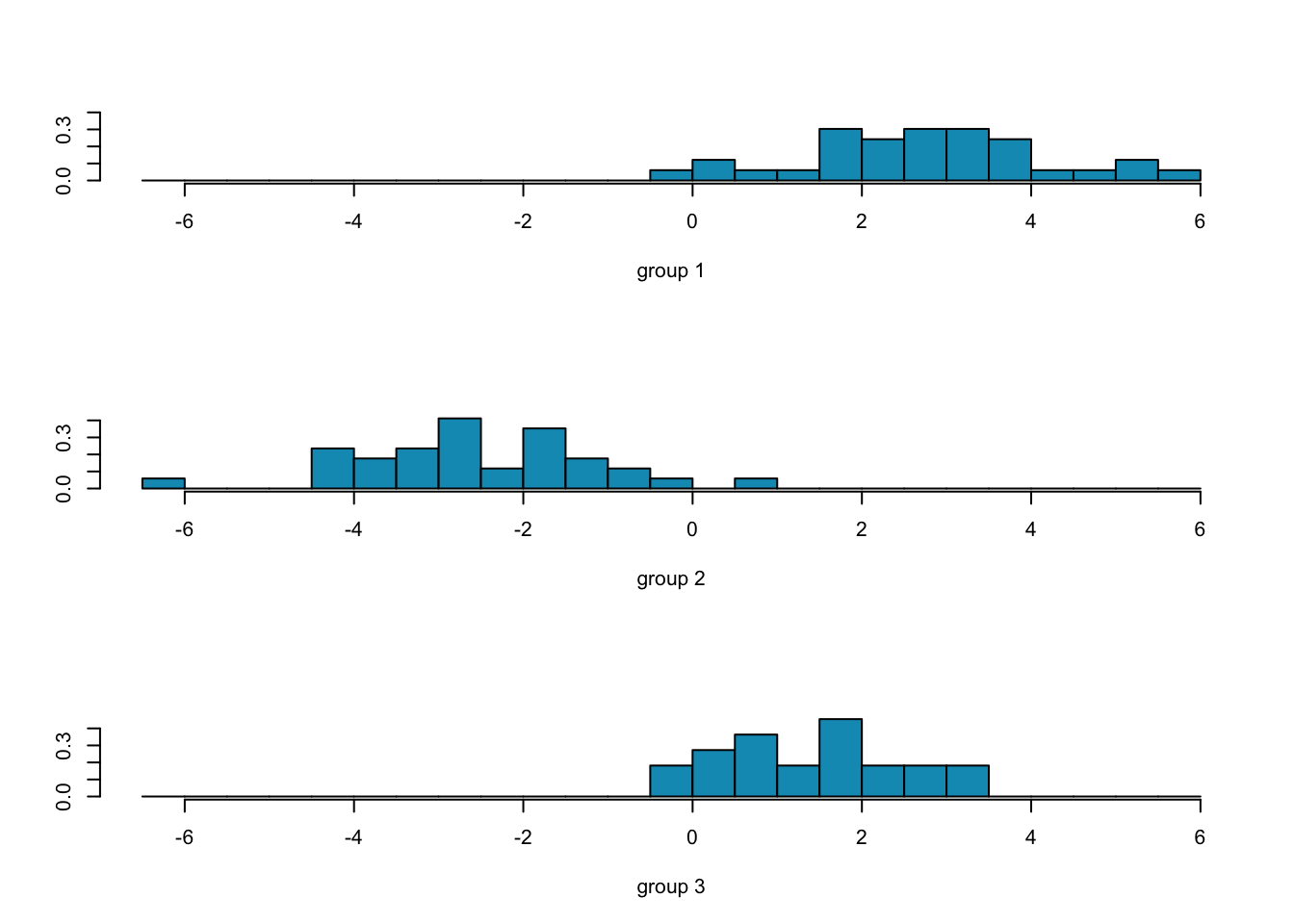
##
## 1 2 3
## 1 32 1 0
## 2 0 32 2
## 3 0 0 22## 1 2 3
## 0.9696970 0.9411765 1.0000000## [1] 0.9662921Solução. 9.18
# DAG com 3 nós e 3 arcos
dag3 <- bnlearn::empty.graph(LETTERS[1:3])
bnlearn::arcs(dag3) <- matrix(c('A', 'B',
'A', 'C',
'B', 'C'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
class(dag3)## [1] "bn"##
## Random/Generated Bayesian network
##
## model:
## [A][B|A][C|A:B]
## nodes: 3
## arcs: 3
## undirected arcs: 0
## directed arcs: 3
## average markov blanket size: 2.00
## average neighbourhood size: 2.00
## average branching factor: 1.00
##
## generation algorithm: Empty