9.18 Redes Bayesianas
Bayesian networks and their applications to real-world problems lie at the intersection of several fields such as probability and graph theory. (Nagarajan, Scutari, and Lèbre 2013, 1)
(Pearl 1988) fornece muitos dos fundamentos utilizados em Redes Bayesianas. (Huajie Zhang and Ling 2001) demonstram que qualquer rede Bayesiana pode ser representada por um clasificador bayesiano ingênuo aumentado (ANB na sigla em inglês). (Bang-Jensen and Gutin 2008) discutem em profundidade a teoria e aplicação de grafos direcionais (digraphs). (Korb and Nicholson 2011) abordam “redes bayesianas e aprendizado bayesiano de redes bayesianas (descoberta causal bayesiana) a partir de observação e experimento”. (Maathuis et al. 2018) trazem uma abordagem profunda e bastante atualizada de modelos gráficos.
A graphical model is a statistical model that is associated to a graph. The nodes of the graph correspond to the random variables of interest, and the edges encode allowed conditional dependencies among the variables. The factorization properties underlying graphical models facilitate tractable computation with multivariate distributions, making the models a valuable tool in a plethora of applications. (Maathuis et al. 2018 i)
9.18.1 Definições
Serão consideradas as definições de (Nagarajan, Scutari, and Lèbre 2013). Veja Understanding Bayesian Networks with Examples in R de Marco Scutari.
Redes bayesiana
Redes bayesianas são uma classe de modelos gráficos que permitem uma representação visual das dependências probabilísticas entre um determinado conjunto de variáveis aleatórias \(\boldsymbol{X} = \{ X_1, X_2, \ldots, X_p \}\) como um gráfico acíclico direcionado (DAG, na sigla em inglês) \(G = ( \boldsymbol{V}, A)\). Cada nó \(v_i \in \boldsymbol{V}\) corresponde a uma variável aleatória \(X_i\).
Grafos, nós e arcos
Um grafo é um conjunto não vazio \(\boldsymbol{N}\) de nós ou vértices e um conjunto finito \(A\) de pares de nós chamados arcos, elos ou arestas. Grafos podem ser não direcionais (undirected, \(G = (\boldsymbol{N}, E)\)), direcionais (directed/digraphs, \(G = (\boldsymbol{N}, A)\)) ou parcialmente direcionais (partially directed, \(G = (\boldsymbol{N}, A, E)\)). Os arcos não direcionais podem representar as duas orientações possíveis. Assim \(A-B\) é representado pelo par \(\{ A \rightarrow B, B \rightarrow A \}\). Na Figura 8.1 estão apresentados os três tipos de estrutura.
- O conjunto de nós do grafo não direcional é \(\boldsymbol{N}=\{A,B,C,D,E\}\) e o conjunto de elos (edges) é \(E=\{ (A-B), (A-C), (B-C), (C-D), (C-E), (D-E) \}\).
- O conjunto de nós do grafo direcional é \(\boldsymbol{N}=\{A,B,C,D,E\}\) e o conjunto de arcos é \(A=\{ (A \rightarrow B), (A \rightarrow C), (B \rightarrow C), (C \rightarrow D), (C \rightarrow E), (E \rightarrow D) \}\).
- O conjunto de nós do grafo direcional é \(\boldsymbol{N}=\{A,B,C,D,E\}\), caracterizado por um conjunto de elos \(E=\{ (C-E), (D-E) \}\) e um conjunto de arcos \(A=\{ (A \rightarrow B), (A \rightarrow C), (B \rightarrow C), (C \rightarrow D) \}\).

Exercício 9.16 Gere os grafos indicados na Figura 8.1.
Separações
Separação gráfica \(\perp\!\!\!\perp_G\): indica a ausência de um arco.
Independência probabilística \(\perp\!\!\!\perp_P\): indica que a observação de um nó não implica na alteração das probabilidades de outro nó.
D-separação: Se \(\boldsymbol{A}\), \(\boldsymbol{B}\) e \(\boldsymbol{C}\) são três subconjuntos disjuntos de nós em um grafo acíclico direcional G, então diz-se que \(\boldsymbol{C}\) \(d\)-separa \(\boldsymbol{A}\) de \(\boldsymbol{B}\), denotado \(\boldsymbol{A} \perp\!\!\!\perp_G \boldsymbol{B}|\boldsymbol{C}\), se ao longo de cada sequência de arcos entre um nó em \(\boldsymbol{A}\) e um nó em \(\boldsymbol{B}\) houver um nó \(\nu\) satisfazendo uma das seguintes condições:
1. \(\nu\) tem arcos convergentes (ou seja, há dois arcos apontando para \(\nu\) dos nós adjacentes no caminho) e nem \(\nu\) ou seus descendentes (ou seja, os nós que podem ser alcançados a partir de \(\nu\)) estão em \(\boldsymbol{C}\).
2. \(\nu\) está em \(\boldsymbol{C}\) e não possui arcos convergentes.
Manta de Markov (Markov blanket)
Em uma rede Bayesiana, a manta de Markov (Markov blanket) de um nó \(Z\) é o conjunto dos pais de \(Z\), os filhos de \(Z\) e todos os outros nós que compartilham um filho com \(Z\). Em termos mais técnicos, a manta de Markov representa o conjunto de nós que \(d\)-separa completamente um determinado nó do resto do grafo. Assim, a manta de Markov de um nó \(Z \in \boldsymbol{N}\) é o conjunto mínimo \(\boldsymbol{S}\) de \(\boldsymbol{N}\) tal que \[Z \perp\!\!\!\perp_P \boldsymbol{N}−\boldsymbol{S}−Z|\boldsymbol{S} \label{eq:markov-blanket}\]
9.18.2 Pacotes
(Nagarajan, Scutari, and Lèbre 2013) indicam vários pacotes no CRAN que lidam com redes Bayesianas. Podem ser divididos em duas categorias:
1. aqueles que tratam do aprendizado de estrutura
- bnlearn (Scutari 2010).
- deal (Bøttcher and Dethlefsen. 2022).
- pcalg (Markus Kalisch et al. 2012), (Alain Hauser and Peter Bühlmann 2012).
- catnet (Balov e Salzman, 2012).
2. aqueles que focam apenas no aprendizado de parâmetros e inferência
- gRbase (Dethlefsen and Højsgaard 2005).
- gRain (Højsgaard 2012).
Os pacotes do segundo grupo se concentram na manipulação dos parâmetros da rede, na previsão e na inferência, partindo do pressuposto de que todas as variáveis são discretas. Nem gRbase nem gRain implementam qualquer estrutura ou algoritmo de aprendizado de parâmetros, então a rede Bayesiana deve ser completamente especificada pelo usuário. Desta forma a parte computacional será abordada via bnlearn de (Scutari 2010).
9.18.2.1 bnlearn
As instruções para a instalação podem ser encontradas em bnlearn.com. No MacOS a biblioteca libgit2 deve estar disponível, e pode ser instalada via brew install libgit2. Além do pacote bnlearn, as dependências graph, Rgraphviz e RBGL devem ser instaladas via Bioconductor.
9.18.2.2 Elementos de bn
Os elementos de um grafo da classe bn são os seguintes:
learninguma lista contendo algumas informações sobre os resultados do algoritmo de aprendizagem da estrutura e seus parâmetros de ajuste, incluindo os testes de independência condicional e os escores da rede usados na análise. Não é alterado após a criação do objeto.
nodesuma lista contendo o total por nó. Cada elemento contém a manta de Markov, a vizinhança, os pais e os filhos desse nó específico.
arcsos arcos presentes na rede, no mesmo formato de duas colunas usado na chamada viaarcs(ug).
Exemplo 9.35 Elementos da rede bayesiana.
library(bnlearn)
# grafo direcional acíclico (DAG) com 4 nós e 3 arcos
dag <- empty.graph(LETTERS[1:4])
arcs(dag) <- matrix(c('A', 'B',
'B', 'A',
'A', 'C',
'A', 'D'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
class(dag)## [1] "bn"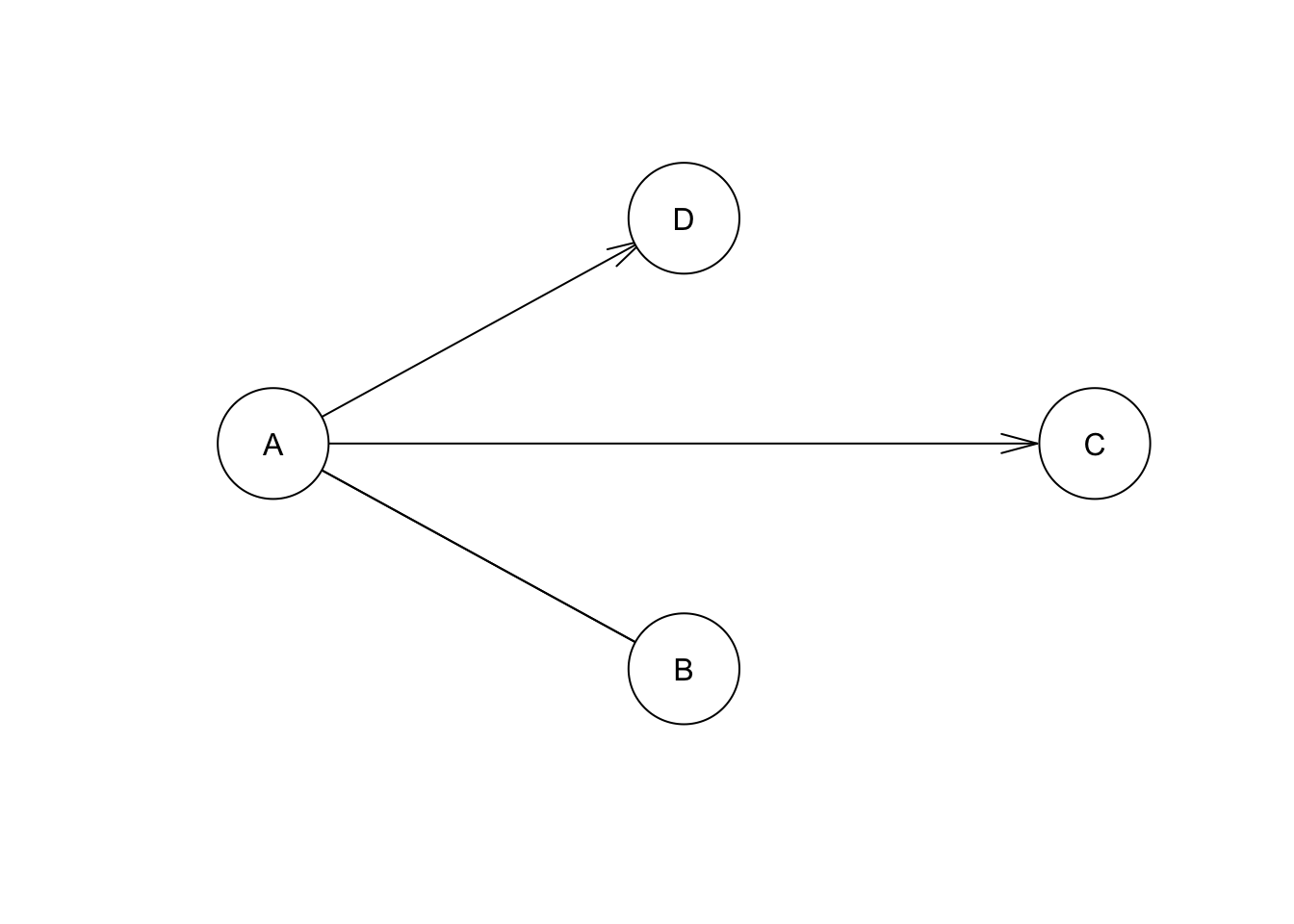
## $whitelist
## NULL
##
## $blacklist
## NULL
##
## $test
## [1] "none"
##
## $ntests
## [1] 0
##
## $algo
## [1] "empty"
##
## $args
## list()## $A
## $A$mb
## [1] "B" "C" "D"
##
## $A$nbr
## [1] "B" "C" "D"
##
## $A$parents
## character(0)
##
## $A$children
## [1] "C" "D"
##
##
## $B
## $B$mb
## [1] "A"
##
## $B$nbr
## [1] "A"
##
## $B$parents
## character(0)
##
## $B$children
## character(0)
##
##
## $C
## $C$mb
## [1] "A"
##
## $C$nbr
## [1] "A"
##
## $C$parents
## [1] "A"
##
## $C$children
## character(0)
##
##
## $D
## $D$mb
## [1] "A"
##
## $D$nbr
## [1] "A"
##
## $D$parents
## [1] "A"
##
## $D$children
## character(0)## from to
## [1,] "A" "B"
## [2,] "B" "A"
## [3,] "A" "C"
## [4,] "A" "D"9.18.2.3 Principais métricas
O resumo de um objeto da classe bn traz os seguintes elementos:
modelindica grafo não direcional ou as probabilidades condicionais em grafos direcionais.nodesindica o número de nós.
arcsindica o número de arcos não direcionais, direcionais e total.
average markov blanket size(\(ambs\)) indica o tamanho médio da manta de Markov.
average neighbourhood size(\(ans\)) indica o tamanho médio da vizinhança.
\[\begin{equation} ans = \frac{\#\text{vizinhos} \; A_1 + \ldots + \#\text{vizinhos} \; A_k}{\#\text{nós}} \tag{9.38} \end{equation}\] onde
average branching factor(\(abf\)) indica o número médio de arcos direcionais.
\[\begin{equation} abf = \frac{\#\text{arcos diretos}}{\#\text{nós}} \tag{9.39} \end{equation}\]
Exemplo 9.36 Métricas da rede bayesiana.
library(bnlearn)
# grafo não direcional com 2 nós e 1 arco
ug <- empty.graph(LETTERS[1:2])
arcs(ug) <- matrix(c('A', 'B',
'B', 'A'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
class(ug)## [1] "bn"##
## Random/Generated Bayesian network
##
## model:
## [undirected graph]
## nodes: 2
## arcs: 1
## undirected arcs: 1
## directed arcs: 0
## average markov blanket size: 1.00
## average neighbourhood size: 1.00
## average branching factor: 0.00
##
## generation algorithm: Empty# DAG com 2 nós e 1 arco
dag1 <- empty.graph(LETTERS[1:2])
arcs(dag1) <- matrix(c('A', 'B'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
class(dag1)## [1] "bn"##
## Random/Generated Bayesian network
##
## model:
## [A][B|A]
## nodes: 2
## arcs: 1
## undirected arcs: 0
## directed arcs: 1
## average markov blanket size: 1.00
## average neighbourhood size: 1.00
## average branching factor: 0.50
##
## generation algorithm: Empty# DAG com 3 nós e 2 arcos
dag2 <- empty.graph(LETTERS[1:3])
arcs(dag2) <- matrix(c('A', 'B',
'B', 'C'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
class(dag2)## [1] "bn"##
## Random/Generated Bayesian network
##
## model:
## [A][B|A][C|B]
## nodes: 3
## arcs: 2
## undirected arcs: 0
## directed arcs: 2
## average markov blanket size: 1.33
## average neighbourhood size: 1.33
## average branching factor: 0.67
##
## generation algorithm: Emptypar(mfrow = c(1,3))
plot(ug, main = 'a. Não direcional 2N1A')
plot(dag1, main = 'b. Direcional 2N1A')
plot(dag2, main = 'c. Direcional 3N2A')
Exercício 9.17 Considere o Exemplo @ref{exm:metrics).
a. Gere os grafos indicados pela Figura [8.3] tipos-grafos através de uma matriz de adjacência.
b. Explique os modelos apresentados.
c. Mostre o porque dos valores indicados de average markov blanket size.
d. Mostre o porque dos valores indicados de average neighbourhood size.
e. Mostre o porque dos valores indicados de average branching factor.
Exercício 9.18 Considere um DAG tal que \(\boldsymbol{N}=\{A,B,C\}\) e \(A=\{ (A \rightarrow B), (A \rightarrow C), (B \rightarrow C) \}\).
a. Estruture a rede.
b. Obtenha \(ambs\), \(ans\) e \(abf\).
9.18.2.4 Vizinhança e manta de Markov
library(bnlearn)
dag <- empty.graph(LETTERS[1:4])
arcs(dag) <- matrix(c('A', 'B',
'A', 'D',
'B', 'C',
'C', 'D'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
dag##
## Random/Generated Bayesian network
##
## model:
## [A][B|A][C|B][D|A:C]
## nodes: 4
## arcs: 4
## undirected arcs: 0
## directed arcs: 4
## average markov blanket size: 2.50
## average neighbourhood size: 2.00
## average branching factor: 1.00
##
## generation algorithm: Empty
## [1] "B" "D"## [1] "A" "C"## [1] "B" "D"## [1] "A" "C"## [1] "B" "C" "D"## [1] "A" "C"## [1] "A" "B" "D"## [1] "A" "C"Exemplo 9.37 Considere o banco de dados investigado originalmente por (Kent, Bibby, and Mardia 1979), com desdobramentos propostos por (Whittaker 1990) e apresentado em detalhes por (Nagarajan, Scutari, and Lèbre 2013, 26). São apresentadas notas em provas – delimitadas no intervalo [0,100] – realizadas por 88 alunos em cinco disciplinas: mecânica (MECH), vetores (VECT), álgebra (ALG), análise (ANL) e estatística (STAT).
## 'data.frame': 88 obs. of 5 variables:
## $ MECH: num 77 63 75 55 63 53 51 59 62 64 ...
## $ VECT: num 82 78 73 72 63 61 67 70 60 72 ...
## $ ALG : num 67 80 71 63 65 72 65 68 58 60 ...
## $ ANL : num 67 70 66 70 70 64 65 62 62 62 ...
## $ STAT: num 81 81 81 68 63 73 68 56 70 45 ...Pode-se criar um grafo vazio com os nós correspondentes às variáveis de marks usando a função empty.graph. Note que para a criação de um gráfico não direcional é necessário conectar todos os nós dois a dois. A estrutura utilizada é de (Whittaker 1990).
ug <- empty.graph(names(marks))
arcs(ug) <- matrix( c('MECH', 'VECT',
'VECT', 'MECH',
'MECH', 'ALG',
'ALG', 'MECH',
'VECT', 'ALG',
'ALG', 'VECT',
'ALG', 'ANL',
'ANL', 'ALG',
'ALG', 'STAT',
'STAT', 'ALG',
'ANL', 'STAT',
'STAT', 'ANL'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
ug##
## Random/Generated Bayesian network
##
## model:
## [undirected graph]
## nodes: 5
## arcs: 6
## undirected arcs: 6
## directed arcs: 0
## average markov blanket size: 2.40
## average neighbourhood size: 2.40
## average branching factor: 0.00
##
## generation algorithm: Emptydag <- empty.graph(names(marks))
arcs(dag) <- matrix( c('VECT', 'MECH',
'ALG', 'MECH',
'ALG', 'VECT',
'ANL', 'ALG',
'STAT', 'ALG',
'STAT', 'ANL'),
ncol = 2, byrow = TRUE,
dimnames = list(c(), c('from', 'to')))
dag##
## Random/Generated Bayesian network
##
## model:
## [STAT][ANL|STAT][ALG|ANL:STAT][VECT|ALG][MECH|VECT:ALG]
## nodes: 5
## arcs: 6
## undirected arcs: 0
## directed arcs: 6
## average markov blanket size: 2.40
## average neighbourhood size: 2.40
## average branching factor: 1.20
##
## generation algorithm: EmptyPode-se explorar, é claro, as estruturas de forma gráfica.

Outra forma de entrada de dados é a partir de uma matriz de adjacência.
mat <- matrix(c(0,1,1,0,0, # MECH
0,0,1,0,0, # VECT
0,0,0,1,1, # ALG
0,0,0,0,1, # ANL
0,0,0,0,0), # STAT
nrow = 5,
dimnames = list(nodes(dag), nodes(dag)))
mat## MECH VECT ALG ANL STAT
## MECH 0 0 0 0 0
## VECT 1 0 0 0 0
## ALG 1 1 0 0 0
## ANL 0 0 1 0 0
## STAT 0 0 1 1 0## [1] TRUEPode-se estar interessado em criar um novo objeto da classe bn modificando um existente. A maneira mais direta de fazer isso é adicionando (set.arc), eliminando (drop.arc) ou revertendo (rev.arc) arcos na rede original.
dag3 <- empty.graph(nodes(dag))
dag3 <- set.arc(dag3, 'VECT', 'MECH')
dag3 <- set.arc(dag3, 'ALG', 'MECH')
dag3 <- set.arc(dag3, 'ALG', 'VECT')
dag3 <- set.arc(dag3, 'ANL', 'ALG')
dag3 <- set.arc(dag3, 'STAT', 'ALG')
dag3 <- set.arc(dag3, 'STAT', 'ANL')
all.equal(dag, dag3)## [1] TRUEPode-se investigar a estrutura da rede.
## [1] "STAT" "ANL" "ALG" "VECT" "MECH"## [1] "ALG" "ANL"## [1] "ALG" "ANL"## [1] "ALG" "ANL"Vários critérios de pontuação foram propostos no contexto de aprendizagem de estrutura. O exemplo abaixo demonstra a pontuação de log-verossimilhança de uma rede Bayesiana e como ela muda em resposta às mudanças na estrutura do gráfico. Mais importante, ele demonstra a invariância do log-verossimilhança para redes na mesma classe de equivalência que o esperado.
## [1] -1695.589É possível aprender a estrutura da rede (classes de equivalência) de grafos acíclicos direcionais através de algoritmos disponíveis no pacote bnlearn. Veja ?gs.
##
## Bayesian network learned via Constraint-based methods
##
## model:
## [undirected graph]
## nodes: 5
## arcs: 6
## undirected arcs: 6
## directed arcs: 0
## average markov blanket size: 2.40
## average neighbourhood size: 2.40
## average branching factor: 0.00
##
## learning algorithm: Grow-Shrink
## conditional independence test: Pearson's Correlation
## alpha threshold: 0.05
## tests used in the learning procedure: 80Exemplo 9.38 Exemplo disponível em https://www.r-bloggers.com/2015/02/bayesian-network-in-r-introduction/.
Dados:
- Smoking (smoking): a two-level factor with levels no and yes.
- M. Work (strenuous mental work): a two-level factor with levels no and yes.
- P. Work (strenuous physical work): a two-level factor with levels no and yes.
- Pressure (systolic blood pressure): a two-level factor with levels <140 and >140.
- Proteins (ratio of beta and alpha lipoproteins): a two-level factor with levels.
- Family (family anamnesis of coronary heart disease): a two-level factor with levels neg and pos.
## Smoking M. Work P. Work Pressure Proteins Family
## 1 no no no <140 <3 neg
## 2 no no no <140 <3 neg
## 3 no no no <140 <3 neg
## 4 no no no <140 <3 neg
## 5 no no no <140 <3 neg
## 6 no no no <140 <3 negAprendendo a estrutura com o algoritmo hill-climbing (HC).
##
## Bayesian network learned via Score-based methods
##
## model:
## [Smoking][P..Work|Smoking][Pressure|Smoking][M..Work|Smoking:P..Work:Pressure][Proteins|Smoking:M..Work]
## [Family|M..Work]
## nodes: 6
## arcs: 8
## undirected arcs: 0
## directed arcs: 8
## average markov blanket size: 3.00
## average neighbourhood size: 2.67
## average branching factor: 1.33
##
## learning algorithm: Hill-Climbing
## score: BIC (disc.)
## penalization coefficient: 3.759032
## tests used in the learning procedure: 65
## optimized: TRUE
Retirando associação entre família e trabalho mental estressante.
Treinando.
##
## Bayesian network parameters
##
## Parameters of node Smoking (multinomial distribution)
##
## Conditional probability table:
## no yes
## 0.5219989 0.4780011
##
## Parameters of node M..Work (multinomial distribution)
##
## Conditional probability table:
##
## , , P..Work = no, Pressure = <140
##
## Smoking
## M..Work no yes
## no 0.2668919 0.6260504
## yes 0.7331081 0.3739496
##
## , , P..Work = yes, Pressure = <140
##
## Smoking
## M..Work no yes
## no 0.8995434 0.8571429
## yes 0.1004566 0.1428571
##
## , , P..Work = no, Pressure = >140
##
## Smoking
## M..Work no yes
## no 0.2745902 0.2684564
## yes 0.7254098 0.7315436
##
## , , P..Work = yes, Pressure = >140
##
## Smoking
## M..Work no yes
## no 0.8861386 0.8385417
## yes 0.1138614 0.1614583
##
##
## Parameters of node P..Work (multinomial distribution)
##
## Conditional probability table:
##
## Smoking
## P..Work no yes
## no 0.5619147 0.4397727
## yes 0.4380853 0.5602273
##
## Parameters of node Pressure (multinomial distribution)
##
## Conditional probability table:
##
## Smoking
## Pressure no yes
## <140 0.5359001 0.6125000
## >140 0.4640999 0.3875000
##
## Parameters of node Proteins (multinomial distribution)
##
## Conditional probability table:
##
## , , M..Work = no
##
## Smoking
## Proteins no yes
## <3 0.6685824 0.6167763
## >3 0.3314176 0.3832237
##
## , , M..Work = yes
##
## Smoking
## Proteins no yes
## <3 0.5671982 0.3235294
## >3 0.4328018 0.6764706
##
##
## Parameters of node Family (multinomial distribution)
##
## Conditional probability table:
##
## M..Work
## Family no yes
## neg 0.8814159 0.8227848
## pos 0.1185841 0.1772152Inferindo.
## [1] 0.4259579