9.1 Análise de Componentes Principais

A Análise de Componentes Principais (PCA na sigla em inglês) é uma técnica de redução de dimensionalidade usualmente aplicada a um grande número de variáveis relacionadas, de forma a capturar o máximo possível da variabilidade do conjunto de dados. Foi introduzida por (Pearson 1901) e estudada independentemente por (Hotelling 1933) e outros pesquisadores que abordaram o problema de formas variadas. Considerando a definição de (Bishop 1999), seja um conjunto de dados \(X\) de dimensão \(n \times p\) composto por \(n\) vetores \(p\)-dimensionais conforme indicado a seguir. \[ X = \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,p} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n,1} & x_{n,2} & \cdots & x_{n,p} \end{bmatrix} = \begin{bmatrix} \boldsymbol{x}_{1} \\ \boldsymbol{x}_{2} \\ \vdots \\ \boldsymbol{x}_{n} \end{bmatrix} \]

9.1.1 Via matriz de covariâncias \(S\)

Deste conjunto de dados calcula-se a matriz de covariâncias amostrais \(S\) conforme Eq. (4.17). São obtidos os autovalores \(\lambda\) associados aos autovetores \(\boldsymbol{v}_i \ne \boldsymbol{0}\) da matriz \(S\) pela equação (3.15), \(i=1,\ldots,p\). Os autovetores correspondentes aos \(q\) maiores autovetores (\(q<p\)) são mantidos, e uma representação de dimensão reduzida é definida por uma combinação linear dos autovetores e dos dados deslocados pela média.

Exemplo 9.1 Pode-se calcular os autovetores e autovalores das colunas numéricas do banco de dados iris.

df <- iris              # simplificando/padronizando o nome da base de dados
(m <- colMeans(df[-5])) # vetor de medias

## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##     5.843333     3.057333     3.758000     1.199333

(S <- cov(df[-5]))      # matriz de covariancias

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    0.6856935  -0.0424340    1.2743154   0.5162707
## Sepal.Width    -0.0424340   0.1899794   -0.3296564  -0.1216394
## Petal.Length    1.2743154  -0.3296564    3.1162779   1.2956094
## Petal.Width     0.5162707  -0.1216394    1.2956094   0.5810063

eigen(S)                # autovalores (variancias) e autovetores de S

## eigen() decomposition
## $values
## [1] 4.22824171 0.24267075 0.07820950 0.02383509
## 
## $vectors
##             [,1]        [,2]        [,3]       [,4]
## [1,]  0.36138659  0.65658877  0.58202985  0.3154872
## [2,] -0.08452251  0.73016143 -0.59791083 -0.3197231
## [3,]  0.85667061 -0.17337266 -0.07623608 -0.4798390
## [4,]  0.35828920 -0.07548102 -0.54583143  0.7536574

(av <- prcomp(df[-5]))  # via funcao

## Standard deviations (1, .., p=4):
## [1] 2.0562689 0.4926162 0.2796596 0.1543862
## 
## Rotation (n x k) = (4 x 4):
##                      PC1         PC2         PC3        PC4
## Sepal.Length  0.36138659 -0.65658877  0.58202985  0.3154872
## Sepal.Width  -0.08452251 -0.73016143 -0.59791083 -0.3197231
## Petal.Length  0.85667061  0.17337266 -0.07623608 -0.4798390
## Petal.Width   0.35828920  0.07548102 -0.54583143  0.7536574

Pode-se investigar o objeto av.

names(av)

## [1] "sdev"     "rotation" "center"   "scale"    "x"

class(av)

## [1] "prcomp"

av$rotation

##                      PC1         PC2         PC3        PC4
## Sepal.Length  0.36138659 -0.65658877  0.58202985  0.3154872
## Sepal.Width  -0.08452251 -0.73016143 -0.59791083 -0.3197231
## Petal.Length  0.85667061  0.17337266 -0.07623608 -0.4798390
## Petal.Width   0.35828920  0.07548102 -0.54583143  0.7536574

Mais alguns exercícios.

# Calculando a primeira componente principal 'na mão'
pc1 <- av$rotation[1,1]*df[,1] +
  av$rotation[2,1]*df[,2] +
  av$rotation[3,1]*df[,3] +
  av$rotation[4,1]*df[,4]

# colando e removendo pc1
df <- cbind(iris, pc1)
rm(pc1)

# dando uma olhada
head(df)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species      pc1
## 1          5.1         3.5          1.4         0.2  setosa 2.818240
## 2          4.9         3.0          1.4         0.2  setosa 2.788223
## 3          4.7         3.2          1.3         0.2  setosa 2.613375
## 4          4.6         3.1          1.5         0.2  setosa 2.757022
## 5          5.0         3.6          1.4         0.2  setosa 2.773649
## 6          5.4         3.9          1.7         0.4  setosa 3.221505

plot(df$Species, df$pc1)

all.equal(var(df$pc1), eigen(S)$values[1])

## [1] TRUE

all.equal(sd(df$pc1), av$sdev[1])

## [1] TRUE

# Simulação
library(e1071)
M <- 10^3
n <- nrow(df)
prop_train <- .7
acc <- matrix(nrow = M, ncol = 2)
colnames(acc) <- c('acc_null', 'acc_pc1')
  
ini <- Sys.time()
for(i in 1:M){
  # amostras de treino e teste
  set.seed(i); itrain <- sort(sample(1:n, floor(prop_train*n)))
  itest <- setdiff(1:n, itrain)
  
  # classificador SVM com todas as variaveis
  fit0 <- e1071::svm(Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, 
                     data = df[itrain,])
  
  # cl. SVM somente com pc1
  fit1 <- svm(Species ~ pc1, 
              data = df[itrain,])
  
  # predicao
  pre0 <- predict(fit0, df[itest,])
  tab <- table(pre0, df[itest, 'Species'])
  acc[i,1] <- sum(diag(tab)/sum(tab))
  
  pre1 <- predict(fit1, df[itest,])
  tab <- table(pre1, df[itest, 'Species'])
  acc[i,2] <- sum(diag(tab)/sum(tab))
  
  # if(i%%.1*M == 0){
  #   print(paste0(i/M*100, ' %'))
  # }
}
Sys.time()-ini

## Time difference of 3.024172 secs

head(acc)

##       acc_null   acc_pc1
## [1,] 0.9777778 0.9111111
## [2,] 0.9111111 0.8444444
## [3,] 0.9777778 0.9555556
## [4,] 0.9777778 0.9555556
## [5,] 0.9555556 0.9111111
## [6,] 0.9777778 1.0000000

apply(acc, 2, summary)

##          acc_null   acc_pc1
## Min.    0.8666667 0.8222222
## 1st Qu. 0.9333333 0.9111111
## Median  0.9555556 0.9333333
## Mean    0.9584222 0.9243333
## 3rd Qu. 0.9777778 0.9555556
## Max.    1.0000000 1.0000000

9.1.2 Via matriz de correlação \(R\)

É possível realizar o mesmo procedimento na matriz de correlação \(R\) dada pela Eq. (4.24). Esta abordagem é recomendada para evitar que os resultados sejam afetados pela escala dos valores observados.

(R <- cor(df[-5]))  # matriz de correlação

##              Sepal.Length Sepal.Width Petal.Length Petal.Width        pc1
## Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411  0.8974018
## Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259 -0.3987485
## Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654  0.9978739
## Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000  0.9665475
## pc1             0.8974018  -0.3987485    0.9978739   0.9665475  1.0000000

eigen(R)            # autovalores e autovetores de R

## eigen() decomposition
## $values
## [1] 3.911658e+00 9.166484e-01 1.474599e-01 2.423405e-02 5.028510e-16
## 
## $vectors
##            [,1]         [,2]        [,3]       [,4]        [,5]
## [1,]  0.4522259 -0.356806670  0.73993342 -0.3275283 -0.11577781
## [2,] -0.2227481 -0.932011105 -0.24995244  0.1380551  0.01425325
## [3,]  0.5026424 -0.003345711 -0.12406502  0.6241962 -0.58508668
## [4,]  0.4887010 -0.045988343 -0.60912426 -0.6138891 -0.10566043
## [5,]  0.5043778 -0.043797032 -0.05998183  0.3273916  0.79555125

prcomp(df[-5], scale = T)  # via função, scale = TRUE

## Standard deviations (1, .., p=5):
## [1] 1.977791e+00 9.574176e-01 3.840051e-01 1.556729e-01 7.632427e-16
## 
## Rotation (n x k) = (5 x 5):
##                     PC1          PC2         PC3        PC4         PC5
## Sepal.Length  0.4522259 -0.356806670  0.73993342 -0.3275283 -0.11577781
## Sepal.Width  -0.2227481 -0.932011105 -0.24995244  0.1380551  0.01425325
## Petal.Length  0.5026424 -0.003345711 -0.12406502  0.6241962 -0.58508668
## Petal.Width   0.4887010 -0.045988343 -0.60912426 -0.6138891 -0.10566043
## pc1           0.5043778 -0.043797032 -0.05998183  0.3273916  0.79555125

9.1.3 Proporção da variância explicada

A proporção da variância explicada pelo \(i\)-ésimo componente principal é dada pela Eq. (9.1), e pode ser visualizada em um gráfico ordenado, o screeplot proposto por (Cattell 1966) para testar o número de fatores. \[\begin{equation} PVE_i = \dfrac{\lambda_i}{\sum_{j=1}^{p} \lambda_j} \tag{9.1} \end{equation}\]

(vS <- eigen(S)$values) # autovalores (variâncias) a partir de S

## [1] 4.22824171 0.24267075 0.07820950 0.02383509

vS/sum(vS)  # Equação (17)

## [1] 0.924618723 0.053066483 0.017102610 0.005212184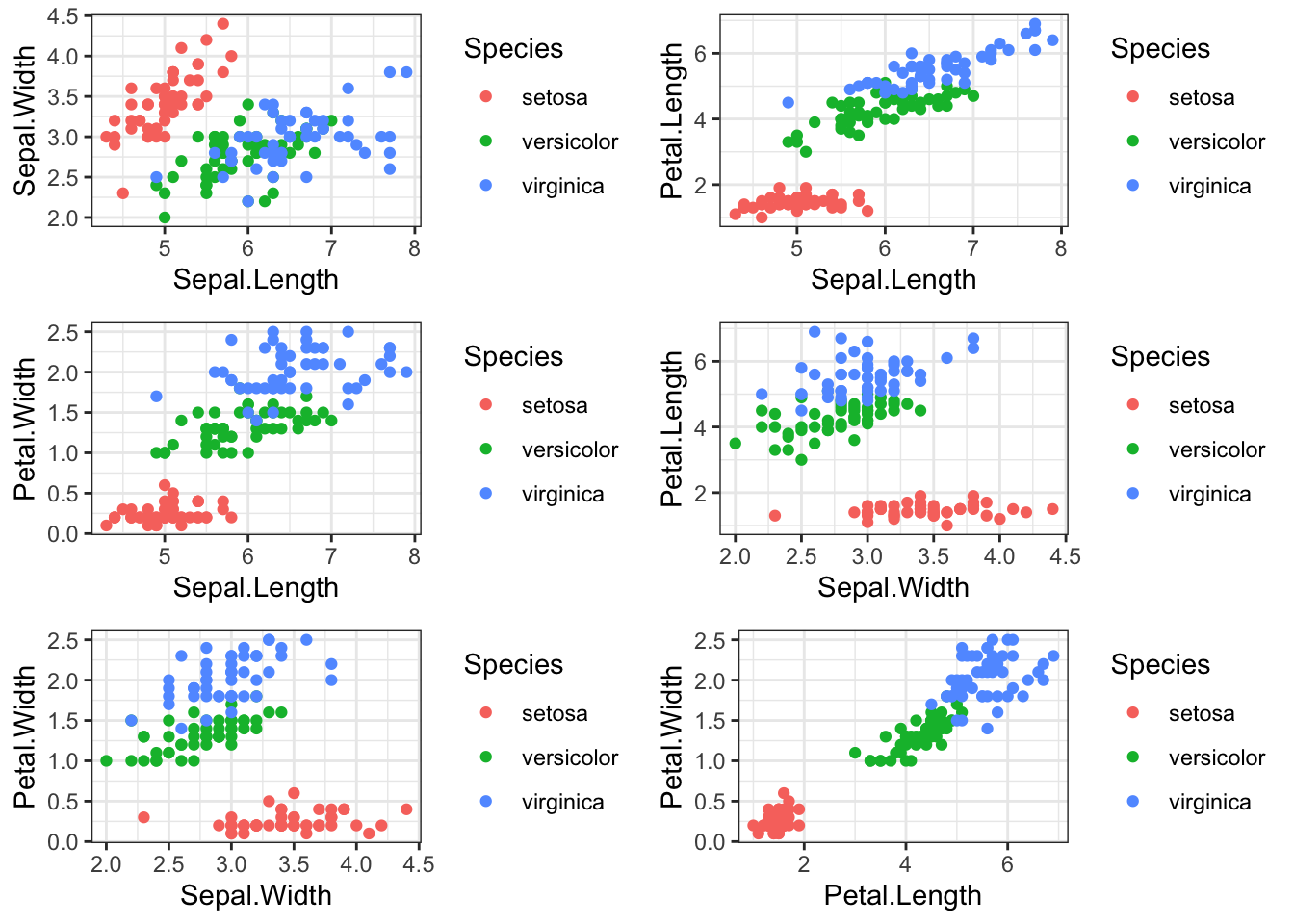

screeplot(prcomp(df[-5]), type = 'lines')

(vR <- eigen(R)$values) # autovalores (variâncias) a partir de R

## [1] 3.911658e+00 9.166484e-01 1.474599e-01 2.423405e-02 5.028510e-16

vR/sum(vR)  # Equação (17)

## [1] 7.823315e-01 1.833297e-01 2.949199e-02 4.846810e-03 1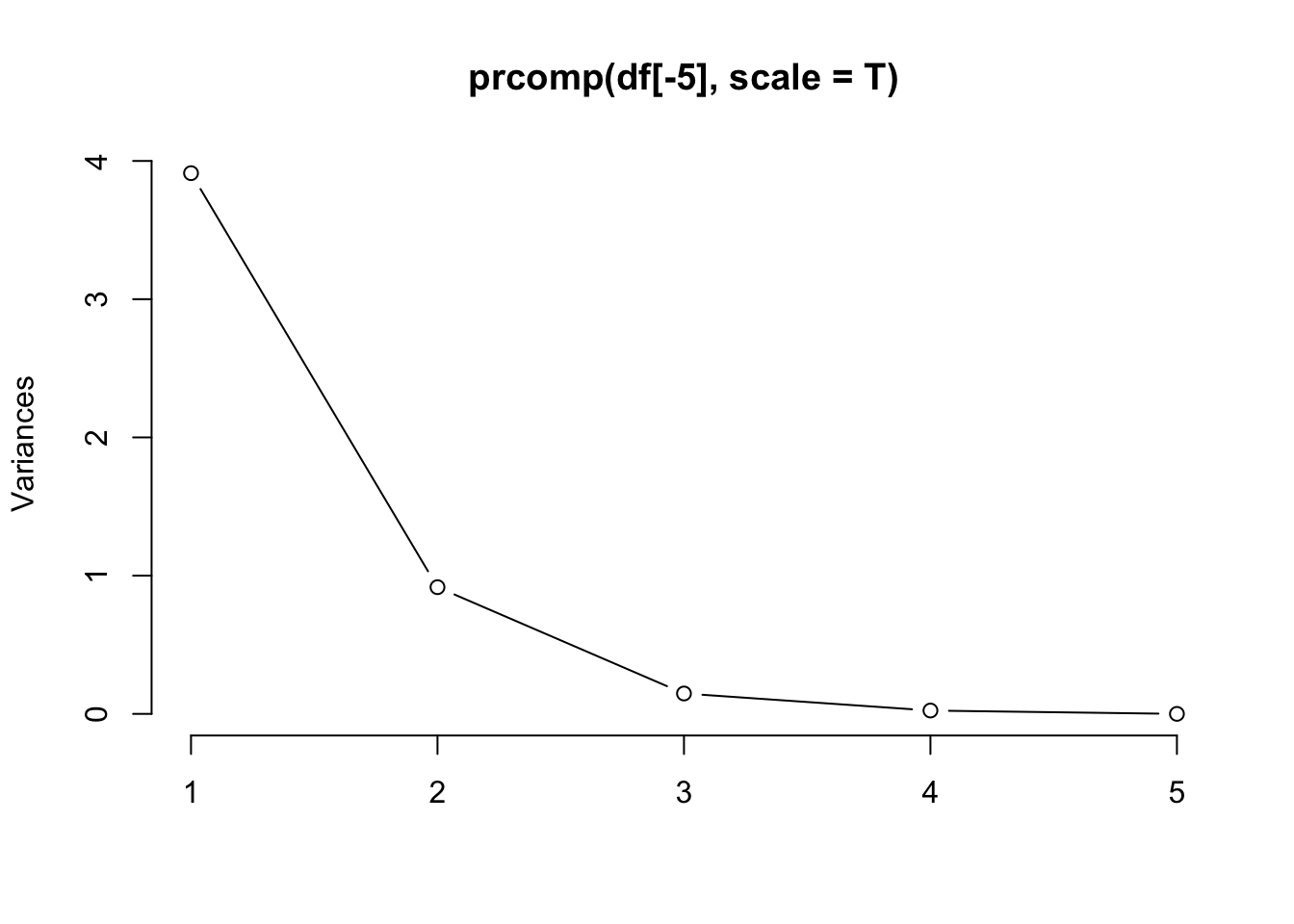.005702e-16

screeplot(prcomp(df[-5], scale = T), type = 'lines')

Exemplo 9.2 Considere o banco de dados iris, que contém 4 colunas numéricas com as larguras e comprimentos das pétalas e sépalas de três espécies de lírio (iris).

head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

Existem \({4 \choose 2} = 6\) combinações possíveis de gráficos bidimensionais, apresentados a seguir.

require(gridExtra)
p1 <- ggplot(iris, aes(Sepal.Length, Sepal.Width, colour = Species)) + geom_point()
p2 <- ggplot(iris, aes(Sepal.Length, Petal.Length, colour = Species)) + geom_point()
p3 <- ggplot(iris, aes(Sepal.Length, Petal.Width, colour = Species)) + geom_point()
p4 <- ggplot(iris, aes(Sepal.Width, Petal.Length, colour = Species)) + geom_point()
p5 <- ggplot(iris, aes(Sepal.Width, Petal.Width, colour = Species)) + geom_point()
p6 <- ggplot(iris, aes(Petal.Length, Petal.Width, colour = Species)) + geom_point()
grid.arrange(p1, p2, p3, p4, p5, p6, ncol = 2)

É posível utilizar o método de componentes principais para aprimorar a visualização¹⁰ da estrutura de associação entre as diferentes espécies de plantas.

library(ggfortify)
autoplot(prcomp(df[-5]), data = iris, colour = 'Species', 
         loadings = T, loadings.label = T, type = 'raw')

autoplot(prcomp(df[-5], scale = T), data = iris, colour = 'Species', 
         loadings = T, loadings.label = T)

Exercício 9.1 Considere o banco de dados sobre câncer de mama apresentado por (Dua and Graff 2019). A partir do código abaixo, faça uma anáise de componentes principais desconsiderando as duas primeiras colunas, que indicam respectivamente o código de identificação da paciente (V1) e o diagnóstico (V2, Benigno/Maligno).
(a) Quais os valores de \(n\) e \(p\)?
(b) O que ocorre no comando x2 <- x[,-c(1,2)]?
(c) Obtenha os autovalores e autovetores.
(d) Apresente o screeplot.
(e) Apresente o gráfico dos dois primeiros componentes principais colorido por V2.
(f) Você considera que é possível associar os diagnósticos às variáveis V3 a V32? Dica: observe se há algum tipo de agrupamento no gráfico do item (e).
(g) Quais variáveis mais influenciam nos compomentes principais 1 e 2? Dica: use loadings.label = T na função autoplot do item (e) e observe o gráfico.

library(ggfortify)
x <- read.table('https://filipezabala.com/data/wdbc.data', sep = ',')
x2 <- x[,-c(1,2)]

Exercício 9.2 Faça a análise de componentes principais considerando o banco de dados apresentado por (Fokoue 2020). Considere o código a seguir.

tf <- paste0(tempfile(), '.zip')
url0 <- 'https://archive.ics.uci.edu/static/public/518/speaker+accent+recognition.zip'
download.file(url0, tf)
unzip(tf, list = TRUE)
dt <- read.csv(unzip(tf, 'accent-mfcc-data-1.csv'))
summary(dt)
str(dt)
pc <- prcomp(dt[-1])
library(ggfortify)
autoplot(pc, data = dt, colour = 'language',
         loadings = T, loadings.label = T, type = 'raw')

Exercício 9.3 Faça a análise de componentes principais considerando o banco de dados robCompositions::arcticLake.

pc <- prcomp(robCompositions::arcticLake)

Referências

Bishop, Christopher M. 1999. “Bayesian PCA.” In Advances in Neural Information Processing Systems, 382–88. https://papers.nips.cc/paper/1549-bayesian-pca.pdf.

Cattell, Raymond B. 1966. “The Scree Test for the Number of Factors.” Multivariate Behavioral Research 1 (2): 245–76. https://doi.org/10.1207/s15327906mbr0102_10.

Dua, Dheeru, and Casey Graff. 2019. “UCI Machine Learning Repository.” University of California, Irvine, School of Information; Computer Sciences. http://archive.ics.uci.edu/ml.

Fokoue, E. 2020. “Speaker Accent Recognition Data Set.” University of California, Irvine, School of Information; Computer Sciences. https://archive.ics.uci.edu/ml/datasets/Speaker+Accent+Recognitions.

———. 1933. “Analysis of a Complex of Statistical Variables into Principal Components.” Journal of Educational Psychology 24 (6): 417. https://psycnet.apa.org/fulltext/1934-00645-001.pdf.

Pearson, Karl. 1901. “On Lines and Planes of Closest Fit to Systems of Points in Space.” Philosophical Magazine 2 (11): 559–72. http://pca.narod.ru/pearson1901.pdf.

---

10. Exemplos baseados em https://cran.r-project.org/web/packages/ggfortify/vignettes/plot_pca.html.↩︎