4.2 Gráficos multivariados

There is no statistical tool that is as powerful as a well-chosen graph. (John M. Chambers et al. 1998, 1)

Exercício 4.4 Veja:

  1. Visualização de Fundamentos de Estatística.
  2. Fienberg (1979), https://www.sci.utah.edu/~kpotter/Library/Papers/fienberg:1979:GMIS/index.html.

Recomenda-se a leitura da seção de .

4.2.1 Matriz de dispersão

pairs(mtcars[,-c(8,9)])  # desconsiderando vs e am

4.2.2 Correlograma

Adaptado de http://www.r-graph-gallery.com/97-correlation-ellipses/.

# Bibliotecas
library(ellipse)
library(RColorBrewer)

# Usando o famoso banco de dados 'mtcars'
R <- cor(mtcars[,-c(8,9)])

# Painel de 100 cores com Rcolor Brewer
my_colors <- brewer.pal(5, "Spectral")
my_colors <- colorRampPalette(my_colors)(100)

# Ordenando a matriz de correlação
ord <- order(R[1, ])
R_ord <- R[ord, ord]
plotcorr(R_ord , col=my_colors[R_ord*50+50] , mar=c(1,1,1,1))

Adaptado de http://r-statistics.co/Top50-Ggplot2-Visualizations-MasterList-R-Code.html#Correlogram.

# Bibliotecas
library(ggplot2)
library(ggcorrplot)

# Matriz de correlação
data(mtcars)
R <- round(cor(mtcars[,-c(8,9)]), 1)

# Gráfico
ggcorrplot(R, hc.order = TRUE,
           type = 'lower',
           lab = TRUE,
           lab_size = 3,
           method = 'circle',
           colors = c('tomato2', 'white', 'springgreen3'),
           title = 'Correlograma de mtcars',
           ggtheme = theme_bw)

Exercício 4.5 Considere o banco de dados iris. a. Obtenha as medidas-resumo média e matriz de covariância das variáveis numéricas. b. Apresente os resultados de forma gráfica.

4.2.3 Boxplot bivariado (bagplot)

(Goldberg and Iglewicz 1992) e (Rousseeuw, Ruts, and Tukey 1999) discutem métodos para construir generalizações bivariadas do boxplot. A implementação em R de (Signorell 2024) é baseada em (Rousseeuw, Ruts, and Tukey 1999), e conforme a documentação “[n]o caso bivariado a caixa do boxplot muda para um polígono convexo, a bolsa (bag) do bagplot”, onde estão 50% de todos os pontos. A cerca (fence) é calculada aumentando a bolsa, e separa os pontos internos e externos. O loop é definido como o invólucro convexo (Seção 4.2.3.1) contendo todos os pontos dentro da cerca.

set.seed(1); dat <- cbind(rnorm(100) + 100, rnorm(100) + 300)
dat <- rbind(dat, c(105,295))
DescTools::PlotBag(dat)

Exercício 4.6 Veja as seguintes documentações:

  1. ?DescTools::PlotBag.
  2. (Wickham and Stryjewski 2011).

4.2.3.1 Invólucro convexo

De acordo com (B. Everitt 2005, 22), “o invólucro convexo4 de um conjunto de observações bivariadas consiste nos vértices do menor poliedro convexo no espaço variável dentro do qual, ou no qual, todos os pontos de dados se encontram. A remoção dos pontos situados no casco convexo pode eliminar valores discrepantes isolados sem perturbar a forma geral da distribuição bivariada. Uma estimativa robusta do coeficiente de correlação resulta da utilização das observações restantes”.

Para uma abordagem em três dimensões, veja (Preparata and Hong 1977).

# Create a set of random data to plot convex hull around
x <- rnorm(100,0.8,0.3)
y <- rnorm(100,0.8,0.3)

#get max and min of all x and y data for nice plotting
xrange <- range(x)
yrange <- range(y)

#plot it up!
plot(x,y,type="p",pch=1,col='black',xlim=c(xrange),ylim=c(yrange))
BMhyd::Plot_ConvexHull(xcoord=x,ycoord=y,lcolor='red')

Exercício 4.7 Veja o artigo disponível em https://medium.com/@pascal.sommer.ch/a-gentle-introduction-to-the-convex-hull-problem-62dfcabee90c

4.2.4 Gráfico qui

Gráficos qui (N. I. Fisher and Switzer 1985), (N. I. Fisher and Switzer 2001) fornecem um método para diagnosticar dependência multivariada entre \(Y\) variáveis. São gráficos de dispersão dos pares \((\lambda_i, \chi_i)\) onde

\[\begin{equation} \chi_i = \frac{H_i-F_i G_i}{\sqrt{F_i (1-F_i) G_i (1-G_i)}} \tag{4.28} \end{equation}\]

\[\begin{equation} \lambda_i = 4 S_i \max \left\{ \left( F_i - \frac{1}{2} \right)^2, \left( G_i - \frac{1}{2} \right)^2 \right\} \tag{4.29} \end{equation}\]

\[\begin{equation} H_i = \sum_{j \ne i} \frac{I(x_j \le x_i, y_j \le y_i)}{n-1} \tag{4.30} \end{equation}\]

\[\begin{equation} F_i = \sum_{j \ne i} \frac{I(x_j \le x_i)}{n-1} \tag{4.31} \end{equation}\]

\[\begin{equation} G_i = \sum_{j \ne i} \frac{I(y_j \le y_i)}{n-1} \tag{4.32} \end{equation}\]

\[\begin{equation} S_i = \mathop{\mathrm{sign}}\left\{ \left( F_i - \frac{1}{2} \right) \left( G_i - \frac{1}{2} \right) \right\} \tag{4.33} \end{equation}\]

onde \(I(A)\) é a função indicadora do evento \(A\), sendo igual a 1 de \(A\) é verdadeira e 0 caso contrário. \(\mathop{\mathrm{sign}}(x)\) é igual a \(+1\) se \(x>0\), 0 se \(x=0\) e \(-1\) se \(x<0\). Quando as variáveis avaliadas são independentes, os pontos devem estar distribuídos dentro das bandas calculadas; quando forem dependentes, devem-se observar pontos fora das bandas.

Exemplo 4.6 Considere o gráfico de 5 pontos sequenciais de correlação 1.

library(asbio)
x <- 1:5
y <- 1:5
plot(x,y)

asbio::chi.plot(x,y, main = 'Pontos acima das bandas')

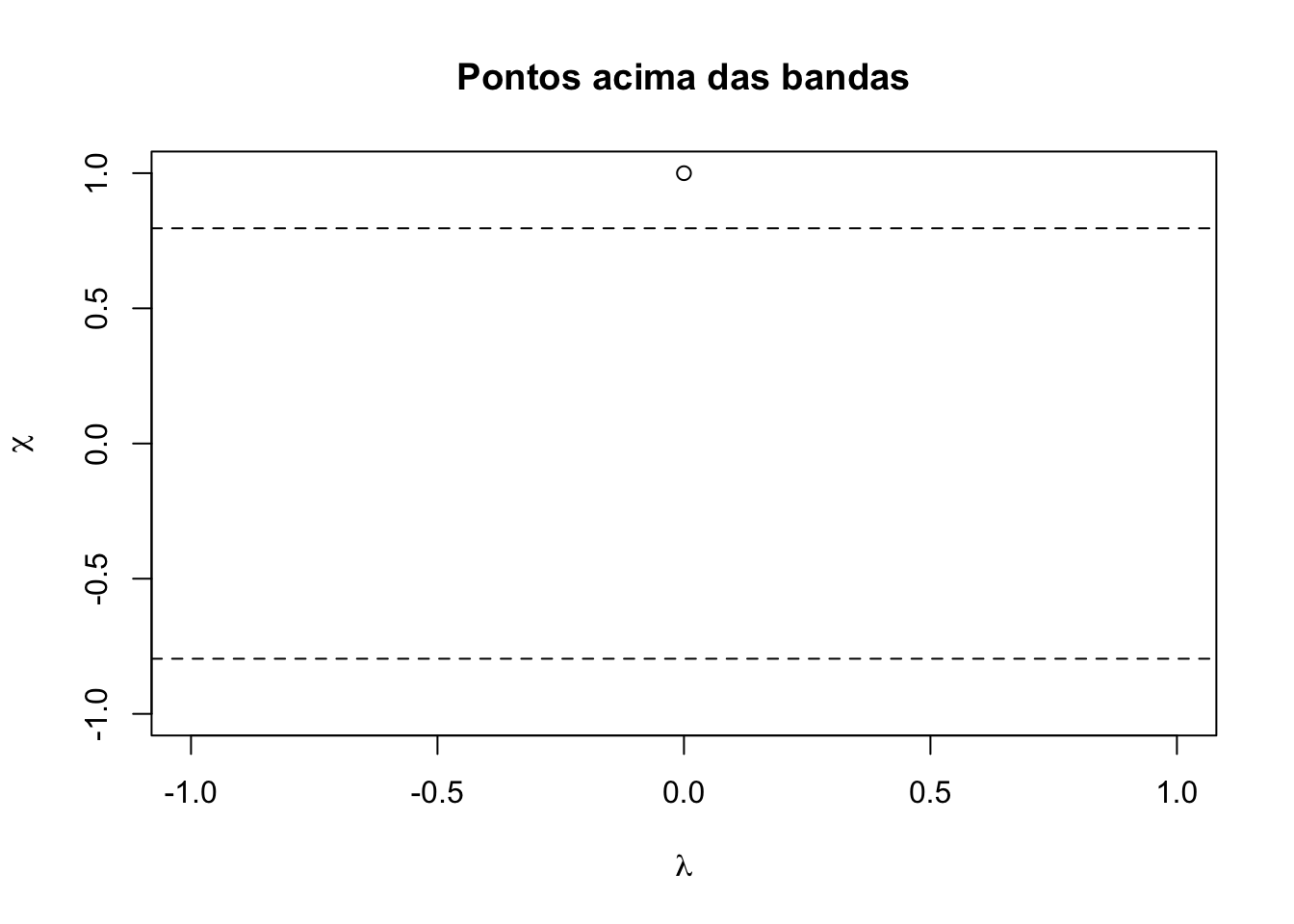
Exemplo 4.7 Considere os gráficos a seguir, inspirados no exemplo da documentação de asbio::chi.plot.

library(asbio)
library(mvtnorm)
# X simulado com correlação 0.9
set.seed(1); X <- mvtnorm::rmvnorm(100, mean = c(15,18), 
                                   sigma = matrix(c(2^2, 0.9*2*3.2,
                                                    0.9*2*3.2, 3.2^2), nrow = 2))
# Y simulado com correlação 0
set.seed(2); Y <- mvtnorm::rmvnorm(100, mean = c(15,18), 
                                   sigma = matrix(c(2^2, 0,
                                                    0, 3.2^2), nrow = 2))
# gráficos
par(mfrow=c(2,2))
plot(X[,1], X[,2], main = 'Correlação 0.9')
asbio::chi.plot(X[,1], X[,2], main = 'Pontos acima das bandas')

plot(Y[,1], Y[,2], main = 'Correlação 0')
asbio::chi.plot(Y[,1], Y[,2], main = 'Pontos dentro das bandas')

Exercício 4.8 Considere os dados do Exemplo ??.
a. Por que os elementos da diagonal principal de \(\Sigma\) estão elevados ao quadrado?
b. A partir da Eq. (4.23) verifique por que a diagonal secundária da matriz \(\Sigma\) de \(X\) é dada por 0.9*2*3.2.
c. Crie uma variável \(Z\) com correlação -0.7 e analise seu gráfico qui.

4.2.5 The Grand Tour

The idea of the grand tour is to move through a sequence of projections, chosen to be dense in the set of all projections. (Asimov 1985, 1)

(Asimov 1985) apresenta o Grand Tour, método para visualizar dados estatísticos multivariados por meio de projeções ortogonais em uma sequência de subespaços bidimensionais. Exemplos de aplicação podem ser encontrados no pacote Pursuit de (Ossani and Cirillo 2021), detalhado na Seção 8.5.

library(Pursuit)

inter <- GrandTour(iris[,1:4], method = "Interpolation", title = "Torus", xlabel = NA, ylabel = NA,
                 color = TRUE, linlab = NA, posleg = 2, boxleg = FALSE, axesvar = FALSE,
                 axes = FALSE, numrot = 1, choicerot = NA, class = iris[,5],
                 classcolor = c("goldenrod3","gray53","red"),savptc = FALSE,
                 width = 3236, height = 2000, res = 300)

# plot(inter$proj.data, main = inter$method)

torus <- GrandTour(iris[,1:4], method = "Torus", title = "Torus", xlabel = NA, ylabel = NA,
                 color = TRUE, linlab = NA, class = NA, posleg = 2, boxleg = TRUE,
                 axesvar = TRUE, axes = FALSE, numrot = 1, choicerot = NA,
                 savptc = FALSE, width = 3236, height = 2000, res = 300)

# plot(torus$proj.data, main = torus$method)

pseudo <- GrandTour(iris[,1:4], method = "Pseudo", title = "Pseudo", xlabel = NA, ylabel = NA,
                 color = TRUE, linlab = NA, class = NA, posleg = 2, boxleg = TRUE,
                 axesvar = TRUE, axes = FALSE, numrot = 1, choicerot = NA,
                 savptc = FALSE, width = 3236, height = 2000, res = 300)

# plot(pseudo$proj.data, main = pseudo$method)

4.2.6 Chernoff Faces

Chernoff (1973) apresenta um método gráfico de representação de pontos em um espaço \(k\)-dimensional (\(k \le 18\)) através de um desenho de um rosto através de características, tais como tamanho do nariz e curvatura da boca. Wolf (2019) apresenta a biblioteca aplpack, que traz uma implementação do método de Chernoff.

library(aplpack)
faces()
## effect of variables:
##  modified item       Var   
##  "height of face   " "Var1"
##  "width of face    " "Var2"
##  "structure of face" "Var3"
##  "height of mouth  " "Var1"
##  "width of mouth   " "Var2"
##  "smiling          " "Var3"
##  "height of eyes   " "Var1"
##  "width of eyes    " "Var2"
##  "height of hair   " "Var3"
##  "width of hair   "  "Var1"
##  "style of hair   "  "Var2"
##  "height of nose  "  "Var3"
##  "width of nose   "  "Var1"
##  "width of ear    "  "Var2"
##  "height of ear   "  "Var3"

data(longley)
plot(longley[1:16,2:3], bty='n')
a <- faces(longley[1:16,], plot=FALSE)
## effect of variables:
##  modified item       Var           
##  "height of face   " "GNP.deflator"
##  "width of face    " "GNP"         
##  "structure of face" "Unemployed"  
##  "height of mouth  " "Armed.Forces"
##  "width of mouth   " "Population"  
##  "smiling          " "Year"        
##  "height of eyes   " "Employed"    
##  "width of eyes    " "GNP.deflator"
##  "height of hair   " "GNP"         
##  "width of hair   "  "Unemployed"  
##  "style of hair   "  "Armed.Forces"
##  "height of nose  "  "Population"  
##  "width of nose   "  "Year"        
##  "width of ear    "  "Employed"    
##  "height of ear   "  "GNP.deflator"
plot.faces(a, longley[1:16,2], longley[1:16,3], width=35, height=30)

References

Asimov, Daniel. 1985. “The Grand Tour: A Tool for Viewing Multidimensional Data.” SIAM Journal on Scientific and Statistical Computing 6 (1): 128–43. https://doi.org/10.1137/0906011.
Chambers, John M, William S Cleveland, Beat Kleiner, and Paul A Tukey. 1998. Graphical Methods for Data Analysis. 2nd ed. Chapman; Hall/CRC. https://www.taylorfrancis.com/books/mono/10.1201/9781351072304/graphical-methods-data-analysis-chambers.
Chernoff, Herman. 1973. “The Use of Faces to Represent Points in k-Dimensional Space Graphically.” Journal of the American Statistical Association 68 (342): 361–68. https://www.stat.cmu.edu/~rnugent/PCMI2016/papers/ChernoffFaces.pdf.
Everitt, Brian. 2005. An r and s-PLUS Companion to Multivariate Analysis. Springer.
Fienberg, Stephen E. 1979. “Graphical Methods in Statistics.” The American Statistician 33 (4): 165–78. https://doi.org/10.2307/2683729.
Fisher, N. I., and P. Switzer. 1985. “Chi-Plots for Assessing Dependence.” Biometrika 72 (2): 253–65. https://www.jstor.org/stable/2336078.
———. 2001. “Graphical Assessment of Dependence: Is a Picture Worth 100 Tests?” The American Statistician 55 (3): 233–39. https://doi.org/10.1198/000313001317098248.
Goldberg, Kenneth M, and Boris Iglewicz. 1992. “Bivariate Extensions of the Boxplot.” Technometrics 34 (3): 307–20. https://www.jstor.org/stable/1270037.
Ossani, Paulo Cesar, and Marcelo Angelo Cirillo. 2021. Projection Pursuit. https://CRAN.R-project.org/package=Pursuit.
Preparata, Franco P., and Se June Hong. 1977. “Convex Hulls of Finite Sets of Points in Two and Three Dimensions.” Communications of the ACM 20 (2): 87–93. https://dl.acm.org/doi/pdf/10.1145/359423.359430.
Rousseeuw, Peter J, Ida Ruts, and John W Tukey. 1999. “The Bagplot: A Bivariate Boxplot.” The American Statistician 53 (4): 382–87. https://wis.kuleuven.be/statdatascience/robust/papers/1999/rousseeuwrutstukey-bagplot-amerstat-1999-bw.pdf.
Signorell, Andri. 2024. DescTools: Tools for Descriptive Statistics. https://CRAN.R-project.org/package=DescTools.
Wickham, Hadley, and Lisa Stryjewski. 2011. “40 Years of Boxplots.” The American Statistician, 17. https://vita.had.co.nz/papers/boxplots.html.
Wolf, Hans Peter. 2019. aplpack: Another Plot Package (Version 190512). https://cran.r-project.org/package=aplpack.

  1. The convex hull of a set of bivariate observations consists of the vertices of the smallest convex polyhedron in variable space within which, or on which, all data points lie. Removal of the points lying on the convex hull can eliminate isolated outliers without disturbing the general shape of the bivariate distribution. A robust estimate of the correlation coefficient results from using the remaining observations.↩︎