6.1 Teste para um vetor média
6.1.1 Caso univariado, \(p=1\)
Pode-se testar \(H_0: \mu = \mu_0\) vs \(H_1: \mu \ne \mu_0\) supondo \(H_0\) verdadeira (sob \(H_0\)) utilizando a estatística de teste7 \[\begin{equation} t_0 = \frac{\bar{x}-\mu_0}{s/\sqrt{n}} \sim t_{n-1} \tag{6.1} \end{equation}\]
i.e., \(t_0\) possui distribuição \(t\) de Student com \(n-1\) graus de liberdade. A média amostral pode ser calculada por \(\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i\) e o desvio padrão amostral pode ser obtido por \(s = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_{i} - \bar{x})^2}\).
É conhecida também a relação \(t_{0}^2 \sim F_{1,n-1}\), onde \(F_{1,n-1}\) indica a distribuição \(F\) de Snedecor com 1 grau de liberdade no numerador e \(n-1\) graus de liberdade no denominador. Assim,
\[\begin{equation} t_0^2 = \left( \frac{\bar{x}-\mu_0}{s/\sqrt{n}} \right)^2 = n (\bar{x}-\mu_0) (s^2)^{-1} (\bar{x}-\mu_0)\sim F_{1,n-1} \tag{6.2} \end{equation}\]
Exemplo 6.1 Pode-se realizar o teste t univariado de diversas formas.
## [1] -2 -1 0 1 2 3 4 5## [1] 8## [1] 1.5## [1] 2.44949## [1] 1.732051## [1] 0.1268704## [1] 0.1268704##
## One Sample t-test
##
## data: x
## t = 1.7321, df = 7, p-value = 0.1269
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.5478247 3.5478247
## sample estimates:
## mean of x
## 1.5Exercício 6.1 Considere o conjunto de dados disponível neste link, onde filhos e altura indicam o número de filhos e a altura de mulheres em um exemplo hipotético. Resolva os itens a seguir utilizando a ferramenta da sua preferência considerando \(\alpha=0.05\).
(a) Faça o teste de hipóteses apropriado para verificar se o número médio de filhos pode ser considerado igual a 2.3, i.e., \(H_0: \mu = 2.3\).
(b) Faça o teste de hipóteses apropriado para verificar se a altura média pode ser considerada igual a 1.62, i.e., \(H_0: \mu = 1.62\).
6.1.2 Caso multivariado, \(p>1\)
(Hotelling 1931) propôs uma generalização para o caso multivariado (\(p>1\)) para testar \(H_0: \boldsymbol{\mu} = \boldsymbol{\mu}_0\) vs \(H_1: \boldsymbol{\mu} \ne \boldsymbol{\mu}_0\) (um grupo) ou ainda \(H_0: \boldsymbol{\mu}_1 = \boldsymbol{\mu}_2\) vs \(H_1: \boldsymbol{\mu}_1 \ne \boldsymbol{\mu}_2\) (dois grupos).
Para o caso de um grupo, sob \(H_0\) \[\begin{equation} T_0^2 = n (\bar{\boldsymbol{x}}-\boldsymbol{\mu}_0)' \boldsymbol{S}^{-1} (\bar{\boldsymbol{x}}-\boldsymbol{\mu}_0) \sim \frac{(n-1)p}{n-p}F_{p,n-p} \tag{6.3} \end{equation}\]
Para o caso de dois grupos (de tamanhos \(n_1\) e \(n_2\)), sob \(H_0\) \[\begin{equation} T_0^2 = \frac{n_1+n_2-p-1}{(n_1+n_2-2)p} \frac{n_1 n_2}{n_1+n_2} (\bar{\boldsymbol{x}}-\bar{\boldsymbol{y}})' \boldsymbol{S}^{-1} (\bar{\boldsymbol{x}}-\bar{\boldsymbol{y}}) \sim F_{p,n_1+n_2-1-p} \tag{6.4} \end{equation}\]
Exemplo 6.2 (R. A. Johnson and Wichern 1998, 229) analisaram a transpiração de 20 mulheres saudáveis. Três componentes foram medidos e os resultados estão disponiveis neste link.
- X1: taxa de suor (sweat)
- X2: teor de sódio (sodium)
- X3: teor de potássio (potassium)
Deseja-se testar \(H_0: \boldsymbol{\mu} = \begin{bmatrix} 4 \\ 50 \\ 10 \end{bmatrix}\) vs \(H_1: \boldsymbol{\mu} \ne \begin{bmatrix} 4 \\ 50 \\ 10 \end{bmatrix}\) utilizando \(\alpha = 0.1\). Sob \(H_0\) pode-se utilizar a Eq. (6.3).
# Fazendo todas a contas
sweat <- read.table('https://filipezabala.com/data/sweat.txt', header = T)
(alpha <- 0.1) # alpha (nível de significância)## [1] 0.1## [1] 20## [1] 3## sweat sodium potassium
## 4.640 45.400 9.965## sweat sodium potassium
## sweat 2.879368 10.0100 -1.809053
## sodium 10.010000 199.7884 -5.640000
## potassium -1.809053 -5.6400 3.627658## sweat sodium potassium
## sweat 0.58615531 -0.022085719 0.257968742
## sodium -0.02208572 0.006067227 -0.001580929
## potassium 0.25796874 -0.001580929 0.401846765mu0 <- c(4,50,10) # vetor sendo testado (sob H0)
(T0 <- n * t(m-mu0) %*% inv_S %*% (m-mu0)) # estatística do teste, Eq. (4.3)## [,1]
## [1,] 9.738773## [1] 3.352941## [1] 8.172573## [,1]
## [1,] 2.904546## [,1]
## [1,] 0.06492834curve(f*df(x,p,n-p), 0, 10) # gráfico rápido de f*F(3,17)
abline(v = vc, col = 'red') # corte no valor crítico
curve(df(x,p,n-p), 0, 10) # gráfico rápido de F(3,17)
abline(v = vc/f, col = 'red') # corte no valor crítico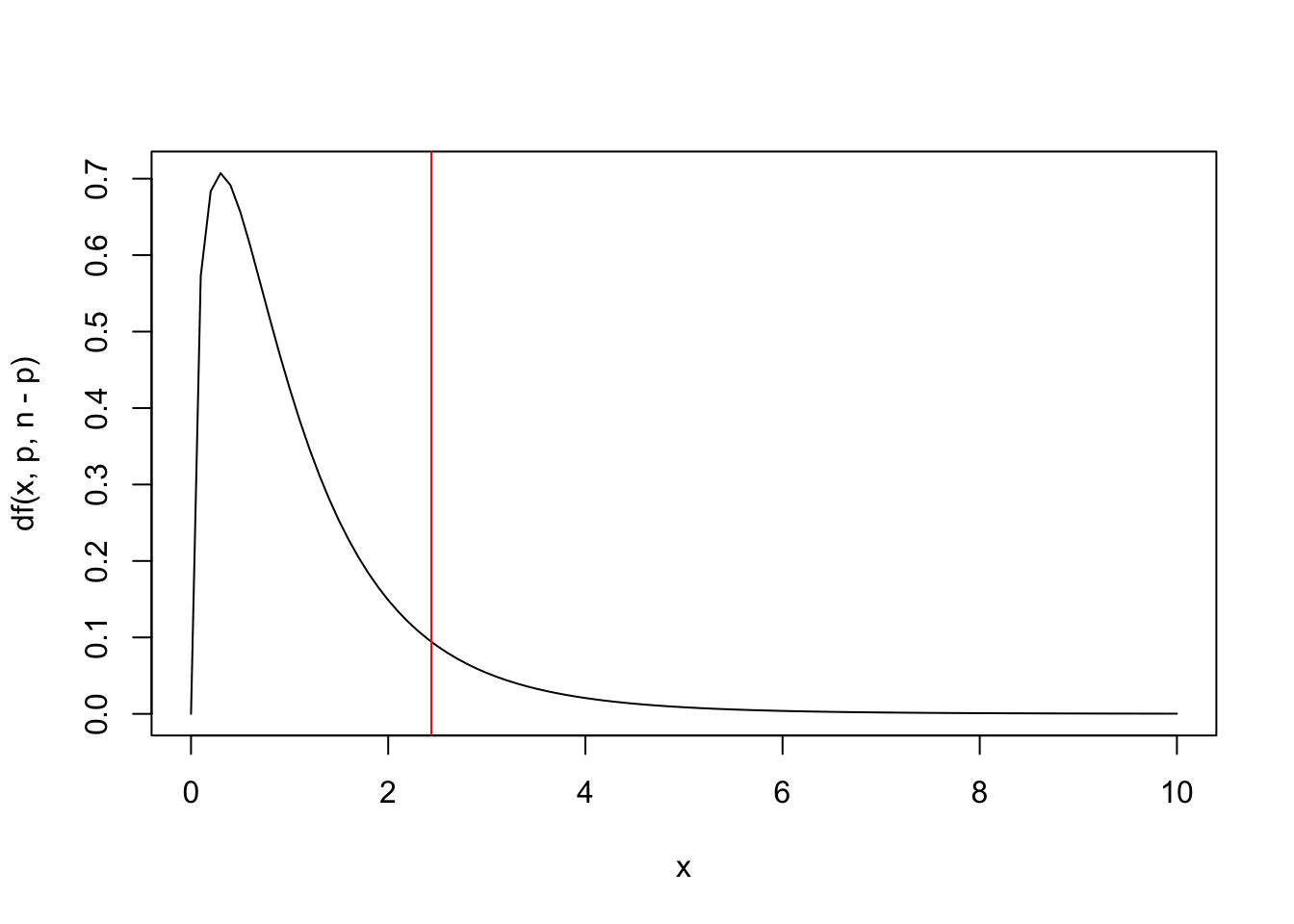
Exemplo 6.3 Pode-se resolver o Exemplo 6.2 utilizando a função ICSNP::HotellingsT2.
# Via ICSNP::HotellingsT2
sweat <- read.table('https://filipezabala.com/data/sweat.txt', header = T)
ICSNP::HotellingsT2(sweat, mu = c(4,50,10))##
## Hotelling's one sample T2-test
##
## data: sweat
## T.2 = 2.9045, df1 = 3, df2 = 17, p-value = 0.06493
## alternative hypothesis: true location is not equal to c(4,50,10)# gráfico da densidade da F(3,17) via ggplot2
library(ggplot2)
ggplot(data.frame(x = 0:10), aes(x, alpha = 0.05)) +
stat_function(fun = stats::df, args = c(3,17), geom = 'area',
xlim = c(qf(1-alpha, p, n-p), 10), fill = 'lightgreen') +
stat_function(fun = stats::df, args = c(3,17), show.legend = FALSE) +
xlab('x') + ylab('Densidade') +
theme(legend.position = 'none')
References
Também conhecida como pivô ou quantidade pivotal, uma função dos dados e parâmetros não observáveis tais que sua distribuição de probabilidades não dependa de parâmetros desconhecidos.↩︎