11.3 Métodos não hierárquicos (de particionamento)
11.3.1 K-médias
K-médias (k-means) é um nome genérico para métodos derivados dos algoritmos de (Lloyd 1957), (Forgy 1965), (MacQueen 1967), (Hartigan 1975) e (Hartigan and Wong 1979). A ideia básica é encontrar grupos similares, de maneira a minimizar a soma de distâncias euclidianas ao quadrado. As distâncias são calculadas entre os pontos e as médias de cada um dos \(k\) grupos, chamadas centróides.
Em relação ao modo de busca podem ser classificados como algoritmos de comutação, em que objetos devem ser particionados em \(k\) de grupos. Uma partição inicial é dada de forma arbitrária, onde se definem \(k\) centróides. Calcula-se a distância euclidiana ao quadrado entre as observações e os \(k\) centróides. O centróide mais próximo define o grupo ao qual uma observação pertence. Recalculam-se os novos centróides, e novas partições são obtidas com a alternância dos objetos entre os grupos. O algoritmo encerra quando nenhuma comutação adicional reduz a soma de quadrados intra-grupo, ou quando outro critério de parada é atingido.
São algoritmos relativamente rápidos na execução, mas são afetados pela incerteza da partição inicial. Há sempre a possibilidade de que partições iniciais distintas possam levar a partições finais superiores a outras.
A variação quadrática intra-grupo (\(VQI_{j}\)) do \(j\)-ésimo grupo é dada pela Equação (11.4). \[\begin{equation} VQI_{j} = \sum_{x_i \in G_j} (x_i - \mu_j)^2 \tag{11.4} \end{equation}\]
- \(x_i\) é o \(i\)-ésimo elemento pertencente ao grupo \(G_j\)
- \(\mu_j\) é o ponto médio do grupo \(G_j\)
- \(j \in \{2, \ldots, k\}\)
A soma de quadrados total (\(SQT\)) é dada pela Equação (11.5). \[\begin{equation} SQT = \sum_{i=1}^{k} VQI_{i} \tag{11.5} \end{equation}\]
Cada observação \(x_i\) é atribuída a um grupo de forma que a \(SQT\) seja mínima a cada iteração. É recomendado que seja feita a padronização dos dados, de maneira a controlar o impacto da escala na definição dos grupos.
ALGORITMO DAS K-MÉDIAS
PASSO 1 Especifique o número \(k\) de grupos a serem criados.
PASSO 2 Selecione arbitrariamente \(k\) pontos como centros dos grupos (centróides).
PASSO 3 Atribua cada observação ao grupo de centróide mais próximo, baseado na distância euclidiana entre a observação e os centróides.
PASSO 4 Recalcule os centróides com os pontos atribuídos a cada grupo. O centróide do \(j\)-ésimo grupo é um vetor de comprimento \(p\) contendo as médias das \(p\) variáveis, calculadas com todos os pontos atribuídos ao \(j\)-ésimo grupo.
PASSO 5 Repita os passos 3 e 4 até que as atribuições não mais reduzam a soma de quadrados intra-grupo, ou que o número máximo de iterações (ou qualquer outro critério de parada) seja atingido.
Seleção inicial dos centróides
(Hartigan 1975) sugere que a seleção inicial dos centróides seja baseada na soma dos casos \(S\), que tem um valor mínimo \(minS\) e um máximo \(maxS\). Para obter \(k\) grupos iniciais, propõe atribuir o \(i\)-ésimo caso ao \(j\)-ésimo grupo, onde \(j\) é a parte inteira de
\[\begin{equation} k \left( \dfrac{S-minS}{maxS-minS} \right) + 1 \tag{11.6} \end{equation}\]
Uma adaptação será feita, multiplicando 1.01 a \(maxS\) para evitar encontrar \(j>k\).
iris2 <- scale(iris[-5])
S <- rowSums(iris2)
k <- 2
zab <- k*(S - min(S))/(1.01*max(S)-min(S)) + 1 # atribuição de Zabala (2019) baseada em Hartigan (1975)
(g <- floor(zab)) # grupos## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 2 1 2 1 2 1 1
## [62] 2 1 2 1 2 1 1 1 1 2 1 1 1 2 2 2 2 2 1 1 1 1 2 1 2 2 1 1 1 1 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1 2 2 2 2 2 1 2 2
## [123] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2## g
## 1 2
## 83 67## INDICES: 1
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## -0.70707156 0.03984126 -0.68805740 -0.70250780
## -----------------------------------------------------------------------------------------------
## INDICES: 2
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 0.87592447 -0.04935559 0.85236961 0.87027086## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :-1.86378 Min. :-2.4258 Min. :-1.5623 Min. :-1.4422
## 1st Qu.:-0.89767 1st Qu.:-0.5904 1st Qu.:-1.2225 1st Qu.:-1.1799
## Median :-0.05233 Median :-0.1315 Median : 0.3354 Median : 0.1321
## Mean : 0.00000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 0.67225 3rd Qu.: 0.5567 3rd Qu.: 0.7602 3rd Qu.: 0.7880
## Max. : 2.48370 Max. : 3.0805 Max. : 1.7799 Max. : 1.7064Exercício 11.5 Utilize a Equação (23) sem a correção de Zabala e observe o resultado em iris2.
\(\\\)
Exercício 11.6 Utilize a Equação (23) com a correção de Zabala para criar uma função que defina os centróides iniciais para um valor genérico \(k\) de grupos em uma base de dados numérica. Teste em iris2 e outros bancos de dados já trabalhados.
Implementando no R
No R pode-se utilizar a função stats::kmeans para definir os grupamentos através das k-médias. Por padrão, esta função utiliza 10 como valor padrão para o número máximo de iterações e inicia com \(k\) centróides aleatórios.
km <- function(dados,grupos){
k <- kmeans(dados,grupos)
print(table(iris$Species, k$cluster))
plot(dados, col=k$cluster)
}
km(iris2,2)##
## 1 2
## setosa 50 0
## versicolor 0 50
## virginica 0 50
##
## 1 2 3
## setosa 0 0 50
## versicolor 11 39 0
## virginica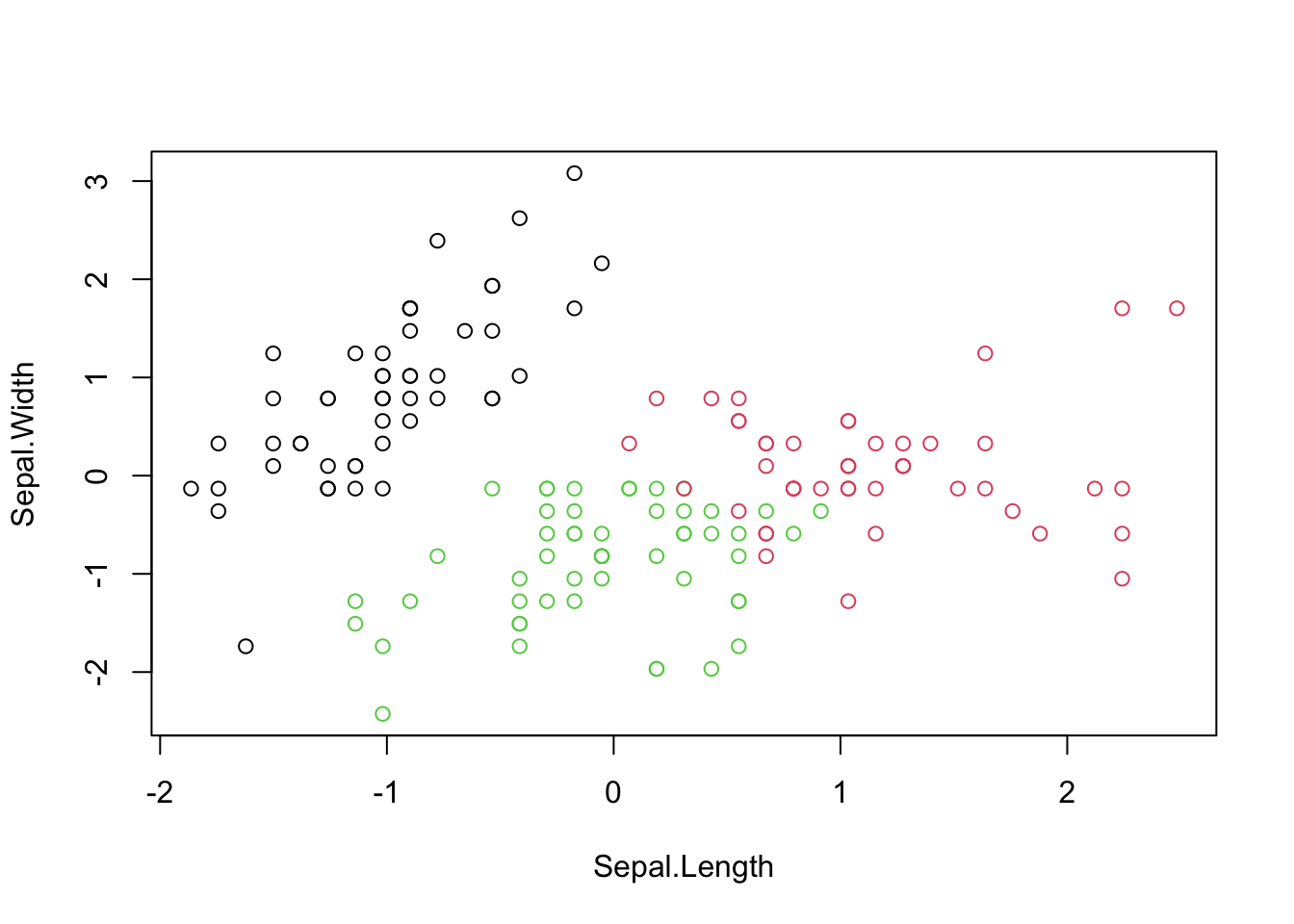 36 14 0
##
## 1 2 3 4
## setosa 0 49 0 1
## versicolor 2 0 29 19
## virginica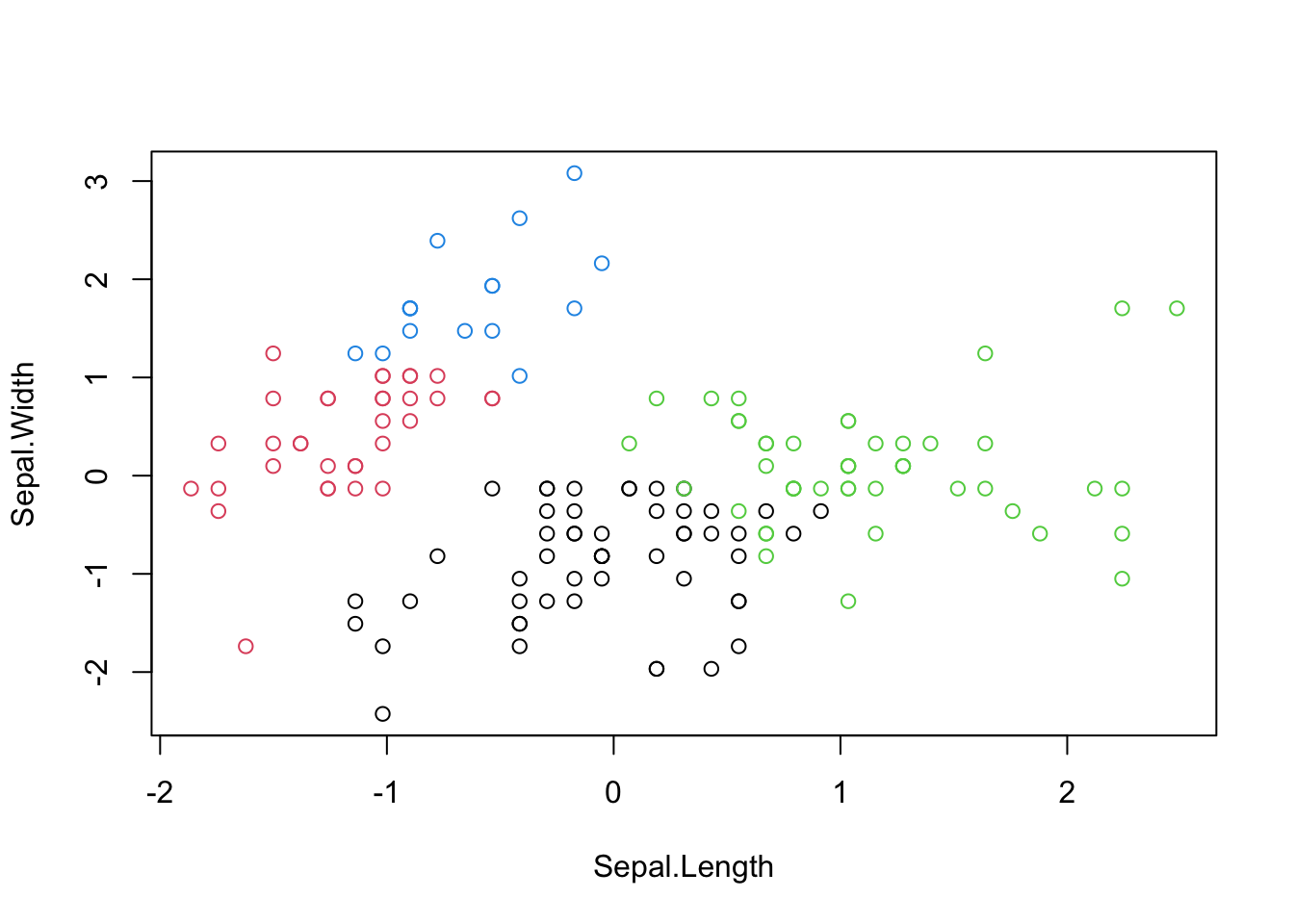 27 0 21 2
O pacote factoextra fornece uma série de melhorias para a análise de k-means. Além de gráficos mais sofisticados utilizando ggplot2, associa métodos hierárquicos e métodos de particionamento.
km2 <- function(dados,grupos){
k <- kmeans(dados,grupos)
fviz_cluster(k, iris2, repel = T)
}
km2(iris2,2)
Número de grupos
A função factoextra::fviz_nbclust fornece métodos para a escolha de um número ótimo de grupos. O método wss (total within sum of square), busca um número de grupos que traga um bom custo-benefício entre o número de grupos (\(k\)) e a soma de quadrados total (\(SQT\)). Este custo-benefício é indicado onde a curva muda sua declividade, ou no ‘cotovelo’ (elbow) ou ‘joelho’ (knee) do gráfico de \(k\) por \(SQT\). Tem suas origens no trabalho de (R. L. Thorndike 1953).
O método silhouette busca o número de grupos que maximize o tamanho médio da silhueta. É baseado em uma medida sugerida por (Rousseeuw and Kaufman 1990), dada por
\[\begin{equation} s(i) = \dfrac{b(i)-a(i)}{max\{ a(i),b(i) \}} \tag{11.7} \end{equation}\]
- \(-1 \le s(i) \le 1\)
- \(a(i)\): dissimilaridade média do elemento \(i\) em relação a todos os demais elementos do seu grupo \(A\)
- \(d(i,C)\): dissimilaridade média do elemento \(i\) em relação a todos os elementos do grupo \(C \ne A\)
- \(b(i) = \underset{C \ne A}{\mathrm{min}} \; d(i,C)\)
Proposto por (Tibshirani, Walther, and Hastie 2001), o método gap_stat (gap statistic) compara variação total intra-grupo para diferentes valores de k com seus valores esperados sob alguma distribuição de referência. A estimativa dos clusters ótimos será o valor que maximiza a estatística de gap (isto é, que gera a maior estatística de gap).
\[\begin{equation} \mathrm{Gap}_{n}(k) = E^{*} \{ \mathrm{log}(W_k) \} - \mathrm{log}(W_k) \tag{11.8} \end{equation}\]
- \(E^{*}\) é o valor esperado sob uma amostra de tamanho \(n\) da distribuição de referência
- \(W_k = \sum_{j=1}^{k} \dfrac{1}{2n_j} D_j\)
- \(D_j = \sum_{i,i' \in C_j} d_{ii'}\)
- \(n_j = |C_j|\)
## Clustering k = 1,2,..., K.max (= 10): .. done
## Bootstrapping, b = 1,2,..., B (= 100) [one "." per sample]:
## .................................................. 50
## .................................................. 100
11.3.2 K-medianas
Existem extensões do método de k-médias, utilizando medianas para fazer os grupamentos. O pacote Gmedian de (Cardot 2021) traz a função kGmedian, que realiza o agrupamento rápido de k-medianas com base em algoritmos de gradiente estocástico ponderado recursivo (Cardot, Cénac, and Monnez 2012), (Cardot et al. 2013). O procedimento é semelhante à técnica de agrupamento stats::kmeans realizada recursivamente com o algoritmo de (MacQueen 1967). A vantagem do algoritmo kGmedian em relação à estratégia de MacQueen é que ele lida com soma de normas ao invés de soma de normas quadradas, garantindo um comportamento mais robusto contra valores extremos (outliers).
library(Gmedian)
iris2 = scale(iris[-5])
cl.kmeans <- kmeans(iris2, 2)
cl.kmedian <- kGmedian(iris2, 2)
par(mfrow=c(1,2))
plot(iris2, col = cl.kmeans$cluster, main = 'kmeans')
points(cl.kmeans$centers, col = 1:2, pch = 8, cex = 2)
plot(iris2, col = cl.kmedian$cluster, main = 'kGmedian')
points(cl.kmedian$centers, col = 1:2, pch = 8, cex = 2)
11.3.3 K-medóides
https://www.datanovia.com/en/lessons/k-medoids-in-r-algorithm-and-practical-examples/
https://cran.r-project.org/web/packages/ClusterR/vignettes/the_clusterR_package.html
O algoritmo k-medóides proposto por (Kaufman and Rousseeuw 1987) é um algoritmo de particionamento relacionado ao algoritmo de k-médias. Assim como nas k-médias o objetivo é minimizar a distância entre os pontos e o centróide de um grupo. Ao contrário das k-médias o algoritmo dos k-medóides define necessariamente um ponto observado como centro.
11.3.4 k-modas
O algoritmo das k-modas executa o particionamento de dados categóricos. O pacote klaR (Weihs et al. 2005) traz a função kmodes baseada em (MacQueen 1967) e (Huang 1997).
library(klaR)
## generate data set with two groups of data:
set.seed(1)
x <- rbind(matrix(rbinom(250, 2, 0.25), ncol = 5),
matrix(rbinom(250, 2, 0.75), ncol = 5))
colnames(x) <- c('a', 'b', 'c', 'd', 'e')
## run algorithm on x:
(cl <- kmodes(x, 2))## K-modes clustering with 2 clusters of sizes 44, 56
##
## Cluster modes:
## a b c d e
## 1 1 2 1 0 2
## 2 2 0 2 1 0
##
## Clustering vector:
## [1] 2 2 2 2 2 1 2 1 1 1 1 2 1 2 2 2 1 1 2 1 2 2 2 2 1 2 2 2 2 1 1 1 2 1 1 1 2 2 2 2 2 1 1 2 1 2 2 2 1 1 2 1 1 1 1 2 1 2 1 1 1
## [62] 2 2 1 1 2 2 1 1 2 2 2 1 2 2 2 2 1 2 2 2 1 1 2 2 2 1 1 2 2 2 2 1 2 2 1 1 1 2 1
##
## Within cluster simple-matching distance by cluster:
## [1] 105 142
##
## Available components:
## [1] "cluster" "size" "modes" "withindiff" "iterations" "weighted"## and visualize with some jitter:
plot(jitter(x), col = cl$cluster)
points(cl$modes, col = 1:5, pch = 8)
11.3.5 ROCK
Assim como as k-modas, o algoritmo Rock executa o particionamento de dados categóricos. O pacote cba (Buchta and Hahsler 2019) traz a função rockCluster baseada em (Guha, Rastogi, and Shim 2000).
## Clustering:
## computing distances ...
## computing links ...
## computing clusters ...## data: x
## beta: 0.5
## theta: 0.5
## fun: dist
## args: list("binary")
## 1 2
## 96 4