2.1 Funções de variáveis aleatórias

Uma função de variável aleatória é uma transformação (função) de \(\mathbb{R}^n\) em \(\mathbb{R}^n\), denotada \(g:\mathbb{R}^n \rightarrow \mathbb{R}^n\).

Exemplo 2.1 Seja a variável aleatória \(X \sim \mathcal{U}(-1,1)\) e a função \(Y=X+2\). É possível obter a fdp \(g(y)\) e a fda \(G(y)\). Inicialmente considere os gráficos de \(f(x)\) por \(x\) e \(y\) por \(x\). Pelos gráficos observa-se que

• \(f(x)=\frac{1}{2}, \; x \in [-1,1]\)
• \(y \in [1,3]\)

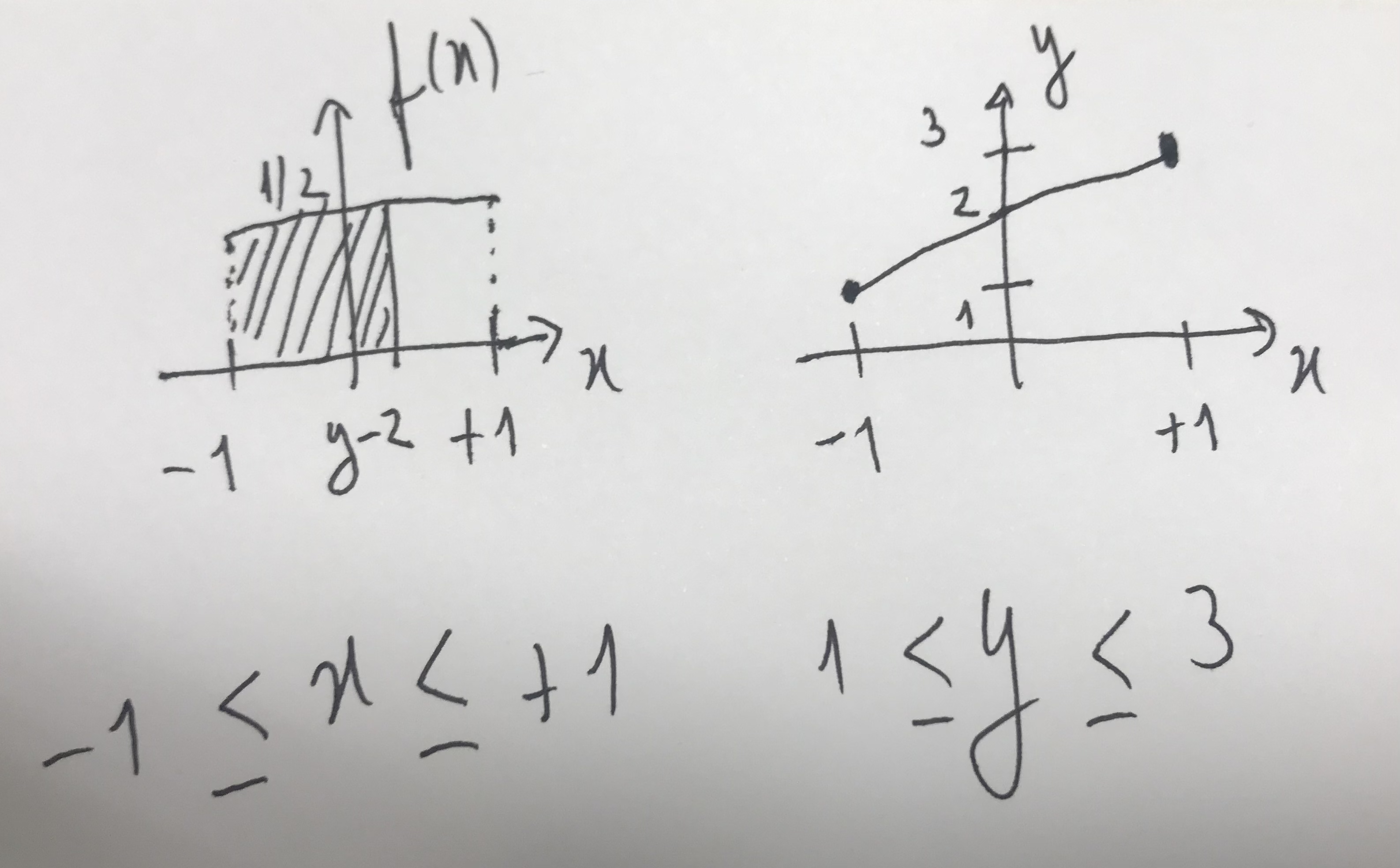
Passo 1

\[\begin{align*} G(y) &= P(Y \le y) \\ &= P(X+2 < y) \\ &= P(X < y-2) \\ &= \int_{-1}^{y-2} \frac{1}{2} dx \\ &= \frac{1}{2} [(y-2) - (-1)] \\ G(y) &= \frac{y-1}{2}, \; y \in [1,3] \end{align*}\]

Conferindo
\(G(1) = \frac{1-1}{2} = 0\)
\(G(3) = \frac{3-1}{2} = 1\)

Passo 2

\[\begin{align*} g(y) &= [G(y)]' \\ &= \left[\frac{1}{2} (y-1) \right]' \\ g(y) &= \frac{1}{2}, \; y \in [1,3] \end{align*}\]

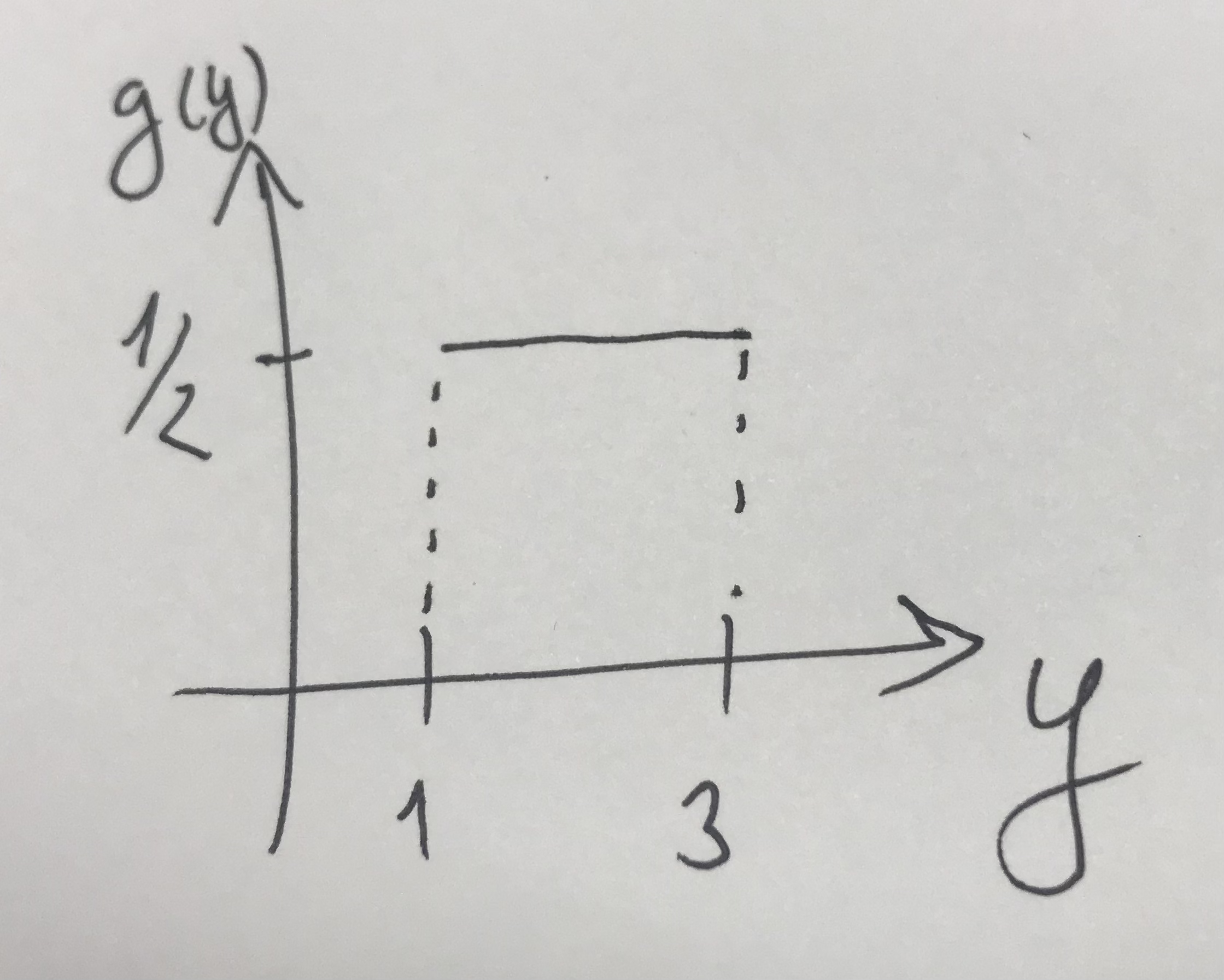
Logo, \(Y \sim \mathcal{U}[1,3]\).

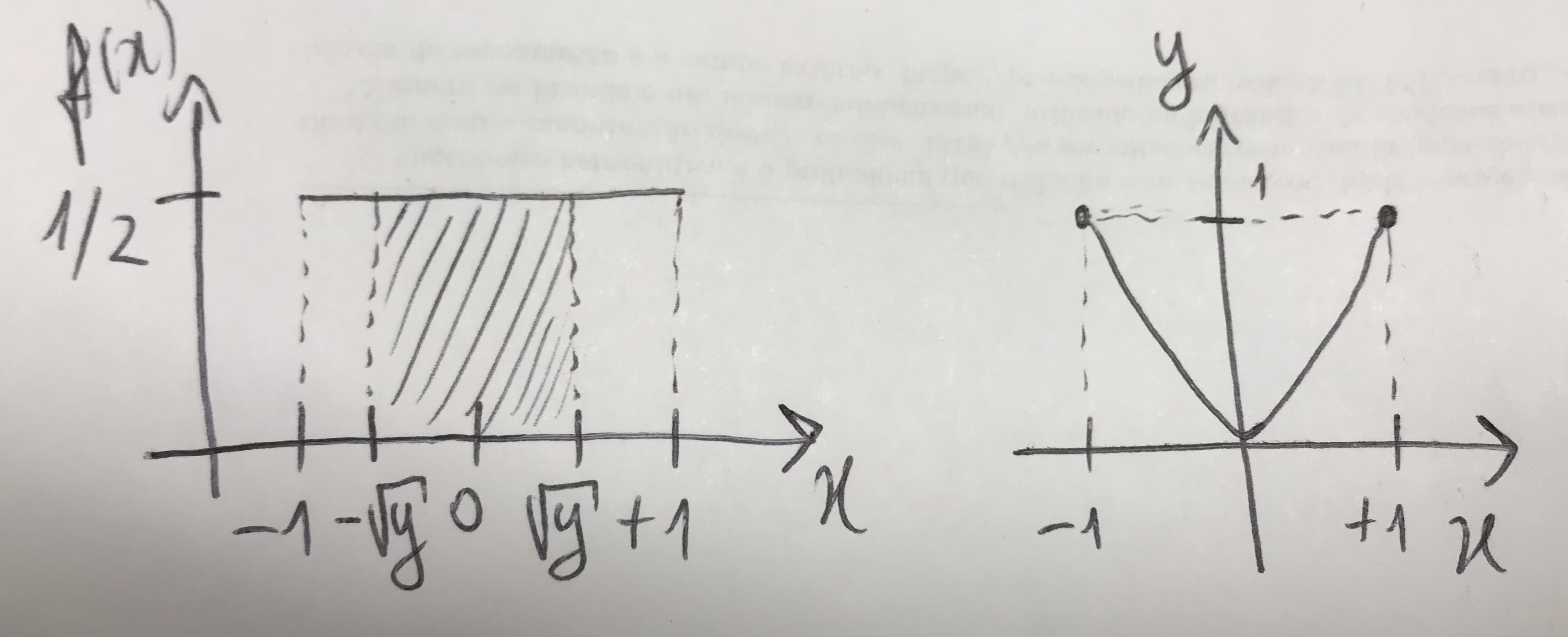
Exemplo 2.2 Seja a variável aleatória \(X \sim \mathcal{U}(-1,1)\) e a função \(Y=X^2\). É possível obter a fdp \(g(y)\). Inicialmente considere os gráficos de \(f(x)\) por \(x\) e \(y\) por \(x\). Pelos gráficos observa-se que

• \(f(x)=\frac{1}{2}, \; x \in [-1,1]\)
• \(y \in [0,1]\)

Passo 1

\[\begin{align*} G(y) &= P(Y \le y) \\ &= P(X^2 < y) \\ &= P(-\sqrt{y} < X < \sqrt{y}) \\ &= \int_{-\sqrt{y}}^{\sqrt{y}} \frac{1}{2} dx \\ &= \frac{1}{2} [\sqrt{y} - (-\sqrt{y})] \\ G(y) &= \sqrt{y}, \; y \in [0,1] \end{align*}\]

Conferindo
\(G(0) = \sqrt{0} = 0\)
\(G(1) = \sqrt{1} = 1\)

Passo 2

\[\begin{align*} g(y) &= [G(y)]' \\ &= \frac{1}{2} y^{\frac{1}{2}-1} \\ &= \frac{1}{2 \sqrt{y}}\\ g(y) &= \frac{\sqrt{y}}{2y}, \; y \in [0,1] \end{align*}\]

Conferindo
\(\int_{0}^{1} \frac{1}{2} y^{-\frac{1}{2}} dy = \frac{1}{2}[2y^{\frac{1}{2}}] \Big|_0^1 = 1\)

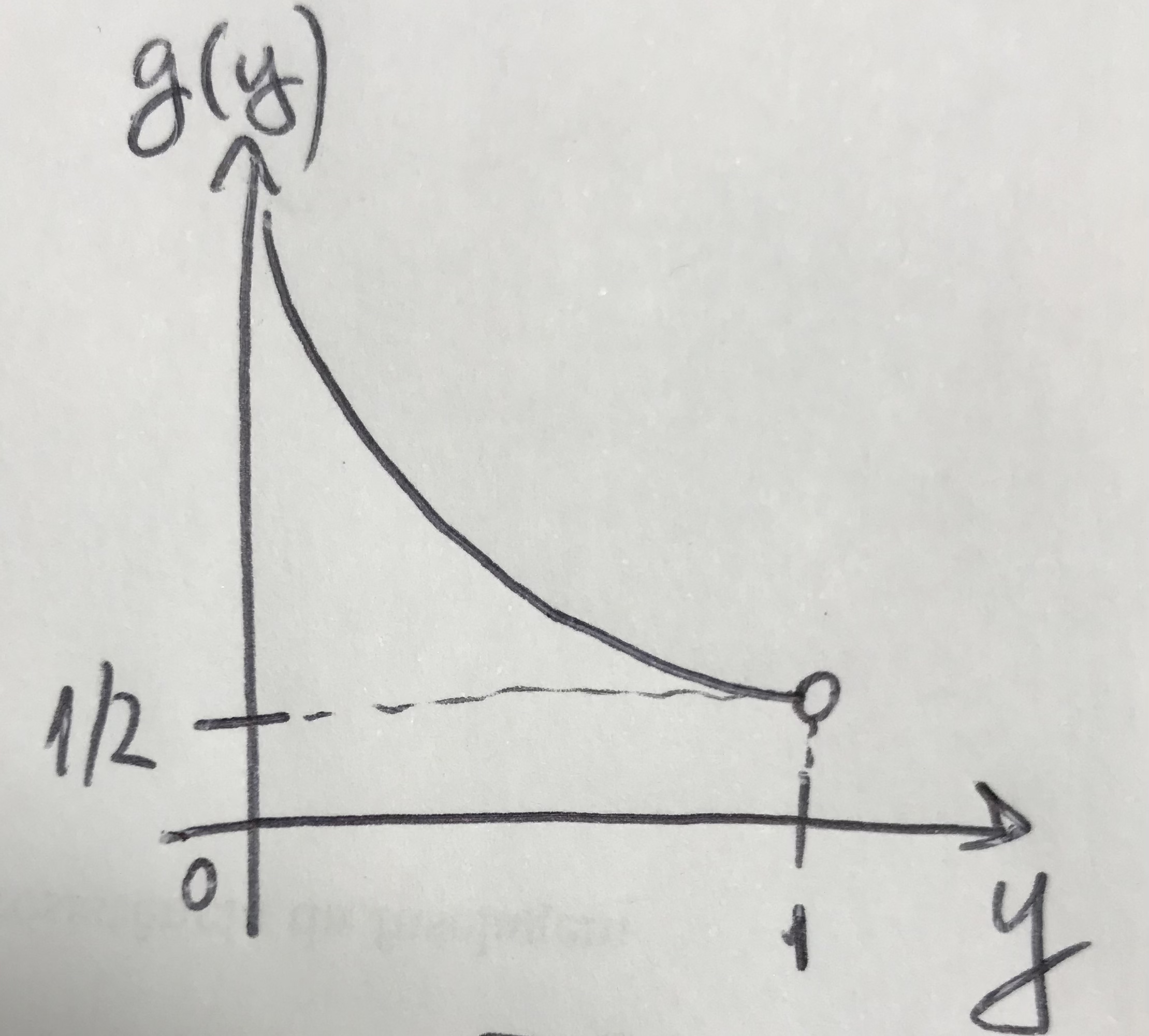
Finalmente é possível fazer o gráfico de \(g(y)\) por \(y\), verificando-se \(g(y) \in (1/2,\infty)\).

Exercício 2.1 Veja A bizarre probability fact do canal 3Blue1Brown. Obtenha as funções distribuição acumulada e densidade das variáveis aleatórias descritas no vídeo.