10.9 Árvores de Classificação e Regressão (CART)

(Breiman et al. 1984) apresentam o método de Árvores de Classificação e Regressão (Classification And Regression Trees). Consideram medidas¹⁴ (e.g. idade, pressão sanguínea, etc.) \(x_1,x_2,\ldots\) associadas a um caso e reunidas em um vetor de medida¹⁵ \(\boldsymbol{x}\). O espaço de medida¹⁶ \(\mathcal{X}\) contém todos os possíveis vetores de medida. Os casos ou objetos pertencem a \(J\) classes, sendo \(C\) o conjunto das classes tal que \(C=\{1,2,\ldots,J\}\). Desta forma, para todo \(\boldsymbol{x} \in \mathcal{X}\) um classificador ou regra de classificação atribui uma das classes \(\{1,2,\ldots,J\}\) a \(\boldsymbol{x}\).

Definição 10.1 Um classificador ou regra de classificação é uma função \(d(\boldsymbol{x})\) definida em \(\mathcal{X}\) de modo que para cada \(\boldsymbol{x}\), \(d(\boldsymbol{x})\) é igual a um dos números \(1,2,\ldots,J\). \(\\\)

Pode-se também definir \(A_j\) como o subconjunto de \(\mathcal{X}\) no qual \(d(\boldsymbol{x})=j\), i.e., \[A_j = \{ \boldsymbol{x}; d(\boldsymbol{x}) = j \}.\] Como \(\bigcap\limits_{j} A_j=\emptyset\) e \(\mathcal{X} = \bigcup\limits_{j} A_j\), os \(A_j\) formam uma partição de \(\mathcal{X}\) e pode-se definir de forma equivalente:

Definição 10.2 Um classificador é uma partição de \(\mathcal{X}\) em \(J\) subconjuntos disjuntos \(A_1,\ldots,A_j\), \(\mathcal{X} = \bigcup\limits_{j} A_j\) tais que para cada \(\boldsymbol{x} \in A_j\) a classe predita é \(J\). \(\\\)

(Breiman et al. 1984, 20–21) definem que classificadores estruturados (em árvore binária) ou (binary tree) structured classifiers na sigla em inglês. São construídos por repetidas divisões (splits) de subconjuntos de \(\mathcal{X}\) em dois subconjuntos descendentes, iniciando com o próprio \(\mathcal{X}\). A sugestão dos autores é indicar subconjuntos não terminais por círculos e terminais por uma caixa retangular, ainda que nenhuma implementação encontrada opere desta forma.

São indicados três elementos para a construção de uma árvore:

A seleção das divisões.
As decisões de quando declarar um nó terminal ou continuar a dividi-lo.
A atribuição de cada nó terminal a uma classe.

A ideia básica é selecionar cada divisão de um subconjunto de maneira que os dados em cada um dos subconjuntos descendentes sejam “mais puros” do que os dados do subconjunto pai. Os quatro elementos necessários no procedimento inicial de construção da árvore são:

Um conjunto \(Q\) de questões binárias da forma \(\{x \in A?\}\), \(A \subset \mathcal{X}\).
Um critério da qualidade da divisão \(\phi(s,t)\) que pode ser avaliado para qualquer divisão \(s\) de qualquer nó \(t\).
Uma regra para parar de dividir.
Uma regra para atribuir cada nó terminal a uma classe.

Definição 10.3 Uma função de impureza é uma função \(\phi\) definida no conjunto de todas as \(J\)-tuplas de números \((p_1,\ldots,p_J)\) satisfazendo \(p_j \ge 0\) (\(j=1,\ldots,J\) \(\sum_{j}) e p_j=1\) com as proriedades

\(\phi\) é um máximo apenas no ponto \(\left( \frac{1}{j},\frac{1}{j},\ldots,\frac{1}{j} \right)\)
\(\phi\) atinge seu mínimo apenas nos pontos \((1, 0, \ldots, 0)\), \((0,1,0, \ldots, 0)\), …, \((0,0, \ldots, 0,1)\),
\(\phi\) é uma função simétrica de \((p_1,\ldots,p_J)\)

Definição 10.4 Dada uma função de impureza \(\phi\), defini-se a medida de impureza \(i(t)\) de qualquer nó \(t\) como \[i(t) = \phi( p(1|t),p(2|t),\ldots,p(J|t) )\] Se uma divisão \(s\) de um nó \(t\) envia uma proporção \(p_R\) dos casos em \(t\) para \(t_R\) e a proporção \(p_L\) para \(t_L\), define-se a diminuição na impureza como \[\Delta i(s,t) = i(t) - p_R i(t_R) - p_L i(t_L)\]

10.9.1 `rpart`

O R base disponibiliza a função rpart::rpart (Therneau and Atkinson 2019), que realiza o particionamento recursivo e as árvores de regressão baseado em (Breiman et al. 1984). Detalhes da implementação podem ser encontrados aqui.

library(rpart)
fit <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis)
fit2 <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis,
              parms = list(prior = c(.65,.35), split = 'information'))
fit3 <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis,
              control = rpart.control(cp = 0.05))

# gráficos
# par(mfrow = c(1,3), xpd = NA) # caso contrário, em alguns dispositivos, o texto fica cortado
plot(fit)
text(fit, use.n = TRUE)

plot(fit2)
text(fit2, use.n = TRUE)

plot(fit3)
text(fit3, use.n = TRUE)

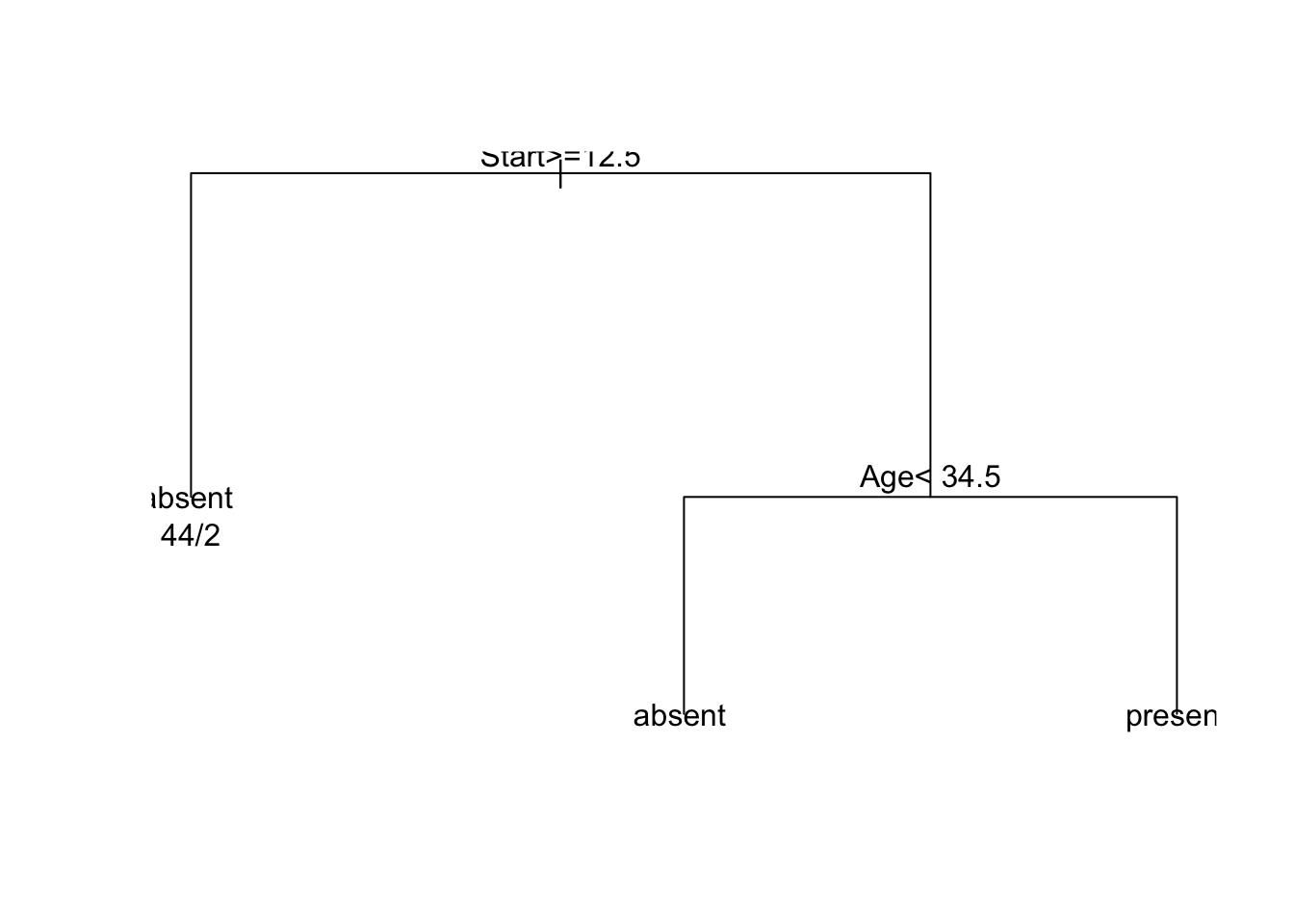
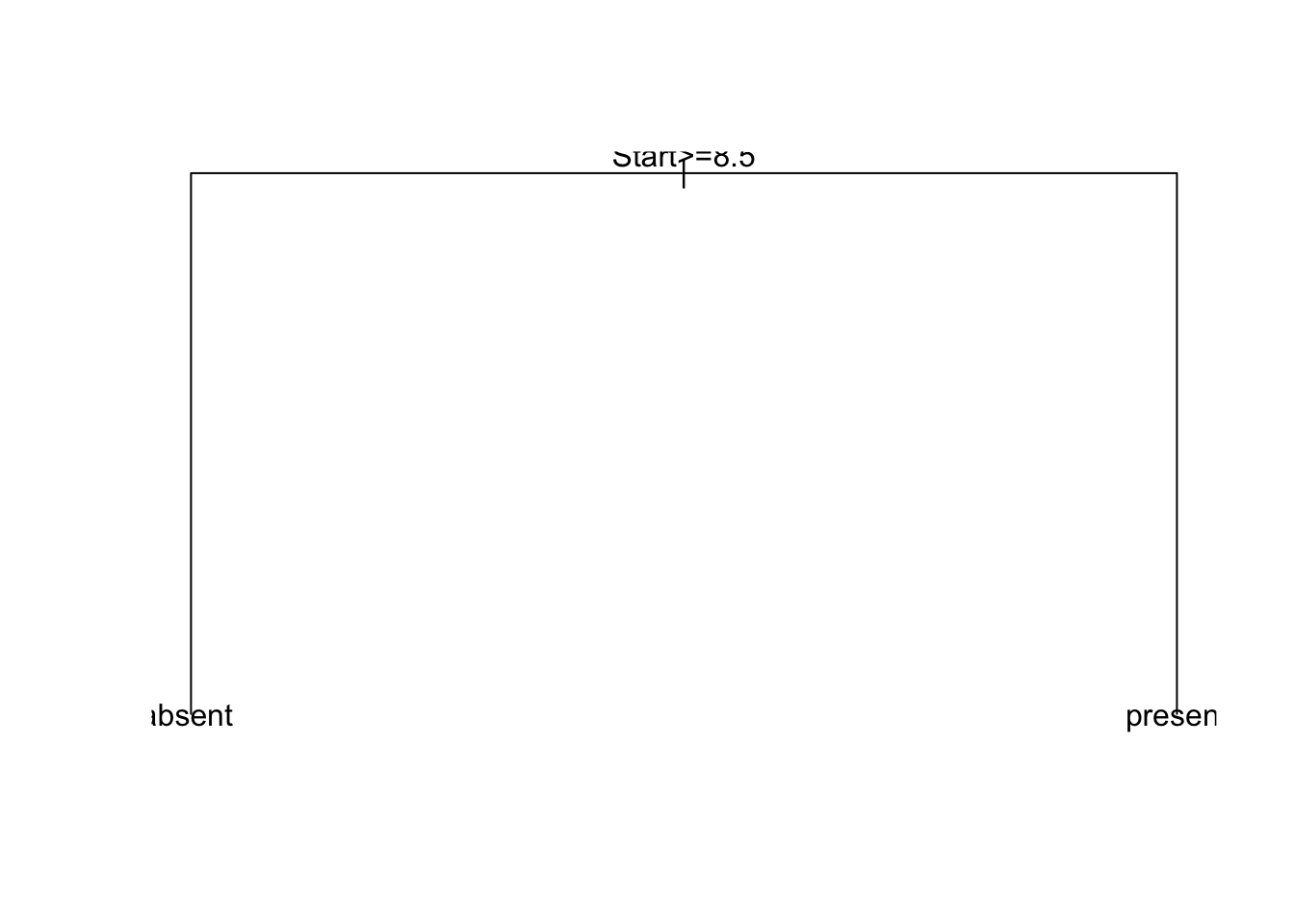
O pacote rpart.plot (Milborrow 2020) traz funções para apresentar árvores visualmente mais elegantes.

library(rpart.plot)
prp(fit)

prp(fit2)

prp(fit3)

rpart.plot(fit)

rpart.plot(fit2)

rpart.plot(fit3)

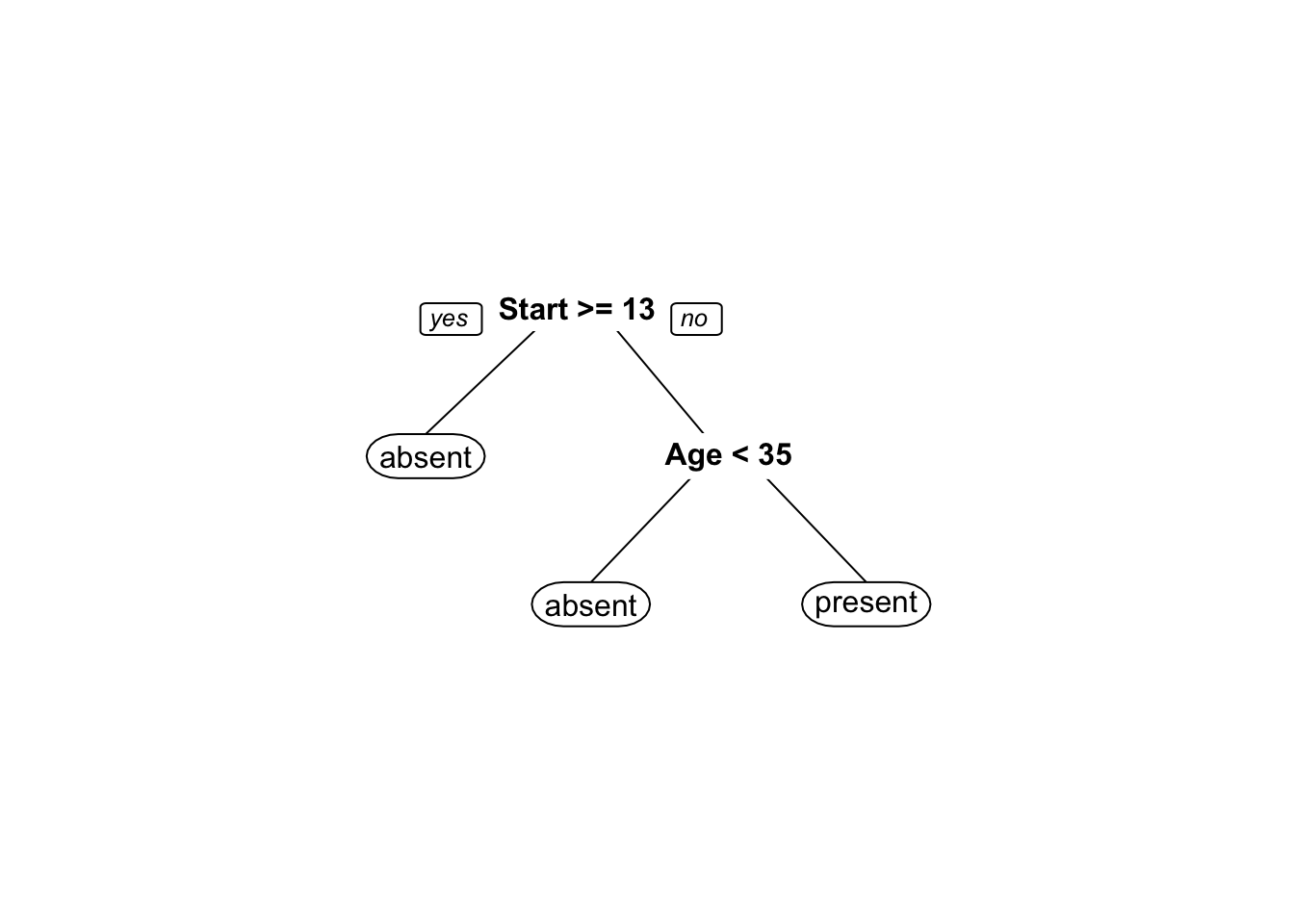
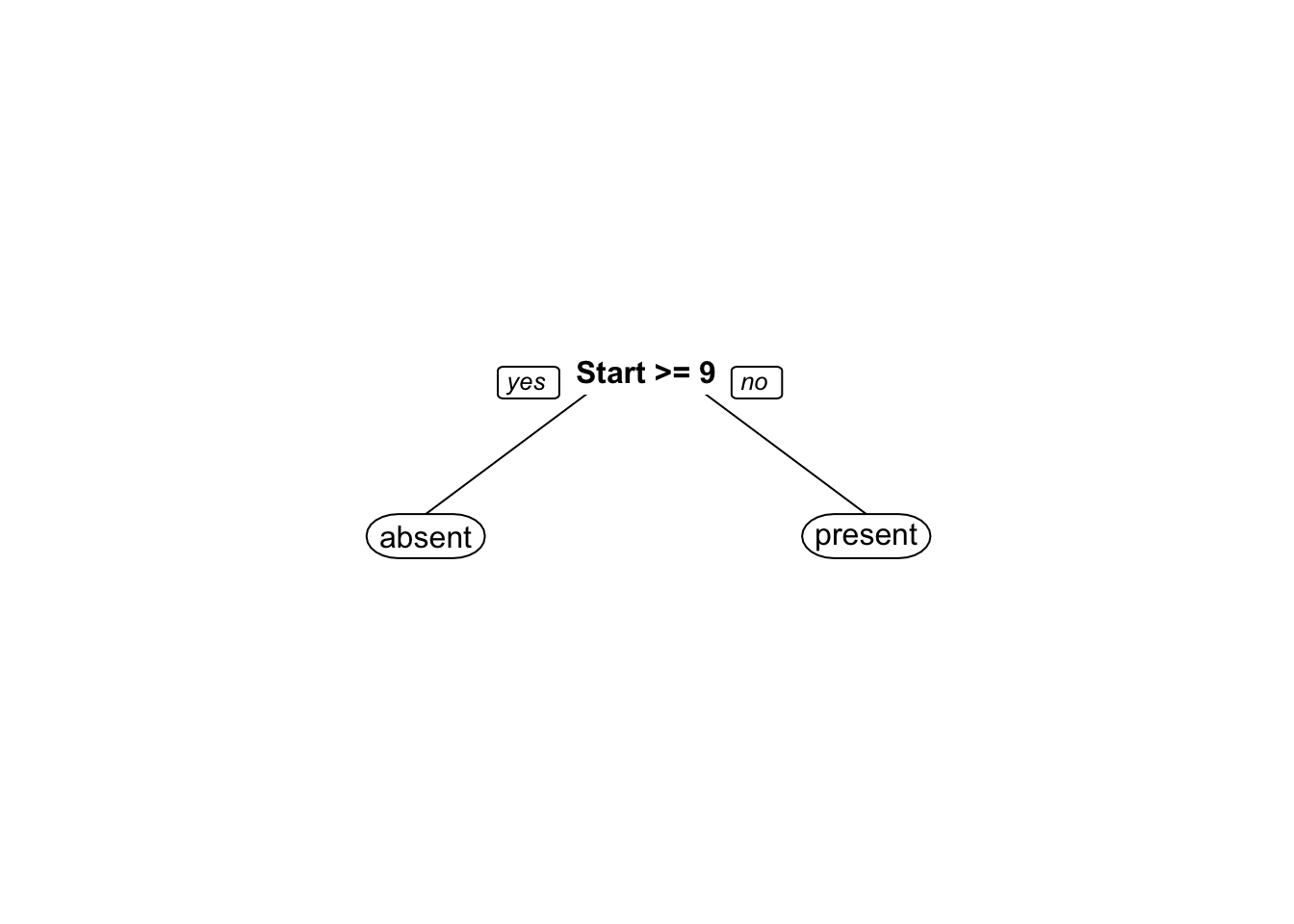
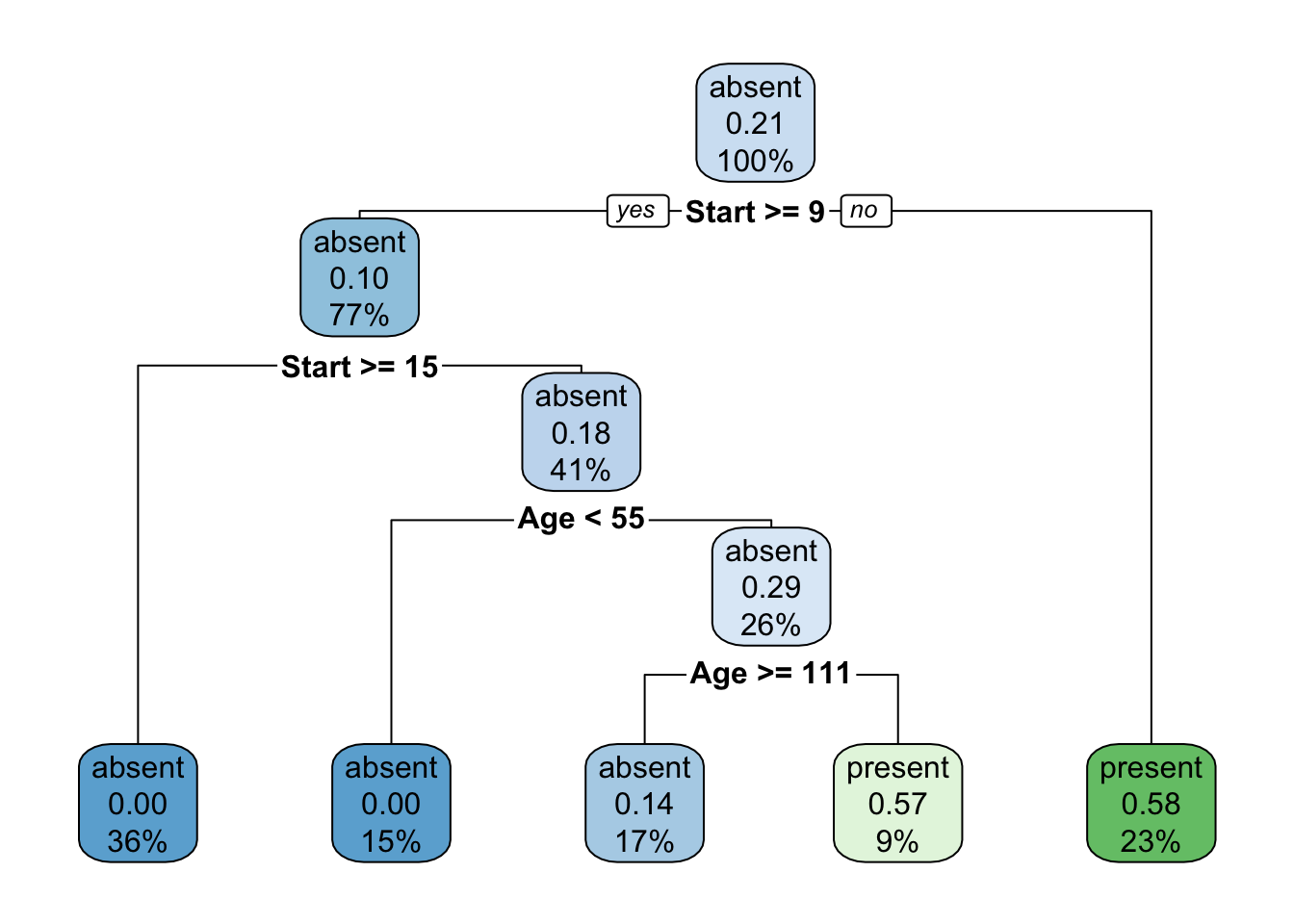
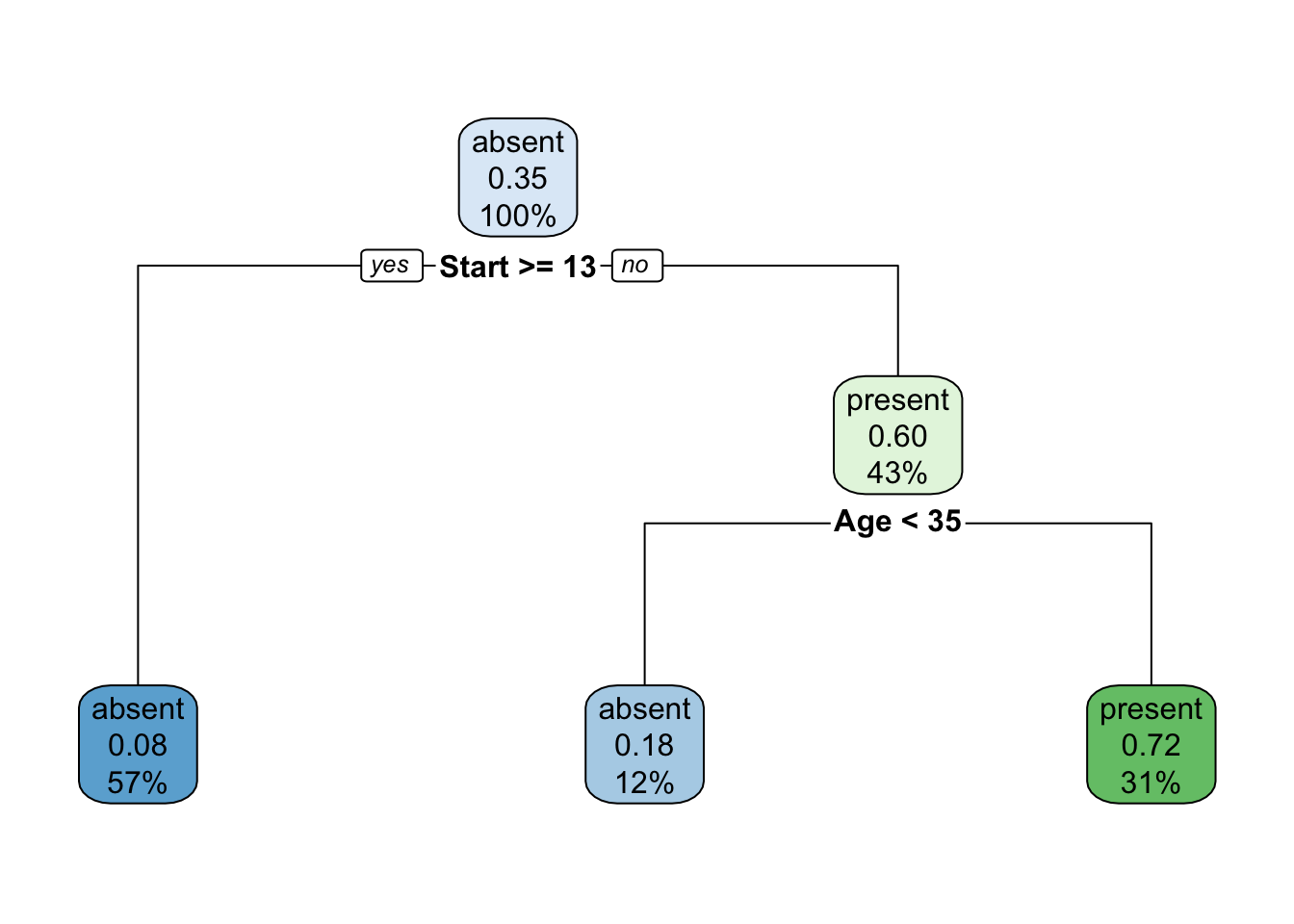
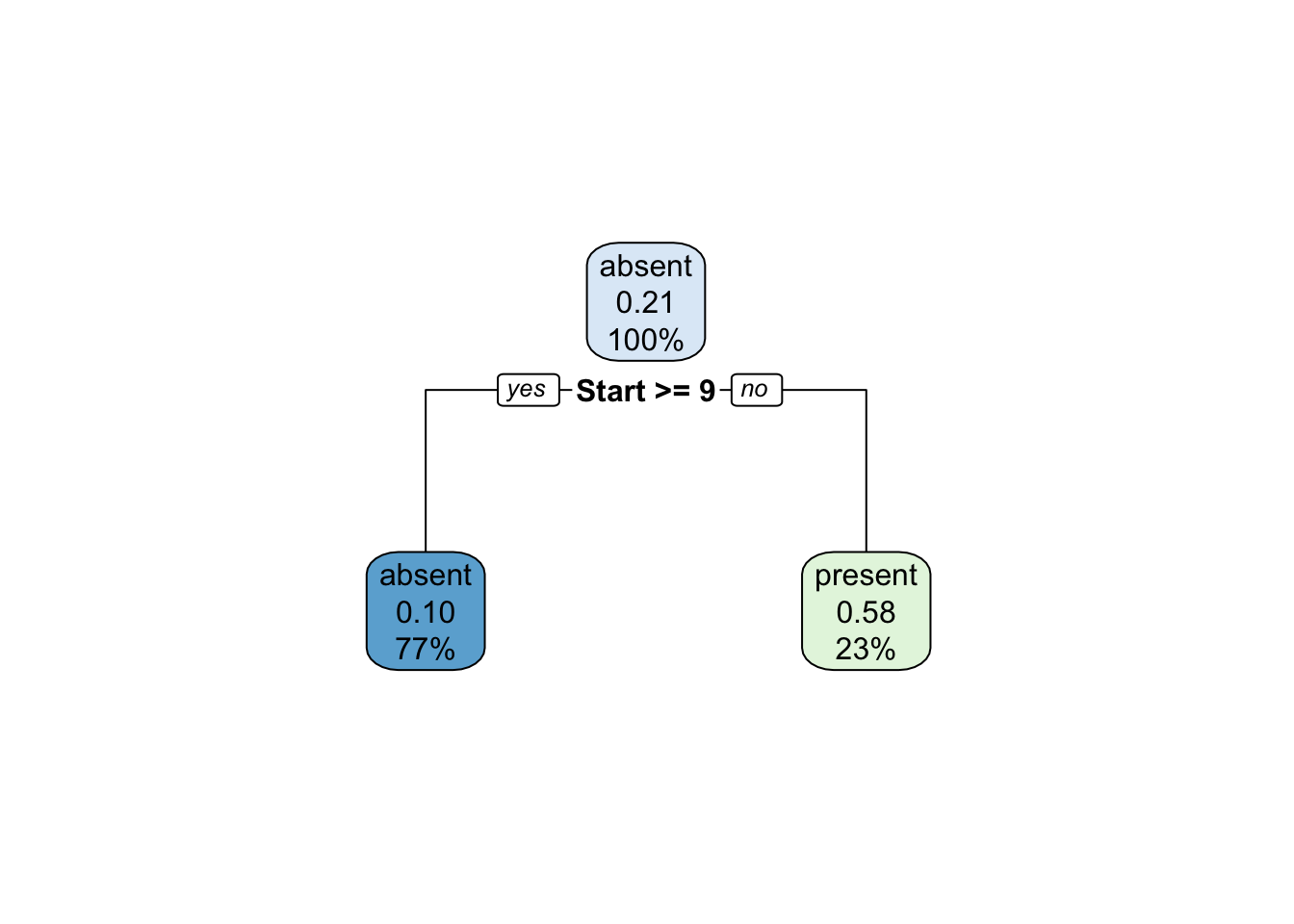
Exemplo 10.26 Classificando espécies de lírio via CART.

# amostra de treino: 60%
set.seed(1); itrain <- sort(sample(1:nrow(iris), floor(.6*nrow(iris))))
train <- iris[itrain,]
test <- iris[-itrain,]
# modelo
fit <- rpart::rpart(Species ~ ., data = train, method = 'class')
# plot
rpart.plot::rpart.plot(fit)

# predição
pred <- predict(fit, test, type = 'class')
# matriz de confusão
(cm <- table(pred, test[,5]))

##             
## pred         setosa versicolor virginica
##   setosa         18          0         0
##   versicolor      0         23         1
##   virginica       0          1        17

# relatório via caret::confusionMatrix
caret::confusionMatrix(cm)

## Confusion Matrix and Statistics
## 
##             
## pred         setosa versicolor virginica
##   setosa         18          0         0
##   versicolor      0         23         1
##   virginica       0          1        17
## 
## Overall Statistics
##                                           
##                Accuracy : 0.9667          
##                  95% CI : (0.8847, 0.9959)
##     No Information Rate : 0.4             
##     P-Value [Acc > NIR] : < 2.2e-16       
##                                           
##                   Kappa : 0.9495          
##                                           
##  Mcnemar's Test P-Value : NA              
## 
## Statistics by Class:
## 
##                      Class: setosa Class: versicolor Class: virginica
## Sensitivity                    1.0            0.9583           0.9444
## Specificity                    1.0            0.9722           0.9762
## Pos Pred Value                 1.0            0.9583           0.9444
## Neg Pred Value                 1.0            0.9722           0.9762
## Prevalence                     0.3            0.4000           0.3000
## Detection Rate                 0.3            0.3833           0.2833
## Detection Prevalence           0.3            0.4000           0.3000
## Balanced Accuracy              1.0            0.9653           0.9603

10.9.2 `tree`

(Ripley 2019) implementa mais ferramentas baseadas em (Breiman et al. 1984) e no Capítulo 7 de (Ripley 2007) (Tree-structured Classifiers).

library(tree)
ir.tr <- tree(Species ~., iris)
ir.tr

## node), split, n, deviance, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 150 329.600 setosa ( 0.33333 0.33333 0.33333 )  
##    2) Petal.Length < 2.45 50   0.000 setosa ( 1.00000 0.00000 0.00000 ) *
##    3) Petal.Length > 2.45 100 138.600 versicolor ( 0.00000 0.50000 0.50000 )  
##      6) Petal.Width < 1.75 54  33.320 versicolor ( 0.00000 0.90741 0.09259 )  
##       12) Petal.Length < 4.95 48   9.721 versicolor ( 0.00000 0.97917 0.02083 )  
##         24) Sepal.Length < 5.15 5   5.004 versicolor ( 0.00000 0.80000 0.20000 ) *
##         25) Sepal.Length > 5.15 43   0.000 versicolor ( 0.00000 1.00000 0.00000 ) *
##       13) Petal.Length > 4.95 6   7.638 virginica ( 0.00000 0.33333 0.66667 ) *
##      7) Petal.Width > 1.75 46   9.635 virginica ( 0.00000 0.02174 0.97826 )  
##       14) Petal.Length < 4.95 6   5.407 virginica ( 0.00000 0.16667 0.83333 ) *
##       15) Petal.Length > 4.95 40   0.000 virginica ( 0.00000 0.00000 1.00000 ) *

summary(ir.tr)

## 
## Classification tree:
## tree(formula = Species ~ ., data = iris)
## Variables actually used in tree construction:
## [1] "Petal.Length" "Petal.Width"  "Sepal.Length"
## Number of terminal nodes:  6 
## Residual mean deviance:  0.1253 = 18.05 / 144 
## Misclassification error rate: 0.02667 = 4 / 150

10.9.3 `data.tree`

(Glur 2020) apresenta ferramentas gerais para tratar dados com estrutura hierárquica. Uma boa introdução pode ser encontrada aqui ou pelo comando vignette(applications, package=data.tree).

library(data.tree)

vignette('applications', package = 'data.tree')

data(acme)
acme$Do(function(x) x$cost <- Aggregate(x, 'cost', sum))
Prune(acme, function(x) x$cost > 700000)

## [1] 5

print(acme, 'cost')

##                  levelName    cost
## 1 Acme Inc.                4950000
## 2  ¦--Accounting           1500000
## 3  ¦   °--New Software     1000000
## 4  °--Research             2750000
## 5      ¦--New Product Line 2000000
## 6      °--New Labs          750000

10.9.4 `RWeka`

(Hornik, Buchta, and Zeileis 2009) apresentam uma interface R para Weka de (Witten and Frank 2005). Weka é uma coleção de algoritmos de aprendizado de máquina para tarefas de mineração de dados escritos em Java, contendo ferramentas para pré-processamento, classificação, regressão, agrupamento, regras de associação e visualização de dados. Para obter mais informações sobre o Weka, consulte http://www.cs.waikato.ac.nz/ml/weka/.

# library(RWeka)
# m1 <- J48(Species ~ ., data = iris)
# writeLines(rJava::.jstrVal(m1$classifier))

(Breiman 1996c) discute heurísticas de instabilidade e estabilização na seleção de modelos.

10.9.5 C4.5 e C5.0

(Quinlan 1993) e (Kuhn and Quinlan 2021) apresentam modelos de árvores de decisão (decision trees) e baseados em regras (rule-based). Uma boa introdução pode ser encontrada aqui.

library(C50)
library(modeldata)
data(mlc_churn)

treeModel <- C50::C5.0(x = mlc_churn[1:3333, -20], y = mlc_churn$churn[1:3333])
treeModel

## 
## Call:
## C5.0.default(x = mlc_churn[1:3333, -20], y = mlc_churn$churn[1:3333])
## 
## Classification Tree
## Number of samples: 3333 
## Number of predictors: 19 
## 
## Tree size: 27 
## 
## Non-standard options: attempt to group attributes

summary(treeModel)

## 
## Call:
## C5.0.default(x = mlc_churn[1:3333, -20], y = mlc_churn$churn[1:3333])
## 
## 
## C5.0 [Release 2.07 GPL Edition]      Wed Apr 24 16:56:05 2024
## -------------------------------
## 
## Class specified by attribute `outcome'
## 
## Read 3333 cases (20 attributes) from undefined.data
## 
## Decision tree:
## 
## total_day_minutes > 264.4:
## :...voice_mail_plan = yes:
## :   :...international_plan = no: no (45/1)
## :   :   international_plan = yes: yes (8/3)
## :   voice_mail_plan = no:
## :   :...total_eve_minutes > 187.7:
## :       :...total_night_minutes > 126.9: yes (94/1)
## :       :   total_night_minutes <= 126.9:
## :       :   :...total_day_minutes <= 277: no (4)
## :       :       total_day_minutes > 277: yes (3)
## :       total_eve_minutes <= 187.7:
## :       :...total_eve_charge <= 12.26: no (15/1)
## :           total_eve_charge > 12.26:
## :           :...total_day_minutes <= 277:
## :               :...total_night_minutes <= 224.8: no (13)
## :               :   total_night_minutes > 224.8: yes (5/1)
## :               total_day_minutes > 277:
## :               :...total_night_minutes > 151.9: yes (18)
## :                   total_night_minutes <= 151.9:
## :                   :...account_length <= 123: no (4)
## :                       account_length > 123: yes (2)
## total_day_minutes <= 264.4:
## :...number_customer_service_calls > 3:
##     :...total_day_minutes <= 160.2:
##     :   :...total_eve_charge <= 19.83: yes (79/3)
##     :   :   total_eve_charge > 19.83:
##     :   :   :...total_day_minutes <= 120.5: yes (10)
##     :   :       total_day_minutes > 120.5: no (13/3)
##     :   total_day_minutes > 160.2:
##     :   :...total_eve_charge > 12.05: no (130/24)
##     :       total_eve_charge <= 12.05:
##     :       :...total_eve_calls <= 125: yes (16/2)
##     :           total_eve_calls > 125: no (3)
##     number_customer_service_calls <= 3:
##     :...international_plan = yes:
##         :...total_intl_calls <= 2: yes (51)
##         :   total_intl_calls > 2:
##         :   :...total_intl_minutes <= 13.1: no (173/7)
##         :       total_intl_minutes > 13.1: yes (43)
##         international_plan = no:
##         :...total_day_minutes <= 223.2: no (2221/60)
##             total_day_minutes > 223.2:
##             :...total_eve_charge <= 20.5: no (295/22)
##                 total_eve_charge > 20.5:
##                 :...voice_mail_plan = yes: no (20)
##                     voice_mail_plan = no:
##                     :...total_night_minutes > 174.2: yes (50/8)
##                         total_night_minutes <= 174.2:
##                         :...total_day_minutes <= 246.6: no (12)
##                             total_day_minutes > 246.6:
##                             :...total_day_charge <= 43.33: yes (4)
##                                 total_day_charge > 43.33: no (2)
## 
## 
## Evaluation on training data (3333 cases):
## 
##      Decision Tree   
##    ----------------  
##    Size      Errors  
## 
##      27  136( 4.1%)   <<
## 
## 
##     (a)   (b)    <-classified as
##    ----  ----
##     365   118    (a): class yes
##      18  2832    (b): class no
## 
## 
##  Attribute usage:
## 
##  100.00% total_day_minutes
##   93.67% number_customer_service_calls
##   87.73% international_plan
##   20.73% total_eve_charge
##    8.97% voice_mail_plan
##    8.01% total_intl_calls
##    6.48% total_intl_minutes
##    6.33% total_night_minutes
##    4.74% total_eve_minutes
##    0.57% total_eve_calls
##    0.18% account_length
##    0.18% total_day_charge
## 
## 
## Time: 0.0 secs

plot(treeModel)

Exercício 10.9 Melhorar a visualização do gráfico gerado por plot(treeModel).

Exemplo 10.27 Classificando espécies de lírio via C5.0.

# amostra de treino: 60%
set.seed(1); itrain <- sort(sample(1:nrow(iris), floor(.6*nrow(iris))))
train <- iris[itrain,]
test <- iris[-itrain,]
# modelo
fit <- C50::C5.0(x = train[,-5], y = as.factor(train[,5]))
summary(fit)

## 
## Call:
## C5.0.default(x = train[, -5], y = as.factor(train[, 5]))
## 
## 
## C5.0 [Release 2.07 GPL Edition]      Wed Apr 24 16:56:06 2024
## -------------------------------
## 
## Class specified by attribute `outcome'
## 
## Read 90 cases (5 attributes) from undefined.data
## 
## Decision tree:
## 
## Petal.Length <= 1.9: setosa (32)
## Petal.Length > 1.9:
## :...Petal.Width > 1.7: virginica (28)
##     Petal.Width <= 1.7:
##     :...Petal.Length <= 4.9: versicolor (24)
##         Petal.Length > 4.9:
##         :...Petal.Width <= 1.5: virginica (3)
##             Petal.Width > 1.5: versicolor (3/1)
## 
## 
## Evaluation on training data (90 cases):
## 
##      Decision Tree   
##    ----------------  
##    Size      Errors  
## 
##       5    1( 1.1%)   <<
## 
## 
##     (a)   (b)   (c)    <-classified as
##    ----  ----  ----
##      32                (a): class setosa
##            26          (b): class versicolor
##             1    31    (c): class virginica
## 
## 
##  Attribute usage:
## 
##  100.00% Petal.Length
##   64.44% Petal.Width
## 
## 
## Time: 0.0 secs

# plot
plot(fit)

# predição
pred <- predict(fit, test)
# matriz de confusão
(cm <- table(pred, test[,5]))

##             
## pred         setosa versicolor virginica
##   setosa         18          0         0
##   versicolor      0         23         1
##   virginica       0          1        17

# relatório via caret::confusionMatrix
caret::confusionMatrix(cm)

## Confusion Matrix and Statistics
## 
##             
## pred         setosa versicolor virginica
##   setosa         18          0         0
##   versicolor      0         23         1
##   virginica       0          1        17
## 
## Overall Statistics
##                                           
##                Accuracy : 0.9667          
##                  95% CI : (0.8847, 0.9959)
##     No Information Rate : 0.4             
##     P-Value [Acc > NIR] : < 2.2e-16       
##                                           
##                   Kappa : 0.9495          
##                                           
##  Mcnemar's Test P-Value : NA              
## 
## Statistics by Class:
## 
##                      Class: setosa Class: versicolor Class: virginica
## Sensitivity                    1.0            0.9583           0.9444
## Specificity                    1.0            0.9722           0.9762
## Pos Pred Value                 1.0            0.9583           0.9444
## Neg Pred Value                 1.0            0.9722           0.9762
## Prevalence                     0.3            0.4000           0.3000
## Detection Rate                 0.3            0.3833           0.2833
## Detection Prevalence           0.3            0.4000           0.3000
## Balanced Accuracy              1.0            0.9653           0.9603

Referências

———. 1996c. “Heuristics of Instability and Stabilization in Model Selection.” The Annals of Statistics 24 (6): 2350–83. https://www.jstor.org/stable/2242688.

Breiman, Leo, Jerome Friedman, Charles J Stone, and Richard A Olshen. 1984. Classification and Regression Trees. CRC press.

Glur, Christoph. 2020. Data.tree: General Purpose Hierarchical Data Structure. https://CRAN.R-project.org/package=data.tree.

Hornik, Kurt, Christian Buchta, and Achim Zeileis. 2009. “Open-Source Machine Learning: R Meets Weka.” Computational Statistics 24 (2): 225–32. https://doi.org/10.1007/s00180-008-0119-7.

Kuhn, Max, and Ross Quinlan. 2021. C50: C5.0 Decision Trees and Rule-Based Models. https://CRAN.R-project.org/package=C50.

Milborrow, Stephen. 2020. Rpart.plot: Plot ’Rpart’ Models: An Enhanced Version of ’Plot.rpart’. https://CRAN.R-project.org/package=rpart.plot.

Quinlan, J. Ross. 1993. C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers, Inc., San Mateo, CA. https://books.google.com.br/books/about/C4_5.html?id=HExncpjbYroC.

Ripley, Brian D. 2007. Pattern Recognition and Neural Networks. Cambridge University Press.

———. 2019. Tree: Classification and Regression Trees. https://CRAN.R-project.org/package=tree.

Therneau, Terry, and Beth Atkinson. 2019. Rpart: Recursive Partitioning and Regression Trees. https://CRAN.R-project.org/package=rpart.

Witten, Ian H., and Eibe Frank. 2005. Data Mining: Practical Machine Learning Tools and Techniques. 2nd ed. San Francisco: Morgan Kaufmann.

Measurements.↩︎
Measurement vector.↩︎
Measurement space.↩︎