9.7 Regressão logística
9.7.1 Variáveis binárias/dicotômicas
Em problemas aplicados é comum fazer uso de variáveis aleatórias que admitam apenas dois valores, chamadas v.a. binárias ou dicotômicas. Empresas de serviços financeiros podem estar interessados em clientes adimplentes/inadimpletes, hospitais em pacientes com/sem melhora, cientistas da computação em servidores operantes/inoperantes, etc. Começamos com um exemplo numérico para ilustrar.
Exemplo 9.17 Um banco está interessado na variável aleatória \(Y\): cliente inadimplente. Ela assume valor 1 se o
cliente é inadimplente (sucesso) e 0 caso contrário (fracasso). Note que a terminologia sucesso/fracasso indica se a variável \(Y\) foi observada (1) ou não (0), ainda que ‘sucesso’ possa não significar algo agradável.
Se considerarmos 40 clientes, 20 inadimplentes e 20 adimplentes, pode-se calcular a probabilidade (incondicional) de observar um cliente inadimplente (sucesso) por \(Pr(Y=1)=\frac{20}{40}=0.5\). Da mesma forma, a probabilidade (incondicional) de observar um ciente adimplente (fracasso) é dada por \(Pr(Y=0)=\frac{20}{40}=0.5\). Utilizando a linguagem R pode-se gerar a sequência de zeros e uns descrita acima, bem como as respectivas probabilidades.
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1## y
## 0 1
## 20 20## y
## 0 1
## 0.5 0.5Vendo a questão desta maneira pode-se considerar que a probabilidade de um cliente ser inadimplente é de 50%. É possível, porém, considerar outras variáveis para refinar esta probabilidade. Suponha uma variável \(X_1\), que ocorre em aproximadamente 20% dos clientes adimplentes (\(Y=0\)) e em aproximadamente 90% dos clientes inadimplentes (\(Y=1\)). Assim, visto que presença da variável \(X_1\) é maior entre os inadimplentes, intuitivamente devemos atribuir uma probabilidade maior de inadimplência a clientes que apresentem a característica \(X_1\), e menor para aquele onde a característica \(X_1\) é ausente. Novamente podemos fazer uso da linguagem R para gerar sequências similares àquelas consideradas na teoria.
library(tidyverse)
set.seed(1); (x1 <- c(rbinom(n,1,.2), rbinom(n,1,.9))) # gerando sequência pseudoaleatória## [1] 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1Note na saída abaixo que o segmento indicado por \(\texttt{\$}\)’\(\texttt{0}\)’ refere-se ao grupo onde \(X_1=0\), e \(\texttt{\$}\)’\(\texttt{1}\)’ onde \(X_1=1\).
by(y,x1,table) %>% # contando o número de zeros e uns em y separado por x1
lapply(prop.table) # calculando as proporções ## $`0`
##
## 0 1
## 0.94117647 0.05882353
##
## $`1`
##
## 0 1
## 0.173913 0.826087Note que a probabilidade de inadimplência no grupo onde \(X_1\) não é observada é igual a \(Pr(Y=1|X_1=0) = 0.05882353\). No grupo de clientes que apresentam a característica \(X_1\) esta probabilidade sobe para \(Pr(Y=1|X_1=1) = 0.826087\).
Finalmente é considerada uma variável \(X_2\), que aparece em aproximadamente metade dos clientes inadimplentes e em aproximadamente metade dos adimplentes. Assim, observar a característica \(X_2\) não deve trazer informação sobre a probabilidade de inadimplência, simbolizada pela probabilidade condicional \(Pr(Y=1|X_2 = x_2)\), \(x_2 \in \{0,1\}\).
## [1] 0 0 1 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 0 0 1 0 0 1 0 0 1 1 1 0 1 0by(y,x2,table) %>% # contando os zeros e uns de y, separados pelos valores de X2
lapply(prop.table) # transformando a contagem em proporção## $`0`
##
## 0 1
## 0.4285714 0.5714286
##
## $`1`
##
## 0 1
## 0.5789474 0.42105269.7.2 Regressão logística binomial
A regressão logística binomial pertence à classe dos modelos lineares generalizados, descrita em detalhes por (McCullagh and Nelder 1989), (Agresti 2002) e (Paula 2013). Uma descrição sobre as origens da função logística é feita por (Cramer 2002).
9.7.2.1 Ligação logito
Uma das vantagens de usar ligações canônicas é que as mesmas garantem a concavidade de \(L(\beta)\) e consequentemente muitos resultados assintóticos são obtidos mais facilmente. Por exemplo, a concavidade de \(L(\beta)\) garante a unicidade da estimativa de máxima verossimilhança de \(\beta\), quando essa existe. (Paula 2013, 8).
Seja \(Y\) uma variável aleatória binária com distribuição binimial de probablidade de sucesso \(\pi(x)\). A notação \(\pi(x)\) sugere que a probabilidade de sucesso está condicionada a um valor/categoria \(x\). Desta forma, \(\pi(x) = Pr(Y=1|X=x)\). Define-se a função (canônica) logito conforme a Eq. (9.28), onde \(\mathrm{log}\) indica o logaritmo na base \(e \approx 2.71828\,18284\,59045\).
\[\begin{equation} \mathrm{logito}\left[ \pi(x) \right] = \mathrm{log} \left( \dfrac{\pi(x)}{1-\pi(x)} \right) = \beta_0 + \beta_1 x \tag{9.28} \end{equation}\]
Isolando \(\pi(x)\) na Eq. (9.28) obtém-se
\[\begin{equation} \pi(x) = \dfrac{e^{\beta_0 + \beta_1 x}}{1+e^{\beta_0 + \beta_1 x}} \tag{9.29} \end{equation}\]
Exemplo 9.18 Considerando novamente as informações do Exemplo 9.17, vamos agora utilizar a estrutura das Equações (9.28) e (9.29) para abordar o problema.
# modelo 1
x1 <- as.factor(x1) # convertendo em fator para usar a função glm
fit1 <- glm(y ~ x1, family = binomial(link = 'logit')) # ajustando modelo logístico, padrão
summary(fit1) # detalhamento do modelo##
## Call:
## glm(formula = y ~ x1, family = binomial(link = "logit"))
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.773 1.031 -2.690 0.00715 **
## x11 4.331 1.168 3.707 0.00021 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 55.452 on 39 degrees of freedom
## Residual deviance: 28.860 on 38 degrees of freedom
## AIC: 32.86
##
## Number of Fisher Scoring iterations: 5Note que o intercepto \(\hat{\beta}_0 = -2.773\) é significativo (\(p-value = 0.00715\)), bem como o coeficiente que indica a presença do atributo \(X_1\), \(\hat{\beta}_1 = 4.331\) (\(p-value = 0.00021\)). Assim, pode-se considerar o modelo conforme Eq. (9.28), na forma \[\mathrm{log} \left( \dfrac{\pi(x)}{1-\pi(x)} \right) = -2.773 + 4.331 I_{x_1}.\] A simbologia \(I_{x_1}\) representa uma variável indicadora da presença do atributo \(X_1\). Assim, se a pessoa possuir o atributo \(X_1\) considera-se \(I_{x_1}=1\), e \(I_{x_1}=0\) caso contrário. Este é um modelo conhecido como casela de referência, visto que a variável \(X_1\) é categórica. Desta forma, uma das categorias/níveis da variável é escolhida como a (casela de) referência. Por padrão, o R utiliza a primeira da ordem numérica/alfabética, no caso \(X_1=0\). Desta forma, se a pessoa não possui a característica \(X_1\), pode-se calcular sua probabilidade de inadimplência pela Eq. (9.29), dada por \[Pr(Y=1|X_1=0) = \pi(0) = \dfrac{e^{-2.773 + 4.331 \times 0}}{1+e^{-2.773 + 4.331 \times 0}} \approx 0.05882353.\] No caso de alguém que possui a característica \(X_1\), \[Pr(Y=1|X_1=1) = \pi(1) = \dfrac{e^{-2.773 + 4.331 \times 1}}{1+e^{-2.773 + 4.331 \times 1}} \approx 0.826087.\]
## (Intercept)
## 0.05882353## [1] 0.826087O mesmo procedimento considerado para \(X_1\) pode ser realizado para \(X_2\). Note que o intercepto \(\hat{\beta}_0 = 0.2877\) é não significativo (\(p-value = 0.514\)), bem como o coeficiente que indica a presença do atributo \(X_2\), \(\hat{\beta}_1 = -0.6061\) (\(p-value = 0.344\)).
# modelo 2
x2 <- as.factor(x2) # convertendo em fator para usar a função glm
fit2 <- glm(y ~ x2, family = 'binomial') # ajustando modelo logístico, padrão
summary(fit2) # detalhamento do modelo##
## Call:
## glm(formula = y ~ x2, family = "binomial")
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.2877 0.4410 0.652 0.514
## x21 -0.6061 0.6406 -0.946 0.344
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 55.452 on 39 degrees of freedom
## Residual deviance: 54.546 on 38 degrees of freedom
## AIC: 58.546
##
## Number of Fisher Scoring iterations: 4Desta maneira o modelo não deve ser utilizado, mas para efeito de comparação com os resultados do Exemplo 9.17 são calculadas as probabilidades de sucesso condicionadas a \(X_2=0\) e \(X_2=1\).
## (Intercept)
## 0.5714286## [1] 0.4210526Exercício 9.7 Considere o conjunto de dados apresentado por (Kohavi 1996), disponível em https://archive.ics.uci.edu/ml/datasets/adult. Um modelo de regressão logística foi utilizado para avaliar as características que mais impactam no salario das pessoas (acima ou abaixo de 50 mil dólares).
# lendo e arrumando os dados
url0 <- 'https://filipezabala.com/data/adult.data'
dat <- read.table(url0, sep = ',')
dat <- dat[,-c(3,9)]
colnames(dat) <- c('idade','tipoTrabalho','educacao','anosEstudo','estadoCivil',
'ocupacao','relacao','sexo','ganhoCapital','perdaCapital',
'horasPorSemana','paisOrigem','salario')
tab <- table(dat$salario)
dat$salario_bin <- vector(length = nrow(dat))
dat$salario_bin[dat$salario == names(tab)[1]] <- 0
dat$salario_bin[dat$salario == names(tab)[2]] <- 1
table(dat$salario_bin)##
## 0 1
## 24720 78419.7.2.2 Ligação probito
Veja (Paula 2013, 8–9).
\[\begin{equation} \Phi^{-1}\left[ \pi(x) \right] = \beta_0 + \beta_1 x \tag{9.30} \end{equation}\]
##
## Call:
## glm(formula = y ~ x1, family = binomial(link = "probit"))
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.5647 0.4866 -3.216 0.0013 **
## x11 2.5035 0.5757 4.348 1.37e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 55.452 on 39 degrees of freedom
## Residual deviance: 28.860 on 38 degrees of freedom
## AIC: 32.86
##
## Number of Fisher Scoring iterations: 59.7.2.3 Ligação complemento log-log
Veja (Paula 2013, 9–10).
\[\begin{equation} \log \left[ -\log (1-\pi(x)) \right] = \beta_0 + \beta_1 x \tag{9.31} \end{equation}\]
##
## Call:
## glm(formula = y ~ x1, family = binomial(link = "cloglog"))
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.8031 0.9999 -2.803 0.00506 **
## x11 3.3622 1.0331 3.254 0.00114 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 55.452 on 39 degrees of freedom
## Residual deviance: 28.860 on 38 degrees of freedom
## AIC: 32.86
##
## Number of Fisher Scoring iterations: 59.7.3 Regressão logística multinomial
Assim como a regressão logística binomial, a regressão logística multinomial pertence à classe dos modelos lineares generalizados. Considerando a abordagem de (Agresti 2002), seja \(Y\) uma variável aleatória categórica com \(J\) categorias. Seja \(\pi_j(\boldsymbol{x}) = Pr(Y=j|\boldsymbol{x})\), com \(\sum_{j} \pi_j(\boldsymbol{x}) = 1\). O modelo compara cada categoria \(j\) com uma categoria de referência \(J\), totalizando \({J \choose 2}\) combinações.
\[\begin{equation} \mathrm{log} \left( \frac{\pi_j(\boldsymbol{x})}{\pi_J(\boldsymbol{x})} \right) = \alpha_j + \boldsymbol{\beta}_j' \boldsymbol{x} \tag{9.32} \end{equation}\]
Isolando \(\pi_j(\boldsymbol{x})\) na Eq. (9.32) obtém-se
\[\begin{equation} \pi_j(\boldsymbol{x}) = \frac{e^{\alpha_j + \boldsymbol{\beta}_j' \boldsymbol{x}}}{1+e^{\alpha_j + \boldsymbol{\beta}_j' \boldsymbol{x}}} \tag{9.33} \end{equation}\]
Exemplo 9.19 Classificando espécies de lírio via regressão logística multinomial.
# amostra de treino: 60%
set.seed(1); itrain <- sort(sample(1:nrow(iris), floor(.6*nrow(iris))))
train <- iris[itrain,]
test <- iris[-itrain,]
# modelo
fit <- nnet::multinom(Species ~ ., data = train)## # weights: 18 (10 variable)
## initial value 98.875106
## iter 10 value 13.996830
## iter 20 value 4.540873
## iter 30 value 4.442713
## iter 40 value 4.427409
## iter 50 value 4.383847
## iter 60 value 4.374970
## iter 70 value 4.350357
## iter 80 value 4.349414
## iter 90 value 4.349189
## iter 100 value 4.349171
## final value 4.349171
## stopped after 100 iterations## Call:
## nnet::multinom(formula = Species ~ ., data = train)
##
## Coefficients:
## (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
## versicolor 16.68789 -9.87539 -4.584648 17.36299 -0.2303277
## virginica -29.57178 -10.24568 -10.961247 25.88805 14.3209004
##
## Std. Errors:
## (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
## versicolor 21.55566 16.83778 9.158921 11.07209 5.851094
## virginica 21.76088 16.74477 9.316057 10.87593 5.680874
##
## Residual Deviance: 8.698341
## AIC: 28.69834##
## pred setosa versicolor virginica
## setosa 18 0 0
## versicolor 0 24 2
## virginica 0 0 16## Confusion Matrix and Statistics
##
##
## pred setosa versicolor virginica
## setosa 18 0 0
## versicolor 0 24 2
## virginica 0 0 16
##
## Overall Statistics
##
## Accuracy : 0.9667
## 95% CI : (0.8847, 0.9959)
## No Information Rate : 0.4
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9492
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: setosa Class: versicolor Class: virginica
## Sensitivity 1.0 1.0000 0.8889
## Specificity 1.0 0.9444 1.0000
## Pos Pred Value 1.0 0.9231 1.0000
## Neg Pred Value 1.0 1.0000 0.9545
## Prevalence 0.3 0.4000 0.3000
## Detection Rate 0.3 0.4000 0.2667
## Detection Prevalence 0.3 0.4333 0.2667
## Balanced Accuracy 1.0 0.9722 0.9444## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
## Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500par(mfrow = c(1,2))
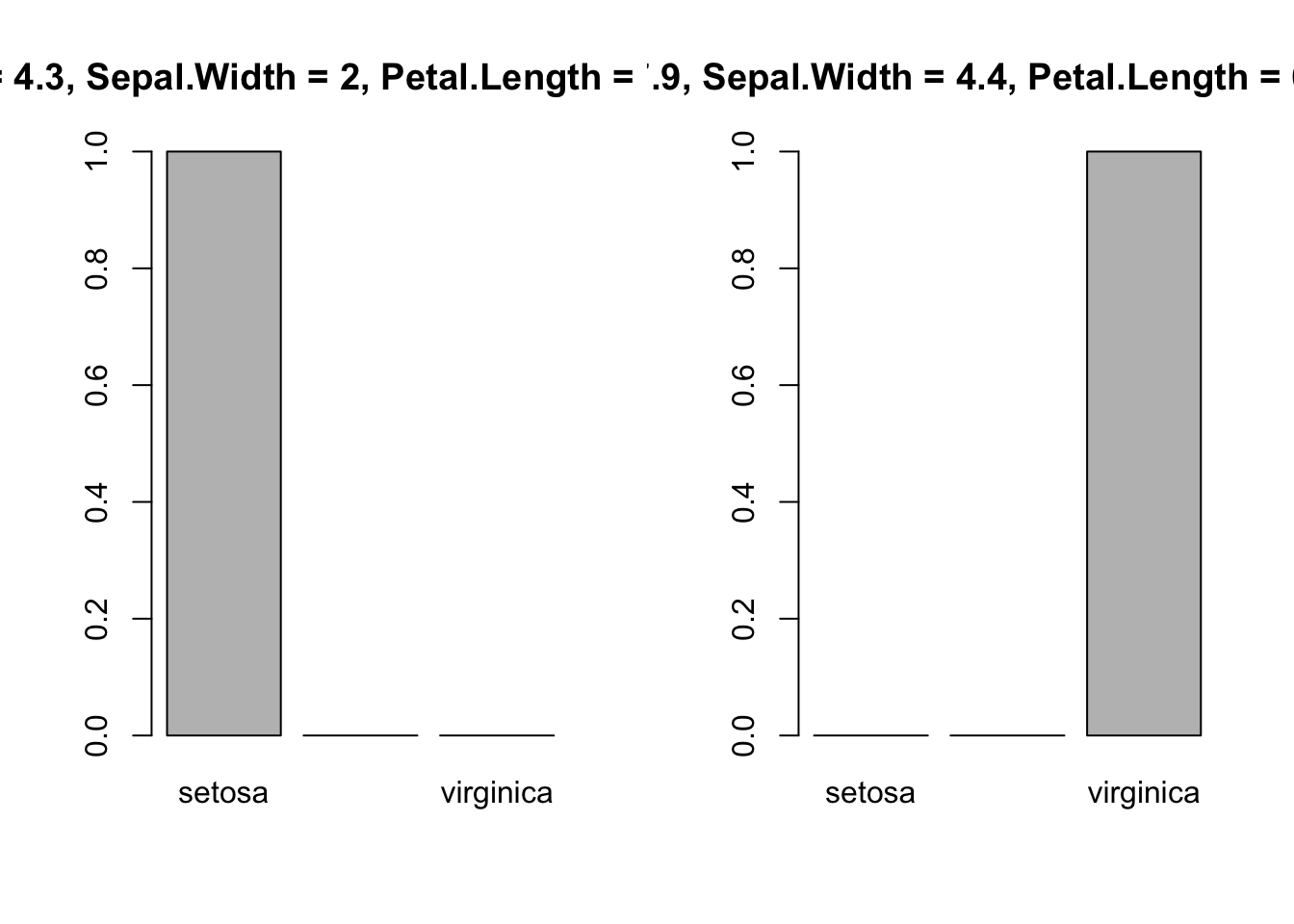
nd.1 <- data.frame(Sepal.Length = 4.3, Sepal.Width = 2, Petal.Length = 1, Petal.Width = 0.1)
pr.1 <- predict(fit, type = 'probs', newdata = nd.1)
barplot(pr.1, ylim = c(0,1))
title('Sepal.Length = 4.3, Sepal.Width = 2, Petal.Length = 1, Petal.Width = 0.1')
nd.2 <- data.frame(Sepal.Length = 7.9, Sepal.Width = 4.4, Petal.Length = 6.9, Petal.Width = 2.5)
pr.2 <- predict(fit, type = 'probs', newdata = nd.2)
barplot(pr.2, ylim = c(0,1))
title('Sepal.Length = 7.9, Sepal.Width = 4.4, Petal.Length = 6.9, Petal.Width = 2.5')