10.4 Exercícios
Exercício 10.7 Leia:
(a) a documentação da função fviz_nbclust.
(b) https://www.datanovia.com/en/lessons/determining-the-optimal-number-of-clusters-3-must-know-methods.
(c) A Seção e. Graphical Output Concerning Each Clustering, pg. 83-88 de (Rousseeuw and Kaufman 1990).
\(\\\)
Exercício 10.8 Considere novamente o conjunto de dados pib.
(a) Verifique as sugestões do número ótimo de grupos com os diferente métodos disponíveis na função fviz_nbclust.
(b) Crie o grupamento que considerar mais adequado aos dados e apresente com a função fviz_cluster.
(c) Compare os resultados com o Exercício 10.2.
\(\\\)
Exercício 10.9 Considere o conjunto de dados drinks, discutido no Capítulo ??.
(a) Calcule as distâncias de Manhattan, euclidiana e de Minkowski com \(p=3\).
(b) Obtenha os modelos hierárquicos utilizando as três distâncias do item (a). Você nota alguma diferença?
(c) Obtenha a seleção inicial dos centróides a partir de proposta de (Hartigan 1975) apresentada na Equação (10.7). Sugestão: escreva uma função que dependa dos dados e de \(k\), realizando alguma correção que considerar relevante.
(d) Calcule os centróides dos grupos obtidos no item (c).
(e) Calcule a \(VQI\) dos grupos obtidos no item (c) a partir da Eq. (10.5).
(f) Calcule a \(SQT\) dos grupos obtidos no item (c) a partir da Eq. (10.6).
(g) Verifique as sugestões do número ótimo de grupos com os diferente métodos disponíveis na função fviz_nbclust.
(h) Crie o grupamento que considerar mais adequado aos dados e apresente com a função fviz_cluster.
Exercício 10.10 Considere o banco de dados sobre eficiência energética didcutido no Exemplo 5.2.
(a) Calcule as distâncias de Manhattan, euclidiana e de Minkowski com \(p=3\).
(b) Obtenha os modelos hierárquicos utilizando as três distâncias do item (a). (PODE DEMORAR!)
(c) Verifique as sugestões do número ótimo de grupos com os diferente métodos disponíveis na função fviz_nbclust.
(d) Crie o grupamento que considerar mais adequado aos dados e apresente com a função fviz_cluster.
library(readxl)
url1 <- 'http://archive.ics.uci.edu/ml/machine-learning-databases/00242/ENB2012_data.xlsx'
download.file(url1, 'temp.xlsx', mode = 'wb')
dat <- read_excel('temp.xlsx')10.4.1 Fuzzy C-Means
Bezdek (1974; 1981)
Bezdek, Ehrlich and Full (1984) - FCM—the Fuzzy C-Means clustering-algorithm
10.4.4 Apriori
https://en.wikipedia.org/wiki/Apriori_algorithm https://www.geeksforgeeks.org/apriori-algorithm-in-r-programming/ https://dl.acm.org/doi/pdf/10.1145/170035.170072 https://rsrikant.com/papers/thesis.pdf https://arxiv.org/pdf/1403.3948 https://borgelt.net/papers/cstat_02.pdf
# Loading Libraries
library(arules)
library(arulesViz)
library(RColorBrewer)
# import dataset
data("Groceries")
# using apriori() function
rules <- apriori(Groceries,
parameter = list(supp = 0.01, conf = 0.2))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen maxlen target ext
## 0.2 0.1 1 none FALSE TRUE 5 0.01 1 10 rules TRUE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 98
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
## sorting and recoding items ... [88 item(s)] done [0.00s].
## creating transaction tree ... done [0.00s].
## checking subsets of size 1 2 3 4 done [0.00s].
## writing ... [232 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].## lhs rhs support confidence coverage lift count
## [1] {} => {whole milk} 0.25551601 0.2555160 1.00000000 1.000000 2513
## [2] {hard cheese} => {whole milk} 0.01006609 0.4107884 0.02450432 1.607682 99
## [3] {butter milk} => {other vegetables} 0.01037112 0.3709091 0.02796136 1.916916 102
## [4] {butter milk} => {whole milk} 0.01159126 0.4145455 0.02796136 1.622385 114
## [5] {ham} => {whole milk} 0.01148958 0.4414062 0.02602949 1.727509 113
## [6] {sliced cheese} => {whole milk} 0.01077783 0.4398340 0.02450432 1.721356 106
## [7] {oil} => {whole milk} 0.01128622 0.4021739 0.02806304 1.573968 111
## [8] {onions} => {other vegetables} 0.01423488 0.4590164 0.03101169 2.372268 140
## [9] {onions} => {whole milk} 0.01209964 0.3901639 0.03101169 1.526965 119
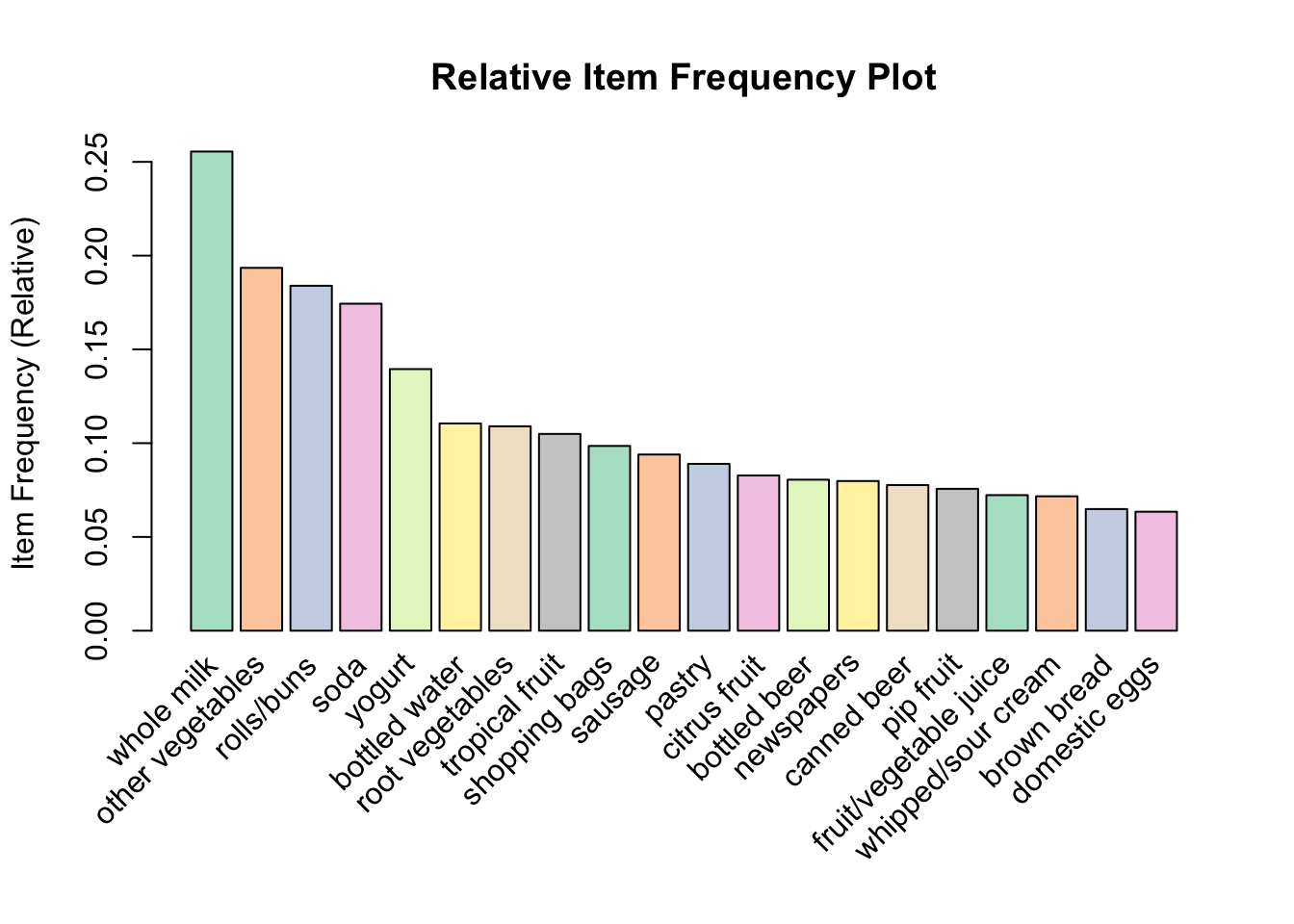
## [10] {berries} => {yogurt} 0.01057448 0.3180428 0.03324860 2.279848 104# using itemFrequencyPlot() function
arules::itemFrequencyPlot(Groceries, topN = 20,
col = brewer.pal(8, 'Pastel2'),
main = 'Relative Item Frequency Plot',
type = "relative",
ylab = "Item Frequency (Relative)")