10.2 Métodos hierárquicos
Como o nome sugere, os métodos hierárquicos buscam uma estrutura hierárquica dos grupos. Esta estrutura geralmente se dá em forma de árvore, onde os objetos são apresentados individualmente como um grupo unitário (folha/leaf) que se aglomeram por similaridade em grupos maiores (nós/nodes) ligados por um grande grupo que une todos elementos (raiz/root). Os passos para realizar um agrupamento hierárquico aglomerativo estão descritos a seguir.
ALGORITMO DE AGRUPAMENTO HIERÁRQUICO AGLOMERATIVO
PASSO 1 Padronizar os dados, geralmente com o uso da função
scale.
PASSO 2 Calcular a (dis)similaridade entre cada par de objetos no conjunto de dados.
PASSO 3 Usar a função de ligação para agrupar os objetos na árvore a partir das informações de distância obtidas na passo 1.
PASSO 4 Criar uma partição dos dados via gráfico da árvore hierárquica em grupos (dendrograma), ou cutree .
Exemplo 10.4 O conjunto de dados USArrests contém estatísticas sobre detenções por 100,000 residentes por agressão, homicídio e violação em cada um dos 50 estados dos EUA em 1973. Também é fornecida a percentagem da população que vive em áreas urbanas. Veja (Census 1975) e (McNeil 1977).
# 1. padronizando os dados
USArrest.scale <- scale(USArrests)
# 2. calculando distâncias (utilizando o padrão: euclidean)
dUSA <- stats::dist(USArrest.scale)
# 3. aplicando a função de ligação (utilizando o padrão: complete)
hc <- hclust(dUSA)
# 4. apresentando o gráfico
plot(hc)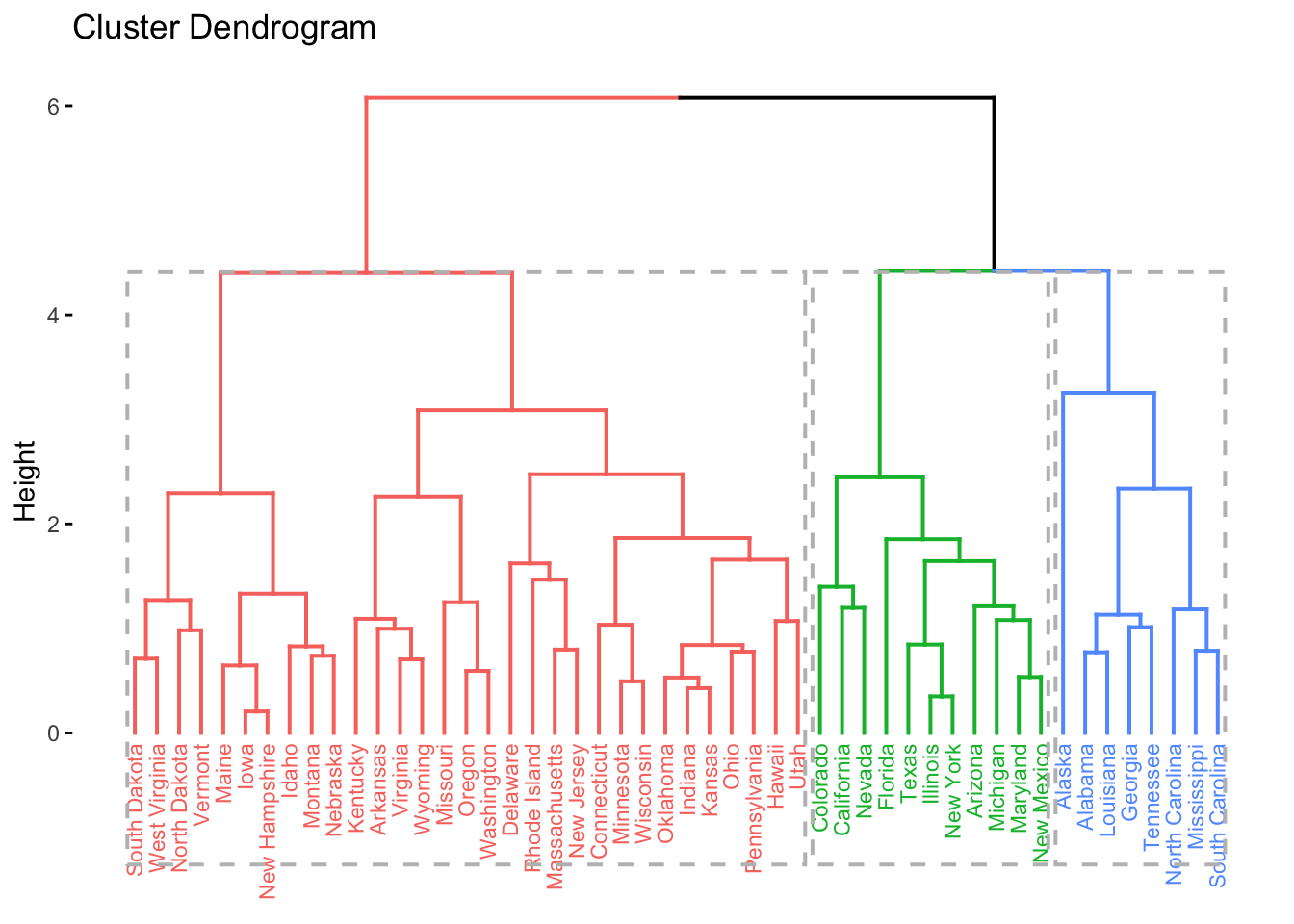
10.2.1 Ligação entre Agrupamentos
Segundo a documentação, a função stats::hclust “realiza uma análise hierárquica de cluster usando um conjunto de diferenças para os \(n\) objetos que estão sendo agrupados. Inicialmente, cada objeto é atribuído ao seu próprio cluster e então o algoritmo prossegue iterativamente, em cada estágio unindo os dois clusters mais semelhantes, continuando até que haja apenas um único cluster. Em cada estágio, as distâncias entre os clusters são recalculadas pela fórmula de atualização de dissimilaridade de Lance-Williams de acordo com o método de agrupamento específico que está sendo usado.
Vários métodos de cluster diferentes são fornecidos. O método de variância mínima de Ward visa encontrar aglomerados esféricos compactos. O método de ligação completa encontra clusters semelhantes. O método de ligação única (que está intimamente relacionado à árvore geradora mínima) adota uma estratégia de agrupamento de “amigos de amigos”. Os outros métodos podem ser considerados como visando clusters com características em algum lugar entre os métodos de link único e completo. Observe, no entanto, que os métodos “mediana” e “centróide” não levam a uma medida de distância monótona ou, equivalentemente, os dendrogramas resultantes podem ter as chamadas inversões ou reversões que são difíceis de interpretar, mas observe as tricotomias em (Legendre and Legendre 2012).
Dois algoritmos diferentes são encontrados na literatura para agrupamento de Ward. A opção “ward.D” não implementa o critério de agrupamento de (Ward Jr 1963), enquanto a opção “ward.D2” implementa esse critério (Murtagh and Legendre 2014). Com este último, as diferenças são elevadas ao quadrado antes da atualização do cluster.
Nas exibições hierárquicas de cluster, é necessária uma decisão em cada fusão para especificar qual subárvore deve ficar à esquerda e qual deve ficar à direita. Como, para n observações, há
\(n−1\) mesclagens, existem \(2^{n-1}\) ordenações possíveis para as folhas em uma árvore de cluster, ou dendrograma. O algoritmo usado em hclust é ordenar a subárvore de modo que o cluster mais compacto fique à esquerda (a última mesclagem, ou seja, a mais recente, da subárvore esquerda tem um valor inferior ao da última mesclagem da subárvore direita). As observações únicas são os agrupamentos mais compactos possíveis, e as fusões envolvendo duas observações as colocam em ordem pelo seu número de sequência de observação.
10.2.1.1 Distâncias cofenéticas
Any classification or partition can be fully described by a cophenetic matrix. This matrix is used for comparing different classifications of the same objects. (Legendre and Legendre 2012, 312)
Os valores no eixo \(y\), intitulados height, são as chamadas distâncias cofenéticas propostas por (Sokal and Rohlf 1962). O nome vem da área da Biologia chamada fenética, que estuda métodos de classificação por similaridade fenotípica. Seu cálculo não é complexo, mas pode ser trabalhoso; assim, será considerada a função stats::cophenetic para a obtenção de tais distâncias. Quanto maior for seu valor, mais dissimilar são os elementos comparados. Correlação elevada entre as distâncias calculadas e as distâncias cofenéticas sugere um bom agrupamento.
## [1] 0.2058539 0.3502188 0.4287712 0.4940832 0.5303259 0.5303259 0.5353893 0.5935343 0.6457158 0.6457158
## [11] 0.7038309 0.7108812 0.7389936 0.7722224 0.7781298 0.7865674 0.7977642 0.8286936 0.8286936 0.8412900
## [21] 0.8412900 0.8412900 0.8412900 0.8412900 0.8412900 0.8457697 0.8457697 0.9824857 0.9971035 0.9971035
## [31] 1.0122252 1.0354597 1.0354597 1.0709720 1.0800988 1.0800988 1.0918624 1.0918624 1.0918624 1.1314351
## [41] 1.1314351 1.1314351 1.1314351 1.1826891 1.1826891 1.1968261 1.2117356 1.2117356 1.2117356 1.2502752
## [51] 1.2502752 1.2716808 1.2716808 1.2716808 1.2716808 1.3329504 1.3329504 1.3329504 1.3329504 1.3329504
## [61] 1.3329504 1.3329504 1.3329504 1.3329504 1.3988595 1.3988595 1.4668378 1.4668378 1.6230495 1.6230495
## [71] 1.6230495 1.6448574 1.6448574 1.6448574 1.6448574 1.6448574 1.6448574 1.6448574 1.6448574 1.6448574
## [81] 1.6448574 1.6448574 1.6448574 1.6585736 1.6585736 1.6585736 1.6585736 1.6585736 1.6585736 1.6585736
## [91] 1.6585736 1.6585736 1.6585736 1.8537984 1.8537984 1.8537984 1.8537984 1.8537984 1.8537984 1.8537984
## [101] 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801
## [111] 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801 1.8649801
## [121] 1.8649801 2.2630242 2.2630242 2.2630242 2.2630242 2.2630242 2.2630242 2.2630242 2.2630242 2.2630242
## [131] 2.2630242 2.2630242 2.2630242 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287
## [141] 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287
## [151] 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.2952287 2.3374653 2.3374653 2.3374653
## [161] 2.3374653 2.3374653 2.3374653 2.3374653 2.3374653 2.3374653 2.3374653 2.3374653 2.3374653 2.4458600
## [171] 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600
## [181] 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600 2.4458600
## [191] 2.4458600 2.4458600 2.4458600 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807
## [201] 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807
## [211] 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807
## [221] 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807 2.4748807
## [231] 2.4748807 2.4748807 2.4748807 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [241] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [251] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [261] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [271] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [281] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [291] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [301] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [311] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [321] 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430 3.0883430
## [331] 3.0883430 3.2554326 3.2554326 3.2554326 3.2554326 3.2554326 3.2554326 3.2554326 4.4005416 4.4005416
## [341] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [351] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [361] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [371] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [381] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [391] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [401] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [411] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [421] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [431] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [441] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [451] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [461] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [471] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [481] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [491] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [501] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [511] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [521] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [531] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416
## [541] 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4005416 4.4200736 4.4200736
## [551] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [561] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [571] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [581] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [591] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [601] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [611] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [621] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736
## [631] 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 4.4200736 6.0766416 6.0766416 6.0766416 6.0766416
## [641] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [651] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [661] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [671] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [681] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [691] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [701] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [711] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [721] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [731] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [741] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [751] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [761] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [771] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [781] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [791] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [801] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [811] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [821] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [831] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [841] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [851] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [861] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [871] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [881] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [891] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [901] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [911] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [921] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [931] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [941] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [951] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [961] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [971] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [981] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [991] 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416 6.0766416
## [ reached 'max' / getOption("max.print") -- omitted 225 entries ]# Correlação entre as distâncias cofenéticas e as distâncias originais (maior, melhor)
cor(coph,dUSA)## [1] 0.697943710.2.2 Biblioteca factoextra
É possível melhorar a visualização do dendrograma utilizando a função factoextra::fviz_dend.
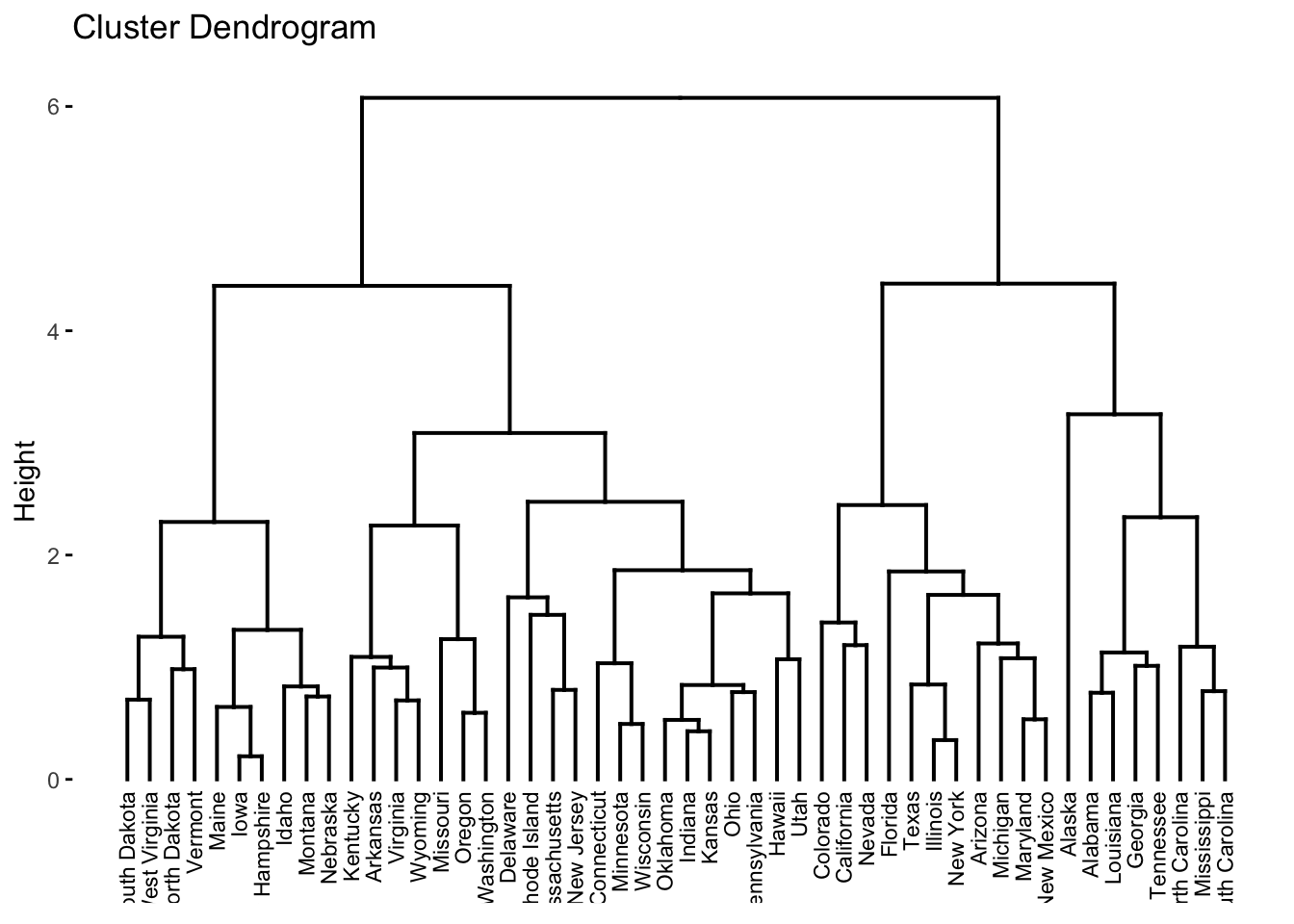
Pode-se utilizar a função fviz_dend para colorir um número arbitrário de grupos. Note que os grupamentos são obtidos de cima pra baixo, dependente dos valores de height (distâncias cofenéticas).
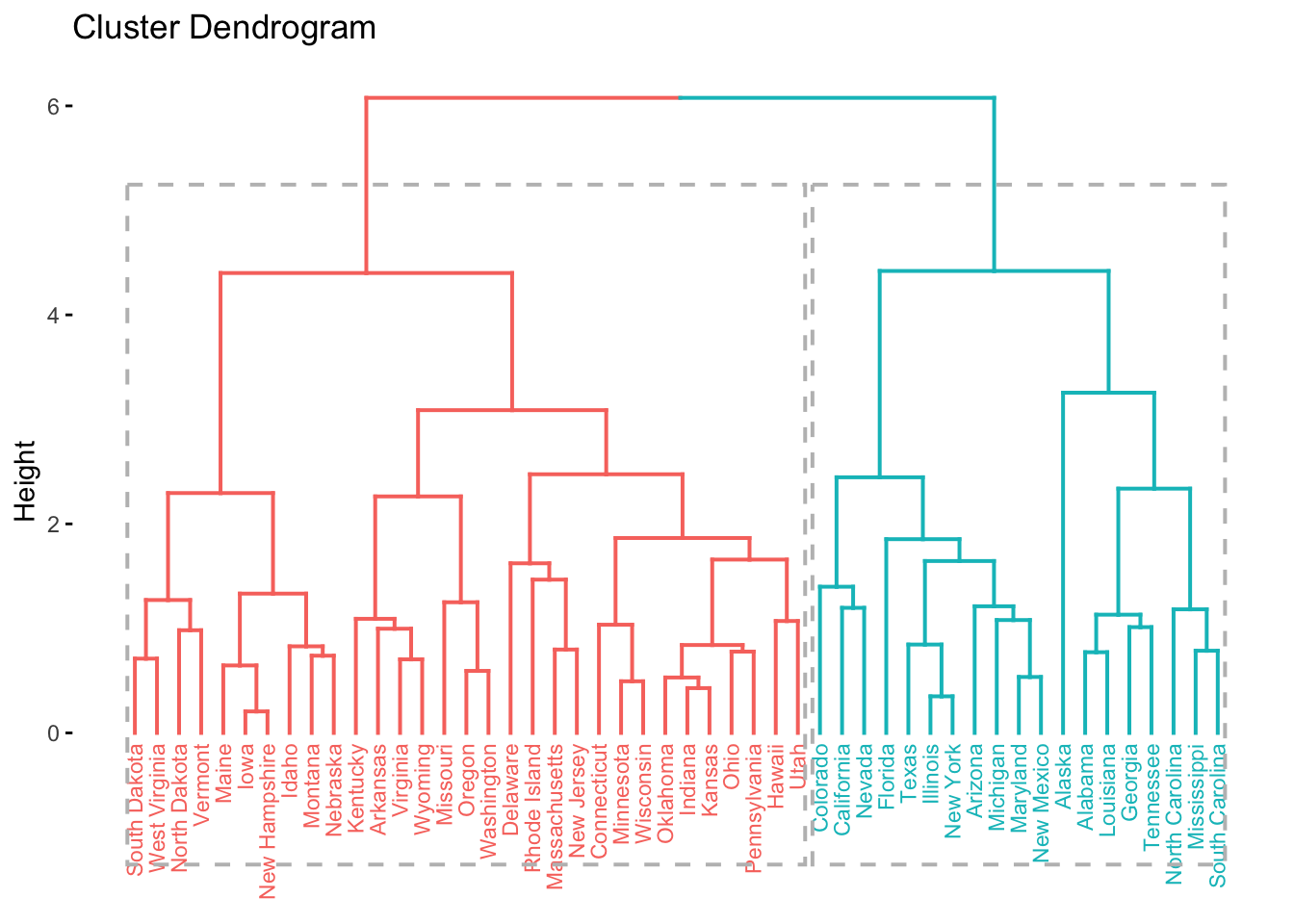
fviz_dend(hc, k = 2, # 2 grupos
cex = 0.6, # tamanho do texto/rótulo (label)
rect = TRUE # adiciona retângulos ao redor dos grupos
)
fviz_dend(hc, k = 3, # 3 grupos
cex = 0.6, # tamanho do texto/rótulo (label)
rect = TRUE # adiciona retângulos ao redor dos grupos
)
fviz_dend(hc, k = 4, # 4 grupos
cex = 0.6, # tamanho do texto/rótulo (label)
rect = TRUE # adiciona retângulos ao redor dos grupos
)
Exercício 10.3 Considere novamente o conjunto de dados pib. Crie dendrogramas com a função fviz_dend utilizando:
(a) dados originais e padronizados;
(b) diferentes distâncias;
(c) diferentes números de grupos.
Exercício 10.4 (E. L. Thorndike 1939, 156) apresenta uma tabela com a pountuação em uma escala de critérios com 10 itens para 7 cidades. As variáveis de critério estão descritas a seguir e podem ser obtidas diretamente do arquivo city-thorn.csv.
V1: Taxa de mortalidade infantil reversa
V2: Despesas com recreação
V3: Valor de escolas, parques, etc.
V4: Propriedade menos dívida
V5: Despesas com escolas
V6: Graduados do ensino médio
V7: Circulação da biblioteca
V8: Proporção de jovens de 16 e 17 anos na escola
V9: Telefones
V10: Casas com fiação elétrica
A partir dos dados fornecidos, crie um dendrograma segmentando as cidades em 4 grupos.