6.3 Regiões de Confiança
Regiões de confiança são os equivalentes multivariados aos intervalos de confiança univariados. Os intervalos de confiança são obtidos a partir de distribuições de probabilidade univariadas, e analogamente as regiões de confiança são derivadas de distribuições multivariadas. No caso bivariado geram-se elipses de confiança, no caso de dimensão 3 consideram-se elipsóides e para dimensões superiores consideram-se hiperelipsóides.
6.3.1 Gráficos 2D
Exemplo 6.4 Considere novamente o Exemplo 6.2.
## 'ellipsoid' in 2 dimensions:
## center = ( 4.771 43.754 ); squared ave.radius d^2 = 2
## and shape matrix =
## sweat sodium
## sweat 7.1463 34.08
## sodium 34.0801 587.42
## hence, area = 346.23
## 'ellipsoid' in 2 dimensions:
## center = ( 4.1678 10.3985 ); squared ave.radius d^2 = 2
## and shape matrix =
## sweat potassium
## sweat 9.5635 -6.4204
## potassium -6.4204 7.7782
## hence, area = 36.185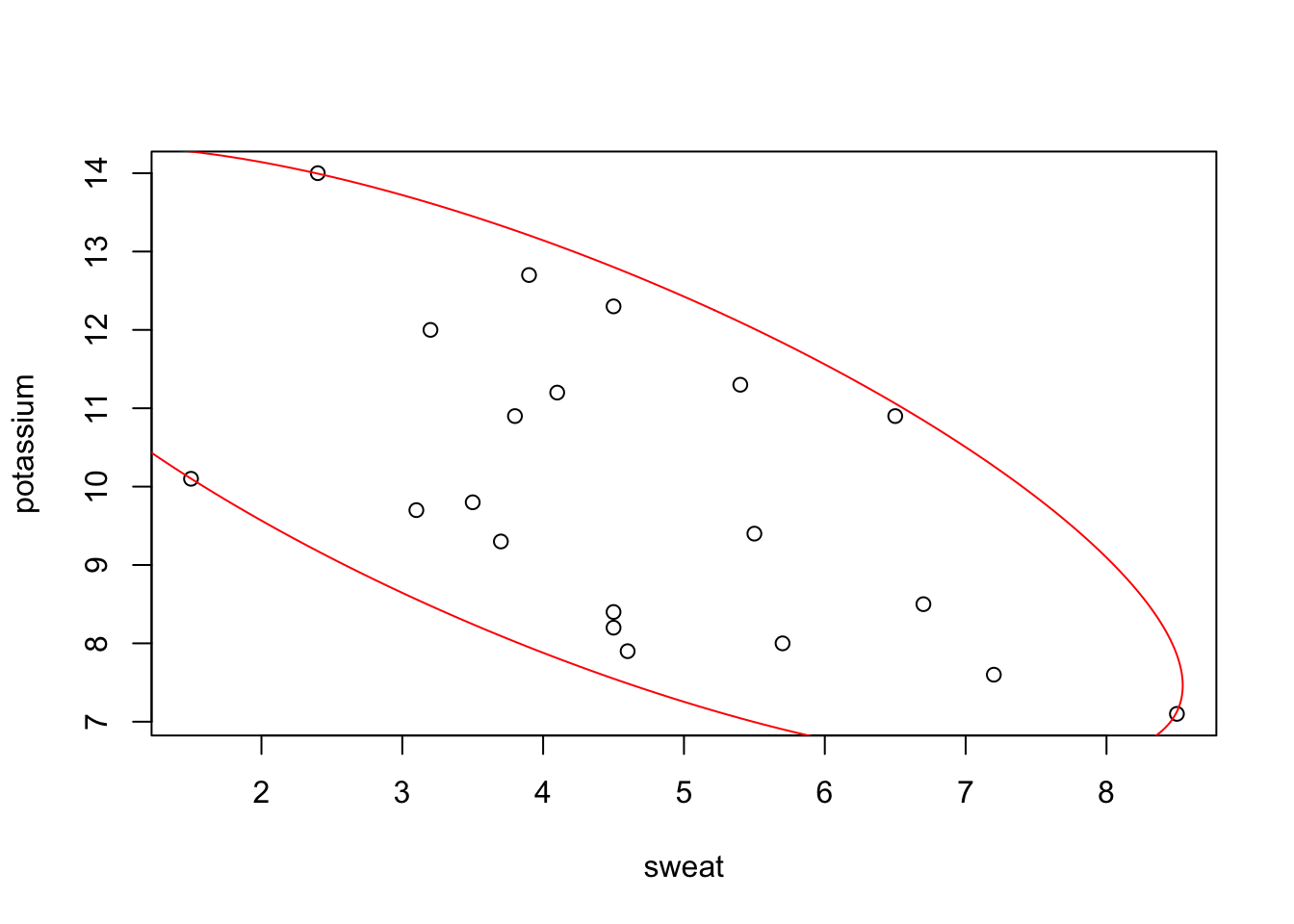
## 'ellipsoid' in 2 dimensions:
## center = ( 40.975 10.424 ); squared ave.radius d^2 = 2
## and shape matrix =
## sodium potassium
## sodium 497.415 -23.149
## potassium -23.149 6.477
## hence, area = 325.63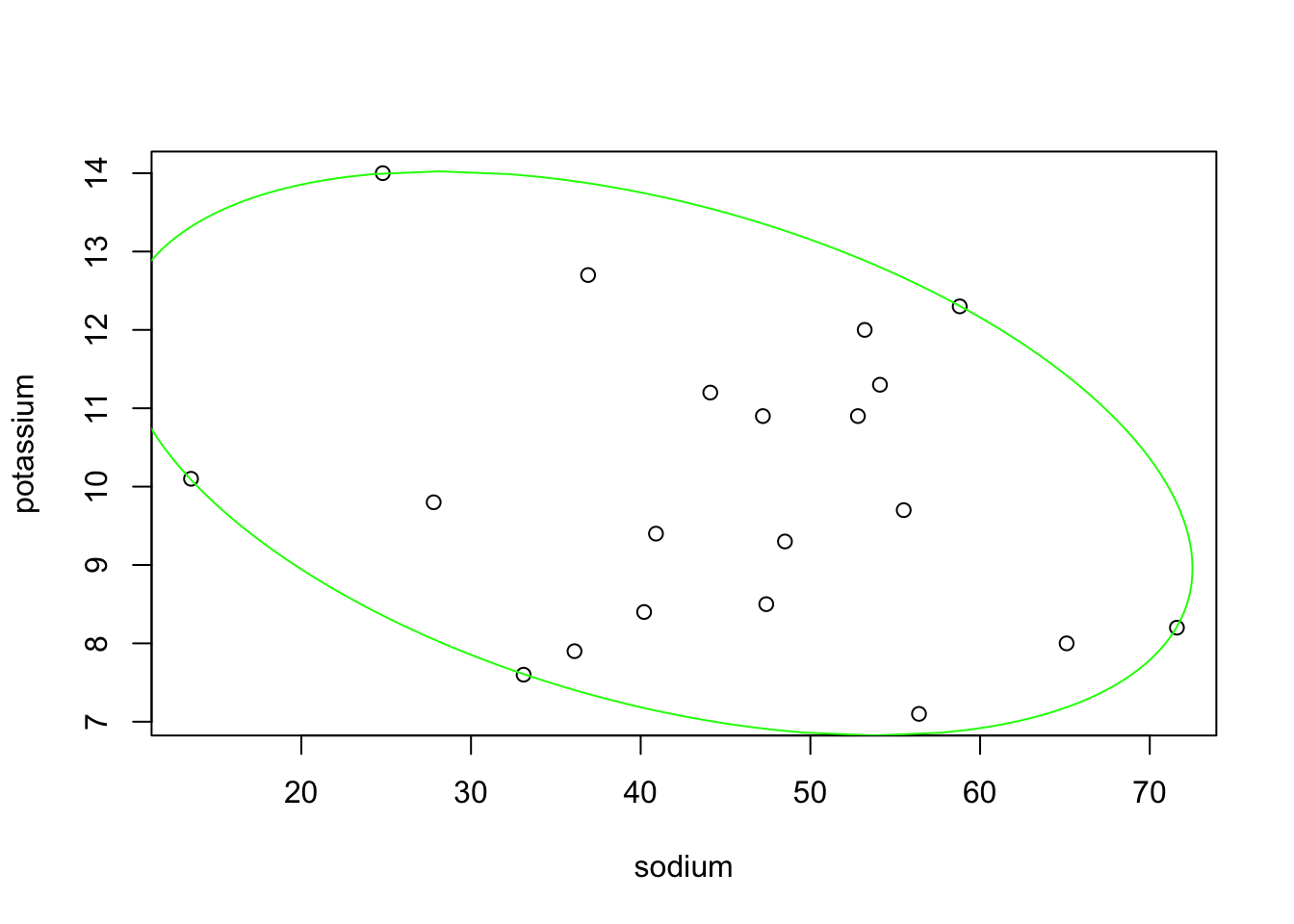
6.3.2 Gráficos 3D
Exemplo 6.5 Considere novamente o Exemplo 6.2.
library(rgl)
e3d <- ellipse3d(cov(sweat), colMeans(sweat))
if(type_book == 'bookdown::gitbook'){
rgl::plot3d(e3d, alpha = 0.6)
}
6.3.3 jocre
(Pallmann and Jaki 2017) trazem uma visão geral e comparação de todos os métodos para intervalos e regiões de confiança implementados no pacote jocre (Pallmann 2017). O autor, porém, recomenda cuidado no uso, pois [s]ome of the functionality has not yet been thoroughly tested.
| Método | Referência | Descrição |
|---|---|---|
standard.ind |
Região padrão ignorando correlação entre parâmetros. | |
standard.cor |
(Chew 1966) | Região padrão incorporando correlação entre parâmetros. |
emp.bayes |
(Casella and Hwang 1983) | Região empírica de Bayes. |
tost |
(Schuirmann 1987) | Intervalos de teste de dois unilaterais (Two One-Sided Test - TOST). |
limacon.asy |
(L. D. Brown, Casella, and Hwang 1995) | Região de volume mínimo esperado em forma de limaçon. |
limacon.fin |
(Berger and Hsu 1996) | Variante de amostra finita da região de volume mínimo esperado. |
tseng.brown |
(Tseng and Brown 1997) | Região pseudo-empírica de Bayes. |
hotelling |
(W. Wang, Hwang, and Dasgupta 1999) | Região tipo Hotelling. |
tseng |
(Tseng 2002) | Região de comprimento de intervalo mínimo esperado. |
boot.kern |
(Pallmann and Jaki 2017) | Método de bootstrap não paramétrico usando estimativa de densidade do kernel. |
Exemplo 6.6 Considere novamente o Exemplo 6.2.
library(jocre)
sweat <- read.table('https://filipezabala.com/data/sweat.txt', header = TRUE)
cset(sweat[,1:2], method = 'standard.ind')## Parameter estimates and projected boundaries of the 2-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.64 -6.919 16.199
## sodium 45.40 33.841 56.959## Parameter estimates and projected boundaries of the 2-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.64 -6.919 16.199
## sodium 45.40 33.841 56.959## Parameter estimates and 90% simultaneous confidence intervals:
##
## Estimate Lower Upper
## sweat 4.640 4.136 5.144
## sodium 45.400 41.204 49.596
## potassium 9.965 9.400 10.530## Parameter estimates and projected boundaries of the 2-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.64 -0.859 5.787
## sodium 45.40 0.333 50.618## Parameter estimates and projected boundaries of the 3-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.640 -22.411 27.128
## sodium 45.400 0.424 48.985
## potassium 9.965 -19.367 29.194## Parameter estimates and projected boundaries of the 2-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.64 Inf Inf
## sodium 45.40 Inf Inf## Parameter estimates and projected boundaries of the 3-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.640 -56.632 56.786
## sodium 45.400 -56.611 56.807
## potassium 9.965 -56.521 56.571## Parameter estimates and projected boundaries of the 3-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.640 -56.632 56.786
## sodium 45.400 -56.611 56.807
## potassium 9.965 -56.521 56.571## Parameter estimates and projected boundaries of the 2-dimensional
## 90% simultaneous confidence region:
##
## Estimate Lower Upper
## sweat 4.64 3.887 5.425
## sodium 45.40 39.045 51.741Proporções
Quando trabalha-se com \(k\) proporções deve-se respeitar a condição de que a soma destas proporções deve ser igual a 1, i.e., \(\sum_{i=1}^k p_i = 1\). Isto nem sempre é feito na prática, e pode-se utilizar o método apresentado por (Zabala 2009), que leva em consideração a estrutura de dependência.
Exemplo 6.7 No caso de um cenário eleitoral com \(k=3\) candidatos, suponha que em uma amostra de \(n=100\) eleitores o candidato A tenha 60% das intenções de voto, B 30% e C 10%. Ao contrário do que sugerem os institutos de pesquisa, não é recomendado comparar intervalos de confiança independentes por violar a condição de que a soma das proporções deve ser igual a 1, levando a conclusões incoerentes conforme discutido na Seção 3.2.4 de (Zabala 2009). A função simplex3d do pacote desempateTecnico traz uma ferramenta para visualização da elipse de confiança desenhada sobre um 2-simplex, i.e., um triângulo no espaço tridimensional onde a soma das proporções é igual a 1. Podem-se definir algumas regiões relevantes dentro do simplex, onde as linhas verdes indicam as regiões onde as proporções são iguais a 50%, e as linhas vermelhas se interseccionam no ponto \(\left( \tfrac{1}{3},\tfrac{1}{3},\tfrac{1}{3} \right)\).
- \(A\) ganha no 1º turno, \(B\) em 2º lugar
- \(A\) ganha no 1º turno, \(C\) em 2º lugar
- \(B\) ganha no 1º turno, \(A\) em 2º lugar
- \(B\) ganha no 1º turno, \(C\) em 2º lugar
- \(C\) ganha no 1º turno, \(A\) em 2º lugar
- \(C\) ganha no 1º turno, \(B\) em 2º lugar
- \(A\) e \(B\) no 2º turno, \(A\) na frente
- \(A\) e \(B\) no 2º turno, \(B\) na frente
- \(A\) e \(C\) no 2º turno, \(A\) na frente
- \(A\) e \(C\) no 2º turno, \(C\) na frente
- \(B\) e \(C\) no 2º turno, \(B\) na frente
- \(B\) e \(C\) no 2º turno, \(C\) na frente
Considerando \(\alpha=5\%\) pode-se indicar pela elipse de confiança que 1 (\(A\) ganha no 1º turno, \(B\) em 2º lugar) e 7 (\(A\) e \(B\) no 2º turno, \(A\) na frente) são os cenários mais prováveis.
Exercício 6.3 Considere a função simplex3d do pacote desempateTecnico.
(a) Fixe \(\alpha=5\%\) e gere gráficos com tamanhos de amostra \(n\) iguais a 10, 50, 500 e 2000. O que você observa?
(b) Fixe \(n=100\) e gere gráficos com valores de significância \(\alpha\) iguais a \(0.5\%\), \(1\%\), \(5\%\) e \(10\%\). O que você observa?
(c) Se as linhas verdes indicam 50% dos votos, qual a sua opinião sobre um cenário eleitoral com \(p_a = 0.43\), \(p_b = 0.37\) e \(p_c = 0.2\), obtidos com uma amostra de tamanho 500 considerando \(\alpha=0.05\)?