11.14 Análise no domínio da frequência
Segundo (Pollock 1999, 15), o domínio de frequência da análise de séries temporais “é uma herança de Euler (1707–1783), d’Alembert (1717–1783), Lagrange (1736–1813) e Fourier (1768–1830)”.
11.14.1 Transformada de Fourier
The essence of Fourier analysis is the representation of a set of data in terms of sinusoidal functions. (Bloomfield 1976, 7)
A transformada de Fourier converte uma função de entrada \(f\) no domínio do tempo em uma nova função \(\hat{f}\) no domínio da frequência. Em outras palavras, a função original pode ser considerada como sendo “amplitude dado o tempo”, e a transformada de Fourier da função é “amplitude dada a frequência”.
A função stats::fft() calcula a Transformada Discreta de Fourier (DFT) de uma matriz com a transformada rápida de Fourier (FFT) (Cooley and Tukey 1965).
Exemplo 11.60 Adaptado da documentação de stats::fft().
## [1] 10+0i -2+2i -2+0i -2-2i## [1] 1+0i 2+0i 3+0i 4+0iExemplo 11.61 Adaptado da documentação de forecast::fourier().
# Using Fourier series for a "ts" object, K is chosen to minimize the AICc
library(forecast)
library(tidyverse)
deaths.model <- forecast::auto.arima(USAccDeaths,
xreg = forecast::fourier(USAccDeaths, K = 5),
seasonal = FALSE)
deaths.fcast <- forecast::forecast(deaths.model,
xreg = forecast::fourier(USAccDeaths, K = 5, h = 36))
autoplot(deaths.fcast) + xlab('Year')
Exercício 11.38 Veja
11.14.2 Periodograma
The periodogram is a summary description based on a representation of an observed time series as a superposition of sinusoidal waves of various frequencies. (Diggle 1990, 47)
[T]he features that show statistical regularity are known as the spectrum of the series. (Bloomfield 1976, 160)
The spectral density function is the theoretical counterpart of the (empirical) spectrum. (Bloomfield 1976, 182)
(Schuster 1898, 24–25) propõe o periodograma como uma “representação de uma grandeza variável que corresponderá ao ‘espectro’ de uma radiação luminosa”.
A função stats::spectrum() estima a densidade espectral de uma série temporal. É uma função wrapper (empacotada) que chama os métodos spec.pgram() (periodograma via FFT com suavizador opcional) e spec.ar() (periodograma via modelo AR). Autores como (Thomson 1990), porém, alertam fortemente que os espectros de modelos AR podem ser enganosos.
Conforme a documentação, stats::spec.pgram() calcula o periodograma usando uma transformada rápida de Fourier (Cooley and Tukey 1965). Opcionalmente suaviza o resultado com uma série de suavizadores de Daniell (Daniell 1946) modificados (médias móveis que dão peso 1/2 aos valores finais). O argumento spans admite um vetor de números inteiros ímpares fornecendo as larguras dos suavizadores de Daniell modificados a serem usados para suavizar o periodograma. Pelo fato de o periodograma bruto não ser um estimador consistente da densidade espectral, será dada preferência para estimadores suavizados.
# janela gráfica 2x2
par(mfrow = c(2,2))
# Ruído branco gaussiano
set.seed(42); z <- rnorm(100)
stats::spectrum(z)
stats::spectrum(z, spans = 3)
stats::spectrum(z, spans = c(3,3))
stats::spectrum(z, spans = c(3,5))
# Luteinizing Hormone in Blood Samples
stats::spectrum(lh)
stats::spectrum(lh, spans = 3)
stats::spectrum(lh, spans = c(3,3))
stats::spectrum(lh, spans = c(3,5))
# Monthly corticosteroid drug subsidy in Australia from 1991 to 2008
stats::spectrum(h02)
stats::spectrum(h02, spans = 3)
stats::spectrum(h02, spans = c(3,3))
stats::spectrum(h02, spans = c(3,5))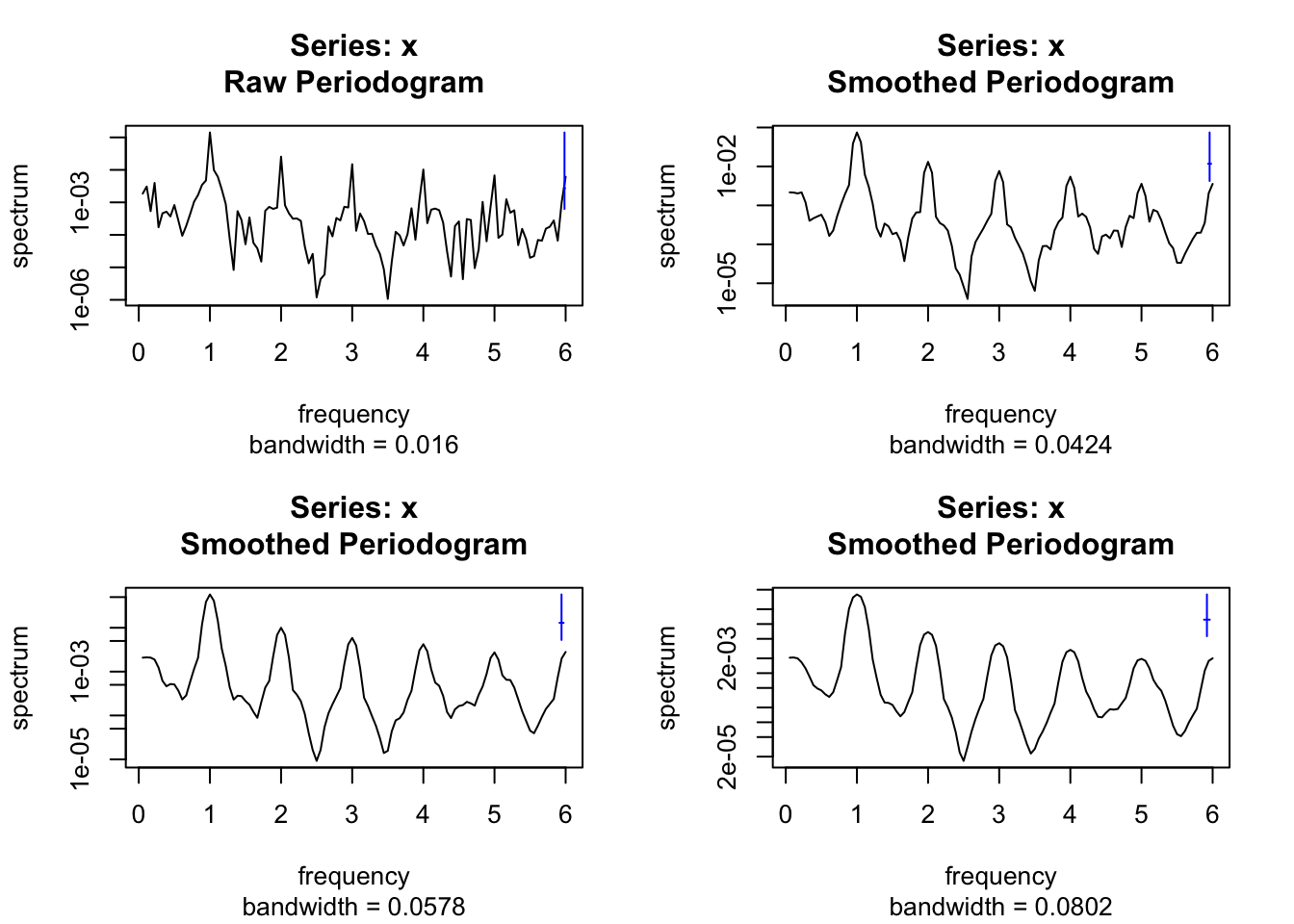
# bivariate example - plots marginal spectra: now plot coherency and phase
mfdeaths <- ts.union(mdeaths, fdeaths)
mfdeaths.spc <- spec.pgram(mfdeaths, spans = c(3,3))
plot(mfdeaths.spc, plot.type = 'coherency')
plot(mfdeaths.spc, plot.type = 'phase')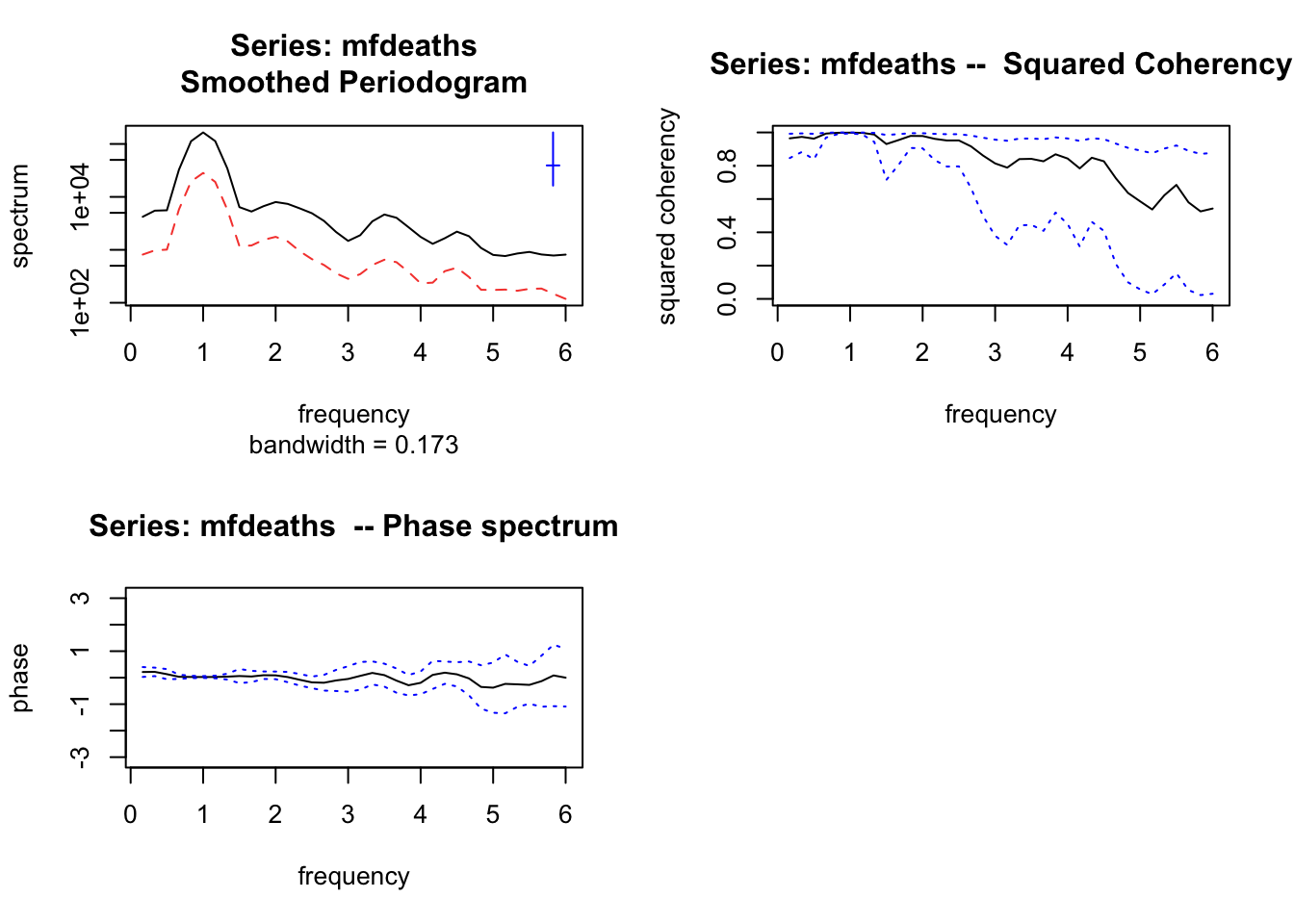
Exercício 11.39 Considere o periodograma.
- Leia a lição 6.1 The Periodogram do curso STAT 510 - Applied Time Series Analysis da Penn State.
- Leia a discussão What is the confidence interval calculated in a spectral density periodogram in R?.
- Leia o Capítulo 7 Introduction to time series analysis in the frequency domain de Edward L. Ionides.
Exemplo 11.62 Adaptado da saída do ChatGPT com o seguinte prompt em 2024-10-29.
É importante entender como o domínio de frequência na abordagem de previsão de séries temporais pode melhorar os modelos usuais de séries temporais. Como podemos usar as frequências encontradas por periodogramas para construir modelos melhores? Como programar isso em R e Python?
# Carregar os dados e pacotes
library(forecast)
# Gerar uma série temporal de exemplo
set.seed(42)
data <- ts(rnorm(100) + sin(2 * pi * 1:100 / 20))
# Periodograma
spec.pgram(data, spans = c(3,3), taper = 0, log = 'no')
# Identificar a frequência principal
freq <- which.max(spec.pgram(data, plot = FALSE)$spec)
# Ajustar modelo SARIMA com a frequência dominante
model_sarima <- forecast::Arima(data, order = c(1,0,0),
seasonal = list(order = c(1, 1, 0),
period = freq))
# Gráfico
forecast::autoplot(forecast::forecast(model_sarima, h = 20))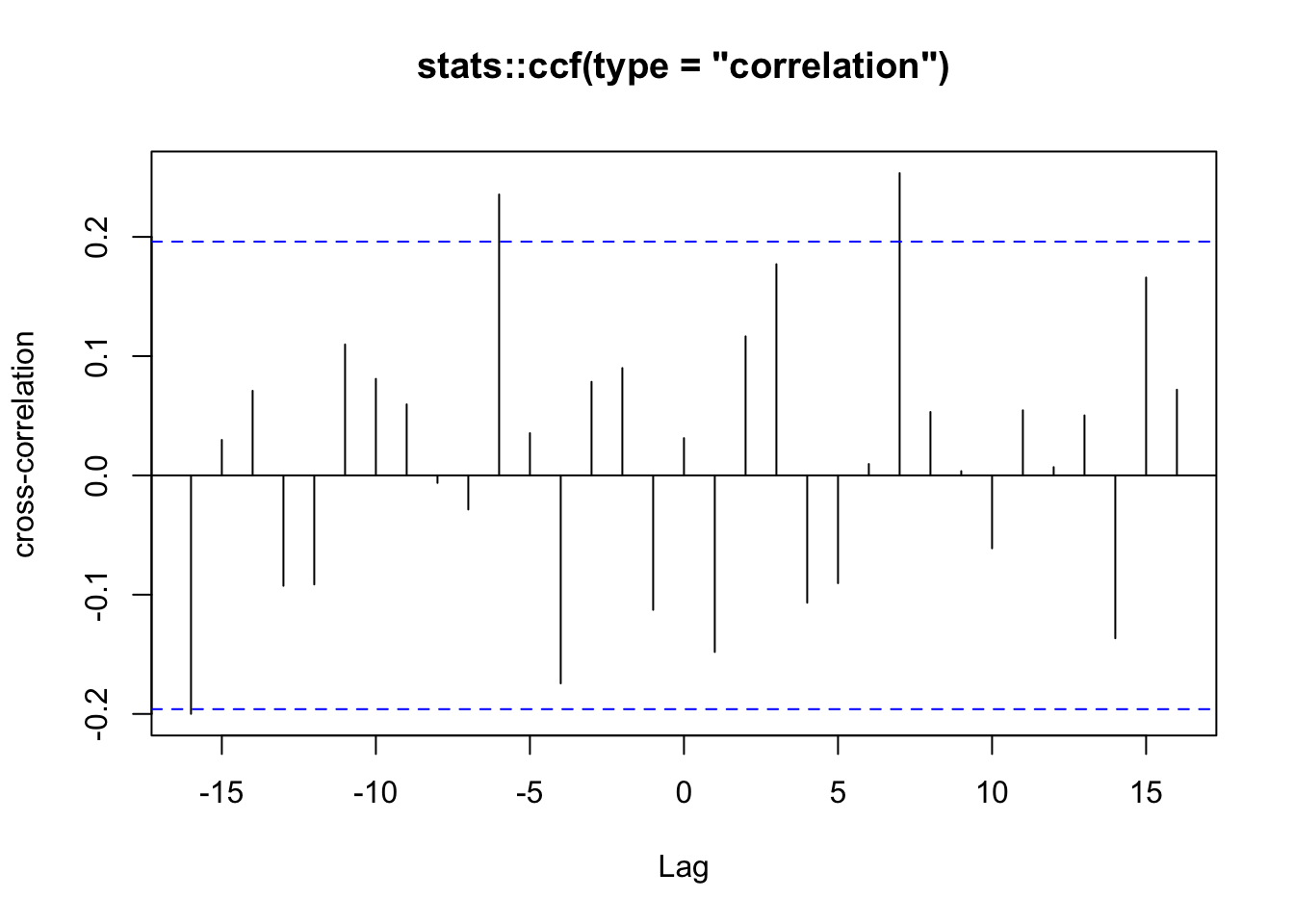
# Comparando com forecast::auto.arima
forecast::autoplot(forecast::forecast(auto.arima(data), h = 20))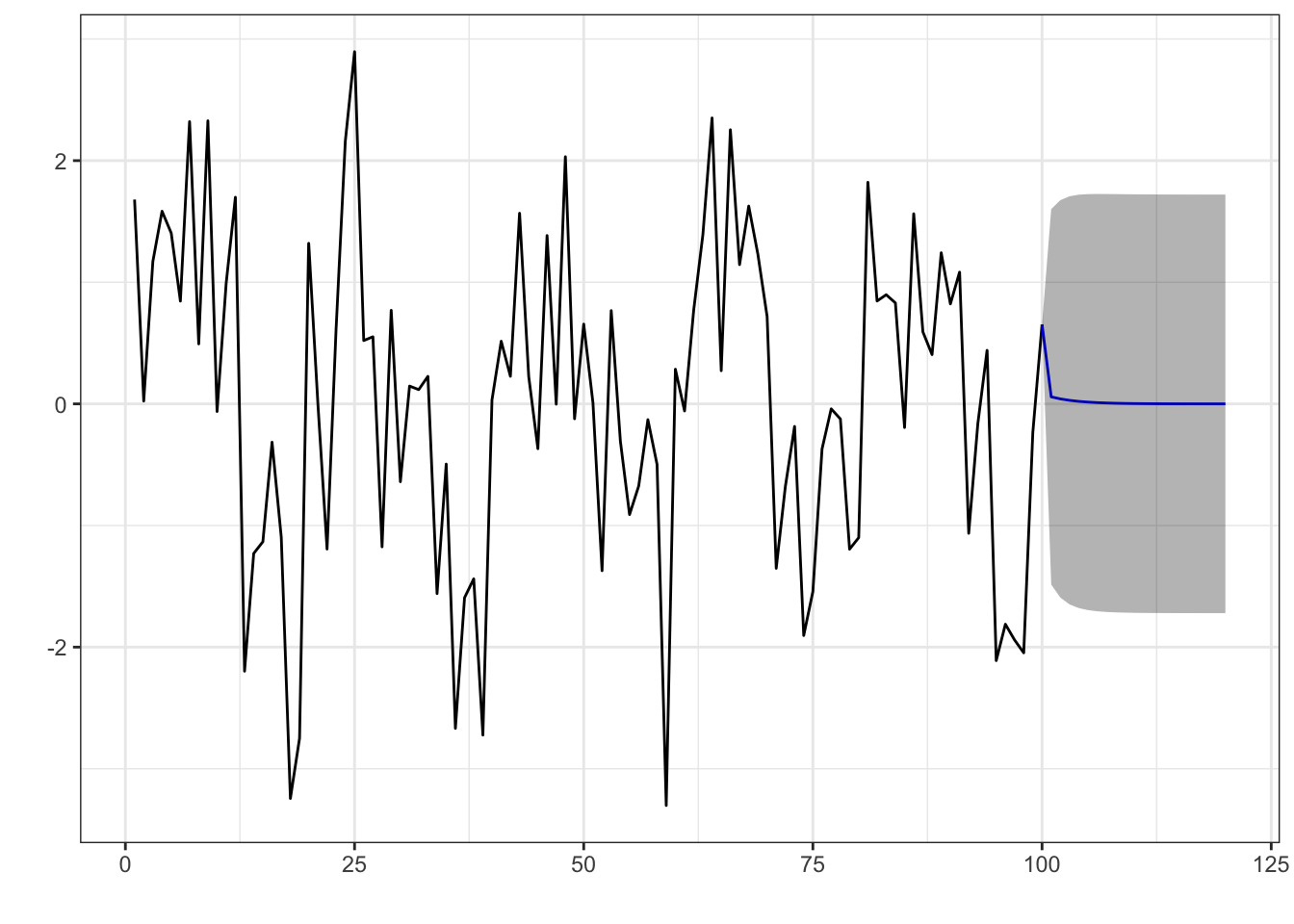
Exercício 11.40 Considere o Exemplo 11.62.
- Repita a modelagem utilizando a estratégia treino-teste 80-20. Compare os EQMs de previsão para o modelo SARIMA com a frequência dominante e aquele obtido via
forecast::auto.arima(). - Aplique a estratégia do item anterior para as bases de dados já discutidas:
fpp2::oilfpp2::h02datasets::lhdatasets::lynxdatasets::airmiles
11.14.3 Regressão harmônica
[H]armonic regression: least squares regression on a sinusoid or sinusoids. (Bloomfield 1976,viii)
Seguindo (Bloomfield 1976, 9–10), \[\begin{equation} y_t = \mu + R \cos(\omega t + \phi) + \varepsilon_t \tag{11.43} \end{equation}\]
\[\begin{equation} y_t = \mu + A \cos(\omega t) + B \sin(\omega t) + \varepsilon_t \tag{11.44} \end{equation}\]
\[\begin{equation} A = R \cos \phi \tag{11.45} \end{equation}\]
\[\begin{equation} B = -R \sin \phi \tag{11.45} \end{equation}\]
11.14.3.1 Frequência \(\omega\) conhecida
Mínimos Quadrados
Para resolver a Eq. (11.43) via MQ deve-se minimizar \[\begin{equation} T(\mu,A,B) = \sum_{t=0}^{n-1} (y_t -\mu - A\cos(\omega t) - B\sin(\omega t))^2 \tag{11.46} \end{equation}\]
Aproximação
\[\begin{equation} \tilde{\mu} = \frac{1}{n} \sum_{t=0}^{n-1} y_t \tag{11.47} \end{equation}\]
\[\begin{equation} \tilde{A} = \frac{2}{n} \sum_{t=0}^{n-1} (y_t - \tilde{\mu}) \cos(\omega t) \tag{11.48} \end{equation}\]
\[\begin{equation} \tilde{B} = \frac{2}{n} \sum_{t=0}^{n-1} (y_t - \tilde{\mu}) \sin(\omega t) \tag{11.49} \end{equation}\]
\[\begin{equation} \tilde{\phi} = \left\{ \begin{array}{l l} \arctan \left( -\frac{\tilde{B}}{\tilde{A}} \right) & \quad \tilde{A}>0 \\ \arctan \left( -\frac{\tilde{B}}{\tilde{A}} \right) - \pi & \quad \tilde{A}<0, \tilde{B}>0 \\ \arctan \left( -\frac{\tilde{B}}{\tilde{A}} \right) + \pi & \quad \tilde{A}<0, \tilde{B} \le 0 \\ -\pi/2 & \quad \tilde{A}=0, \tilde{B}>0 \\ \pi/2 & \quad \tilde{A}=0, \tilde{B}<0 \\ \text{arbitrário} & \quad \tilde{A}=0, \tilde{B}=0 \\ \end{array} \right. \tag{11.50} \end{equation}\]
\[\begin{equation} \tilde{R} = \frac{\tilde{A}}{\cos \tilde{\phi}} = -\frac{\tilde{B}}{\sin \tilde{\phi}} \tag{11.51} \end{equation}\]
Exemplo 11.63 Outro exemplo gerado pelo ChatGPT através do prompt descrito no Exemplo 11.62. Novamente foi sugerido set.seed(42), pelo jeito ele conhece o Guia do Mochileiro das Galáxias e 2 Reis 2:23-24.
# Gerando uma série temporal com padrões sazonais
set.seed(42)
y <- ts(sin(2 * pi * seq(1, 100) / 12) + rnorm(100), frequency = 12)
# Calculando o periodograma
periodograma <- spec.pgram(y, log = 'no', spans = c(3,3),
main = 'Periodograma da Série Temporal')
# Identificando a frequência principal \omega
omega <- periodograma$freq[which.max(periodograma$spec)]
cat('Frequência principal:', omega, '\n')## Frequência principal: 0.96# Modelando com função harmônica
modelo <- lm(y ~ sin(2 * pi * omega * 1:100) + cos(2 * pi * omega * 1:100))
# Previsão
previsao_mq <- predict(modelo, newdata = data.frame(1:100))Aplicando as Eq. (11.47), (11.48), (11.49), (11.50) e (11.51) com os dados do Exemplo 11.63.
n <- length(y)
mu_tilde <- mean(y)
sum_A <- 0
sum_B <- 0
for(i in 0:(n-1)){
sum_A <- sum_A + (y[i+1]-mu_tilde)*cos(omega*i)
sum_B <- sum_B + (y[i+1]-mu_tilde)*sin(omega*i)
}
A_tilde <- (2/n) * sum_A
B_tilde <- (2/n) * sum_B
# Veja Bloomfield 1976, 12
if(A_tilde > 0){
phi_tilde <- atan(-B_tilde/A_tilde)
} else if(A_tilde < 0 & B_tilde > 0){
phi_tilde <- atan(-B_tilde/A_tilde)-pi
} else if(A_tilde < 0 & B_tilde <= 0){
phi_tilde <- atan(-B_tilde/A_tilde)+pi
} else if(A_tilde == 0 & B_tilde > 0){
phi_tilde <- -pi/2
} else if(A_tilde == 0 & B_tilde < 0){
phi_tilde <- pi/2
} else{
phi_tilde <- 0
}
R_tilde <- A_tilde/cos(phi_tilde)
# Previsão via Eq. 12.46
previsao_aprox <- mu_tilde + R_tilde*cos(omega*1:n + phi_tilde)
# Gráficos
plot(y, type = 'l', main = 'Modelos de Previsão com Frequência Principal')
lines(previsao_mq, col = 'red', lwd = 2)
lines(previsao_aprox, col = 'blue', lwd = 2)
legend('bottomright',
legend = c('MQ ChatGPT', 'Aproximado'),
col = c('red','blue'), # cores
lty = 1, # linha contínua
lwd = 2, # espessura
bty = 'n', # sem borda na legenda
text.col = c('red','b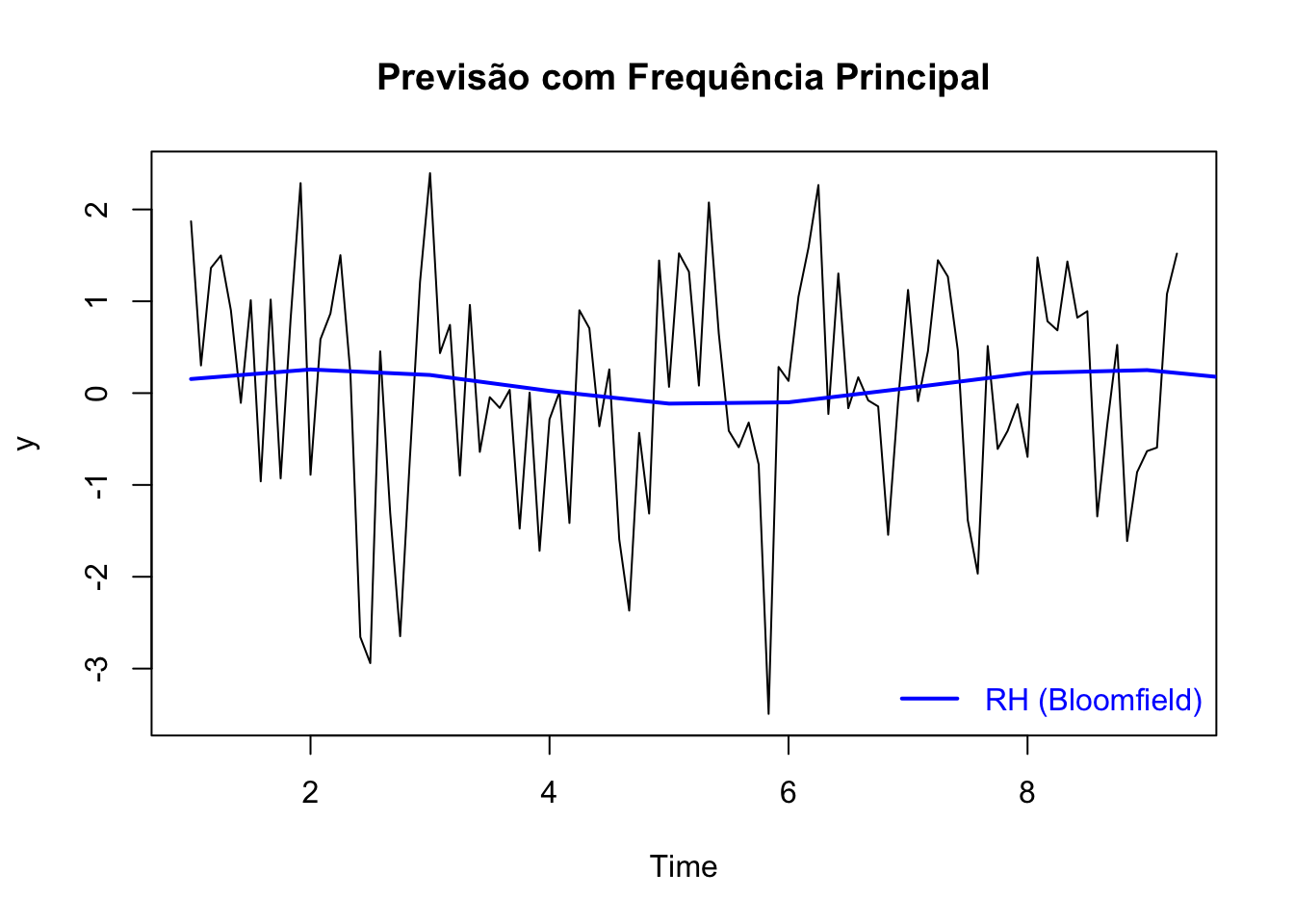lue'))
11.14.3.2 Frequência \(\omega\) desconhecida
Veja (Bloomfield 1976, 18–20).
Exercício 11.41 Considere o prompt do Exemplo 11.62.
- Faça uma avaliação dos resultados no ChatGPT, realizando as alterações e melhorias que julgar adequadas.
- Teste os códigos apresentados em R e Python.
11.14.4 Ondaleta (Wavelet)
Wavelets, as the name suggests, are ‘little waves’. (Nason 2008, 1)
https://en.wikipedia.org/wiki/Wavelet
library(wavethresh)
y <- c(1,1,7,9,2,8,8,6)
ywd <- wavethresh::wd(y, filter.number = 1, family = 'DaubExPhase')
ywd## Class 'wd' : Discrete Wavelet Transform Object:
## ~~ : List with 8 components with names
## C D nlevels fl.dbase filter type bc date
##
## $C and $D are LONG coefficient vectors
##
## Created on : Wed Apr 9 17:05:06 2025
## Type of decomposition: wavelet
##
## summary(.):
## ----------
## Levels: 3
## Length of original: 8
## Filter was: Haar wavelet
## Boundary handling: periodic
## Transform type: wavelet
## Date: Wed Apr 9 17:05:06 2025