12.16 Medindo fluxo de informação
12.16.1 Informação
- Seção 5.3.1
- (Hartley 1928)
- (Dimpfl and Peter 2013, 86)
12.16.2 Entropia (de Shanon)
- Seção 5.3.2
- (Shannon 1948, 11)
12.16.3 Divergência de Kullback-Leibler
- Seção 5.3.4
12.16.4 Entropia de Rényi
(Rényi 1961, 549) define a entropia de Rényi de ordem \(\alpha\) da distribuição discreta \(\mathcal{P} = (p_1,\ldots,p_n)\) por \[\begin{equation} H_{\alpha} = \frac{1}{1-\alpha} \log_2 \left( \sum_{i=1}^{n} p_{i}^{\alpha} \right) \tag{12.52} \end{equation}\] para \(\alpha>0\) e \(\alpha \ne 1\), onde a medida de entropia de Shannon é o limite quando \(\alpha \rightarrow 1\).
12.16.5 Entropia de transferência
In conclusion, the new transfer entropy is able to detect the directed exchange of information between two systems. (Schreiber 2000, 464)
Transfer entropy (…) is a nonparametric measure of asymmetric information transfer between time series. (Behrendt et al. 2019, 2)
(Bossomaier et al. 2016) apresentam uma introdução à entropia de transferência, ou fluxo de informação, proposta por (Schreiber 2000). (Behrendt et al. 2019) apontam que o método de entropia de transferência foi aplicado em diversas áreas como engenharia biomédica, neurociência, ou para extrair informações de dados de mídia social. Há exemplo específicos como
- detectar diferenças entre dados de eletroencefalografia (EEG) de indivíduos saudáveis e epilépticos
- analisar a onda circumpolar antártica
- examinar a transmissão de informações entre mercados financeiros
(Schreiber 2000, 462) define taxa de entropia como \[\begin{equation} h_I = -\sum p(i_{n+1},i_{n}^{(k)}) \, \log p(i_{n+1}|i_{n}^{(k)}) \tag{12.53} \end{equation}\] onde \(i_{n}^{(k)} = (i_{n}, \ldots, i_{n-k+1})\).
O autor argumenta que como \(p(i_{n+1}|i_{n}^{(k)}) = p(i_{n+1}^{(k+1)})/p(i_{n}^{(k)})\), “esta é apenas a diferença entre as entropias de Shannon dos processos dados por \(k+1\) e \(k\) vetores de atraso dimensionais construídos a partir de \(I\)”: \[\begin{equation} h_I = H_{I^{(k+1)}} - H_{I^k} \tag{12.54} \end{equation}\]
(Schreiber 2000, 462) mede o quão incorreta é a suposição de que o processo \(J\) não tem qualquer influência nas probabilidades de transição do processo \(I\) através da entropia de transferência (de Shannon) \[\begin{equation} T_{J \rightarrow I}(k,l) = \sum p(i_{n+1}, i_{n}^{(k)}, j_{n}^{(l)}) \, \log \frac{p(i_{n+1} | i_{n}^{(k)}, j_{n}^{(l)})}{p(i_{n+1}, i_{n}^{(k)})} \tag{12.55} \end{equation}\] onde dentre “[a]s escolhas mais naturais para \(l\)” \((l=k\) ou \(l=1)\) prefere \(l=1\) “por motivos computacionais”.
(Jizba, Kleinert, and Shefaat 2012) formulam o “conceito de entropia de transferência de Rényi como uma medida de informação que é transferida apenas entre certas partes das distribuições subjacentes” a partir das escort distributions de (Beck and Schögl 1993, 53) na forma \(\phi_{\alpha}(j) = \frac{p^{\alpha}(j)}{\sum_i p^{\alpha}(i)}\), com \(\alpha > 0\). \[\begin{equation} T_{J \rightarrow I}^{\text{Rényi}}(k,l) = \frac{1}{1-\alpha} \log \left( \frac{\sum_i \phi_{\alpha}(i_{n}^{(k)}) p^{\alpha}(i_{n+1}|i_{n}^{(k)})}{\sum_{i,j} \phi_{\alpha}(i_{n}^{(k)},j_{n}^{(l)}) p^{\alpha}(i_{n+1}|i_{n}^{(k)},j_{n}^{(l)})} \right) \tag{12.56} \end{equation}\] Ao contrário da entropia de transferência de Shannon, a entropia de transferência de Rényi pode resultar em valores negativos, indicando que conhecer o histórico de \(J\) revela um risco ainda maior do que seria indicado se apenas se conhecesse o histórico de \(I\).
(Marschinski and Kantz 2002, 278) propõem a entropia de transferência efetiva (effective transfer entropy) “como a diferença entre a entropia de transferência usual calculada para a série empírica e a entropia de transferência calculada para a mesma série, mas com a série J embaralhada” (shuffled) na forma \[\begin{equation} ET_{J \rightarrow I}(k,l) = T_{J \rightarrow I}(k,l) - T_{J_{\text{shuffled}} \rightarrow I}(k,l) \tag{12.57} \end{equation}\] Conforme vinheta, “o embaralhamento implica em desenhar aleatoriamente valores da série temporal \(J\) e realinhá-los para gerar uma nova série temporal. Este procedimento destrói as dependências da série temporal \(J\), bem como as dependências estatísticas entre \(J\) e \(I\)”, podendo ser usadas como um estimador para o viés induzido por esses pequenos efeitos de amostra.
Exercício 12.37 Mostre que \(i_{n+1}^{(k+1)} = (i_{n+1}, \ldots, i_{n-k+1})\).
12.16.6 Biblioteca RTransferEntropy
A biblioteca RTransferEntropy (Behrendt et al. 2019) permite quantificar e testar o fluxo de informação entre duas séries temporais com entropias de transferência de Shannon e Rényi. Conforme vinheta, “[u]m aspecto central do pacote fornecido é permitir inferência estatística e testes de hipóteses no contexto da entropia de transferência”. Note a equivalência \(\alpha \equiv q\).
Exemplo 12.32 Adaptado da vinheta de RTransferEntropy.
library(RTransferEntropy)
# simulando
set.seed(42)
n <- 2500
x <- rep(0, n + 1)
y <- rep(0, n + 1)
for (i in 2:(n + 1)) {
x[i] <- 0.2 * x[i - 1] + rnorm(1, 0, 2)
y[i] <- x[i - 1] + rnorm(1, 0, 2)
}
x <- x[-1]
y <- y[-1]
# gráficos
plot(x[1:(n-1)],y[2:n], xlab = 'X_t-1', ylab = 'Y_t')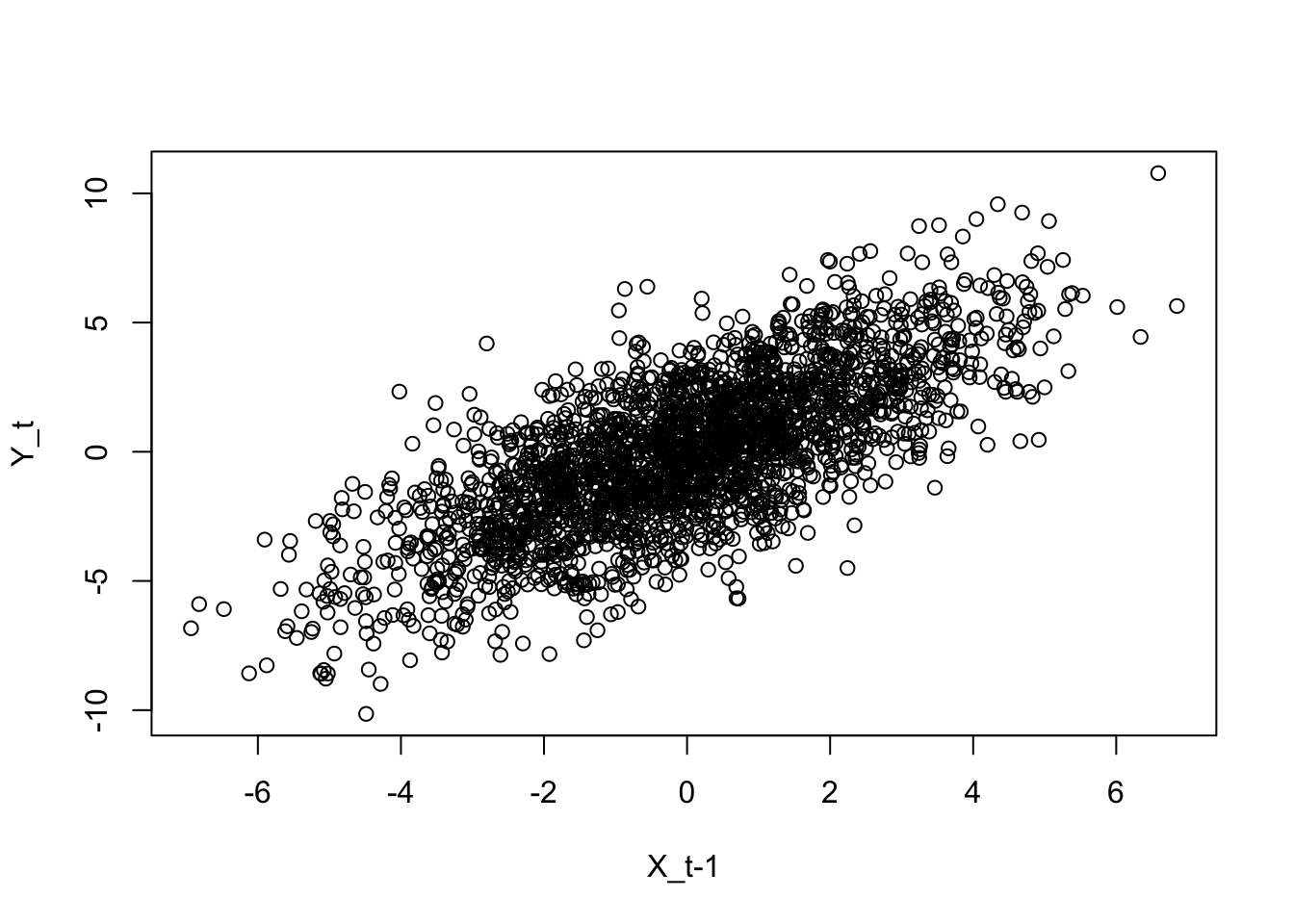
# calculando entropia de transferência
library(future)
plan(multisession)
shannon_te <- transfer_entropy(x, y, seed = 42)## Shannon's entropy on 8 cores with 100 shuffles.
## x and y have length 2500 (0 NAs removed)
## [calculate] X->Y transfer entropy
## [calculate] Y->X transfer entropy
## [bootstrap] 300 times
## Done - Total time 3.18 seconds## Shannon Transfer Entropy Results:
## -----------------------------------------------------------
## Direction TE Eff. TE Std.Err. p-value sig
## -----------------------------------------------------------
## X->Y 0.1137 0.1109 0.0012 0.0000 ***
## Y->X 0.0044 0.0013 0.0012 0.1033
## -----------------------------------------------------------
## Bootstrapped TE Quantiles (300 replications):
## -----------------------------------------------------------
## Direction 0% 25% 50% 75% 100%
## -----------------------------------------------------------
## X->Y 0.0008 0.0020 0.0026 0.0034 0.0070
## Y->X 0.0006 0.0020 0.0027 0.0036 0.0083
## -----------------------------------------------------------
## Number of Observations: 2500
## -----------------------------------------------------------
## p-values: < 0.001 '***', < 0.01 '**', < 0.05 '*', < 0.1 '.'