12.8 Covariâncias e correlações

12.8.1 Definições

Stationary time series are unchanging in respect to their general structure. (Wold 1938, 1)

Estacionariedade estrita: ocorre quando uma série temporal é invariante a deslocamentos (shifts), i.e., para qualquer subconjunto de tamanho \(n\) e qualquer inteiro \(\tau\), \((Y_{t_1},Y_{t_2},\ldots,Y_{t_n})\) tem a mesma distribuição conjunta de \((Y_{t_1+\tau},Y_{t_2+\tau},\ldots,Y_{t_n+\tau})\) (Peng 2020).

Estacionariedade fraca ou de segunda ordem: ocorre se a média for constante e a covariância entre quaisquer dois valores depender apenas da diferença de tempo entre esses dois valores (e não do valor de \(t\) em si), i.e., \(E(Y_t)=\mu\) e \(Cov(Y_t,Y_{t+\tau})=\gamma_{\tau}\) (Peng 2020).

Ruído branco: “The simplest possible example of a stationary random sequence is white noise. This consists of a sequence of mutually independent random variables, each with mean zero and finite variance \(\sigma^2\). Its autocovariance function is \(\gamma(t,s)=\sigma^2\)” if \(t=s\), 0 if \(t \ne s\). (Diggle 1990, 13–14)

Ruído branco gaussiano: É um ruído branco com distribuição normal.

Exemplo 12.8 A função stats::arima.sim() permite simular séries de ruído branco. Note que não se rejeita a normalidade de 94.3% das séries simuladas com \(\alpha=0.05\), uma vez que rand.gen = rnorm. Veja ?stats::arima.sim() para mais detalhes.

M <- 1000
wn <- vector(length = M)
for(i in 1:M){
  set.seed(i); sim <- arima.sim(model = list(order = c(0, 0, 0)), n = 200)
  wn[i] <- shapiro.test(sim)$p.value
}
sum(wn > 0.05)/M
## [1] 0.943
boxplot(wn)
abline(h = 0.05, col = 'red')

12.8.2 Lags

As funções tsDyn::autopairs() e tsDyn::autotriples() (M. Stigler 2019), (Fabio Di Narzo, Aznarte, and Stigler 2024) apresentam diversas alternativas de visualização de lags de séries temporais. A função plot_lag a seguir é um exercício para reforçar o entendimento das notações matemática e computacional requeridas.

plot_lag <- function(x, max.lag = 12){
  par(mfrow=c(3,4))
  n <- length(x)
  for(i in 1:max.lag){
    plot(x[1:(n-i)],x[(i+1):n], main = paste0('k = ',i))
  }
  par(mfrow=c(1,1))
}
# ruído branco gaussiano
set.seed(42); z <- rnorm(100)
plot_lag(z)

# Luteinizing Hormone in Blood Samples
plot_lag(lh)

# Monthly corticosteroid drug subsidy in Australia from 1991 to 2008
plot_lag(h02)

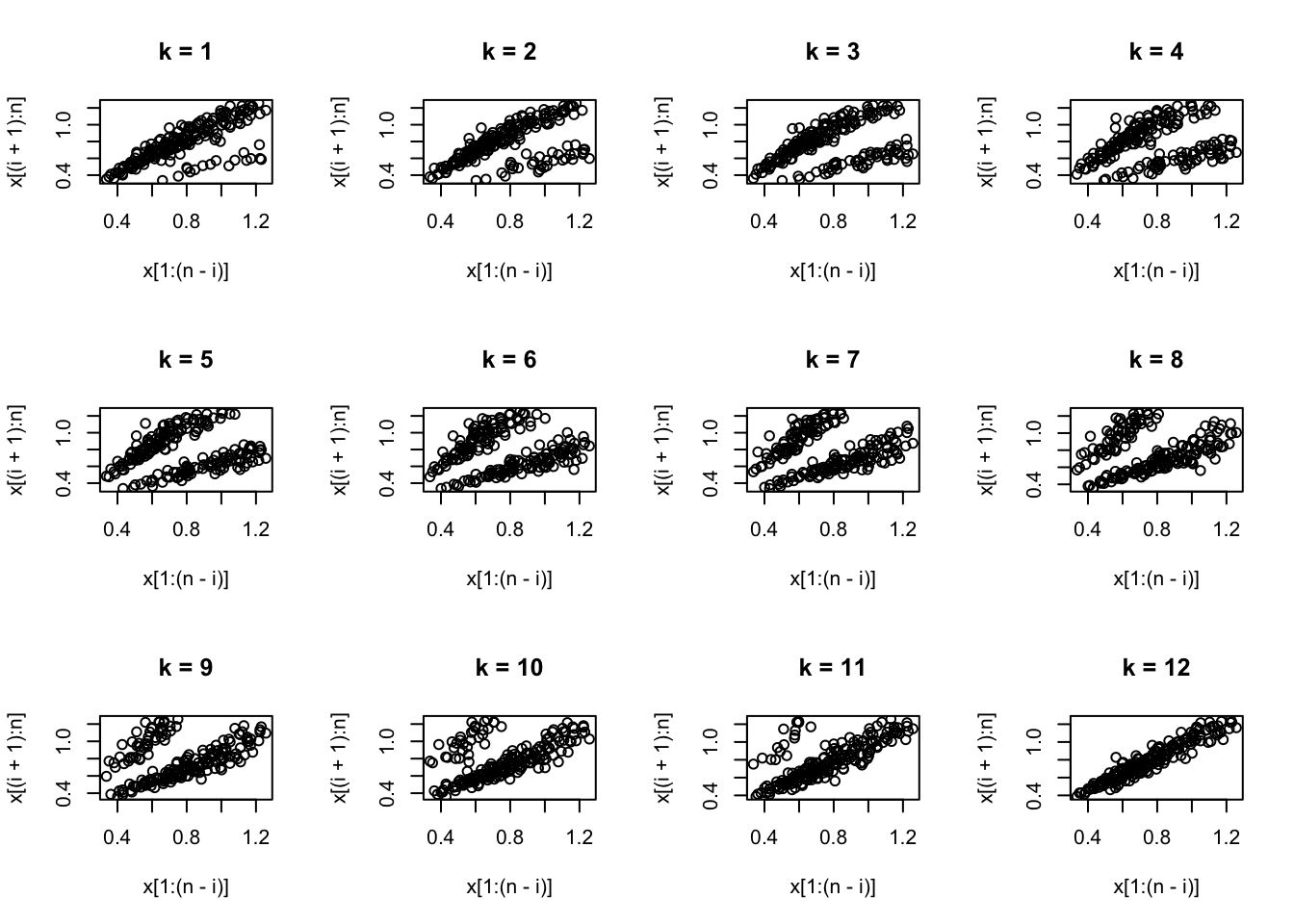
12.8.3 Autocovariância

Considerando a abordagem de (Diggle 1990, 34–39), a (função de) autocovariância amostral de uma variável aleatória estacionária \(Y_{t}\) para \(k\) inteiro é \[\begin{equation} \hat{\gamma}(k) = cov(Y_{t},Y_{t-k}) = \frac{1}{n} \sum_{i=k+1}^{n} (y_{i}-\bar{y}) (y_{i-k}-\bar{y}) \tag{12.7} \end{equation}\]

Conforme (Venables and Ripley 2002, 390), o divisor \(n\) é utilizado mesmo que haja \(n-|t|\) termos, de forma a garantir que a sequência \(\hat{\gamma}(k)\) é a sequência de covariâncias de uma série temporal estacionária de segunda ordem.

12.8.4 Autocorrelação

Os lags que extrapolam os limites de acf() indicam a ordem \(q\) do \(ARIMA(p,d,q)\).

Sendo \(\gamma(0)\) a variância de cada \(Y_{t}\), a função de autocorrelação amostral é \[\begin{equation} \hat{\rho}(k) = cor(Y_{t},Y_{t-k}) = \frac{\hat{\gamma}(k)}{\hat{\gamma}(0)} \tag{12.8} \end{equation}\]

Propriedades

  1. \(\rho(k)=\rho(-k)\)
  2. \(-1 \le \rho(k) \le +1\)
  3. Se \(Y_{t}\) e \(Y_{t-k}\) são independentes, então \(\rho(k)=0\)

A função stats::acf() calcula (e por padrão plota) estimativas da função de autocorrelação e autocovariância amostrais. Apresenta por padrão \(\lceil 10\log_{10}n \rceil\) lag.max para séries univariadas, onde \(n\) é o número de observações.

# simulando ruído branco gausssiano
set.seed(42); z <- rnorm(100)
# autocovariância
acf(z, type = 'covariance', main = 'stats::acf(type = "covariance")')

# autocorrelação
acf(z, main = 'stats::acf()')

# autocorrelação
ro <- acf(lh, main = 'stats::acf()')

Os valores podem ser obtidos a partir as Eq. (12.7) e (12.8).

# autocovariância
acov <- function(x,k){
  n <- length(x)
  m <- mean(x)
  g <- 0
  for(i in (k+1):n){
    g <- g + (1/n)*(x[i]-m)*(x[i-k]-m)
  }
  return(g)
}
round(sapply(0:16, acov, x = lh), 5)
##  [1]  0.29792  0.17146  0.05417 -0.04313 -0.05208 -0.04458 -0.00625 -0.00604 -0.00125 -0.04042 -0.04583
## [12] -0.02896  0.01458  0.03562  0.02583  0.03542  0.04500
acf(lh, type = 'covariance', plot = FALSE)
## 
## Autocovariances of series 'lh', by lag
## 
##        0        1        2        3        4        5        6        7        8        9       10 
##  0.29792  0.17146  0.05417 -0.04312 -0.05208 -0.04458 -0.00625 -0.00604 -0.00125 -0.04042 -0.04583 
##       11       12       13       14       15       16 
## -0.02896  0.01458  0.03562  0.02583  0.03542  0.04500
# autocorelação
acor <- function(x,k){
  r <- acov(x,k)/acov(x,0)
  return(r)
}
round(sapply(0:16, acor, x = lh), 3)
##  [1]  1.000  0.576  0.182 -0.145 -0.175 -0.150 -0.021 -0.020 -0.004 -0.136 -0.154 -0.097  0.049  0.120
## [15]  0.087  0.119  0.151
acf(lh, type = 'correlation', plot = FALSE) # pode-se omitir type = 'correlation'
## 
## Autocorrelations of series 'lh', by lag
## 
##      0      1      2      3      4      5      6      7      8      9     10     11     12     13 
##  1.000  0.576  0.182 -0.145 -0.175 -0.150 -0.021 -0.020 -0.004 -0.136 -0.154 -0.097  0.049  0.120 
##     14     15     16 
##  0.087  0.119  0.151

A função stats::acf() também permite tratar os NA. na.pass retorna o objeto inalterado, veja exemplos aqui.

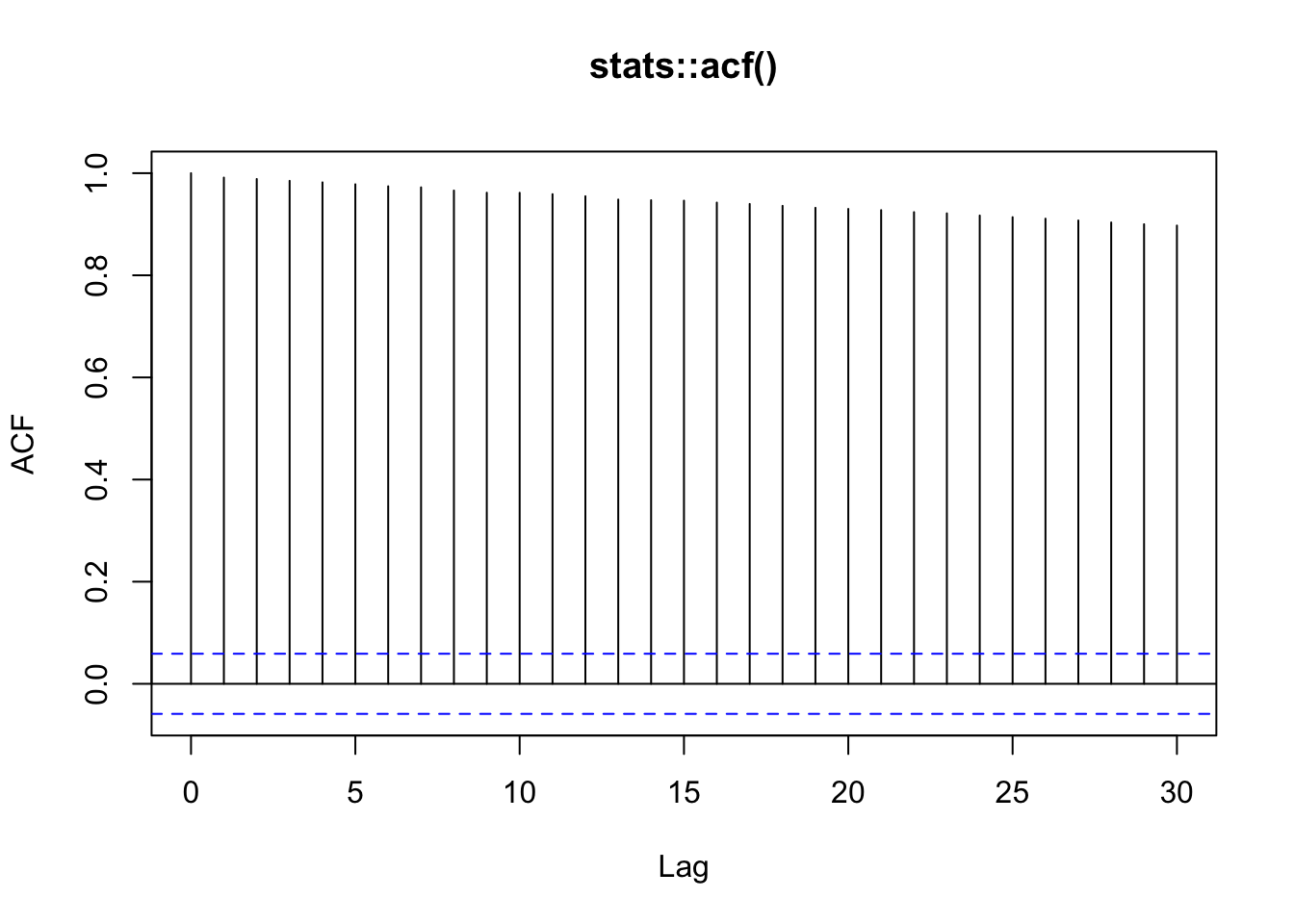
# autocovariância
acf(forecast::gold, type = 'covariance',
    na.action = na.pass,
    main = 'stats::acf(type = "covariance")')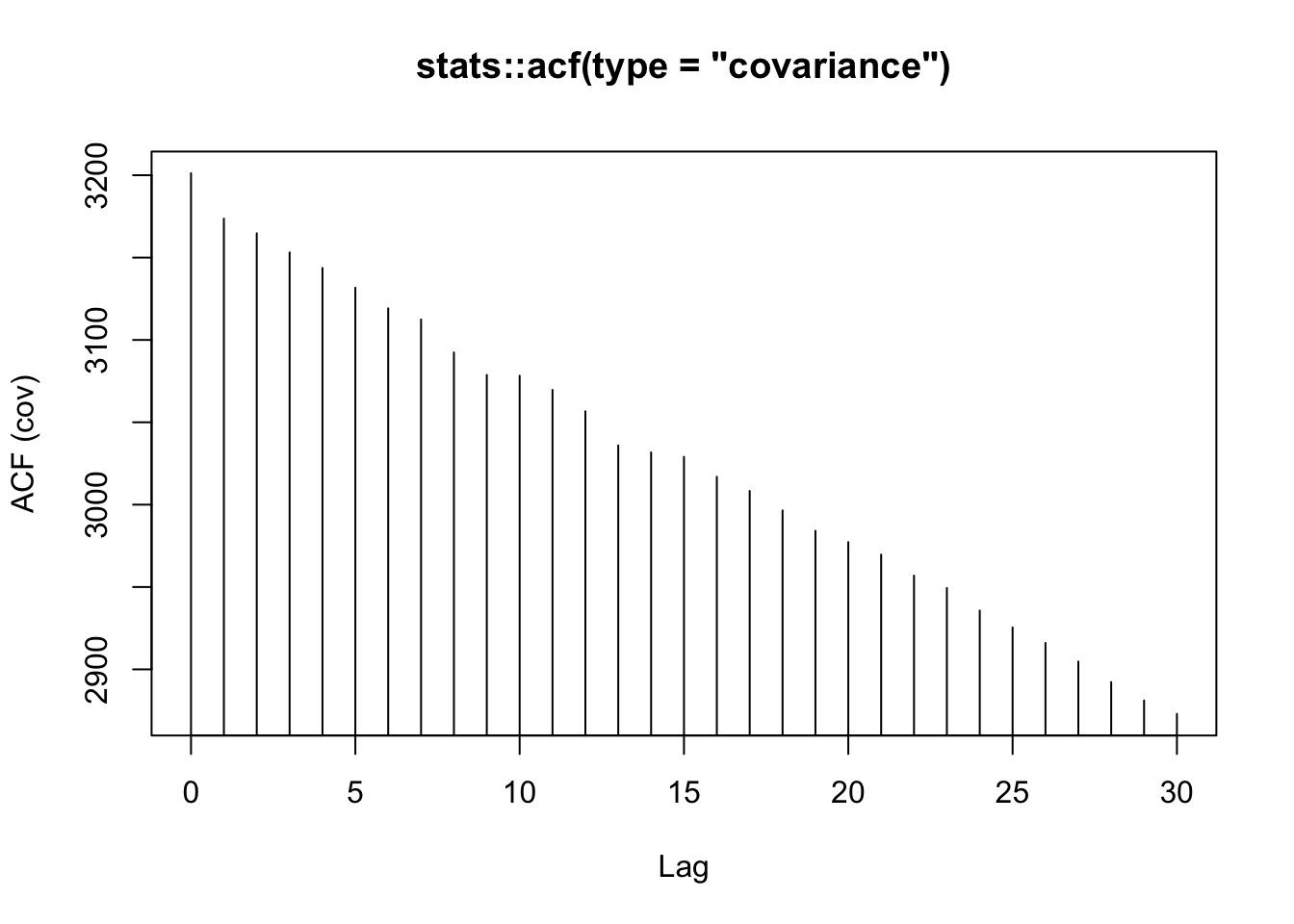

# autocorrelação
acf(forecast::gold, 
    na.action = na.pass, 
    main = 'stats::acf()')

12.8.5 Autocorrelação parcial

Os lags que extrapolam os limites de pacf() indicam a ordem \(p\) do \(ARIMA(p,d,q)\).

Seguindo a abordagem de (Enders 2014, 64–65), a autocorrelação parcial entre \(Y_{t}\) e \(Y_{t-k}\) elimina os efeitos dos valores intermediários \(Y_{t-1}\) e \(Y_{t-(k-1)}\). Sua estimativa pode ser obtida por \[\begin{equation} \hat{\phi}(1,1) = \hat{\rho}(1) \tag{12.9} \end{equation}\] \[\begin{equation} \hat{\phi}(k,k) = \frac{\hat{\rho}(k) - \sum_{i=1}^{k-1} \hat{\phi}(k-1,i) \; \hat{\rho}(k-i)}{1 - \sum_{i=1}^{k-1} \hat{\phi}(k-1,i) \; \hat{\rho}(i)}, \;\;\;\; k = 2,3,\ldots \tag{12.10} \end{equation}\] \[\begin{equation} \hat{\phi}(s,j) = \hat{\phi}(s-1,j) - \hat{\phi}(s,s) \hat{\phi}(s-1,s-j) \tag{12.11} \end{equation}\] onde \(j = 1,2,\ldots,s-1\). Note que \(\hat{\phi}(1,1) = corr(Y_{t},Y_{t-1})\) e \(\hat{\phi}(k,k) = corr(Y_{t}-\hat{Y}_{t},Y_{t-k}-\hat{Y}_{t-k})\), onde \(\hat{Y}_{t}\) e \(\hat{Y}_{t-k}\) são combinações lineares de \(\{Y_{t-1},\ldots,Y_{t-(k-1)}\}\) que minimizam o EQM de \(Y_{t}\) e \(Y_{t-k}\), respectivamente. Para mais detalhes veja (Durbin 1960).

As funções stats::pacf() e stats::acf(type = 'partial') calculam autocorrelações parciais. 

# simulando ruído branco gausssiano
set.seed(42); z <- rnorm(100)
pacf(z, na.action = na.pass, main = 'stats::pacf()')

pacf(lh, main = 'stats::pacf()')

pacf(h02, main = 'stats::pacf()')

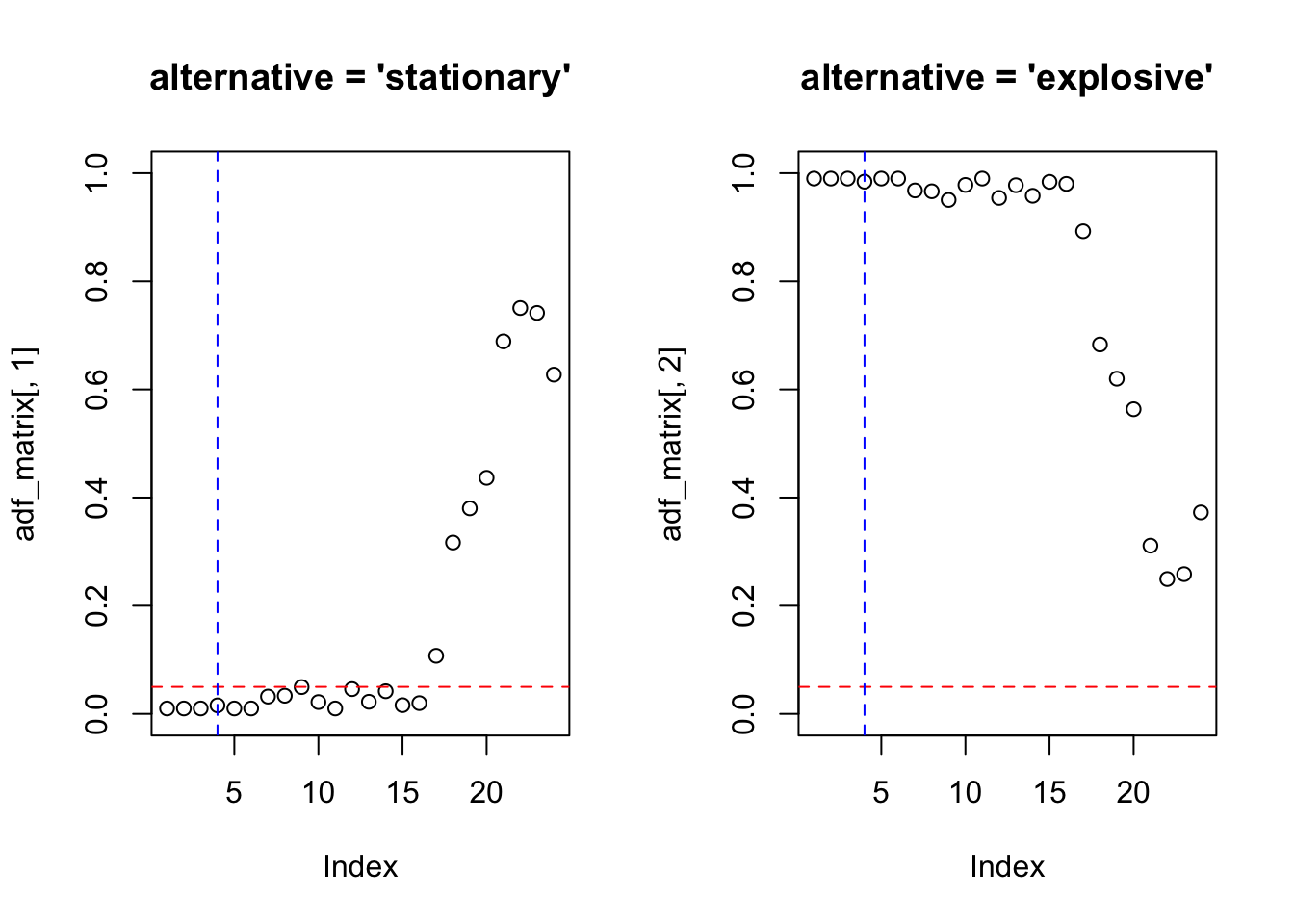
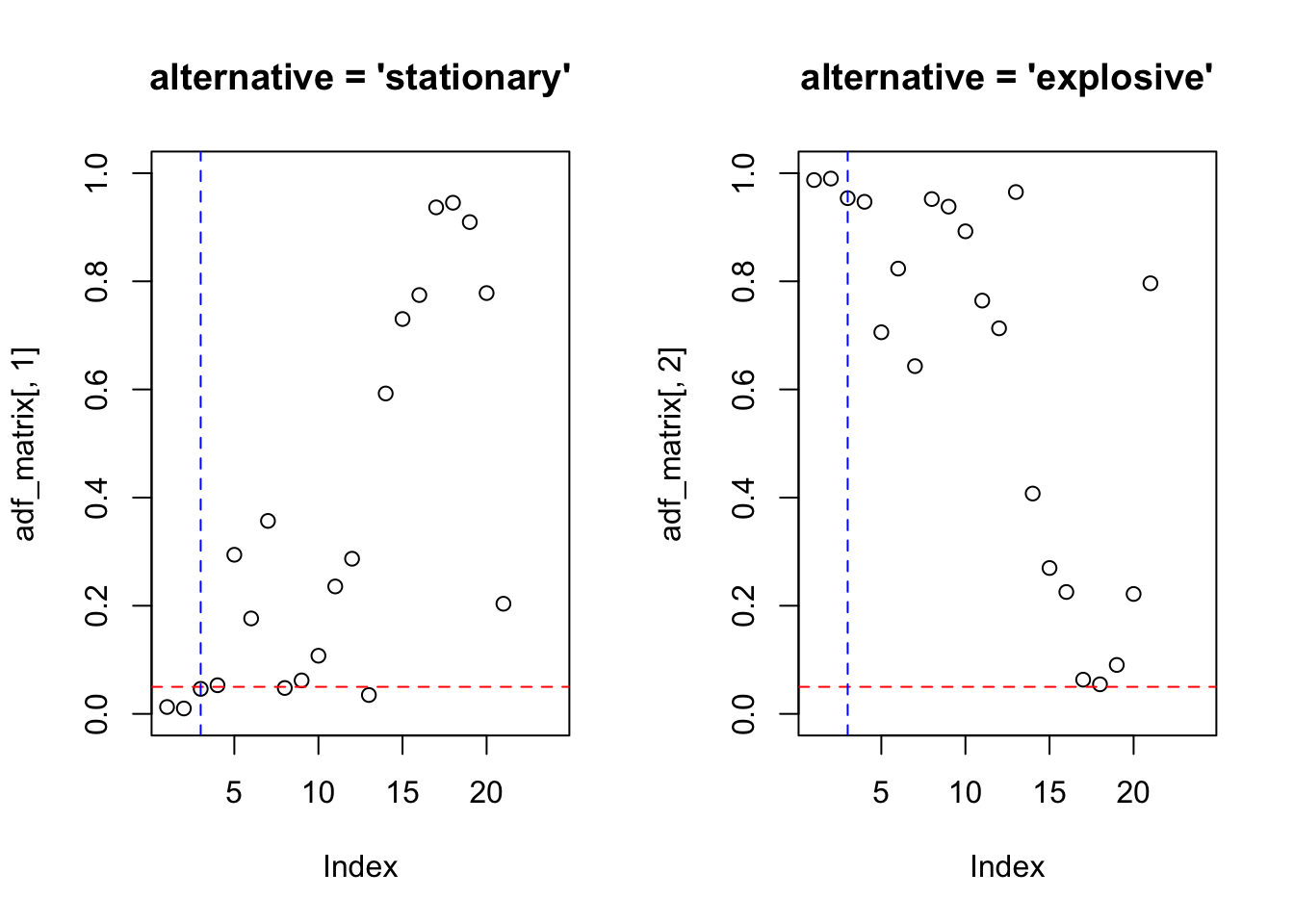
Exercício 12.16 Considere os conceitos de autocovariância, autocorrelação e autocorrelação parcial.

  1. Mostre que \(\gamma(0)\) é a variância de \(Y_{t}\).
  2. Verifique que \(\hat{\phi}(2,2) = \frac{\hat{\rho}(2) - \hat{\rho}(1)^2}{1 - \hat{\rho}(1)^2}\).
  3. Crie uma função em Python para calcular a autocovariância. Compare com stats::acf() e statsmodels.tsa.stattools.acovf().
  4. Crie uma função em Python para calcular a autocorrelação. Compare com stats::acf() e statsmodels.tsa.stattools.acf().
  5. Crie uma função em Python para calcular a autocorrelação. Compare com stats::pacf() e statsmodels.tsa.stattools.pacf().
  6. Veja https://www.youtube.com/watch?v=DeORzP0go5I.

Referências

Diggle, Peter J. 1990. Time Series: A Biostatistical Introduction. Oxford University Press. https://academic.oup.com/book/53018.
Durbin, James. 1960. “The Fitting of Time-Series Models.” Revue de l’Institut International de Statistique, 233–44. https://repository.lib.ncsu.edu/server/api/core/bitstreams/574e3264-2014-487c-9129-37ae4bea7d9e/content.
Enders, Walter. 2014. Applied Econometric Time Series. 4th ed. Wiley Series in Probability and Statistics.
Fabio Di Narzo, Antonio, Jose Luis Aznarte, and Matthieu Stigler. 2024. tsDyn: Time Series Analysis Based on Dynamical Systems Theory.
Peng, Roger D. 2020. “A Very Short Course on Time Series Analysis.” e-book. https://bookdown.org/rdpeng/timeseriesbook/.
Stigler, Matthieu. 2019. “Nonlinear time series in R: Threshold cointegration with tsDyn.” In Handbook of Statistics, Volume 41, edited by Hrishikesh D. Vinod and C. R. Rao, 42:229–64. Elsevier. https://doi.org/10.1016/bs.host.2019.01.008.
Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with s. Fourth. New York: Springer. https://www.stats.ox.ac.uk/pub/MASS4/.
Wold, Herman. 1938. “A Study in the Analysis of Stationary Time Series.” PhD thesis, Almqvist & Wiksell. https://archive.org/details/in.ernet.dli.2015.261682.