11.13 Séries temporais não lineares

O enfoque será nos métodos apresentados na biblioteca tsDyn (M. Stigler 2019), (Fabio Di Narzo, Aznarte, and Stigler 2024) que implementa modelos de séries temporais autorregressivas (AR) não lineares. Para uma introdução, veja a vinheta de tsDyn. Será utilizada a série temporal datasets::lynx de números anuais de capturas de linces entre 1821 e 1934 no Canadá.

11.13.1 Análise exploratória

11.13.1.1 Relações bivariadas e trivariadas

A função tsDyn::autopairs() mostra um gráfico de dispersão da série temporal \(x_t\) versus \(x_{t−lag}\).

library(tsDyn)
x <- log10(lynx)
autopairs(x, type = 'levels') # padrão lag = 1, type = 'levels'

autopairs(x, type = 'persp')

par(mfrow=c(2,2))
autopairs(x, type = 'regression')
autopairs(x, lag = 2, type = 'regression')
autopairs(x, lag = 3, type = 'regression')
autopairs(x, lag = 4, type = 'regression')

A função tsDyn::autotriples() apresenta \(x_t\) versus \((x_{t−lag1},x_{t−lag2})\).

library(tsDyn)
x <- log10(lynx)
autotriples(x) # padrão  lags = 1:2, type = 'levels'

autotriples(x, type = 'persp')

11.13.1.2 Linearidade

A função tsDyn::llar() (locally linear autoregressive fit) implementa o gráfico de ajuste autorregressivo linear local proposto por (Casdagli 1992). Este gráfico exibe o erro relativo feito pela previsão de valores de série temporal com modelos lineares de dimensão \(m\) e atraso de tempo \(d\) na forma

\[\begin{equation} y_{t+s} = \phi_0 + \phi_1 y_t + \ldots + \phi_m y_{t-(m-1)d} \tag{11.44} \end{equation}\]

estimado em pontos na esfera de raio \(\varepsilon\) ao redor de \(y_t^m\) para um intervalo de valores de \(\varepsilon\). Um mínimo atingido em valores relativamente pequenos de \(\varepsilon\) pode indicar que um modelo linear global seria inapropriado para a aproximação da dinâmica da série temporal.

\(d\) - Atraso de Tempo
  • O que é: O intervalo de tempo (em número de passos de tempo) entre as cópias defasadas sucessivas da sua série temporal.
  • O que faz: \(d\) determina o quão independentes as cópias defasadas são umas das outras.
\(m\) - Dimensão de Incorporação
  • O que é: O número de dimensões do seu espaço de estados reconstruído. Em outras palavras, quantas cópias defasadas da sua série temporal você usará.
  • O que faz: \(m\) determina quantos “eixos” seu grafo de reconstrução terá. Sua principal função é ser grande o suficiente para desdobrar o atrator sem autointerseções.

Exemplo 11.58 Exemplo do que são \(m\) e \(d\).

# Série temporal
x <- c(5, 8, 12, 9, 6, 10, 15, 11, 7, 13)

# Incorporação manual com m=3, d=2
m <- 3
d <- 2

# Matriz de incorporação
embedded_matrix <- matrix(NA, nrow = length(x) - (m-1)*d, ncol = m)

for(i in 1:nrow(embedded_matrix)) {
  embedded_matrix[i, ] <- x[seq(i, i + (m-1)*d, by = d)]
}

print("Série temporal:")
## [1] "Série temporal:"
print(x)
##  [1]  5  8 12  9  6 10 15 11  7 13
print("Matrix de incorporação (m=3, d=2):")
## [1] "Matrix de incorporação (m=3, d=2):"
print(embedded_matrix)
##      [,1] [,2] [,3]
## [1,]    5   12    6
## [2,]    8    9   10
## [3,]   12    6   15
## [4,]    9   10   11
## [5,]    6   15    7
## [6,]   10   11   13
Informação Mútua (Mutual Information)

Mutual information (…) measures the general dependence of two variables; therefore, it provides a better criterion for the choice of \(T\) than the autocorrelation function, which only measures linear dependence. (Fraser and Swinney 1986, 1135)

  • É uma medida de quanto informação uma variável contém sobre outra
  • Se duas variáveis são independentes, a informação mútua é zero
  • Se estão perfeitamente correlacionadas, a informação mútua é alta
Primeiro Mínimo
  • O primeiro mínimo da informação mútua representa o ponto ideal onde
    • Redundância mínima: \(y_t\) e \(y_{t+\tau}\) não são mais cópias quase idênticas
    • Dinâmica preservada: Ainda mantêm relação dinâmica significativa
    • Independência suficiente: As coordenadas são suficientemente independentes para revelar a estrutura multidimensional

Jornada do Average Mutual Information (AMI)

  • AMI Alta: \(y_t\) e \(y_{t+1}\) são “gêmeos idênticos”
  • AMI Decai: \(y_t\) e \(y_{t+2}\) são “irmãos”
  • PRIMEIRO MÍNIMO: \(y_t\) e \(y_{t+d}\) são “primos distantes mas ainda da mesma família”
  • AMI Sobe: \(y_t\) e \(y_{t+d+1}\)podem ter relação periódica
  • AMI Oscila: Padrões periódicos aparecem e desaparecem

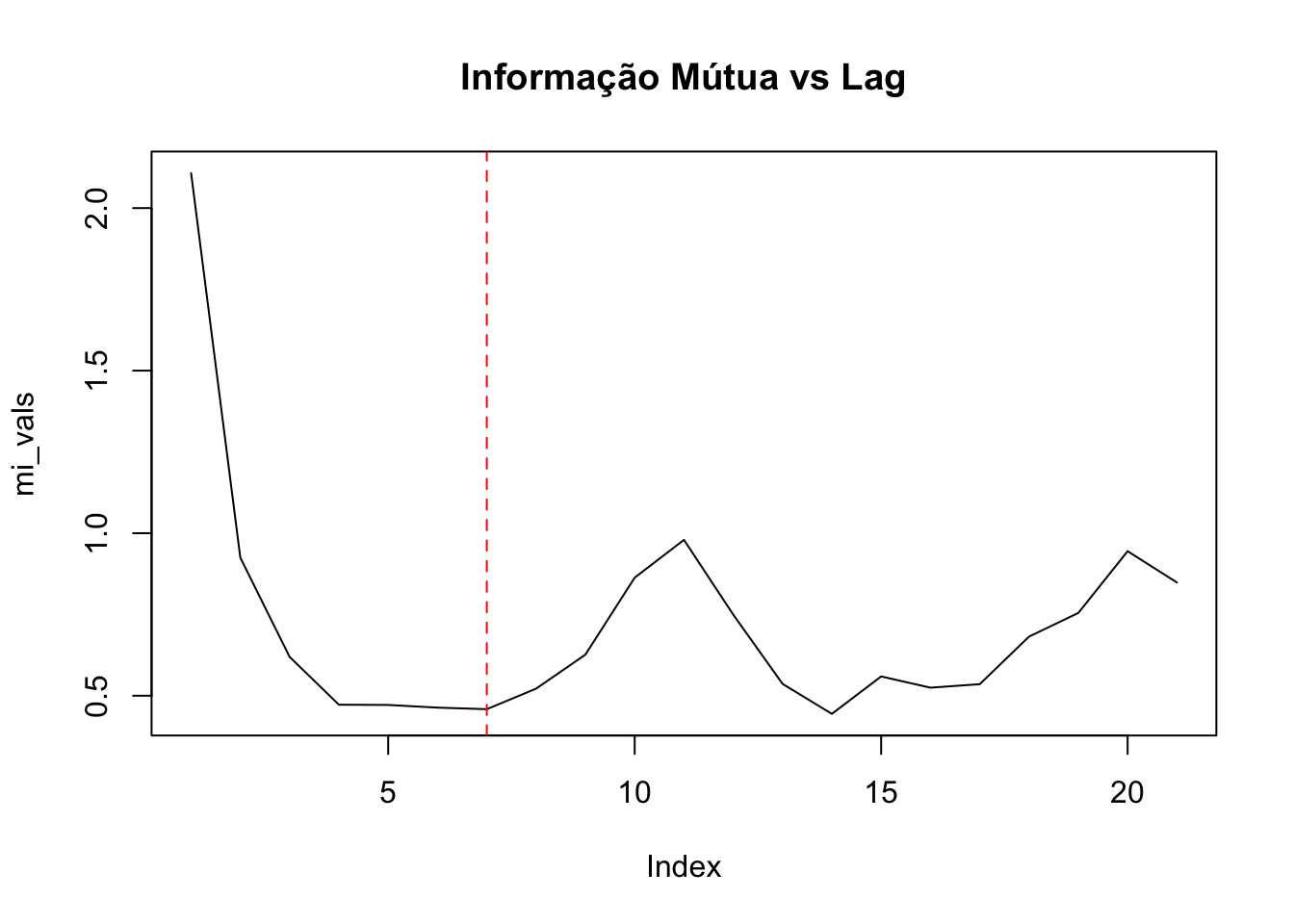
Exemplo 11.59 Encontrando \(d\) e \(m\) ótimos.

# libs
library(tseriesChaos)
library(tsDyn)

# dados
data(lynx)

# Passo 1: Encontra d usando informações mútuas
mi_result <- mutual(lynx, lag.max = 20)

mi_vals <- as.numeric(mi_result)
plot(mi_vals, type = "l", main = "Informação Mútua vs Lag")

# Detecção simples do primeiro mínimo
best_d <- which.min(mi_vals[1:10])  # Olha nos primeiros 10 lags
abline(v = best_d, col = "red", lty = 2)

# Passo 2: testar o desempenho da previsão com diferentes valores de m
best_rmse <- Inf
best_m <- 2

# Usa os últimos 10 pontos para testar a previsão
test_size <- 10
train_data <- lynx[1:(length(lynx)-test_size)]

for(i in 2:6) {
  tryCatch({
    # Ajuste do modelo SETAR (não linear)
    model <- setar(train_data, m = i, d = best_d)
    
    # Prever os próximos valores
    predictions <- predict(model, n.ahead = test_size)
    
    # Calcular RMSE no conjunto de teste
    actual <- lynx[(length(lynx)-test_size+1):length(lynx)]
    rmse <- sqrt(mean((predictions - actual)^2, na.rm = TRUE))
    
    cat("m =", i, "RMSE =", rmse, "\n")
    
    if(rmse < best_rmse) {
      best_rmse <- rmse
      best_m <- i
    }
  }, error = function(e) {
    cat("Modelo falhou para m =", i, "\n")
  })
}
## m = 2 RMSE = 1359.775
## m = 3 RMSE = 2066.418
## m = 4 RMSE = 2302.059
## m = 5 RMSE = 2337.257
## m = 6 RMSE = 3510.999
cat("\nParâmetros recomendados: m =", best_m, ", d =", best_d, "\n")
## 
## Parâmetros recomendados: m = 2 , d = 7

O método para estimar \(m\) e \(d\) é chamado time-delay embedding, e está baseado no Teorema de Token (Takens 2002). Token demonstra ser possível reconstruir um sistema complexo de espaços de estados usando cópias com defasagem de tempo de uma única variável observada. Para mais detalhes veja (Fraser and Swinney 1986) e (Hegger, Kantz, and Schreiber 1999).

11.13.1.3 Teste BDS

It is well known that processes which are linearly independent, i.e. with zero autocorrelations at all lags, can exhibit higher order dependence or nonlinear dependence. (Manzan 2003, 17)

O teste de não linearidade BDS foi desenvolvido por William Brock, W. Davis Dechert e José Alexandre Scheinkman em 1987, publicado posteriormente por (Brock et al. 1996). A proposta é calcular a estatística de teste BDS sob a hipótese nula de que a série temporal testada é uma sequência de variáveis aleatórias iid.

O teste está implementado na função fNonlinear::bdsTest() (Wuertz, Setz, and Chalabi 2024).

Exemplo 11.60 Adapatado de (Tsay and Chen 2019, 20–24) e da documentação de fNonlinear::bdsTest().

library(fNonlinear)
set.seed(1); fNonlinear::bdsTest(rnorm(length(lynx))) # ruído branco gaussiano
## 
## Title:
##  BDS Test
## 
## Test Results:
##   PARAMETER:
##     Max Embedding Dimension: 3
##     eps[1]: 0.45
##     eps[2]: 0.9
##     eps[3]: 1.35
##     eps[4]: 1.8
##   STATISTIC:
##     eps[1] m=2: -1.1487
##     eps[1] m=3: -3.1486
##     eps[2] m=2: -2.1158
##     eps[2] m=3: -2.3245
##     eps[3] m=2: -2.2512
##     eps[3] m=3: -2.4027
##     eps[4] m=2: -2.1239
##     eps[4] m=3: -2.1362
##   P VALUE:
##     eps[1] m=2: 0.2507 
##     eps[1] m=3: 0.001641 
##     eps[2] m=2: 0.03436 
##     eps[2] m=3: 0.0201 
##     eps[3] m=2: 0.02437 
##     eps[3] m=3: 0.01627 
##     eps[4] m=2: 0.03368 
##     eps[4] m=3: 0.03266 
## 
## Description:
##  Thu Oct  9 20:06:10 2025 by user:
fNonlinear::bdsTest(log10(lynx))
## 
## Title:
##  BDS Test
## 
## Test Results:
##   PARAMETER:
##     Max Embedding Dimension: 3
##     eps[1]: 0.279
##     eps[2]: 0.558
##     eps[3]: 0.838
##     eps[4]: 1.117
##   STATISTIC:
##     eps[1] m=2: 51.4822
##     eps[1] m=3: 82.9787
##     eps[2] m=2: 32.0318
##     eps[2] m=3: 38.6321
##     eps[3] m=2: 20.7438
##     eps[3] m=3: 19.3338
##     eps[4] m=2: 16.4341
##     eps[4] m=3: 14.3115
##   P VALUE:
##     eps[1] m=2: < 2.2e-16 
##     eps[1] m=3: < 2.2e-16 
##     eps[2] m=2: < 2.2e-16 
##     eps[2] m=3: < 2.2e-16 
##     eps[3] m=2: < 2.2e-16 
##     eps[3] m=3: < 2.2e-16 
##     eps[4] m=2: < 2.2e-16 
##     eps[4] m=3: < 2.2e-16 
## 
## Description:
##  Thu Oct  9 20:06:10 2025 by user:

O teste BDS também está implementado na função tseries::bds.test() (Trapletti and Hornik 2024).

library(tseries)
set.seed(1); tseries::bds.test(rnorm(length(lynx))) # ruído branco gaussiano
## 
##   BDS Test 
## 
## data:  rnorm(length(lynx)) 
## 
## Embedding dimension =  2 3 
## 
## Epsilon for close points =  0.45 0.90 1.35 1.80 
## 
## Standard Normal = 
##       [ 0.45 ] [ 0.9 ] [ 1.35 ] [ 1.8 ]
## [ 2 ]  -1.1487 -2.1158  -2.2512 -2.1239
## [ 3 ]  -3.1486 -2.3245  -2.4027 -2.1362
## 
## p-value = 
##       [ 0.45 ] [ 0.9 ] [ 1.35 ] [ 1.8 ]
## [ 2 ]   0.2507  0.0344   0.0244  0.0337
## [ 3 ]   0.0016  0.0201   0.0163  0.0327
tseries::bds.test(log10(lynx))
## 
##   BDS Test 
## 
## data:  log10(lynx) 
## 
## Embedding dimension =  2 3 
## 
## Epsilon for close points =  0.2792 0.5584 0.8376 1.1168 
## 
## Standard Normal = 
##       [ 0.2792 ] [ 0.5584 ] [ 0.8376 ] [ 1.1168 ]
## [ 2 ]    51.4822    32.0318    20.7438    16.4341
## [ 3 ]    82.9787    38.6321    19.3338    14.3115
## 
## p-value = 
##       [ 0.2792 ] [ 0.5584 ] [ 0.8376 ] [ 1.1168 ]
## [ 2 ]          0          0          0          0
## [ 3 ]          0          0          0          0

11.13.2 Modelo autorregressivo não linear

Seja o processo estocástico a tempo discreto \(Y_t\) gerado pelo mapeamento \[\begin{equation} Y_{t+s} = f(Y_t,Y_{t-d},\ldots,Y_{t-(m-1)d}|\theta) + a_{t+s} \tag{11.45} \end{equation}\] onde \(a_t \sim WN(0,\sigma_a)\), \(a_{t+s} \perp\!\!\!\perp Y_{t+s}\) e \(f\) é uma função genérica de \(\mathcal{R}^m\) em \(\mathcal{R}\). Esta classe de modelos é frequentemente referenciada na literatura com a sigla NLAR\((m)\), que significa Não Linear AutoRegressivo de ordem \(m\).

A dimensão de incorporação \(m\) em séries temporais é o comprimento do vetor usado para reconstruir o espaço de estados (ou espaço de fase) sucessivo de um processo, que mostra as características dinâmicas de uma série temporal. Conforme (Tsay and Chen 2019, 22), considerando \(m\) um inteiro positivo define-se uma \(m\)-história (\(m\)-history) de uma série temporal como \[\begin{equation} \boldsymbol{y}_t^m = (y_t, y_{t−1}, \ldots, y_{t−m+1}) \text{ para } t = m, \ldots, T. \tag{11.45} \end{equation}\]

A função tsDyn::availableModels() retorna a lista de modelos de séries temporais da classe nlar disponíveis.

tsDyn::availableModels()
##  [1] "linear"  "nnetTs"  "setar"   "lstar"   "star"    "aar"     "lineVar" "VECM"    "TVAR"    "TVECM"
Modelo Equação
linear \[Y_{t+s} = \phi + \phi_0 Y_t + \phi_1 Y_{t-d} + \ldots + \phi_m Y_{t-(m-1)d} + a_{t+s}\]
nnetTs \[Y_{t+s} = \beta_0 + \sum_{j=1}^{D} \beta_j g(\gamma_{0j} + \sum_{i=1}^{m} \gamma_{ij} Y_{t-(i-1)d})\]
setar \[Y_{t+s} = \left\{ \begin{array}{l l} \phi_1 + \phi_{10}Y_t + \phi_{11}Y_{t-d} + \ldots + \phi_{1L}Y_{t-(L-1)d} + a_{t+s}, & \quad Z_t \le th\\ \phi_2 + \phi_{20}Y_t + \phi_{21}Y_{t-d} + \ldots + \phi_{2H}Y_{t-(H-1)d} + a_{t+s}, & \quad Z_t < th\\ \end{array} \right.\]
lstar \[Y_{t+s} = (\phi_1 + \phi_{10}Y_t + \phi_{11}Y_{t-d} + \ldots + \phi_{1L}Y_{t-(L-1)d})(1-G(Z_t,\gamma,th)) + (\phi_2 + \phi_{20}Y_t + \phi_{21}Y_{t-d} + \ldots + \phi_{2H}Y_{t-(H-1)d})G(Z_t,\gamma,th) + a_{t+s}\]
star
aar \[Y_{t+s} = \mu + \sum_{i=1}^{m} s_i(Y_{t-(i-1)d})\]
lineVar
VECM
TVAR
TVECM
  • \(m\): dimensão de incorporação (embedding dimension), AR\((p-1)\)?
  • \(d\): atraso de tempo (time delay), equivale à diferença sazonal \(D\)?
  • \(s\): passos de previsão (forecasting steps)
  • \(Z_t\): variável limite (threshold variable)
  • \(th\): limite (threshold)
  • \(D\): unidades ocultas (hidden units)
  • \(g\): função de ativação (activation function)
  • \(G\): função logística (logistic function)
  • \(\delta\): limite de atraso (threshold delay)

11.13.3 Rede neural autorregressiva

De acordo com (Rob J. Hyndman and Athanasopoulos 2021), a função forecast::nnetar() ajusta um modelo NNAR\((p,P,k)_m\), que é análogo a um modelo ARIMA\((p,0,0)(P,0,0)_m\) com funções não lineares, onde \(k\) é o número de nós ocultos. Segundo a documentação, o argumento xreg permite a entrada de covariáveis, omitindo-se as linhas correspondentes a y e xreg se houver valores ausentes. A rede é treinada para previsão de uma etapa, e previsões de várias etapas são calculadas recursivamente.

Se os valores de \(p\) e \(P\) não forem especificados, eles serão selecionados automaticamente. Para séries temporais não sazonais, o padrão é o número ótimo de defasagens de acordo com o AIC para um modelo AR\((p)\) linear. Para séries temporais sazonais, os valores padrão são \(P=1\) e \(p\) é escolhido do modelo linear ótimo ajustado aos dados ajustados sazonalmente. Se \(k\) não for especificado, ele será definido como \(k=(p+P+1)/2\) arredondado para o inteiro mais próximo.

Exemplos, sendo que os modelos de rede neural não possuem as restrições nos parâmetros para garantir a estacionariedade.

  • NNAR\((p,0) \equiv\) ARIMA\((p,0,0)\)
  • NNAR\((p,P,0)_m \equiv\) ARIMA\((p,0,0)(P,0,0)_m\)

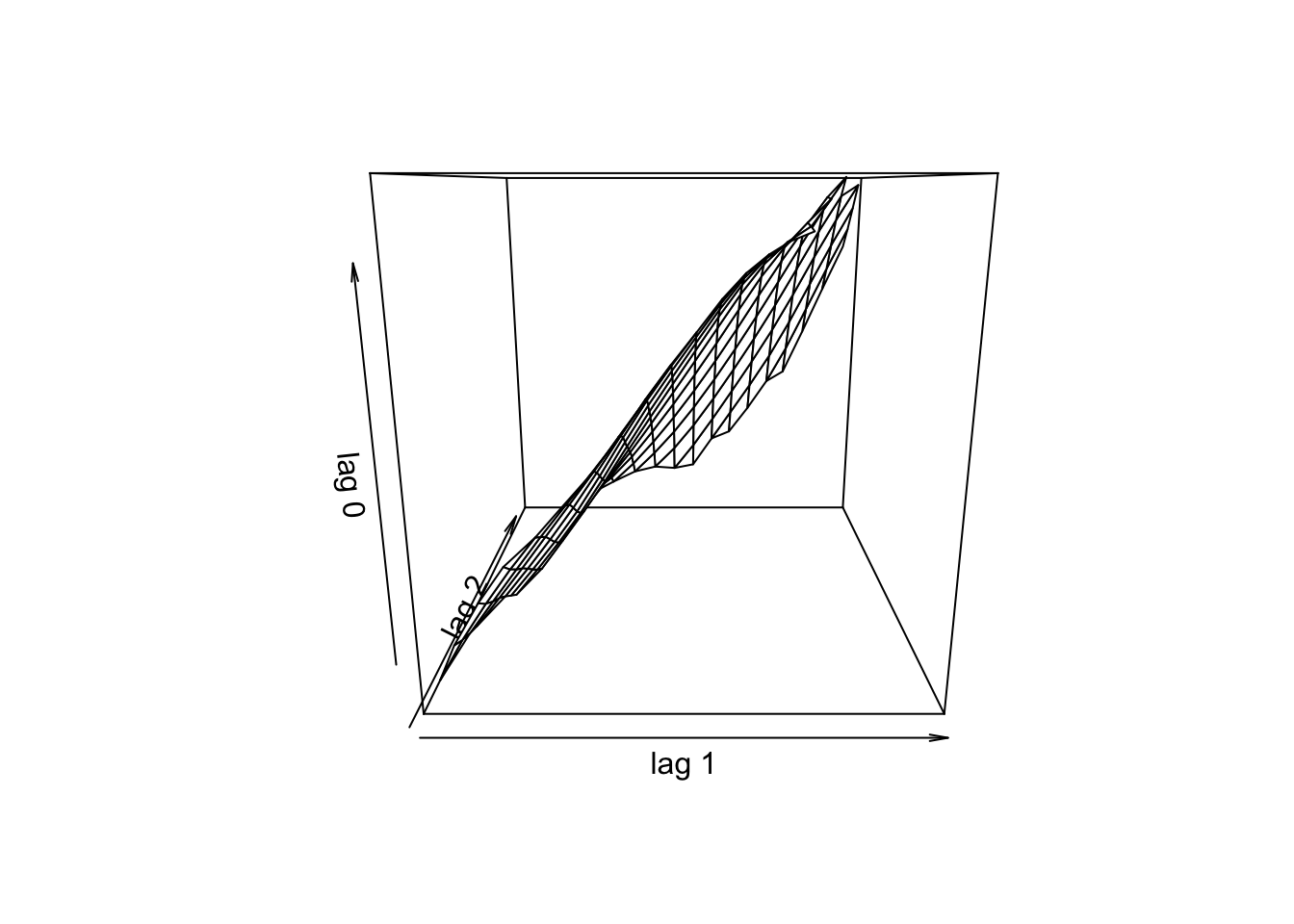
Exemplo 11.61 Aplicação de forecast::nnetar() na série temporal datasets::lynx.

library(forecast)
fit <- forecast::nnetar(lynx)
plot(predict(fit, h = 24))

Pode-se usar a estratégia treino-teste e calcular métricas de desempenho de previsão.

library(forecast)
fit <- forecast::nnetar(window(lynx, end=1913))
plot(predict(fit, h=24))
lines(lynx)

forecast::accuracy(fit)
##                     ME     RMSE      MAE       MPE     MAPE      MASE       ACF1
## Training set 0.1280635 278.9293 186.8424 -32.64067 44.75747 0.2174152 -0.1422465

Exercício 11.34

  1. Teste plot(predict(fit, h = 48, PI = TRUE)).
  2. Veja https://otexts.com/fpp3/nnetar.html

11.13.4 LSTM (Long Short-Term Memory)

O modelo LSTM (Long Short-Term Memory) é uma arquitetura baseada em Rede Neural Recorrente (RNN) utilizada para previsão de séries temporais. Será considera a abordagem da biblioteca TSLSTM (Dr. R. K. Paul and Yeasin 2022), que utiliza os módulos Keras e TensorFlow (R. K. Paul and Garai 2021).

Exemplo 11.62 Adaptado da documentação de TSLSTMplus::ts.lstm().

library(TSLSTMplus)
fit_lstm <- TSLSTMplus::ts.lstm(ts = lynx, tsLag = 2,
                                LSTMUnits = 5, Epochs = 2)
## Model: "sequential"
## __________________________________________________________________________________________________________________
##  Layer (type)                                      Output Shape                                 Param #           
## ==================================================================================================================
##  lstm (LSTM)                                       (1, 5)                                       140               
##  dense (Dense)                                     (1, 1)                                       6                 
## ==================================================================================================================
## Total params: 146 (584.00 Byte)
## Trainable params: 146 (584.00 Byte)
## Non-trainable params: 0 (0.00 Byte)
## __________________________________________________________________________________________________________________
## Epoch 1/2
## 100/100 - 7s - loss: 1.1355 - mae: 0.8550 - val_loss: 0.5138 - val_mae: 0.5992 - 7s/epoch - 72ms/step
## Epoch 2/2
## 100/100 - 0s - loss: 1.0467 - mae: 0.8160 - val_loss: 0.4872 - val_mae: 0.5837 - 223ms/epoch - 2ms/step
                                # Optimizer = 'tf.keras.optimizers.legacy.RMSprop')
current_values <- stats::predict(fit_lstm, ts = lynx)
## 4/4 - 0s - 257ms/epoch - 64ms/step
future_values <- predict(fit_lstm, horizon = 24, ts = lynx)
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 8ms/epoch - 8ms/step
## 1/1 - 0s - 9ms/epoch - 9ms/step

Exercício 11.35 Veja

  1. ?TSLSTMplus::ts.lstm.
  2. https://stackoverflow.com/questions/77222463/is-there-a-way-to-change-adam-to-legacy-when-using-mac-m1-m2-in-tensorflow
  3. WARNING:absl:At this time, the v2.11+ optimizer tf.keras.optimizers.RMSprop runs slowly on M1/M2 Macs, please use the legacy Keras optimizer instead, located at tf.keras.optimizers.legacy.RMSprop.

11.13.5 GLARMA

(Dunsmuir and Scott 2015) apresentam o pacote glarma (Generalized Linear AutoRegressive Moving Average), que traz funções “para estimativa, teste, verificação de diagnóstico e previsão de modelos de média móvel autorregressiva linear generalizada (GLARMA) para séries temporais de valores discretos com variáveis de regressão”, sendo “uma classe de modelos de espaço de estado não lineares não gaussianos”. Ainda segundo a documentação, “[o] vetor de estado consiste em um componente de regressão linear mais um componente orientado por observação que consiste em um filtro de média móvel autorregressiva (ARMA) de resíduos preditivos anteriores”. Atualmente conta com as distribuições Poisson, binomial negativa e binomial para modelar a série da variável resposta, e “[t]rês opções (Pearson, tipo pontuação e não escalonada) para os resíduos no componente”. “Os testes de razão de verossimilhança e Wald para o componente orientado por observação permitem testar a dependência serial em configurações de modelo linear generalizado”, incluindo ainda “[d]iagnósticos gráficos, incluindo ajustes de modelo, funções de autocorrelação e resíduos de transformação integral de probabilidade”.

library(glarma)

Exercício 11.36 Veja

  1. Vinheta de glarma

References

Brock, William A, José Alexandre Scheinkman, W Davis Dechert, and Blake LeBaron. 1996. “A Test for Independence Based on the Correlation Dimension.” Econometric Reviews 15 (3): 197–235. https://d1wqtxts1xzle7.cloudfront.net/51470360/bdsl-libre.pdf?1485122147=&response-content-disposition=inline%3B+filename%3DA_test_for_independence_based_on_the_cor.pdf&Expires=1728987686&Signature=AqWbxMKbM2m3f6AI1rwvxVN5coSSy-RA1RhAiBIdfkNOHqOb4gyC44rjZCmKzcroVdvUhSLqH8uhlDuA01TIypBs9R~g5AHPWtt4JquQP2WYOirMMsi9pKqDirfRsq0YrR6PFJwtBJOjHrLYEx~rjv391F4~kLcUL0KcrF3WNoGqmoUu9IGV1uJANPRncuvGz2wTIeiD86jI8tNXGik3eGhhCxmbHLpKTCPT62oHyOMovfgVO8wNlg~XUIIAP1EXWaEZROpnGrrkzU6HiBUAS2fjzKSM79KpaLioxsBH~vXVpDkJEEQaDA5dzizLdMNJm2DoeUbNVnxyuu6tYXaNWw__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA.
Casdagli, Martin. 1992. “Chaos and Deterministic Versus Stochastic Non-Linear Modelling.” Journal of the Royal Statistical Society: Series B (Methodological) 54 (2): 303–28. https://sfi-edu.s3.amazonaws.com/sfi-edu/production/uploads/sfi-com/dev/uploads/filer/0c/a9/0ca97a96-090c-4eac-ba4e-0bd03f130ac4/91-07-029.pdf.
Dunsmuir, William T. M., and David J. Scott. 2015. “The glarma Package for Observation-Driven Time Series Regression of Counts.” Journal of Statistical Software 67 (7): 1–36. https://doi.org/10.18637/jss.v067.i07.
Fabio Di Narzo, Antonio, Jose Luis Aznarte, and Matthieu Stigler. 2024. tsDyn: Time Series Analysis Based on Dynamical Systems Theory.
Fraser, Andrew M, and Harry L Swinney. 1986. “Independent Coordinates for Strange Attractors from Mutual Information.” Physical Review A 33 (2): 1134. https://journals.aps.org/pra/pdf/10.1103/PhysRevA.33.1134?casa_token=ZoqRPZ-mVJYAAAAA%3A1FH2CeFnsBBatvQu3ICtHAMLIV9fuV6Qiwzi1YVPF35mK03On1y2aUjwGo3FvkbKTlyG4hjW84P7iKE.
Hegger, Rainer, Holger Kantz, and Thomas Schreiber. 1999. “Practical Implementation of Nonlinear Time Series Methods: The <Scp>TISEAN</Scp> Package.” Chaos: An Interdisciplinary Journal of Nonlinear Science 9 (2): 413–35. https://doi.org/10.1063/1.166424.
———. 2021. Forecasting: Principles and Practice, 3rd Ed. OTexts. https://otexts.com/fpp3/.
Manzan, Sebastiano. 2003. Essays in Nonlinear Economic Dynamics. Thela Thesis, Amsterdam. https://hdl.handle.net/11245/1.219285.
Paul, Dr. Ranjit Kumar, and Dr. Md Yeasin. 2022. TSLSTM: Long Short Term Memory (LSTM) Model for Time Series Forecasting. https://CRAN.R-project.org/package=TSLSTM.
Paul, Ranjit Kumar, and Sandip Garai. 2021. “Performance Comparison of Wavelets-Based Machine Learning Technique for Forecasting Agricultural Commodity Prices.” Soft Computing 25 (20): 12857–73.
Stigler, Matthieu. 2019. “Nonlinear time series in R: Threshold cointegration with tsDyn.” In Handbook of Statistics, Volume 41, edited by Hrishikesh D. Vinod and C. R. Rao, 42:229–64. Elsevier. https://doi.org/10.1016/bs.host.2019.01.008.
Takens, Floris. 2002. “The Reconstruction Theorem for Endomorphisms (1981).” Bulletin of the Brazilian Mathematical Society 33 (2): 231–62. https://doi.org/10.1007/s005740200012.
Trapletti, Adrian, and Kurt Hornik. 2024. Tseries: Time Series Analysis and Computational Finance. https://CRAN.R-project.org/package=tseries.
Tsay, Ruey S., and Rong Chen. 2019. Nonlinear Time Series Analysis. John Wiley & Sons.
Wuertz, Diethelm, Tobias Setz, and Yohan Chalabi. 2024. fNonlinear: Rmetrics - Nonlinear and Chaotic Time Series Modelling. https://CRAN.R-project.org/package=fNonlinear.