11.15 Vetor autorregressivo (VAR)

A abordagem será baseada na biblioteca MTS (Tsay, Wood, and Lachmann 2022) e em (Tsay 2014).

Exercício 11.41 Veja

  1. https://cran.r-universe.dev/MTS/doc/manual.html
  2. https://matzc.github.io/tmseries/lecture11.html
  3. http://past.rinfinance.com/agenda/2013/talk/RueyTsay.pdf

11.15.1 Covariância e correlação cruzadas

De acordo com (Diggle 1990, 202–3), a função de covariância cruzada de um processo aleatório estacionário bivariado \(\{(X_t,Y_t)\}\) é o conjunto de números \(\gamma_{xy}(k)\) definido, para cada inteiro \(k\), por \[\begin{equation} \gamma_{xy}(k) = cov(X_{t},Y_{t-k}) \tag{11.55} \end{equation}\]

Note que \(\gamma_{xx}(k)\) e \(\gamma_{yy}(k)\) são as funções de autocovariância de \(\{X_t\}\) e \(\{Y_t\}\) respectivamente, conforme Eq. (11.7). Da mesma forma, \[\gamma_{xy}(-k) = cov(X_t,Y_{t+k}) \\ \hspace{34pt} = cov(Y_{t+k},X_t) \\ \hspace{74pt} = cov(Y_t,X_{t-k}) = \gamma_{yx}(k)\]

A função de correlação cruzada de \(\{(X_t,Y_t)\}\) é \[\begin{equation} \rho_{xy}(k) = \frac{\gamma_{xy}(k)}{\sqrt{\gamma_{xx}(0) \gamma_{yy}(0)}} \tag{11.56} \end{equation}\]

O estimador da função de correlação cruzada é o correlograma cruzado tal que \[\begin{equation} \hat{\rho}_{xy}(k) = \frac{\hat{\gamma}_{xy}(k)}{\sqrt{\hat{\gamma}_{xx}(0) \hat{\gamma}_{yy}(0)}} \tag{11.57} \end{equation}\] onde \[\hat{\gamma}_{xx}(0) = \frac{1}{n} \sum_{t=1}^{n} (x_t-\bar{x})^2, \;\;\;\;\; \hat{\gamma}_{yy}(0) = \frac{1}{n} \sum_{t=1}^{n} (y_t-\bar{y})^2,\] \[\bar{x} = \frac{1}{n} \sum_{t=1}^{n} x_t, \;\;\;\;\; \bar{y} = \frac{1}{n} \sum_{t=1}^{n} y_t,\] \[\hat{\gamma}_{xy}(k) = \left\{ \begin{array}{l l} n^{-1} \sum_{t=k+1}^{n} (x_{t}-\bar{x}) (x_{t-k}-\bar{y}), & \quad k \ge 0\\ n^{-1} \sum_{t=1}^{n+k} (x_{t}-\bar{x}) (x_{t-k}-\bar{y}), & \quad k < 0\\ \end{array} \right. \]

A função stats::ccf calcula as estimativas da correlação cruzada e da covariância cruzada de duas séries univariadas.

Exemplo 11.64 Considere duas séries temporais simladas de ruído branco gaussiano.

set.seed(42)
zt <- matrix(rnorm(200), ncol = 2)
colnames(zt) <- c('z1','z2')
# covariância cruzada
stats::ccf(zt[,'z1'], zt[,'z2'], type = 'covariance',
           ylab = 'cross-covariance', main = 'stats::ccf(type = "covariance")')

# correlação cruzada
stats::ccf(zt[,'z1'], zt[,'z2'],
           ylab = 'cross-correlation', main = 'stats::ccf(type = "correlation")')

Exemplo 11.65 Considere as séries temporais que das mortes mensais por bronquite, enfisema e asma no Reino Unido entre 1974–1979, ambos os sexos (ldeaths), homens (mdeaths) e mulheres (fdeaths), apresentada por (Diggle 1990, 238).

# correlação cruzada
stats::ccf(mdeaths, fdeaths,
           ylab = 'cross-correlation', main = 'stats::ccf(type = "correlation")')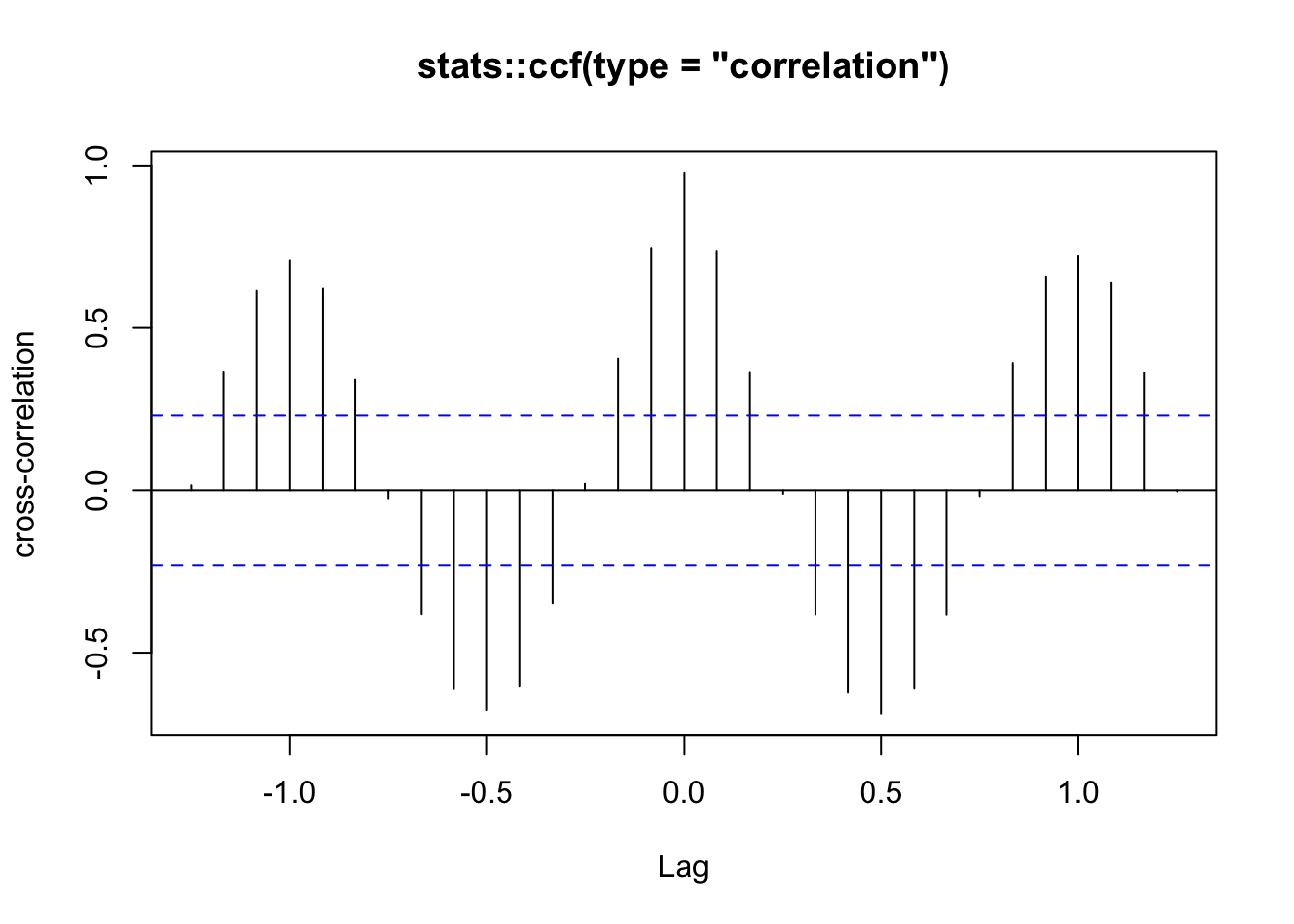

11.15.2 Teste de causalidade de Granger

[U]nder Granger’s framework, we say that \(z_{1t}\) causes \(z_{2t}\) if the past information of \(z_{1t}\) improves the forecast of \(z_{2t}\). (Tsay 2014, 29)

(Granger 1969) propõe o teste de causalidade de Granger, que na verdade testa se uma série \(z_{1t}\) é capaz de prever uma série \(z_{2t}\).

Exemplo 11.66 Baseado na documentação de MTS::GrangerTest().

library(MTS)
set.seed(42)
zt <- matrix(rnorm(200), ncol = 2)
colnames(zt) <- c('z1','z2')
# teste de Granger
MTS::GrangerTest(zt, p = 1)
## Number of targeted zero parameters:  1 
## Chi-square test for Granger Causality and p-value:  2.251435 0.1334906 
## Constant term: 
## Estimates:  0.01752419 -0.1075215 
## Std.Error:  0.1047053 0.0906709 
## AR coefficient matrix 
## AR( 1 )-matrix 
##         [,1]   [,2]
## [1,]  0.0560  0.000
## [2,] -0.0955 -0.106
## standard error 
##        [,1]   [,2]
## [1,] 0.1007 0.0000
## [2,] 0.0868 0.0998
##   
## Residuals cov-mtx: 
##             [,1]        [,2]
## [1,] 1.062752024 0.002823729
## [2,] 0.002823729 0.780929140
##   
## det(SSE) =  0.8299261 
## AIC =  -0.1264187 
## BIC =  -0.04826357 
## HQ  =  -0.0947879
MTS::GrangerTest(zt, p = 2)
## Number of targeted zero parameters:  2 
## Chi-square test for Granger Causality and p-value:  3.387032 0.1838719 
## Constant term: 
## Estimates:  0.02434786 -0.129605 
## Std.Error:  0.106115 0.09188827 
## AR coefficient matrix 
## AR( 1 )-matrix 
##        [,1]   [,2]
## [1,]  0.065  0.000
## [2,] -0.123 -0.124
## standard error 
##        [,1]  [,2]
## [1,] 0.1026 0.000
## [2,] 0.0887 0.102
## AR( 2 )-matrix 
##          [,1]    [,2]
## [1,] -0.00821  0.0000
## [2,]  0.07395 -0.0396
## standard error 
##        [,1]  [,2]
## [1,] 0.1017 0.000
## [2,] 0.0873 0.104
##   
## Residuals cov-mtx: 
##           [,1]      [,2]
## [1,] 1.0689678 0.0156749
## [2,] 0.0156749 0.7606777
##   
## det(SSE) =  0.8128942 
## AIC =  -0.08715432 
## BIC =  0.06915589 
## HQ  =  -0.02389276
MTS::GrangerTest(zt, p = 3)
## Number of targeted zero parameters:  3 
## Chi-square test for Granger Causality and p-value:  7.073532 0.06959063 
## Constant term: 
## Estimates:  0.01888439 -0.1239715 
## Std.Error:  0.1077134 0.09462076 
## AR coefficient matrix 
## AR( 1 )-matrix 
##         [,1]   [,2]
## [1,]  0.0675  0.000
## [2,] -0.1233 -0.116
## standard error 
##        [,1]  [,2]
## [1,] 0.1037 0.000
## [2,] 0.0899 0.105
## AR( 2 )-matrix 
##         [,1]    [,2]
## [1,] -0.0155  0.0000
## [2,]  0.0772 -0.0198
## standard error 
##        [,1]  [,2]
## [1,] 0.1037 0.000
## [2,] 0.0907 0.107
## AR( 3 )-matrix 
##        [,1]    [,2]
## [1,] 0.0370  0.0000
## [2,] 0.0753 -0.0299
## standard error 
##       [,1]  [,2]
## [1,] 0.104 0.000
## [2,] 0.089 0.106
##   
## Residuals cov-mtx: 
##            [,1]       [,2]
## [1,] 1.07692343 0.01998993
## [2,] 0.01998993 0.75362985
##   
## det(SSE) =  0.811202 
## AIC =  -0.02923812 
## BIC =  0.2052272 
## HQ  =  0.06565421

Exemplo 11.67 (Thurman, Fisher, et al. 1988) examinam séries temporais anuais dos EUA de 1930 a 1983 sobre produção de ovos e população de galinhas. O objetivo é responder à célebre pergunta: quem veio primeiro, o ovo ou a galinha? (Zeileis and Hothorn 2002) apresentam a série temporal ChickEgg, contendo o conjunto de dados fornecido por Walter Thurman e disponibilizado para R por Roger Koenker, sendo os dados ligeiramente diferentes daqueles analisados em (Thurman, Fisher, et al. 1988). As colunas são

  • chicken: número de galinhas (população de 1º de dezembro de todas as galinhas dos EUA, excluindo frangos de corte comerciais)
  • egg: número de ovos (produção de ovos nos EUA em milhões de dúzias)
library(lmtest)
plot(ChickEgg)

# galinhas granger-causam ovos?
ec1 <- grangertest(egg ~ chicken, order = 1, data = ChickEgg)
ec2 <- grangertest(egg ~ chicken, order = 2, data = ChickEgg)
ec3 <- grangertest(egg ~ chicken, order = 3, data = ChickEgg)
ec4 <- grangertest(egg ~ chicken, order = 4, data = ChickEgg)
ec5 <- grangertest(egg ~ chicken, order = 5, data = ChickEgg)
ec6 <- grangertest(egg ~ chicken, order = 6, data = ChickEgg)
ec7 <- grangertest(egg ~ chicken, order = 7, data = ChickEgg)
ec8 <- grangertest(egg ~ chicken, order = 8, data = ChickEgg)
ec9 <- grangertest(egg ~ chicken, order = 9, data = ChickEgg)
ec10 <- grangertest(egg ~ chicken, order = 10, data = ChickEgg)
ec11 <- grangertest(egg ~ chicken, order = 11, data = ChickEgg)
ec12 <- grangertest(egg ~ chicken, order = 12, data = ChickEgg)
# ovos granger-causam galinhas?
ce1 <- grangertest(chicken ~ egg, order = 1, data = ChickEgg)
ce2 <- grangertest(chicken ~ egg, order = 2, data = ChickEgg)
ce3 <- grangertest(chicken ~ egg, order = 3, data = ChickEgg)
ce4 <- grangertest(chicken ~ egg, order = 4, data = ChickEgg)
ce5 <- grangertest(chicken ~ egg, order = 5, data = ChickEgg)
ce6 <- grangertest(chicken ~ egg, order = 6, data = ChickEgg)
ce7 <- grangertest(chicken ~ egg, order = 7, data = ChickEgg)
ce8 <- grangertest(chicken ~ egg, order = 8, data = ChickEgg)
ce9 <- grangertest(chicken ~ egg, order = 9, data = ChickEgg)
ce10 <- grangertest(chicken ~ egg, order = 10, data = ChickEgg)
ce11 <- grangertest(chicken ~ egg, order = 11, data = ChickEgg)
ce12 <- grangertest(chicken ~ egg, order = 12, data = ChickEgg)

A tabela a seguir apresenta os p-values dos testes realizados, que conforme apontado por (Thurman, Fisher, et al. 1988, 237), os testes “indicam uma clara rejeição da hipótese de que os ovos não causam a doença de Granger. Eles não fornecem tal rejeição à hipótese de que as galinhas não causam a doença de Granger. Portanto, concluímos que o ovo veio primeiro”.

Ordem Chicken -> Egg Egg -> Chicken
1 0.8292 0.2772
2 0.4215 6^{-4}
3 0.6238 0.003
4 0.8125 0.0057
5 0.9131 0.0019
6 0.8984 0.0064
7 0.7467 0.0028
8 0.7619 0.0028
9 0.82 0.0028
10 0.9438 0.0028
11 0.9137 0.0028
12 0.9107 0.0028

Exemplo 11.68 Baseado nas documentações de MTS::VAR() e MTS::GrangerTest().

library(MTS)
data('mts-examples', package = 'MTS')
gdp <- log(qgdp[,3:5])
zt <- MTS::diffM(gdp)
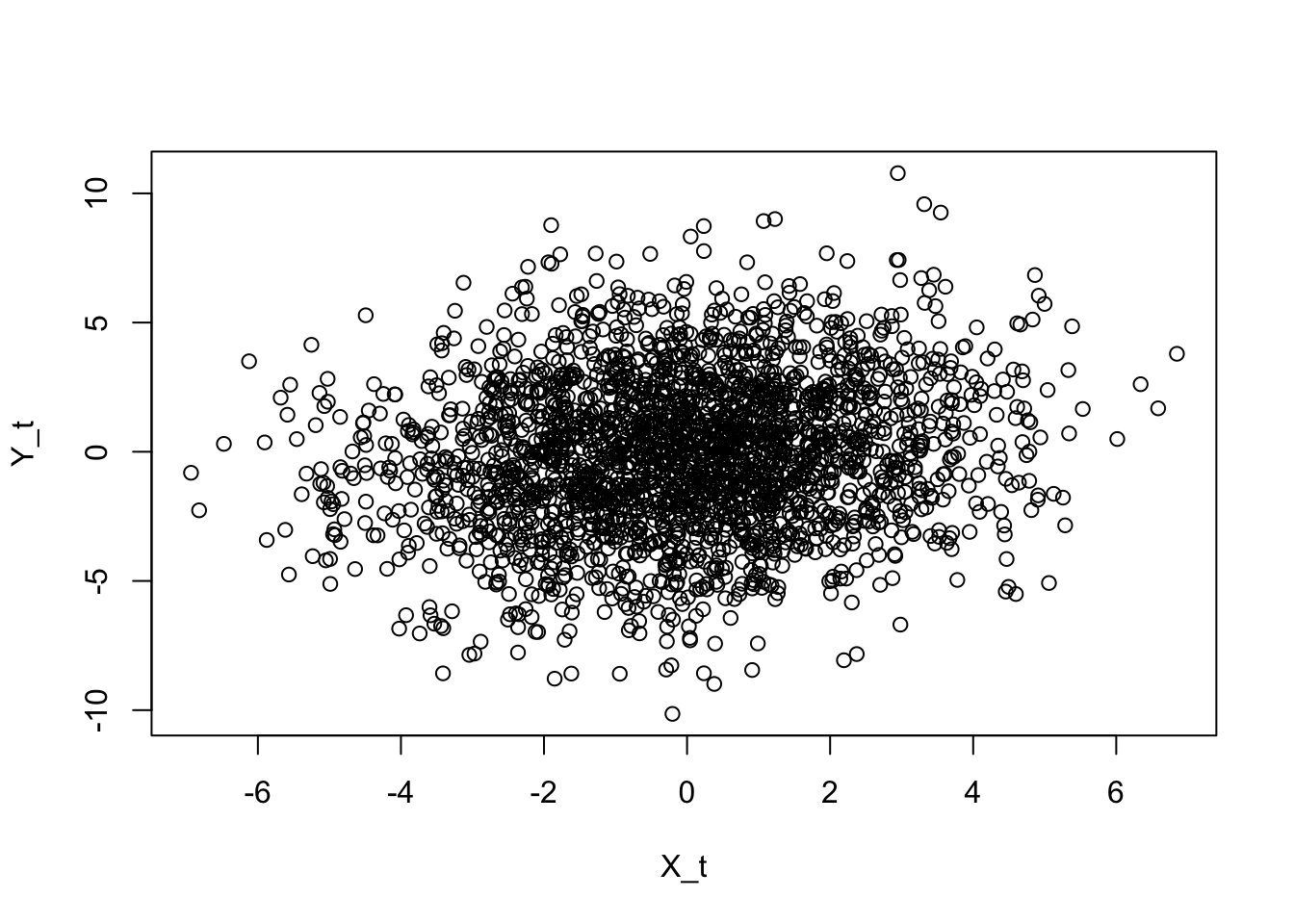
# correlação cruzada
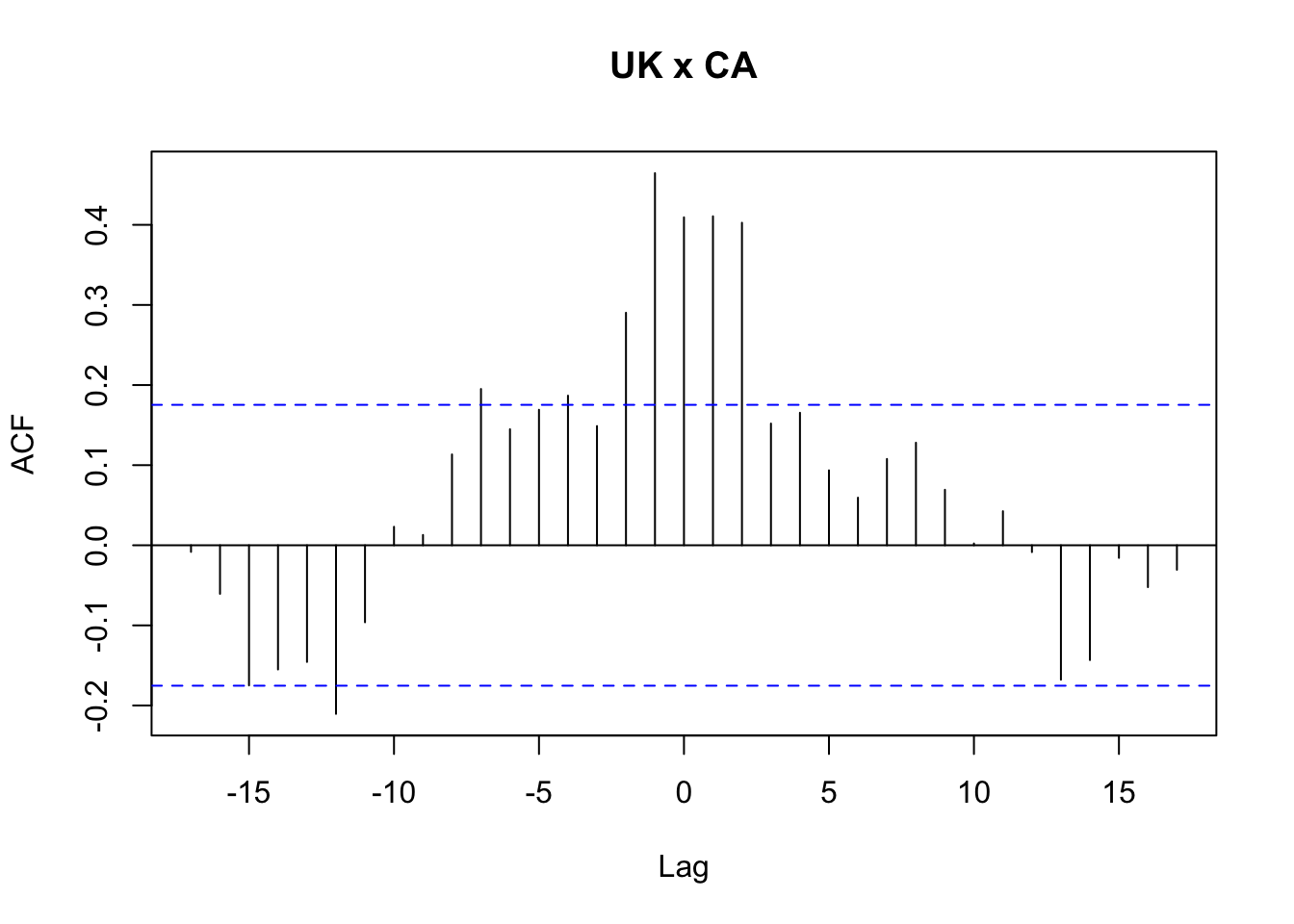
stats::ccf(zt[,'uk'], zt[,'ca'], main = 'UK x CA')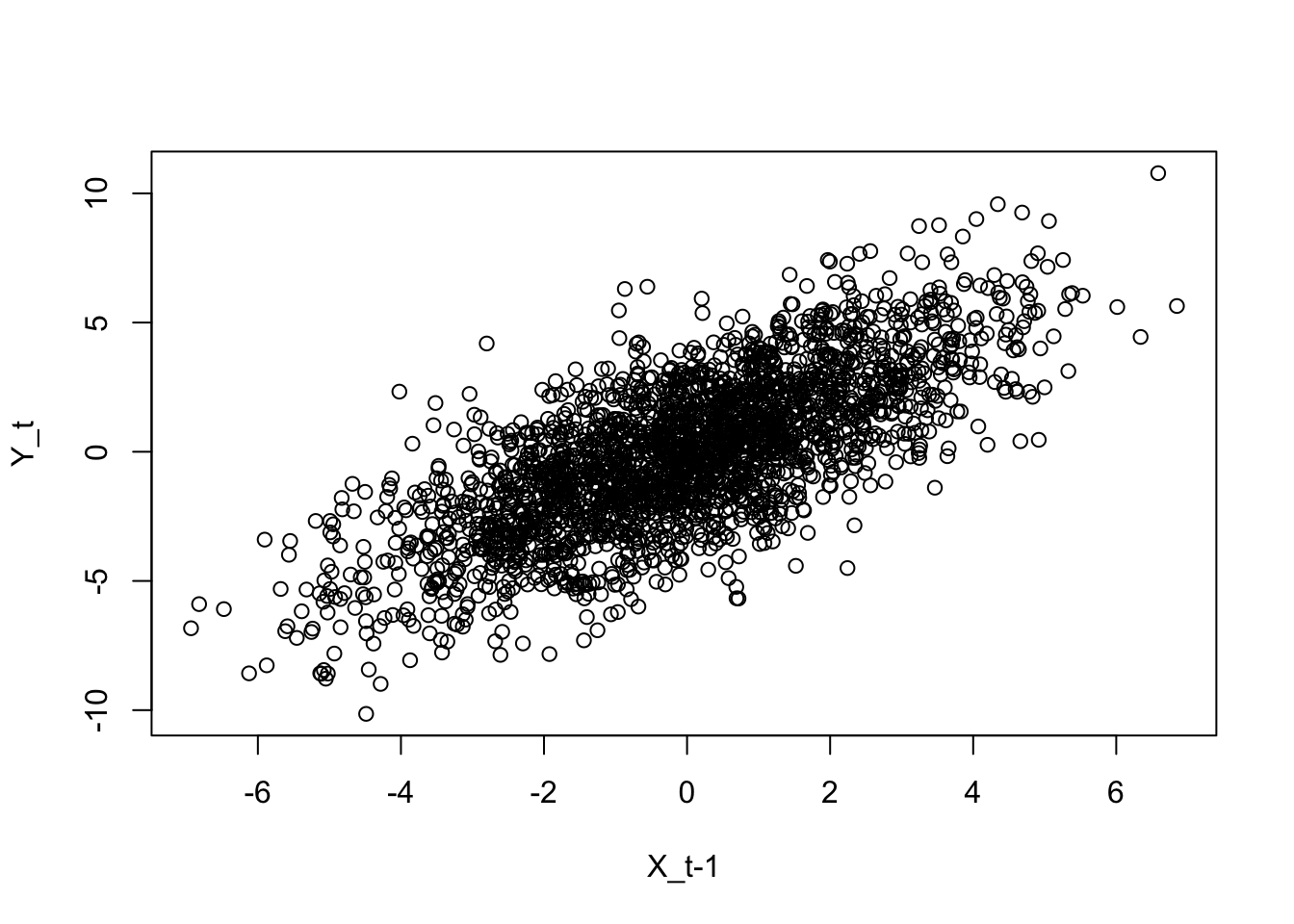

stats::ccf(zt[,'uk'], zt[,'us'], main = 'UK x US')

stats::ccf(zt[,'ca'], zt[,'us'], main = 'CA x US')

# teste de Granger
MTS::GrangerTest(zt, p = 1)
## Number of targeted zero parameters:  2 
## Chi-square test for Granger Causality and p-value:  9.393834 0.00912336
MTS::GrangerTest(zt, p = 2)
## Number of targeted zero parameters:  4 
## Chi-square test for Granger Causality and p-value:  8.948851 0.06239076 
## Constant term: 
## Estimates:  0.002104448 0.001231581 0.002895581 
## Std.Error:  0.0006685632 0.0007382941 0.000816888 
## AR coefficient matrix 
## AR( 1 )-matrix 
##       [,1]  [,2]  [,3]
## [1,] 0.473 0.000 0.000
## [2,] 0.351 0.338 0.469
## [3,] 0.491 0.240 0.236
## standard error 
##        [,1]  [,2]   [,3]
## [1,] 0.0899 0.000 0.0000
## [2,] 0.0949 0.100 0.0926
## [3,] 0.1050 0.111 0.1024
## AR( 2 )-matrix 
##        [,1]   [,2]     [,3]
## [1,]  0.151  0.000  0.00000
## [2,] -0.191 -0.175 -0.00868
## [3,] -0.312 -0.131  0.08531
## standard error 
##        [,1]   [,2]   [,3]
## [1,] 0.0859 0.0000 0.0000
## [2,] 0.0939 0.0890 0.0953
## [3,] 0.1038 0.0984 0.1055
##   
## Residuals cov-mtx: 
##              [,1]         [,2]         [,3]
## [1,] 3.042334e-05 2.654091e-06 7.435286e-06
## [2,] 2.654091e-06 2.915817e-05 1.394879e-05
## [3,] 7.435286e-06 1.394879e-05 3.569657e-05
##   
## det(SSE) =  2.443371e-14 
## AIC =  -31.11881 
## BIC =  -30.80204 
## HQ  =  -30.99013
MTS::GrangerTest(zt, p = 3)
## Number of targeted zero parameters:  6 
## Chi-square test for Granger Causality and p-value:  20.55467 0.002204932

11.15.3 VAR

Conforme (Tsay 2014, 27), a série temporal multivariada \(\boldsymbol{z}_{t}\) segue um modelo VAR de ordem \(p\), VAR\((p)\), se \[\begin{equation} \boldsymbol{z}_{t} = \boldsymbol{\phi}_0 + \sum_{i=1}^{p} \boldsymbol{\phi}_i \boldsymbol{z}_{t-i} + \boldsymbol{a}_{t} \tag{11.58} \end{equation}\] onde \(\boldsymbol{\phi}_0\) é um vetor constante \(k\)-dimensional e \(\boldsymbol{\phi}_i\) são matrizes \(k \times k\) para \(i>0\), \(\boldsymbol{\phi}_p \ne 0\), e \(\boldsymbol{a}_{t}\) é uma sequência de vetores aleatórios independentes e identicamente distribuídos (iid) com média zero e matriz de covariância positiva-definida \(\Sigma_a\).

Com o operador backshift o modelo pode ser expresso por \[\begin{equation} \boldsymbol{\phi}(B)\boldsymbol{z}_{t} = \boldsymbol{\phi}_0 + \boldsymbol{a}_{t} \tag{11.59} \end{equation}\] onde \[\begin{equation} \boldsymbol{\phi}(B) = \boldsymbol{I}_k - \sum_{i=1}^{p} \boldsymbol{\phi}_i B^i \tag{11.60} \end{equation}\] é uma matriz polinomial de grau \(p\).

11.15.3.1 Estacionariedade

  • VAR(1): autovalores absolutos menores que 1 garantem modelo VAR(1) estacionário (Tsay 2014, 31)
  • VAR(2): “the necessary and sufficient condition for the stationarity of \(\boldsymbol{Z}_t\) (…) is that all solutions of the determinant equation \(|\phi(B)| = 0\) are greater than 1 in absolute value.” (Tsay 2014, 38)
  • VAR\((p)\): “the necessary and sufficient condition for the weak stationarity of the VAR\((p)\) series is that all solutions of the determinant equation \(|\phi(B)| = 0\) must be greater than 1 in modulus.” (Tsay 2014, 42)

Exemplo 11.69 Baseado nas documentações de MTS::VAR() e MTS::VARpred().

library(MTS)
data('mts-examples', package = 'MTS')
gdp <- log(qgdp[,3:5])
zt <- MTS::diffM(gdp)
# VAR(1)
m1 <- MTS::VAR(zt, p = 1)
## Constant term: 
## Estimates:  0.001713324 0.001182869 0.002785892 
## Std.Error:  0.0006790162 0.0007193106 0.0007877173 
## AR coefficient matrix 
## AR( 1 )-matrix 
##       [,1]  [,2]   [,3]
## [1,] 0.434 0.189 0.0373
## [2,] 0.185 0.245 0.3917
## [3,] 0.322 0.182 0.1674
## standard error 
##        [,1]   [,2]   [,3]
## [1,] 0.0811 0.0827 0.0872
## [2,] 0.0859 0.0877 0.0923
## [3,] 0.0940 0.0960 0.1011
##   
## Residuals cov-mtx: 
##              [,1]         [,2]         [,3]
## [1,] 2.893347e-05 1.965508e-06 6.619853e-06
## [2,] 1.965508e-06 3.246932e-05 1.686272e-05
## [3,] 6.619853e-06 1.686272e-05 3.893867e-05
##   
## det(SSE) =  2.721916e-14 
## AIC =  -31.09086 
## BIC =  -30.88722 
## HQ  =  -31.00813
# VAR(1) estacionário?
eigen(m1$Phi)$values
## [1] 0.70910488 0.08735388 0.05004080
# previsão 4 passos à frente
MTS::VARpred(m1, 4)
## orig  125 
## Forecasts at origin:  125 
##            uk       ca       us
## [1,] 0.002301 0.002467 0.003630
## [2,] 0.003314 0.003634 0.004582
## [3,] 0.004010 0.004480 0.005280
## [4,] 0.004498 0.005089 0.005774
## Standard Errors of predictions:  
##          [,1]     [,2]     [,3]
## [1,] 0.005379 0.005698 0.006240
## [2,] 0.006031 0.006764 0.006787
## [3,] 0.006309 0.007159 0.007043
## [4,] 0.006444 0.007346 0.007168
## Root mean square errors of predictions:  
##          [,1]     [,2]     [,3]
## [1,] 0.005464 0.005789 0.006339
## [2,] 0.040704 0.054184 0.039966
## [3,] 0.028021 0.035325 0.028630
## [4,] 0.020427 0.025433 0.020945
# VAR(2)
m2 <- MTS::VAR(zt, p = 2)
## Constant term: 
## Estimates:  0.001258163 0.001231581 0.002895581 
## Std.Error:  0.0007266338 0.0007382941 0.000816888 
## AR coefficient matrix 
## AR( 1 )-matrix 
##       [,1]  [,2]   [,3]
## [1,] 0.393 0.103 0.0521
## [2,] 0.351 0.338 0.4691
## [3,] 0.491 0.240 0.2356
## standard error 
##        [,1]   [,2]   [,3]
## [1,] 0.0934 0.0984 0.0911
## [2,] 0.0949 0.1000 0.0926
## [3,] 0.1050 0.1106 0.1024
## AR( 2 )-matrix 
##         [,1]   [,2]     [,3]
## [1,]  0.0566  0.106  0.01889
## [2,] -0.1914 -0.175 -0.00868
## [3,] -0.3120 -0.131  0.08531
## standard error 
##        [,1]   [,2]   [,3]
## [1,] 0.0924 0.0876 0.0938
## [2,] 0.0939 0.0890 0.0953
## [3,] 0.1038 0.0984 0.1055
##   
## Residuals cov-mtx: 
##              [,1]         [,2]         [,3]
## [1,] 2.824442e-05 2.654091e-06 7.435286e-06
## [2,] 2.654091e-06 2.915817e-05 1.394879e-05
## [3,] 7.435286e-06 1.394879e-05 3.569657e-05
##   
## det(SSE) =  2.258974e-14 
## AIC =  -31.13328 
## BIC =  -30.726 
## HQ  =  -30.96783
# VAR(2) estacionário?

# previsão 4 passos à frente
MTS::VARpred(m2, 4)
## orig  125 
## Forecasts at origin:  125 
##            uk        ca       us
## [1,] 0.003129 0.0005166 0.001660
## [2,] 0.002647 0.0031687 0.004889
## [3,] 0.003143 0.0048231 0.005205
## [4,] 0.003839 0.0053053 0.005998
## Standard Errors of predictions:  
##          [,1]     [,2]     [,3]
## [1,] 0.005315 0.005400 0.005975
## [2,] 0.005804 0.007165 0.007077
## [3,] 0.006202 0.007672 0.007345
## [4,] 0.006484 0.007785 0.007442
## Root mean square errors of predictions:  
##          [,1]     [,2]    [,3]
## [1,] 0.005461 0.005549 0.00614
## [2,] 0.038967 0.078131 0.06305
## [3,] 0.036637 0.045956 0.03329
## [4,] 0.031926 0.023140 0.02120

11.15.4 VARMA

Conforme (Tsay 2014, 127), a série temporal multivariada \(\boldsymbol{z}_{t}\) é um vetor autorregressivo de média móveis VARMA\((p,q)\), se \[\begin{equation} \boldsymbol{\phi}(B)\boldsymbol{z}_{t} = \boldsymbol{\phi}_0 + \boldsymbol{\theta}(B) \boldsymbol{a}_{t} \tag{11.61} \end{equation}\] onde \[\begin{equation} \boldsymbol{\theta}(B) = \boldsymbol{I}_k - \sum_{i=1}^{q} \boldsymbol{\theta}_i B^i \tag{11.62} \end{equation}\]

Sobre identificabilidade: veja (Tsay 2014, 127).

If the fitted VARMA model is adequate, the residual series \(\{\hat{a}_t\}\) should behave as a \(k\)-dimensional white noises. Thus, we continue to apply the multivariate Ljung–Box statistics (or Portmanteau statistic) (…) to check the serial and cross-correlations of the residuals. (Tsay 2014, 163)

Exemplo 11.70 Baseado nas documentações de MTS::VARMA() e MTS::VARMApred().

phi <- matrix(c(0.2,-0.6,0.3,1.1),2,2)
theta <- matrix(c(-0.5,0,0,-0.5),2,2)
sigma <- diag(2)
m1 <- VARMAsim(300, arlags = c(1), malags = c(1), 
               phi = phi, theta = theta, sigma = sigma)
zt <- m1$series
m2 <- MTS::VARMA(zt, p=1, q=1, include.mean = FALSE)
## Number of parameters:  8 
## initial estimates:  0.1619 0.3159 -0.7074 1.1276 0.5111 0.0431 0.2171 0.4939 
## Par. lower-bounds:  0.0455 0.2668 -0.8292 1.0763 0.3447 -0.0791 0.0431 0.366 
## Par. upper-bounds:  0.2783 0.365 -0.5856 1.1789 0.6775 0.1654 0.3912 0.6219 
## Final   Estimates:  0.1348409 0.3197087 -0.6750053 1.122453 0.5456 0.04958296 0.1749889 0.4531633 
## 
## Coefficient(s):
##       Estimate  Std. Error  t value Pr(>|t|)    
## [1,]   0.13484     0.07097    1.900   0.0574 .  
## [2,]   0.31971     0.03126   10.227  < 2e-16 ***
## [3,]  -0.67501     0.07771   -8.686  < 2e-16 ***
## [4,]   1.12245     0.03328   33.724  < 2e-16 ***
## [5,]   0.54560     0.06889    7.920 2.44e-15 ***
## [6,]   0.04958     0.04746    1.045   0.2962    
## [7,]   0.17499     0.08016    2.183   0.0290 *  
## [8,]   0.45316     0.05248    8.634  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --- 
## Estimates in matrix form: 
## AR coefficient matrix 
## AR( 1 )-matrix 
##        [,1] [,2]
## [1,]  0.135 0.32
## [2,] -0.675 1.12
## MA coefficient matrix 
## MA( 1 )-matrix 
##        [,1]    [,2]
## [1,] -0.546 -0.0496
## [2,] -0.175 -0.4532
##   
## Residuals cov-matrix: 
##            [,1]       [,2]
## [1,] 0.96366827 0.03345517
## [2,] 0.03345517 1.08112632
## ---- 
## aic=  0.09325368 
## bic=  0.1920212
MTS::VARMApred(m2, 4)
## Predictions at origin  300 
##         [,1]   [,2]
## [1,] 0.10283 0.2198
## [2,] 0.08414 0.1773
## [3,] 0.06804 0.1422
## [4,] 0.05465 0.1137
## Standard errors of predictions 
##        [,1]  [,2]
## [1,] 0.9817 1.040
## [2,] 1.2546 1.988
## [3,] 1.3811 2.711
## [4,] 1.5306 3.215

11.15.5 VARX

The first approach to include exogenous variables in multivariate time series modeling is to use the vector autoregressive model with exogenous variables. In the literature, this type of models is referred to as the VARX models with X signifying exogenous variables. (Tsay 2014, 346)

Seguindo (Tsay 2014, 346), a forma geral do modelo VARX é \[\begin{equation} \boldsymbol{z}_t = \boldsymbol{\phi}_0 + \sum_{i=1}^{p} \boldsymbol{\phi}_i \boldsymbol{z}_{t-i} + \sum_{j=1}^{s} \boldsymbol{\beta}_j \boldsymbol{x}_{t-j} + \boldsymbol{a}_t \tag{11.63} \end{equation}\]

Exemplo 11.71 Baseado no Exemplo 6.2 de (Tsay 2014, 346–50).

References

Diggle, Peter J. 1990. Time Series: A Biostatistical Introduction. Oxford University Press. https://academic.oup.com/book/53018.
Granger, Clive WJ. 1969. “Investigating Causal Relations by Econometric Models and Cross-Spectral Methods.” Econometrica: Journal of the Econometric Society, 424–38. https://www.jstor.org/stable/1912791.
Thurman, Walter N, Mark E Fisher, et al. 1988. “Chickens, Eggs, and Causality, or Which Came First.” American Journal of Agricultural Economics 70 (2): 237–38. http://sungpark.net/ChickensEggs.pdf.
Tsay, Ruey S. 2014. Multivariate time series analysis: with R and financial applications. John Wiley & Sons. http://past.rinfinance.com/agenda/2013/talk/RueyTsay.pdf.
Tsay, Ruey S., David Wood, and Jon Lachmann. 2022. MTS: All-Purpose Toolkit for Analyzing Multivariate Time Series (MTS) and Estimating Multivariate Volatility Models. https://CRAN.R-project.org/package=MTS.
Zeileis, Achim, and Torsten Hothorn. 2002. “Diagnostic Checking in Regression Relationships.” R News 2 (3): 7–10. https://CRAN.R-project.org/doc/Rnews/.